机器学习 学习笔记（持续更新）

机器学习 学习笔记

---

一、导论

1.1 什么是机器学习？

  机器学习是在没有明确设置的情况下使计算机具有学习能力的研究领域。(Arthur Samuel - 1959)
  计算机程序从经验E（计算机自己与自己下成千上百万次棋）中学习，解决某一任务T（下跳棋），进行某一性能度量P（与新对手玩跳棋时赢的概率），通过P测定在T上的表现因经验E而提高的程度。(Tom Mitchell - 1998)
  机器学习算法最主要分为监督学习（教会计算机某件事）和无监督学习（让计算机自己学会某件事）。

1.2 监督学习 Supervised learning

  监督学习是指我们给算法一个数据集，其中包含所有的已知量，即“正确答案”，之后计算机通过已知量去预测未知量，即得到更多的“正确答案”。
  监督学习也被称为回归问题，即通过离散数据预测连续的数值输出（例：通过房子的确切市场价格预测将要卖出的房子价格）。适用于监督学习算法的另一类问题即为分类问题，即通过多个特征、属性、线索来对数据集中的数据进行分类（例：预测肿瘤是良性的还是恶性的）。
  对于某些学习问题，我们希望通过不仅仅三五个特征来进行预测，而是通过无穷多的特征、属性、线索来进行预测。问题的关键在于如何处理这无穷多的特征，即如何在计算机中储存无穷多数量的事物（计算机内存会溢出）。

1.3 无监督学习 Unsupervised learning

  无监督学习是指算法得到的数据集中没有已知量（算法没有得到“正确答案”），数据的属性未知，数据的作用也未知，无监督学习算法尝试从数据集中寻找某种结构以解决问题。（聚类算法）
聚类算法被用于大型计算机群、社交网络分析、市场客户细分、天文数据分析等邻域。
  另一个无监督学习算法著名的例子是“鸡尾酒酒会”算法，即从多个声音叠加产生的音源中提取出原来的由单个个体产生的声音。可用于歌曲伴奏和人声的提取等领域。

---

二、第一个机器学习模型——线性回归模型

2.1 线性回归模型

  线性回归模型可能是世界上使用最广泛的机器学习算法。在熟悉了线性回归模型之后，其中的许多概念也适用于其他模型。
  回归模型中的回归意为该模型预测数字作为输出。任何预测数字的监督学习模型都是在解决所谓的回归问题。线性回归模型是回归模型的一个例子，在回归问题中，还有其他的解决模型。
  训练集：用来训练的数据集模型。以预测房价问题为例，以下就是一个训练集：

	输入变量（特征） $x$	输出变量（目标） $y$
编号	房子的面积（$f{t}^2$）	房子的价格（$）
1	2104	400
2	1416	232
3	1534	315
4	852	178
…	…	…
47	3210	870

  训练集的表示有其标准的符号。$m$代表训练实例的总数，$x$代表输入变量（输入的特征），$y$代表输出的变量（输出特征），($x^{(i)}$, $y^{(i)}$) 表示单个训练实例，上标$(i)$表示第几个训练实例。
  训练集中包括输入变量（Input features）和输出变量（Output targets），我们将训练集、输入变量和输出变量提供给学习算法。之后算法会产生一个方法，用 $f$ 表示，这是一个函数。通过这个方法 $f$ ，我们可以根据输入变量得到算法对这个输入特征的预测值。预测值用 $\hat{y}$ 表示， 实际值用 $y$ 表示。
  对于上述的回归问题，我们坚持用直线进行拟合。$f$ 函数可以用以下方法表示，且下两种表示方法完全等价。
$$\begin{gathered} f_{w,b}(x)=wx+b \\ f(x)=wx+b \end{gathered}$$
  这个特殊的模型就称为线性回归模型，并且它是一个单个输入变量或特征x的模型，称为单变量线性回归模型（Univariate linear regression）。

2.2 代价函数 Cost function

  要实现线性回归，关键的第一步是定义代价函数。代价函数会告诉我们模型做的有多好，这样我们就可以试着让他做的更好。在 $f$ 函数中的 $w$ 和 $b$ 称为模型的参数，模型的参数是你可以在训练中调整的变量，以改进模型。有时候将 $w$ 和 $b$ 称为模型的系数或者权重。
  对于算法建立的模型，$w$ 和 $b$ 确定出一条直线。通过这条直线，我们可以得到 $\hat{y}$，即模型对于 $x$ 的预测值。我们将 $\hat{y}$ 减去 $y$ 的值称为误差（error）。要找到 $w$ 和 $b$ 使其更好的拟合于模型，对于所有的训练实例，我们要减小误差。
  下面的函数称为平方误差代价函数：
$$\begin{gathered} J(w,b)=\frac{1}{2m}\sum _{i=1}^m({\hat{y}}^{(i)}-y^{(i)}{)}^2 \\ J(w,b)=\frac{1}{2m}\sum _{i=1}^m(f_{w,b}(x^{(i)})-y^{(i)}{)}^2 \end{gathered}$$
  以上是代价函数的数学定义，接下来对代价函数的实际作用建立一些直观理解。代价函数J的作用是衡量模型的预测值于y的真实值之间的差异。我们的目标是通过调整 $w$ 和 $b$ 的值，使 $J$ 缩小。这里采用一个简化模型（使 $b=0$），以便直观理解。
$$\begin{gathered} f_w(x)=wx \\ J(w)=\frac{1}{2m}\sum _{i=1}^m(f_w(x^{(i)})-y^{(i)}{)}^2 \end{gathered}$$
  下面这张图描绘了如何找到 $J(w)$ 的最小值。对于不同的 $w$，根据左边的 $f(x)$ 我们能得到多个 $J(w)$，从而能够绘制出 $J(w)$的图像。可以看到，当 $w=1$ 时我们得到了 $J(w)$ 的最小值。

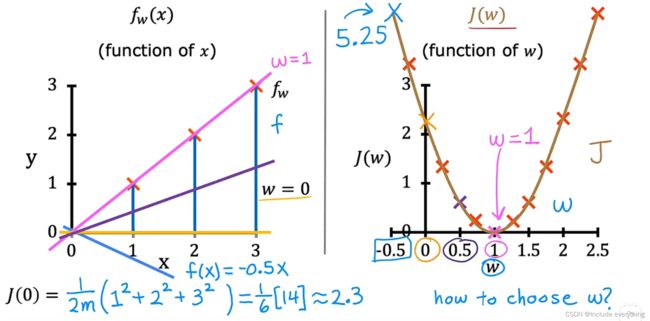
  上图是一个简化的模型，$J(w)$ 只有一个参数 $w$ ，我们得到一个二维图像。依次类推，通过调整不同的 $w$ 和 $b$ ，我们可以得到 $J(w,b)$ 的三维图像，从而得到 $J$ 的最小值。需要强调的是，这个曲面上的任何一个点都代表w和b的某些特定选择。

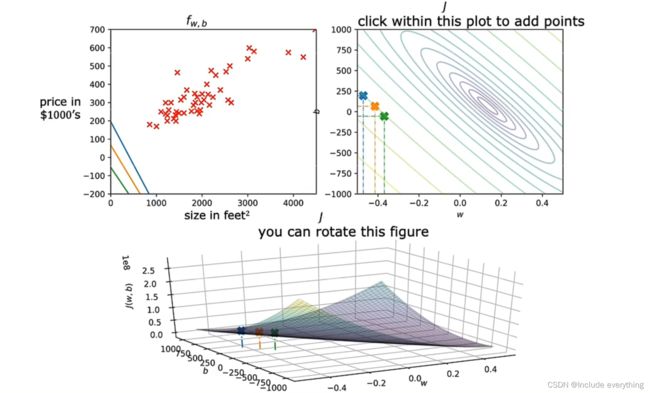
  对于下面的图，我们用类似等高地形图的概念来描绘这个曲面。下图中右上角的图中的每一个椭圆代表曲面上的点（对于特定的 $w$ 和 $b$ ）的 $J(w,b)$ 值相同，即它们 “高度相同” 。

2.3 梯度下降 Gradient descent

  上面一节讨论了模型的参数和代价函数之间的关系。但是要想找到 $J$ 的最小值，我们不希望通过手动选择的方式。我们需要程序可以自动找到对于拟合数据最适合的参数，要实现这一点，我们需要使用梯度下降算法。该算法是机器学习中最重要的算法之一。梯度下降算法在机器学习中无处不在，梯度下降不仅用于训练线性回归，还可以用于人工智能中一些更大更复杂的模型。
  梯度下降算法可以用来找到任何函数的最小值，不仅仅是代价函数。对于线性回归模型，首先要做的是对 $w$ 和 $b$ 进行一些“初步猜测”，初始值最开始是多少并不重要，通常将它们都设置为 $0$。之后不断地改变 $w$ 和 $b$ ，直到有希望 $J$ 稳定在或接近于最小值。需要注意的是，对于某些函数，J可能不是弓形或碗形，有可能有不止一个可能的最小值。
  为了直观理解这一过程，同时理解梯度下降中的“梯度”的数学含义，下面是一个例子。如果你站在一座山的山顶（通过对 $w$ 和 $b$ 的值进行设置），环顾四周（计算沿各个方向的梯度），找到最陡的一条路（梯度最小的方向）迈出一小步，重复这个过程，最后总会找到一个山谷的谷底（函数的局部极小值）。需要注意的是，通过设置不同的参数初始值，可能会得到不同的局部极小值，并且得到一个局部的极小值之后无法再得到另一个。

  下面是梯度下降的数学表达式（对于 $w$ ）：
$$w^{\prime }=w-\alpha \frac{\partial }{\partial w}J(w,b),程序中写作w=w-\alpha \frac{\partial }{\partial w}J(w,b)$$
  左边的式子是数学表达，右边的式子是再程序中体现的数学表达式。式中的 $\alpha$ 称为学习率（学习速率），学习率通常是0到1之间的一个小正数，例如 $0.01$ 。$\alpha$ 的作用是控制你下坡时下坡的“步幅”，稍后将讨论如何选择一个合适的学习率。对于 $b$ 的梯度下降表达式与 $w$ 的十分相似：
$$b^{\prime }=b-\alpha \frac{\partial }{\partial b}J(w,b),程序中写作b=b-\alpha \frac{\partial }{\partial b}J(w,b)$$
  重复对 $w$ 和 $b$ 两步赋值操作，直到算法收敛：到达一个局部最小值，在这个最小值下，参数 $w$ 和 $b$ 不再随着你采取的每一个额外步骤而改变很多。
  编写程序时一个重要的细节是：在进行梯度下降时，我们希望同时改变 $w$ 和 $b$ 的值。即先计算 $J(w,b)$ 的两个偏微分，然后再改变 $w$ 和 $b$ 的值。
  下面讨论对学习率 $\alpha$ 的选择问题。$\alpha$ 的选择会对梯度下降的效率产生巨大的影响。如果学习速率太小，代表迈出的每一步都很小，运行梯度下降所需要的时间就会下降，降低了效率；如果学习速率太大，梯度下降可能会超调，可能永远不会达到最小，导致离最小值越来越远。但还存在另一种可能，即梯度下降可能无法收敛，甚至可能发散。
  在选取一个合适的学习率之后，当我们逐步接近最小值时，梯度下降的“步幅”会自动逐步缩小。原因是导数项会逐渐变小，但学习率不变。

2.4 实现线性回归的梯度下降算法

  首先来计算平方误差代价函数 $J(w,b)$对 $w$ 的偏导数（对 $b$ 的偏导数类似）：
$$\begin{gathered} \frac{\partial }{\partial w}J(w,b)=\frac{\partial }{\partial w}\frac{1}{2m}\sum _{i=1}^m(f_w(x^{(i)})-y^{(i)}{)}^2 \\ =\frac{\partial }{\partial w}\frac{1}{2m}\sum _{i=1}^m(w{x}^{(i)}+b-y^{(i)}{)}^2 \\ =\frac{1}{2m}\sum _{i=1}^m(w{x}^{(i)}+b-y^{(i)})2x^{(i)} \\ =\frac{1}{m}\sum _{i=1}^m(f_{w,b}(x^{(i)})-y^{(i)})x^{(i)} \\ \frac{\partial }{\partial b}J(w,b)=...=\frac{1}{m}\sum _{i=1}^m(f_{w,b}(x^{(i)})-y^{(i)}) \end{gathered}$$
  可以看出，平方误差代价函数前面系数 $1/2m$ 的分母上的 $2$ 是为了使求偏导后算式的形式更为整齐。
  对于普通的函数，对系数作不同的初始值设置可能会使梯度下降算法可能会找到函数的局部最小值。但对于平方误差代价函数是一个凹函数，其只有一个全局最小值。只要学习率选取适当，它总是能收敛到全局最小值。
  更精确地说，这种梯度下降称为间歇梯度下降。间歇指在梯度下降地每一个步骤上，我们使用了训练集中的所有训练实例，而不仅仅是训练数据的子集（计算导数时我们对所有训练实例的误差进行累加后求平均值）。

2.5 代码实现

  训练集数据如下（城市的人口和当地餐馆利益的关系）：

1.01,30.32
1.6,44
1.7,48
1.9,55
2.2,58.11
2.4,71.88
2.8,79.9
3.0,90.16
3.1,92.55
3.3,89.9
3.5,87.16
4.0,118.43
5.12,150.44

  训练集散点图如下所示：

  代码实现如下：

# 代码创建日期：2022/8/30 16:23
# 主要作用 单变量线性回归模型
import matplotlib.pyplot as plt

# 从txt文件中读取数据，绘制成散点图
f = open("data.txt", 'r')
# 读取数据
population = []
profit = []
for line in f.readlines():
    col1 = line.split(',')[0]
    col2 = line.split(',')[1].split('\n')[0]
    population.append(float(col1))
    profit.append(float(col2))

# 绘制图像
plt.title("Scatter plot of training data")
plt.xlabel("population of city")
plt.ylabel("profit")
plt.scatter(population, profit, marker='x')
plt.show()

m = len(population)  # m是训练集中训练实例的总数

# 代价函数J(w, b)的计算
J = 0
w = 0
b = 0
for i in range(m):
    # pow(x, y)返回x的y次方的值
    J += 1.0 / (2 * m) * pow(w * population[i] + b - profit[i], 2)

# 梯度下降
alpha = 0.01  # 设置学习速率
iterations = 1500  # 梯度下降的迭代轮数
w = 0
b = 0
t = []  # t是每次迭代的下标
cost = []   # 用cost列表记录每轮迭代J的变化
temp_J = 0
for i in range(iterations):
    temp_w = w
    temp_b = b
    for j in range(m):
        temp_w -= (alpha / m) * (w * population[j] + b - profit[j]) * population[j]
        temp_b -= (alpha / m) * (w * population[j] + b - profit[j])
    w = temp_w
    b = temp_b
    # 对每一轮的代价函数进行记录
    for k in range(m):
        temp_J += 1.0 / (2 * m) * pow(w * population[k] + b - profit[k], 2)
    cost.append(temp_J)
    t.append(i)
    temp_J = 0

# 绘制拟合出的直线
x = [1, 5]
y = [x[0] * w + b, x[1] * w + b]
plt.plot(x, y, color='red')
plt.title('Linear Regression')
plt.xlabel('population of city')
plt.ylabel('profit')
plt.scatter(population, profit, marker='x')
plt.show()

# 代价函数J的可视化
plt.title('Visualizing J(w, b)')
plt.xlabel('iterations')
plt.ylabel('cost')
plt.plot(t, cost, color='red')  # t是迭代轮数，cost是每轮的代价函数的值
plt.show()

  拟合出的直线如下图所示：

  通过代码绘制出的代价函数如下所示（可以看到，代价函数在迭代轮数很小的时候就稳定在了最小值附近）：

三、多元回归

3.1 多元线性回归 Multiple linear regression

  上一章讨论了单变量线性回归模型。但在更多的情况下，我们希望通过多个特征来预测结果，这时我们就要对训练集中的多个特征进行表示。下面是一个包含多个输入变量的训练集。

输入特征 $x_1$	输入特征 $x_2$	输入特征 $x_3$	输入特征 $x_4$	输出变量 $y$
房子的大小（$m^2$）	卧室数量（个）	房屋层数（层）	房龄（年）	价格（万元）
2104	5	1	45	460
1416	3	2	40	232
1534	3	2	30	315
834	2	1	36	178
…	…	…	…	…

  我们引入更多的符号来表示这个训练集中的信息。使用 $x_1$，$x_2$，$x_3$，$x_4...$来代表不同的特征，用简写 $x_j$ 来表示特征列表。
$$\begin{gathered} x_j\to 第j个特征 \\ n\to 特征的总数 \\ {x}^{(i)}\to 第i个训练实例 \\ {x}_j^{(i)}\to 第i个训练实例中的第j个特征值 \end{gathered}$$
  如图表所示，第 $i$ 个训练实例是由四个数字组成的列表，其组成了一个向量。$x$上面的箭头是一个可省略的符号，其意义只是强调这是所有输入变量中的一个向量。
  下面来定义对于多个特征的模型，对于上面的训练集可以这样定义：
$$f_{w,b}(x)=w_1{x}_1+w_2{x}_2+w_3{x}_3+w_4{x}_4+b$$
  对于下面这个特例：
$$f_{w,b}(x)=0.1x_1+4x_2+10x_3-2x_4+80$$
  输入特征前面的系数可以这样理解：房屋的最低价格为 $80$ 万元（假设房屋的各个输入特征均为$0$，$b=80$），房屋的价格每增加1平方米价格就增加 $0.1$ 万元（$w_1=0.1$），每增加一间卧室房屋价格增加 $4$ 万元（$w_2=4$），房屋每增加一层价格增加$10$万元（$w_3=10$），房屋的年龄每增加一年价格就下跌 $2$ 万元（$w_4=-2$）
  对于一般情况，具有多种特征的线性模型称为多元线性回归模型，可以有以下定义：
$$f_{w,b}(x)=w_1{x}_1+w_2{x}_2+w_3{x}_3+...+w_n{x}_n+b$$
  接下来引入一些符号用一种更简单但等价的方式重写这个表达式，w和x都变成行向量。
$$\begin{gathered} w=[w_1{w}_2{w}_3...w_n] \\ x=[x_1{x}_2{x}_3...x_n] \\ {f}_{w,b}(x)=w\cdot x+b \end{gathered}$$
  需要强调的是，上面的模型不是多元回归模型，其只局限于用直线来拟合数据的情况。

---

持续更新中……