(01)ORB-SLAM2源码无死角解析-(19) 重投影误差,卡方检验→CheckFundamental,CheckHomography

讲解关于slam一系列文章汇总链接:史上最全slam从零开始，针对于本栏目讲解的(01)ORB-SLAM2源码无死角解析链接如下(本文内容来自计算机视觉life ORB-SLAM2 课程课件):
(01)ORB-SLAM2源码无死角解析-(00)目录_最新无死角讲解：https://blog.csdn.net/weixin_43013761/article/details/123092196
 
$文末正下方中心提供了本人联系方式，点击本人照片即可显示WX\to 官方认证$
 

一、前言

先回顾一下前面的内容：

$(1):$ 主调函数为 FindHomography 函数，其内部核心函数为:

Normalize()  归一化操作
ComputeH21() 八点法计算参考帧到当前帧的H矩阵
CheckHomography() 重投影误差评分

$(2):$ 主调函数为 FindFundamental 函数，其内部核心函数为:

Normalize()  归一化操作
ComputeF21() 八点法计算计算F矩阵
CheckFundamental() 重投影误差评分

FindHomography 与 FindHomography 实现于 src/Initializer.cc 文件中，可以和明显看到其命名是十分相似的，其实他们的功能也是比较类似的。针对于 ComputeH21() 与 ComputeF21() 函数已经在上面讲解过了，通过其可以计算出 $\mathbf{H}$ 与 $\mathbf{F}$ 矩阵。那么计算出来的矩阵否者正常呢？

为了检验计计算出来的 $\mathbf{H}$ 与 $\mathbf{F}$ 矩阵 是否正常，分别使用了 CheckHomography() 与 CheckFundamental() 函数。因为他们的代码十分的类似，这里就以 CheckFundamental() 为例了。其主要分为两个部分，为重投影，误差评分。

根据前面的博客，在 FindHomography 与 FindFundamental 函数中，其会使用八点法求解 单应矩阵H 与 基本矩阵F，简单的说，就是随机选择4对(8个)关键点，根据匹配关系，进而求得 H 与 F 矩阵。但是这里很明显存在一个问题，那就是随机选择4对(8个)关键点求解的出来的 H 与 F 矩阵并不一定就是最好的，比如说，随机选择的4对点中，万一有一对属于异常匹配点呢？

所以源码中的做法是，每次随机选择4对(8个)关键点求解的出来的 H 与 F 矩阵，这样的操作执行了 mMaxIterations=200 次，然后从这 mMaxIterations 次中，选出最好的结果，作为最终的结果。那么下面就来看看其是如何选择最好的一个的。当然，在这之前大家需要了解卡方检验得相关知识，如果不太了解可以看一下这篇博客，史上最简SLAM零基础解读(6) - 卡方分布(chi-square distribution)和()卡方检验(Chi-Squared Test) → 理论讲解与推导

 

二、代码流程与注释

代码位于src/Initializer.cc 的 float Initializer::CheckHomography() 函数中

$步骤1:$ 对当前帧与参考帧匹配上得特征点对进行遍历。对应代码如下：

const int N = mvMatches12.size();
    for(int i = 0; i < N; i++)

 
$步骤2:$ 将当前帧特征点通过单应变换投影到参考帧中，对应代码如下：

        const float w2in1inv = 1.0/(h31inv * u2 + h32inv * v2 + h33inv);
        const float u2in1 = (h11inv * u2 + h12inv * v2 + h13inv) * w2in1inv;
        const float v2in1 = (h21inv * u2 + h22inv * v2 + h23inv) * w2in1inv;

 
$步骤3:$ 计算重投影误差，主要是计算投影点与对应匹配点的像素距离的平方，作为卡方值，对应代码如下：

        // 计算重投影误差 = ||p1(i) - H12 * p2(i)||2
        const float squareDist1 = (u1 - u2in1) * (u1 - u2in1) + (v1 - v2in1) * (v1 - v2in1);
        const float chiSquare1 = squareDist1 * invSigmaSquare;

 
$步骤4:$ 与卡方检验的临界值进行对比，自由度为2的卡方分布，显著性水平为0.05，对应的临界阈值th = 5.991，根据结果同时标记该点是否为内点，对应代码如下：

        // 用阈值标记离群点，内点的话累加得分
        if(chiSquare2>th)
            bIn = false;
        else
            score += th - chiSquare2;   

        // Step 2.4 如果从img2 到 img1 和 从img1 到img2的重投影误差均满足要求，则说明是Inlier point
        if(bIn)
            vbMatchesInliers[i]=true;
        else
            vbMatchesInliers[i]=false;

 
$注意:$ 在步骤3中，计算卡方的时候乘以了一个 invSigmaSquare，另外就是为什么自由度为2，下面会对其进行详细讲解，在这之前，我先把 CheckHomography 函数的注释贴一下：

/**
 * @brief 对给定的homography matrix打分,需要使用到卡方检验的知识
 * 
 * @param[in] H21                       从参考帧到当前帧的单应矩阵
 * @param[in] H12                       从当前帧到参考帧的单应矩阵
 * @param[in] vbMatchesInliers          匹配好的特征点对的Inliers标记
 * @param[in] sigma                     方差，默认为1
 * @return float                        返回得分
 */
float Initializer::CheckHomography(
    const cv::Mat &H21,                 //从参考帧到当前帧的单应矩阵
    const cv::Mat &H12,                 //从当前帧到参考帧的单应矩阵
    vector<bool> &vbMatchesInliers,     //匹配好的特征点对的Inliers标记
    float sigma)                        //估计误差
{
    // 说明：在已值n维观测数据误差服从N(0，sigma）的高斯分布时
    // 其误差加权最小二乘结果为  sum_error = SUM(e(i)^T * Q^(-1) * e(i))
    // 其中：e(i) = [e_x,e_y,...]^T, Q维观测数据协方差矩阵，即sigma * sigma组成的协方差矩阵
    // 误差加权最小二次结果越小，说明观测数据精度越高
    // 那么，score = SUM((th - e(i)^T * Q^(-1) * e(i)))的分数就越高
    // 算法目标： 检查单应变换矩阵
    // 检查方式：通过H矩阵，进行参考帧和当前帧之间的双向投影，并计算起加权最小二乘投影误差

    // 算法流程
    // input: 单应性矩阵 H21, H12, 匹配点集 mvKeys1
    //    do:
    //        for p1(i), p2(i) in mvKeys:
    //           error_i1 = ||p2(i) - H21 * p1(i)||2
    //           error_i2 = ||p1(i) - H12 * p2(i)||2
    //           
    //           w1 = 1 / sigma / sigma
    //           w2 = 1 / sigma / sigma
    // 
    //           if error1 < th
    //              score +=   th - error_i1 * w1
    //           if error2 < th
    //              score +=   th - error_i2 * w2
    // 
    //           if error_1i > th or error_2i > th
    //              p1(i), p2(i) are inner points
    //              vbMatchesInliers(i) = true
    //           else 
    //              p1(i), p2(i) are outliers
    //              vbMatchesInliers(i) = false
    //           end
    //        end
    //   output: score, inliers

	// 特点匹配个数
    const int N = mvMatches12.size();

	// Step 1 获取从参考帧到当前帧的单应矩阵的各个元素
    const float h11 = H21.at<float>(0,0);
    const float h12 = H21.at<float>(0,1);
    const float h13 = H21.at<float>(0,2);
    const float h21 = H21.at<float>(1,0);
    const float h22 = H21.at<float>(1,1);
    const float h23 = H21.at<float>(1,2);
    const float h31 = H21.at<float>(2,0);
    const float h32 = H21.at<float>(2,1);
    const float h33 = H21.at<float>(2,2);

	// 获取从当前帧到参考帧的单应矩阵的各个元素
    const float h11inv = H12.at<float>(0,0);
    const float h12inv = H12.at<float>(0,1);
    const float h13inv = H12.at<float>(0,2);
    const float h21inv = H12.at<float>(1,0);
    const float h22inv = H12.at<float>(1,1);
    const float h23inv = H12.at<float>(1,2);
    const float h31inv = H12.at<float>(2,0);
    const float h32inv = H12.at<float>(2,1);
    const float h33inv = H12.at<float>(2,2);

	// 给特征点对的Inliers标记预分配空间
    vbMatchesInliers.resize(N);

	// 初始化score值
    float score = 0;

    // 基于卡方检验计算出的阈值（假设测量有一个像素的偏差）
	// 自由度为2的卡方分布，显著性水平为0.05，对应的临界阈值
    const float th = 5.991;

    //信息矩阵，方差平方的倒数
    const float invSigmaSquare = 1.0/(sigma * sigma);

    // Step 2 通过H矩阵，进行参考帧和当前帧之间的双向投影，并计算起加权重投影误差
    // H21 表示从img1 到 img2的变换矩阵
    // H12 表示从img2 到 img1的变换矩阵 
    for(int i = 0; i < N; i++)
    {
		// 一开始都默认为Inlier
        bool bIn = true;

		// Step 2.1 提取参考帧和当前帧之间的特征匹配点对
        const cv::KeyPoint &kp1 = mvKeys1[mvMatches12[i].first];
        const cv::KeyPoint &kp2 = mvKeys2[mvMatches12[i].second];
        const float u1 = kp1.pt.x;
        const float v1 = kp1.pt.y;
        const float u2 = kp2.pt.x;
        const float v2 = kp2.pt.y;

        // Step 2.2 计算 img2 到 img1 的重投影误差
        // x1 = H12*x2
        // 将图像2中的特征点通过单应变换投影到图像1中
        // |u1|   |h11inv h12inv h13inv||u2|   |u2in1|
        // |v1| = |h21inv h22inv h23inv||v2| = |v2in1| * w2in1inv
        // |1 |   |h31inv h32inv h33inv||1 |   |  1  |
		// 计算投影归一化坐标
        const float w2in1inv = 1.0/(h31inv * u2 + h32inv * v2 + h33inv);
        const float u2in1 = (h11inv * u2 + h12inv * v2 + h13inv) * w2in1inv;
        const float v2in1 = (h21inv * u2 + h22inv * v2 + h23inv) * w2in1inv;
   
        // 计算重投影误差 = ||p1(i) - H12 * p2(i)||2
        const float squareDist1 = (u1 - u2in1) * (u1 - u2in1) + (v1 - v2in1) * (v1 - v2in1);
        const float chiSquare1 = squareDist1 * invSigmaSquare;

        // Step 2.3 用阈值标记离群点，内点的话累加得分
        if(chiSquare1>th)
            bIn = false;    
        else
            // 误差越大，得分越低
            score += th - chiSquare1;

        // 计算从img1 到 img2 的投影变换误差
        // x1in2 = H21*x1
        // 将图像2中的特征点通过单应变换投影到图像1中
        // |u2|   |h11 h12 h13||u1|   |u1in2|
        // |v2| = |h21 h22 h23||v1| = |v1in2| * w1in2inv
        // |1 |   |h31 h32 h33||1 |   |  1  |
		// 计算投影归一化坐标
        const float w1in2inv = 1.0/(h31*u1+h32*v1+h33);
        const float u1in2 = (h11*u1+h12*v1+h13)*w1in2inv;
        const float v1in2 = (h21*u1+h22*v1+h23)*w1in2inv;

        // 计算重投影误差 
        const float squareDist2 = (u2-u1in2)*(u2-u1in2)+(v2-v1in2)*(v2-v1in2);
        const float chiSquare2 = squareDist2*invSigmaSquare;
 
        // 用阈值标记离群点，内点的话累加得分
        if(chiSquare2>th)
            bIn = false;
        else
            score += th - chiSquare2;   

        // Step 2.4 如果从img2 到 img1 和 从img1 到img2的重投影误差均满足要求，则说明是Inlier point
        if(bIn)
            vbMatchesInliers[i]=true;
        else
            vbMatchesInliers[i]=false;
    }
    return score;
}

 

三、细节疑点分析

$疑点1：$在计算卡方的时候，是使用距离的平方，然后再乘了一个invSigmaSquare，该值其实是可以忽略的，因为在初始化的时候，代码为 new Initializer(mCurrentFrame,1.0,200)，也就是说 invSigmaSquare 的值为1，其作用可能是用来调整恒定误差的。

$疑点2：$ 自由度为二，不是很明白的同学可以先阅读一下这篇文章→用可视化思维解读统计自由度，简单的说，自由度就是在一定限制之下(或者没有限制)的情况下，可以任意取值变量的个数，我们再来看步骤的源码:

const float squareDist1 = (u1 - u2in1) * (u1 - u2in1) + (v1 - v2in1) * (v1 - v2in1)，

其上我可以任意取值的变量有两个，分别为为 u2in1与 u2in1。这里是没有限制的(比如两者只和为固定数值)，所以其自由度为2。也就是2维坐标。再后面的过程中，如果使用的是深度摄像头，可以发现其在进行卡方检验的时候，自由度为3，因为这个时候又多了一个维度出来。

$疑点3：$ 在使用卡方检验的时候，需要有一个前提，那就是正态分布的独立变量才能使用卡方检验，那么证明证明重投影误差是符合正太分布的呢？

正态分布（Normal distribution）又名高斯分布（Gaussian distribution），是一个在数学、物理及工程等领域都非常重要的概率分布，在统计学的许多方面有着重大的影响力。若随机变量X服从一个数学期望为 $\mu$、方差为 $\sigma$ 的高斯分布，记为$N\left(\mu ,{\sigma }^{\wedge }2\right)$。如下图所示：

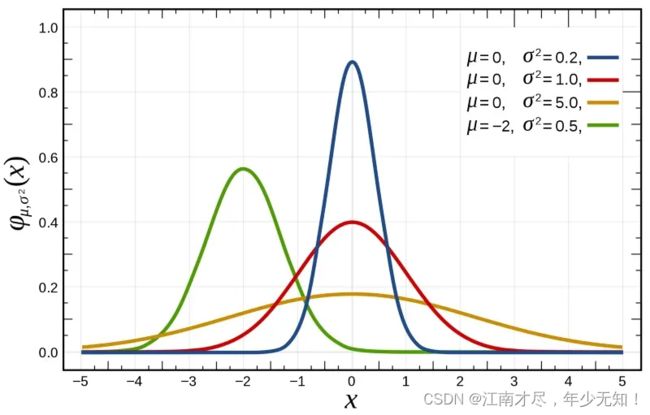
可以看到 $\mu$ 表示期望控制高峰值，方差为 $\sigma$ 控制分布方式。很明显， 对于重投影误差来说，我们期望肯定是0，因为重投影误差为0的时候效果是最好的。记 $\mathbf{u}$ 为特征点的2D位置，$\overline{\mathbf{u}}$ 为由地图点投影到图像上的2D位置。重投影误差为:$$\mathbf{e}=\mathbf{u}-\overline{\mathbf{u}}\text{\hspace{1em}(01)}$$重投影误差服从高斯分布$$\mathbf{e}\sim N(0,\mathbf{\Sigma })\text{\hspace{1em}(02)}$$
其中，协方差 $\mathbf{\Sigma }$ 一般根据特征点提取的金字塔层级确定。具体的，记提取ORB特征时，图像金字塔的每层缩小尺度为 (ORB-SLAM中为1.2)。在ORB-SLAM中假设第0层的标准差为 $p$ 个pixel (ORB-SLAM中设为了1个pixel)；那么，一个在金字塔第 $\mathbf{n}$ 层提取的特征的重投影误差的协方差为
$$\mathbf{\Sigma }={\left(s^n\times p\right)}^2\left[\begin{array}{ll}1& 0\\ & \\ 0& 1\end{array}\right]\text{\hspace{1em}(03)}$$回头再看一下式(1)中的误差是一个2维向量，阈值也不好设置吧。那就把它变成一个标量，计算向量的内积 $\mathbf{r}$(向量元素的平方和)。但是，这又有一个问题，不同金字塔层的特征点都用同一个阈值，是不是不合理呢。于是，在计算内积的时候，利用协方差进行加权（协方差表达了不确定度）。金字塔层级越高，特征点提取精度越低，协方差 越大，那么就有了
$$\mathbf{r}={\mathbf{e}}^T{\mathbf{\Sigma }}^{-1}\mathbf{e}\text{\hspace{1em}(04)}$$利用协方差加权，起到了归一化的作用。具体的(4)式，可以变为$$\mathbf{r}={\left({\mathbf{\Sigma }}^{-\frac{1}{2}}\mathbf{e}\right)}^T\left({\mathbf{\Sigma }}^{-\frac{1}{2}}\mathbf{e}\right)\text{\hspace{1em}(05)}$$为多维标准正态分布，也就是说不同金字塔层提取的特征，计算的重投影误差都被归一化了，或者说去量纲化了，那么，我们只用一个阈值就可以了。可见，金字塔层数越高，图像分辨率越低，特征提取的精度也就越低，因此协方差越大。
 

四、结语

通过该篇博客，对重投影误差以及卡方检验进行了一个详细的讲解，在后面过程中，这两个内容我们依旧会经常使用到。
 
 
本文内容来自计算机视觉life ORB-SLAM2 课程课件