ORBSLAM中的卡方检验

ORB2单目读代码笔记13--卡方检验原理及其在ORB-SLAM2中的用处_不能再吃了OvO的博客-CSDN博客_orbslam 卡方检验

 

 卡方检验详解分析与实例_bitcarmanlee的博客-CSDN博客_卡方检验例题与解析

 

 cvlife

3.2 卡方检验

为什么要引用卡方检验?

以特定概率分布为某种情况建模时，事物长期结果较为稳定，能够清晰进行把握。比如抛硬币实验。

但是期望与事实存在差异怎么办？偏差是正常的小幅度波动？还是建模错误？此时，利用卡方分布 分析结果 ，排除 可疑结果 。

简单来说：当事实与期望不符合情况下使用卡方分布进行检验，看是否系统出了问题，还是属于正常波动

Version:0.9 StartHTML:0000000105 EndHTML:0000004169 StartFragment:0000000141 EndFragment:0000004129

卡方分布用途？

检查实际结果与期望结果之间何时存在显著差异。

1、检验拟合程度：也就是说可以检验一组给定数据与指定分布的吻合程度。如：用它检验抽奖机收益的观察频数与我们所期望的吻合程

度。

2、检验两个变量的独立性：通过这个方法检查变量之间是否存在某种关系。

卡方分布假设检验步骤？

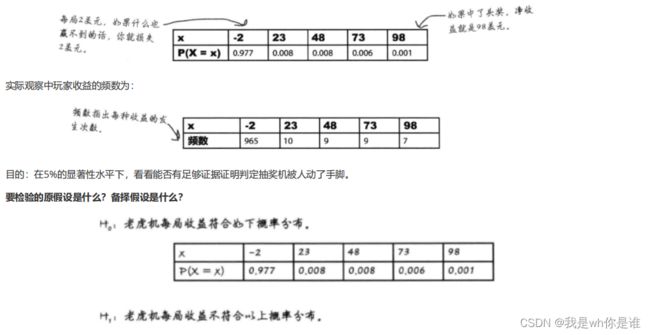
1、确定要进行检验的假设（H0）及其备择假设H1.

2、求出期望E.

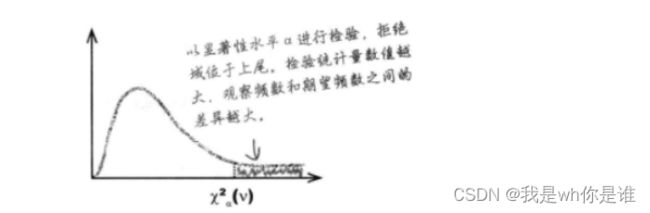
3、确定用于做决策的拒绝域（右尾）.

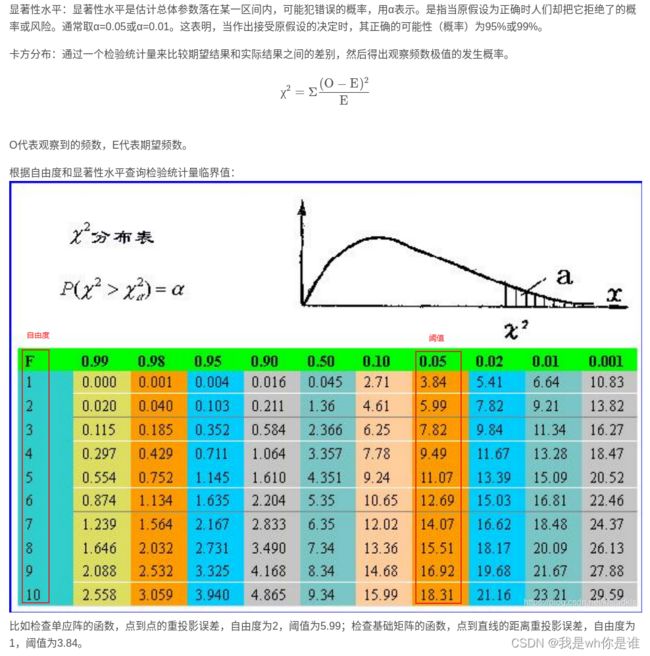
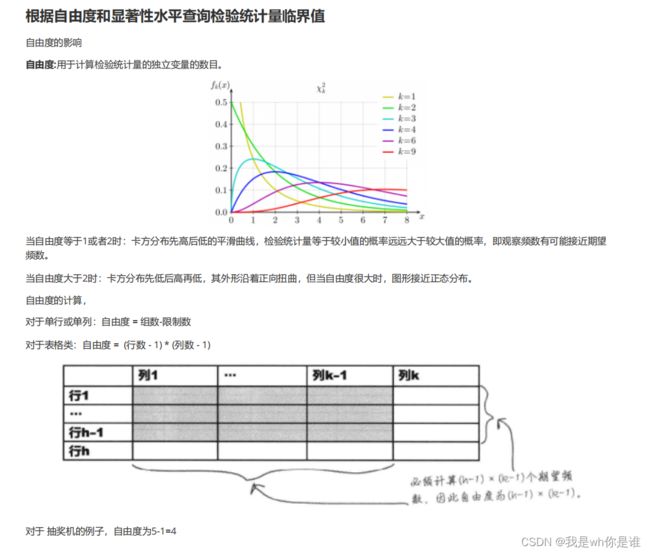
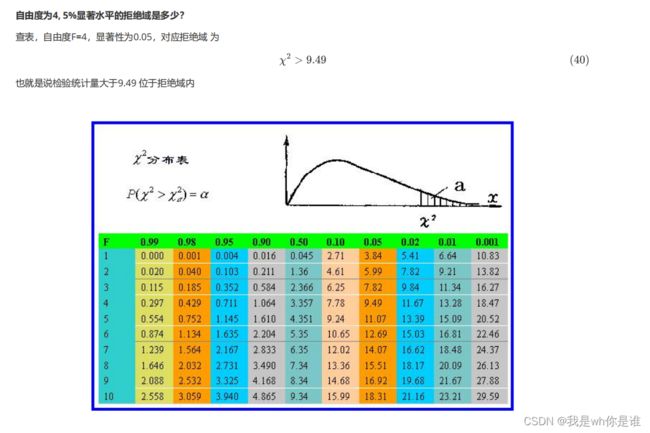
4、根据 自由度 和 显著性水平 查询检验统计量临界值.

5、查看检验统计量是否在拒绝域内.

6、做出决策.

一个例子：抽奖机之谜

抽奖机，肯定都不陌生，现在一些商场超市门口都有放置。正常情况下出奖概率是一定的，综合来看，商家收益肯定大于支出。

倘若突然某段时间内总是出奖，甚是反常，那么到底是某阶段是小概率事件还是有人进行操作了？ 抽奖机怎么了？ 针对这种现象或者类似这

种现象问题则可以借助卡方进行检验，暂且不着急如何检验，还是补充一下基础知识，再逐步深入解决问题。【常规事件中出现非常规现

象，如何检查问题所在的情况下使用卡方分布】

下面是某台抽奖机的期望分布，其中X代表每局游戏的净收益（每局独立事件）：

什么是显著性水平？

显著性水平是估计总体参数落在某一区间内，可能犯错误的概率，用α表示。

显著性水平是 假设检验 中的一个概念，是指当原假设为正确时人们却把它拒绝了的概率或风险。它是公认的小概率事件的概率值，必须在每

一次统计检验之前确定，通常取 α=0.05或α=0.01 。这表明，当作出接受原假设的决定时，其 正确的可能性（概率）为95%或99% 。

卡方分布指出观察频数与期望频数之间差异显著性，和其他假设一样，这取决于显著性水平。

1、显性水平α进行检验，则写作：（常用的显著性水平1%和5%）

2、检测标准：卡方分布检验是单尾检验且是右尾，右尾被作为 拒绝域 。于是通过查看检验统计量是否位于右尾的拒绝域以内，来判定期望

分布得出结果的可能性。

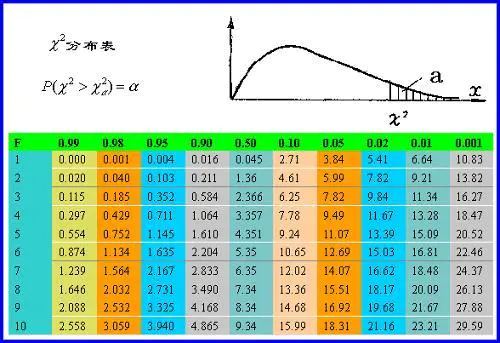
3、卡方概率表的使用：卡方临界值表是给定可以查询的

问题简述

抽奖机平常收益者总是商家，突然一段时间总是出奖。本来小概率事件频发，我们利用卡方的检验拟合优度看看能否有足够证据证明判定抽

奖机被人动了手脚 卡方分布是什么？

通过一个检验统计量来比较 期望结果 和 实际结果 之间的差别，然后得出观察频数极值的发生概率。

计算统计量步骤： （期望频数总和与观察频数总和相等）

1、表里填写相应的观察频数和期望频数

2、利用卡方公式计算检验统计量：

 

 

 

决策原则

如果位于拒绝域内我们拒绝原假设H0， 接受 H1。

如果不在拒绝域内我们 接受 原假设H0，拒绝H1

检验统计量38.272 > 9.49 位于拒绝域内

于是拒绝原假设：抽奖机每局收益如何概率分布，也就是说 抽奖机被人动了手脚

检验统计量拒绝域内外判定：

1、求出检验统计量a

2、通过自由度和显著性水平查到拒绝域临界值b

3、a>b则位于拒绝域内，反之，位于拒绝域外。

 

 

 LocalMapping.cc

            // Step 6.6：计算3D点在当前关键帧下的重投影误差
            const float &sigmaSquare1 = mpCurrentKeyFrame->mvLevelSigma2[kp1.octave];
            const float x1 = Rcw1.row(0).dot(x3Dt)+tcw1.at(0);
            const float y1 = Rcw1.row(1).dot(x3Dt)+tcw1.at(1);
            const float invz1 = 1.0/z1;

            if(!bStereo1)
            {
                // 单目情况下
                float u1 = fx1*x1*invz1+cx1;
                float v1 = fy1*y1*invz1+cy1;
                float errX1 = u1 - kp1.pt.x;
                float errY1 = v1 - kp1.pt.y;
                // 假设测量有一个像素的偏差，2自由度卡方检验阈值是5.991
                if((errX1*errX1+errY1*errY1)>5.991*sigmaSquare1)
                    continue;
            }
            else
            {
                // 双目情况
                float u1 = fx1*x1*invz1+cx1;
                // 根据视差公式计算假想的右目坐标
                float u1_r = u1 - mpCurrentKeyFrame->mbf*invz1;     
                float v1 = fy1*y1*invz1+cy1;
                float errX1 = u1 - kp1.pt.x;
                float errY1 = v1 - kp1.pt.y;
                float errX1_r = u1_r - kp1_ur;
                // 自由度为3，卡方检验阈值是7.8
                if((errX1*errX1+errY1*errY1+errX1_r*errX1_r)>7.8*sigmaSquare1)
                    continue;
            }

B站5小时orbslam

卡方检验计算置信度得分: CheckFundamental()、CheckHomography()

卡方检验通过构造检验统计量

来比较期望结果和实际结果之间的差别,从而得出观察频数极值的发生概率.

根据重投影误差构造统计量

,其值越大,观察结果和期望结果之间的差别越显著,某次计算越可能用到了外点.

统计量置信度阈值与被检验变量自由度有关: 单目特征点重投影误差的自由度为2(u,v),双目特征点重投影误差自由度为3(u,v,ur).

取95%置信度下的卡方检验统计量阈值

• 若统计量大于该阈值,则认为计算矩阵使用到了外点,将其分数设为0.
• 若统计量小于该阈值,则将统计量裕量设为该解的置信度分数.

 

float Initializer::CheckHomography(const cv::Mat &H21, const cv::Mat &H12,vector &vbMatchesInliers, float sigma) {

    const int N = mvMatches12.size();

    

    // 取出单应矩阵H各位上的值

    const float h11 = H21.at(0, 0);

    const float h12 = H21.at(0, 1);

    const float h13 = H21.at(0, 2);

    const float h21 = H21.at(1, 0);

    const float h22 = H21.at(1, 1);

    const float h23 = H21.at(1, 2);

    const float h31 = H21.at(2, 0);

    const float h32 = H21.at(2, 1);

    const float h33 = H21.at(2, 2);

​

    const float h11inv = H12.at(0, 0);

    const float h12inv = H12.at(0, 1);

    const float h13inv = H12.at(0, 2);

    const float h21inv = H12.at(1, 0);

    const float h22inv = H12.at(1, 1);

    const float h23inv = H12.at(1, 2);

    const float h31inv = H12.at(2, 0);

    const float h32inv = H12.at(2, 1);

    const float h33inv = H12.at(2, 2);

    

    vbMatchesInliers.resize(N);     // 标记是否是内点

    float score = 0;                // 置信度得分

    const float th = 5.991;         // 自由度为2,显著性水平为0.05的卡方分布对应的临界阈值

    const float invSigmaSquare = 1.0 / (sigma * sigma);     // 信息矩阵,方差平方的倒数

​

    

    // 双向投影,计算加权投影误差

    for (int i = 0; i < N; i++) {

        bool bIn = true;

​

        // step1. 提取特征点对

        const cv::KeyPoint &kp1 = mvKeys1[mvMatches12[i].first];

        const cv::KeyPoint &kp2 = mvKeys2[mvMatches12[i].second];

        const float u1 = kp1.pt.x;

        const float v1 = kp1.pt.y;

        const float u2 = kp2.pt.x;

        const float v2 = kp2.pt.y;

​

        // step2. 计算img2到img1的重投影误差

        const float w2in1inv = 1.0 / (h31inv * u2 + h32inv * v2 + h33inv);

        const float u2in1 = (h11inv * u2 + h12inv * v2 + h13inv) * w2in1inv;

        const float v2in1 = (h21inv * u2 + h22inv * v2 + h23inv) * w2in1inv;

        const float squareDist1 = (u1 - u2in1) * (u1 - u2in1) + (v1 - v2in1) * (v1 - v2in1);

        const float chiSquare1 = squareDist1 * invSigmaSquare;

​

        // step3. 离群点标记上,非离群点累加计算得分

        if (chiSquare1 > th)

            bIn = false;

        else

            score += th - chiSquare1;

​

        // step4. 计算img1到img2的重投影误差

        const float w1in2inv = 1.0 / (h31 * u1 + h32 * v1 + h33);

        const float u1in2 = (h11 * u1 + h12 * v1 + h13) * w1in2inv;

        const float v1in2 = (h21 * u1 + h22 * v1 + h23) * w1in2inv;

        const float squareDist2 = (u2 - u1in2) * (u2 - u1in2) + (v2 - v1in2) * (v2 - v1in2);

        const float chiSquare2 = squareDist2 * invSigmaSquare;

​

        // step5. 离群点标记上,非离群点累加计算得分

        if (chiSquare2 > th)

            bIn = false;

        else

            score += th - chiSquare2;

        

        

        if (bIn)

            vbMatchesInliers[i] = true;

        else

            vbMatchesInliers[i] = false;

    }

    return score;

}