共轭梯度法（Conjugate Gradients）（4）

最近在看ATOM，作者在线训练了一个分类器，用的方法是高斯牛顿法和共轭梯度法。看不懂，于是恶补了一波。学习这些东西并不难，只是难找到学习资料。简单地搜索了一下，许多文章都是一堆公式，这谁看得懂啊。

后来找到一篇《An Introduction to the Conjugate Gradient Method Without the Agonizing Pain》，解惑了。
为什么中文没有这么良心的资料呢？英文看着费劲，于是翻译过来搬到自己的博客，以便回顾。

由于原文比较长，一共 $66$ 页的PDF，所以这里分成几个部分来写。

目录
共轭梯度法（Conjugate Gradients）（1）
共轭梯度法（Conjugate Gradients）（2）
共轭梯度法（Conjugate Gradients）（3）
共轭梯度法（Conjugate Gradients）（4）
共轭梯度法（Conjugate Gradients）（5）

---

12. Preconditioning

预条件？（Preconditioning）是一种提升矩阵条件数（condition number）的技术。

假设 $M$ 是一个近似于 $A$ 的对称正定矩阵，但更容易求逆。

要求解 $Ax=b$，可以通过求解下面的式子间接得到。$$M^{(-1)}Ax=M^{(-1)}b\text{\hspace{1em}(53)}$$

如果 $\kappa (M^{(-1)}A)\ll \kappa (A)$，或者 $M^{-1}A$ 的特征值比 $A$ 的聚（clustered）得更好，我们可以比原问题更快地迭代地求解式子(53)。问题是， $M^{-1}A$ 不会通常是对称或者定（definite，正定或负定）的，尽管 $M$ 和 $A$ 都是对称或者定。

我们可以克服这个困难，因为对于每一个对称的，正定的 $M$，总是有一个（不是唯一的）矩阵 $E$ 拥有这样的特性：$E{E}^T=M$。（这样的 $E$ 是可以获得的，例如用 Cholesky 分解 ）。矩阵 $M^{-1}A$ 和矩阵 $E^{-1}A{E}^{-T}$ 有同样的特征值。这是因为，如果 $v$ 是 $M^{-1}A$ 的特征向量，特征值为 $\lambda$；则 $E^{T}v$ 就是 $E^{-1}A{E}^{-T}$ 的特征向量，特征值为 $\lambda$：
$$(E^{-1}A{E}^{-T})(E^{T}v)=(E^T{E}^{-T})E^{-1}Av=E^T{M}^{-1}Av=\lambda E^{T}v$$

$Ax=b$ 这个系统可以转换为问题：
$$E^{-1}A{E}^{-T}x=E^{-1}b,x=E^{T}x$$

首先我们求解 $x$，然后到 $x$。由于 $E^{-1}A{E}^{-T}$ 是对称和正定的，$x$ 可以用最陡下降或者共轭梯度来求。用 CG 来求解这个系统的过程称为：
Transformed Preconditioned Conjugate Gradient Method
（变换预条件共轭梯度法）：
$${\hat{d}}_{(0)}={\hat{r}}_{(0)}=E^{-1}b-E^{-1}A{E}^{-T}{\hat{x}}_{(0)}$$ $${\alpha }_{(i)}=\frac{{\hat{r}}_{(i)}^T{\hat{r}}_{(i)}}{{\hat{d}}_{(i)}^T{E}^{-1}A{E}^{-T}{\hat{d}}_{(i)}}$$ $${\hat{x}}_{(i+1)}={\hat{x}}_{(i)}+{\alpha }_{(i)}{\hat{d}}_{(i)}$$ $${\hat{r}}_{(i+1)}={\hat{r}}_{(i)}-{\alpha }_{(i)}{E}^{-1}A{E}^{-T}{\hat{d}}_{(i)}$$ $${\beta }_{(i+1)}=\frac{{\hat{r}}_{(i+1)}^T{\hat{r}}_{(i+1)}}{{\hat{r}}_{(i)}^T{\hat{r}}_{(i)}}$$ $${\hat{d}}_{(i+1)}={\hat{r}}_{(i+1)}+{\beta }_{(i+1)}{\hat{d}}_{(i)}$$

这种方法有一个你不希望的特点，就是必须算出 $E$。然而，有一些细心的变量替换可以消掉 $E$。令 ${\hat{r}}_{(i)}=E^{-1}{r}_{(i)}$ 以及 ${\hat{d}}_{(i)}=E^T{d}_{(i)}$，然后利用等式 ${\hat{x}}_{(i)}=E^T{x}_{(i)}$ 和 $E^{-T}{E}^{-1}=M^{-1}$，我们推导出 Untransformed Preconditioned Conjugate Gradient Method（未变换的预条件共轭梯度法）：
$$r_{(0)}=b-A{x}_{(0)}$$ $$d_{(0)}=M^{-1}{r}_{(0)}$$ $${\alpha }_{(i)}=\frac{r_{(i)}^T{M}^{-1}{r}_{(i)}}{d_{(i)}^{T}A{d}_{(i)}}$$ $$x_{(i+1)}=x_{(i)}+{\alpha }_{(i)}{d}_{(i)}$$ $$r_{(i+1)}=r_{(i)}-{\alpha }_{(i)}A{d}_{(i)}$$ $${\beta }_{(i+1)}=\frac{r_{(i+1)}^T{M}^{-1}{r}_{(i+1)}}{r_{(i)}^T{M}^{-1}{r}_{(i)}}$$ $$d_{(i+1)}=M^{-1}{r}_{(i+1)}+{\beta }_{(i+1)}{d}_{(i)}$$

矩阵 $E$ 没有出现在这些式子里了；只有 $M^{-1}$ 是需要算的。同理，你也可以导出不需要 $E$ 的 Preconditioned Steepest Descent Method。

预条件者（preconditioner）$M$ 的有效性由条件数 （condition number）$M^{-1}A$ 决定，偶尔也取决于特征值聚的情况（clustering）。

剩下的问题是找到一个 preconditioner 能够足够地近似 $A$，以充分地提高收敛性，在每一次迭代中弥补计算 $M^{-1}{r}_{(i)}$ 的成本。（不需要显式地计算 $M$ 或者 $M^{-1}$，只需要计算 $M^{-1}$ 乘上一个向量的效果）。在这样的约束下，在这种约束下，有惊人的丰富的可能性提供，而我在此仅能触到及一些皮毛。

直观地说，预处理（preconditioning）是一种试图拉伸二次型，使其看起来更球形，从而使特征值相互靠近。 最好的预条件者（preconditioner）是 $M=A$；对于这个预条件者，$M^{-1}A$ 有一个条件数（condition number），那就是 $1$，然后二次型是完全的球形，所以求解只需要一次迭代。可惜的是，预条件这一步解决的是系统 $Mx=b$，所以这根本不是一个有用的预条件者（preconditioner）。

最简单的预条件者（preconditioner）是一个对角矩阵，其中对角项与 $A$ 的对角项完全相同。采用这种预条件者（preconditioner）的过程被称为对角预条件（diagonal preconditioning）或者叫雅克比预条件（Jacobi preconditioning），等价于沿着坐标轴缩放二次型。（相比之下，完美预条件者（perfect preconditioner）$M=A$ 是沿着特征向量的轴来缩放二次型。）$A$ 对角矩阵很容易求逆，但通常只是一个普通的预条件者（preconditioner）。经过对角预条件（diagonal preconditioning）之后，我们的例子的等高线如 图(36) 所示。

(图36)

与 图(3) 相比，很明显，已经发生了一些改善。条件数（condition number）从 $3.5$ 提升到了大概 $2.8$。当然，对于 $n\gg 2$ 的系统会得到更多的提升。

还有一种更复杂的预条件者（preconditioner），是不完整的 Cholesky 预条件（incomplete Cholesky preconditioning）。

Cholesky 因式分解（Cholesky factorization）是一种把矩阵 $A$ 分解成形式 $L{L}^T$ 的技术，其中 $L$ 是一个下三角矩阵。不完整 Cholesky 因式分解是一种变体，允许很少或者不填充。 $A$ 由 $\hat{L}{\hat{L}}^T$ 来近似，其中 $\hat{L}$ 可能被限制为具有与 $A$ 相同的非零元素模式；$L$ 的其它元素配抛弃掉了。为了把 $\hat{L}{\hat{L}}^T$ 作为预条件者（preconditioner）， $\hat{L}{\hat{L}}^T\omega =z$ 的解是通过回代来求得的。（$\hat{L}{\hat{L}}^T$ 的逆不需要被显式地计算）。然而，incomplete Cholesky preconditioning 并不总是稳定。

现在开发出来了许多 preconditioner ，有一些十分复杂，无论你用不用，对于大规模的应用，人们普遍认为 CG 应该与 preconditioner 一起使用。

13. Conjugate Gradients on the Normal Equations
（正规方程上的共轭梯度）

CG 可以用于求解这样的线性系统：其中 $A$ 不对称，不正定，甚至不是方阵。

对于最小二乘问题：$$\underset{x}{\min }\Vert Ax-b{\Vert }^2\text{\hspace{1em}(54)}$$

可以通过把 式子(54) 的导数设为 $0$ 来求解：$$A^{T}Ax=A^{T}b\text{\hspace{1em}(55)}$$

如果 $A$ 是方形、非奇异的，那 式子(55) 的解就是 $Ax=b$ 的解。

如果 $A$ 不是方形，且 $Ax=b$ 是 overconstrained 的（即线性无关方程的数量比变量的数量多，或者叫超定？Overdetermined system？），那 式子(55) 的解就不一定是 $Ax=b$ 的解。不过，我们总是可以找到一个 $x$ 使 式子(54) —— 每个线性方程的平方误差和（sum of the squares of the errors ） 最小化。

$A^{T}A$ 是对称且正定的（对于任意 $x$，$x^T{A}^{T}Ax=\Vert Ax{\Vert }^2\ge 0$）。如果 $Ax=b$ 不是 underconstrained 的，那 $A^{T}A$ 是非奇异的，那像最陡下降和共轭梯度这样的方法可以用于求解 式子(55)。这么做的唯一麻烦就是 $A^{T}A$ 的条件数（condition number ）是 $A$ 的条件数的平方，因此收敛速度明显较慢。

一个重要的技术点是，矩阵 $A^{T}A$ 没有被显式地形成，因为它没有 $A$ 那么稀疏。相反，对于式子 $A^{T}Ad$ ，我们首先是求 $Ad$，然后再求 $A^{T}Ad$。如果我们通过 $Ad$ 和自己的内积来求 $d^T{A}^{T}Ad$（它在式子(46)l里），那么数值稳定性就会提升。

14. The Nonlinear Conjugate Gradient Method
（非线性共轭梯度法）

CG 不仅能被用于求解二次型问题的最小值，还可以用于最小化任何函数 $f(x)$，只要能计算它的梯度 $f^{\prime }$ 。

它能用于各种各样的优化问题，例如工程设计，训练神经网络，非线性回归等。

14.1 Outline of the Nonlinear Conjugate Gradient Method
（非线性共轭梯度法的概述）

为了推导非线性的 CG，对线性算法做 $3$ 个改动：用于计算残差的递归公式不能用了。计算步长 $\alpha$ 的方法更加复杂。对于 $\beta$ 的选择也有一些不同。

在非线性 CG 中，残差总是设为负的梯度：$r_{(i)}=-f^{\prime }(x_{(i)})$

搜索方向的计算和线性 CG 里面一样，用残差的格拉姆-施密特共轭（Gram-Schmidt conjugation）来计算。沿着这个搜索方向执行线搜索（line search）比线性情况要困难得多，并且有多种过程可以使用。

和线性 CG 里面一样，通过确保梯度和搜索方向正交，来找到 ${\alpha }_{(i)}$ 使 $f(x_{(i)}+{\alpha }_{(i)}{d}_{(i)})$ 最小化。我们可以使用任何算法来找到式子 $[f^{\prime }(x_{(i)}+{\alpha }_{(i)}{d}_{(i)}){]}^T{d}_{(i)}$ 的零点。

在线性 CG 里，$\beta$ 有几个等价的表达式。 在非线性 CG 里，这些表达式不再等价；研究者们仍然在寻求最好的选择。有两种可选的做法，一个是 Fletcher-Reeves 公式，另一个是 Polak-Ribière 公式：$${\beta }_{(i+1)}^{FR}=\frac{r_{(i+1)}^T{r}_{(i+1)}}{r_{(i)}^T{r}_{(i)}},{\beta }_{(i+1)}^{PR}=\frac{r_{(i+1)}^T(r_{(i+1}-r_{(i)})}{r_{(i)}^T{r}_{(i)}}$$

如果初始点足够接近所期望的最小值，那么 Fletcher-Reeves 法可以收敛。但在那里 Polak-Ribière 法在少数情况下会无限循环，得不到收敛。不过 Polak-Ribière 法常常会收敛得更快。

幸运的是，令 $\beta =\max \{{\beta }^{PR},0\}$ 可以保证 Polak-Ribière 法收敛。如果 ${\beta }^{PR}<0$，使用该值相当于重启 CG。重启 CG 就是忘掉过去的搜索方向，并向最陡下降的方向重新开始 CG。

下面是非线性共轭梯度法的概览：$$d_{(0)}=r_{(0)}=-f^{\prime }(x_{(0)}),$$ $$\text{Find}{\alpha }_{(i)}\text{that minimizes}f(x_{(i)}+{\alpha }_{(i)}{d}_{(i)}),$$ $$x_{(i+1)}=x_{(i)}+{\alpha }_{(i)}{d}_{(i)},$$ $$r_{(i+1)}=-f^{\prime }(x_{(i+1)}),$$ $${\beta }_{(i+1)}=\frac{r_{(i+1)}^T{r}_{(i+1)}}{r_{(i)}^T{r}_{(i)}}\text{or}{\beta }_{(i+1)}=\max \left\{\frac{r_{(i+1)}^T(r_{(i+1)}-r_{(i)})}{r_{(i)}^T{r}_{(i)}},0\right\}$$ $$d_{(i+1)}=r_{(i+1)}+{\beta }_{(i+1)}{d}_{(i)}$$

非线性 CG 不像线性 CG 那么能保证收敛。$f$ 与二次函数越不像，搜索方向就会越快失去共轭性。（很快就会清楚，“共轭（conjugacy）”在非线性 CG 中仍然有一些意义。）

另外一个问题是，一般性的函数 $f$ 可能有许多局部最小值。CG 不能保证收敛到全局最小值。如果 $f$ 没有下界，甚至可能找不到局部最小值。

(图37)

图(37) 展示了非线性 CG。
图(37)a 的方程有多个局部最小值。
图(37)b 展示了用 Fletcher-Reeves 公式时，非线性 CG 的收敛情况。在这个例子里， CG 几乎不像线性的情况那么有效；这个函数似乎很难最小化。
图(37)c 展示了一个横截面，对应于 图(37)b 的第一条线搜索。注意到会有好几个极小值，线搜索会找到一个 $\alpha$ ，对应于附近的最小值。
图(37)d 展示了 Polak-Ribière CG 的优越的收敛情况。

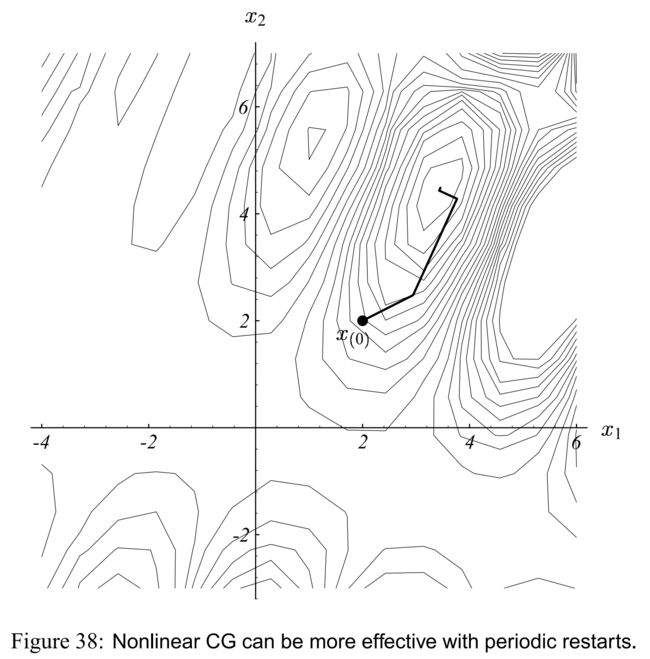
由于 CG 只能在 $n$ 维空间生成 $n$ 个共轭向量， 所以每 $n$ 次迭代后重启 CG 是有意义的，特别是 $n$ 很小的时候。图(38) 展示了非线性 CG 每第二次迭代就重启的效果。（对于这个特殊的例子， Fletcher-Reeves 法和 Polak-Ribière 法的表现都是一样的）

(图38)

14.2 General Line Search（一般的线搜索）

依赖 $f^{\prime }$ 的值，我们有机会使用一个快速的算法来找到 $f^{\prime T}d$ 的零点。

例如，如果 $f^{\prime }$ 是 $\alpha$ 中的多项式，那就能用上高效的算法进行多项式的寻零（zero-finding）。

然而，我们将会仅考虑通用性的算法。

两种寻零（zero-finding）的迭代法分别是牛顿-拉夫森（Newton-Raphson）算法和弦截（Secant）法。两种算法都要求 $f$ 二阶连续可微。 牛顿-拉夫森（Newton-Raphson） 算法还会要求求 $f(x+\alpha d)$ 关于 $\alpha$ 的二阶导。

牛顿-拉夫森（Newton-Raphson） 算法依赖于泰勒级数（Taylor series）的近似

$$\begin{array}{rl}f(x+\alpha d)& \approx f(x)+\alpha {\left[\frac{d}{d\alpha }f(x+\alpha d)\right]}_{\alpha =0}+\frac{{\alpha }^2}{2}{\left[\frac{d^2}{d{\alpha }^2}f(x+\alpha d)\right]}_{\alpha =0}(56)\\ & =f(x)+\alpha [f^{\prime }(x){]}^{T}d+\frac{{\alpha }^2}{2}{d}^T{f}^{\prime \prime }(x)d\\ \frac{d}{d\alpha }f(x+\alpha d)& \approx [f^{\prime }(x){]}^{T}d+\alpha d^T{f}^{\prime \prime }(x)d.(57)\end{array}$$

其中 $f^{\prime \prime }(x)$ 为海森矩阵（Hessian matrix）：
$$f^{\prime \prime }(x)=\left[\begin{array}{cccc}\frac{{\partial }^{2}f}{\partial x_1\partial x_1}& \frac{{\partial }^{2}f}{\partial x_1\partial x_2}& \cdots & \frac{{\partial }^{2}f}{\partial x_1\partial x_n}\\ \frac{{\partial }^{2}f}{\partial x_2\partial x_1}& \frac{{\partial }^{2}f}{\partial x_2\partial x_2}& \cdots & \frac{{\partial }^{2}f}{\partial x_2\partial x_n}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{{\partial }^{2}f}{\partial x_n\partial x_1}& \frac{{\partial }^{2}f}{\partial x_n\partial x_2}& \cdots & \frac{{\partial }^{2}f}{\partial x_n\partial x_n}\end{array}\right]$$

通过将 式子(57) 置零，可以将函数 $f(x+\alpha d)$ 近似最小化，给定：$$\alpha =-\frac{f^{\prime T}d}{d^T{f}^{{}^{\prime \prime }}d}$$

截断的泰勒级数通过一个抛物面近似 $f(x+\alpha d)$，我们走到抛物面的底部,，见 图(39)。实际上，如果 $f$ 是一个二次型，那么这个抛物线近似是精确的，因为 $f^{\prime \prime }$ 就是我们熟悉的矩阵 $A$。通常来讲，如果搜索方向都是 $f{}^{\prime \prime }$-正交的，那么这些搜索方向就共轭（conjugate）。

(图39)

“共轭（conjugate）” 的含义一直在变化，因为 $f{}^{\prime \prime }$ 是随着 $x$ 而变化的。 $f{}^{\prime \prime }$ 随 $x$ 变化得越快，搜索方向就越快失去共轭性（conjugacy）。另一方面，$x_{(i)}$ 越接近解，每次迭代的 $f{}^{\prime \prime }$ 就变化越小。起始点越靠近解，非线性 CG 和线性 CG 的收敛性就越像。

为了在非二次型的方程上进行精确的线搜索，必须沿着搜索线重复地走，知道 $f^{\prime T}d$ 为 $0$。因此，一个 CG 的迭代可能包含许多次 牛顿-拉夫森（Newton-Raphson）迭代。 必须在每一步都计算$f^{\prime }Td$ 和 $d^{T}f{}^{\prime \prime }d$ 的值。如果 $d^{T}f{}^{\prime \prime }d$ 可以被解析性地简化，那么这些计算就没什么开销。但如果必须计算完整的矩阵 $f{}^{\prime \prime }$，那算法就会很慢。对于某些应用，可以通过仅用 $f{}^{\prime \prime }$ 的对角元素来进行近似的线搜索，来规避这个问题。当然，有一些函数根本不可能计算 $f{}^{\prime \prime }$。

为了进行精确的线搜索而不计算 $f{}^{\prime \prime }$，弦截（Secant）法通过在不同的两点 $\alpha =0$ 和 $\alpha =\sigma$ 计算 $f(x+\alpha d)$ 的一阶导，来近似 $f(x+\alpha d)$ 的二阶导。其中 $\sigma$ 是任意小的非零数：$$\begin{array}{rl}\frac{d^2}{d{\alpha }^2}f(x+\alpha d)& \approx \frac{{\left[\frac{d}{d\alpha }f(x+\alpha d)\right]}_{\alpha =\sigma }-{\left[\frac{d}{d\alpha }f(x+\alpha d)\right]}_{\alpha =0}}{\sigma }\sigma \ne 0\\ & =\frac{{\left[f^{\prime }(x+\sigma d)\right]}^{T}d-[f^{\prime }(x){]}^{T}d}{\sigma }\end{array}\text{\hspace{1em}(58)}$$

其中当 $\alpha$ 和 $\sigma$ 逼近 $0$ 的时候，它能更好地近似二阶导。

如果我们用 式子(58) 来替代泰勒展开式（式子(56)）中的第 $3$ 项，就有：$$\frac{d}{d\alpha }f(x+\alpha d)\approx [f^{\prime }(x){]}^{T}d+\frac{\alpha }{\sigma }\left\{[f^{\prime }(x+\sigma d){]}^{T}d-[f^{\prime }(x){]}^{T}d\right\}$$

通过将 $f(x+\alpha d)$ 的导数置 $0$ 来最小化它：$$\alpha =-\sigma \frac{[f^{\prime }(x{)}^T]d}{[f^{\prime }(x+\sigma d){]}^{T}d-[f^{\prime }(x){]}^{T}d}\text{\hspace{1em}(59)}$$

像 牛顿-拉夫森（Newton-Raphson） 法一样，弦截（Secant）法也用一个抛物线（parabola）来近似 $f(x+\alpha d)$。但是 弦截法 不是通过在 $1$ 个点上求一阶和二阶导来找到抛物线，而是在两个不同的点上求一阶导，见 图(40)。

(图40)

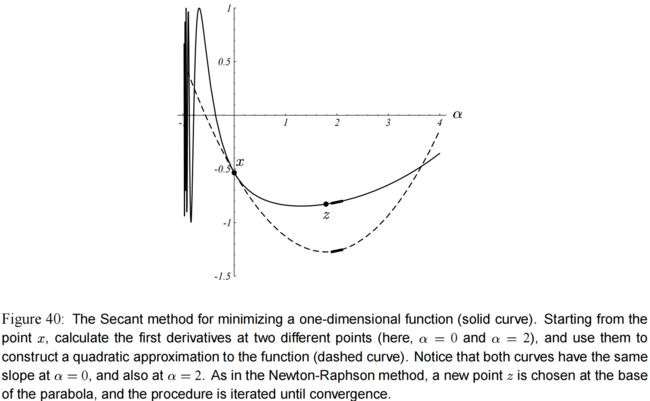
通常，我们在弦截（Secant）法的第一个迭代中选择任意的 $\sigma$；在后续迭代中，我们选择 $x+\sigma d$ 作为上一次弦截（Secant）迭代法的 $x$ 的值。换句话说，如果我们令 ${\alpha }_{[i]}$ 表示在弦截法第 $i$ 次迭代中算出来的 $\alpha$ 的值，那么 ${\sigma }_{[i+1]}=-{\alpha }_{[i]}$。

当 $x$ 足够接近精确解时，牛顿-拉夫森（Newton-Raphson） 法和 弦截（Secant）法都应当终止。

当要求的精度过低，可能会导致收敛失败，但是要求的精度太高会导致计算很慢，而且没有任何收获。因为如果 $f^{\prime \prime }(x)$ 随 x 变化很大，共轭性将很快崩溃。因此，进行快而不精确的线搜索往往是更好的策略（例如，固定 Newton-Raphson 和 Secant 法的迭代次数 ）。不幸的是，不精确的线搜索可能会导致，构建的搜索方向不是下降的方向。一个常见的解决方案是测试这种可能性：$r^{T}d$ 是负的吗？然后有必要的话，通过令 $d=r$ 重启 CG。

两种方法都有一个更大的问题，就是他们不能区分最小值和最大值。非线性 CG 的结果通常严重依赖初始位置，如果用 Newton-Raphson 或者 Secant 法的 CG 从局部最大值的附近开始，它可能会收敛到那个点上。

两种方法各有优点，Newton-Raphson 法收敛速度更快，如果能够很快地计算 $d^T{f}^{\prime \prime }d$ （或者能很好地近似），例如时间复杂度在 $\mathcal{O}(n)$ 以内，那么首选Newton-Raphson法。

Secant 法只需要求 $f$ 的一阶导，但是它能否成功，取决于参数 $\sigma$ 选得好不好。

其它的方法也很容易推导出来，例如，通过在 $3$ 个不同的点采样 $f$，有可能产生一个抛物线来近似 $f(x+\alpha d)$，甚至不需要求 $f$ 的一阶导。

14.3 Preconditioning

可以通过选择一个预条件者（preconditioner）$M$ 来预条件（preconditioning）非线性 CG，对这个 $M$ 的要求是，$M$ 要近似于 $f^{\prime \prime }$，且要使 $M^{-1}r$ 容易计算。

在线性 CG 中，预条件者（preconditioner）试图将二次型变换，使其变得像一个球型。
在非线性 CG 中，预条件者（preconditioner）是在 $x_{(i)}$ 的一个邻域上做这个变换的。

计算完整的海森矩阵（Hessian Matrix）$f^{\prime \prime }$ 开销很大，通常计算它的对角线来作为预条件者（preconditioner）。然而，要提前告诉你的是，如果 $x$ 距离局部最小值足够远，海森矩阵的对角元素可能不是全为正数。预条件者（preconditioner）应该是正定的，所以不允许有负的对角元素。一个保守的解决方案是，当无法保证海森矩阵是正定的时候，那就不做预条件（precondition）（令 $M=I$）。

(图40)

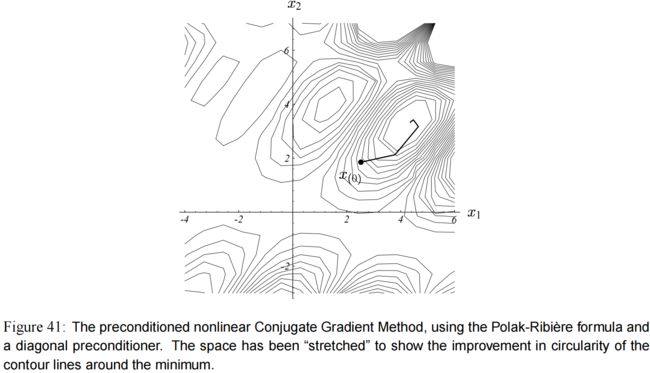
图(41) 展示的是对角预条件的非线性共轭梯度（diagonally preconditioned nonlinear CG） 的收敛情况，用的是 Polak-Ribière 法，和 图(37) 中的方程一样。这里我作弊了一下，在每次迭代中，在解点 $x$ 处用 $f^{\prime \prime }$ 的对角元素来预条件（precondition）。