读书笔记:Algorithms for Decision Making(14)
读书笔记:Algorithms for Decision Making
上一篇 读书笔记:Algorithms for Decision Making(13)
目录
- 读书笔记:Algorithms for Decision Making
- 五、多智能体系统(3)
-
- 3. 状态不确定
-
- 3.1 Partially Observable Markov Games
- 3.2 策略进化
-
- 3.2.1 基于树的条件规划的策略
- 3.2.2 基于图的控制器的策略
- 3.3 Nash 均衡
- 3.4 动态规划
- 4. Decentralized Partially Observable Markov Decision Processes
-
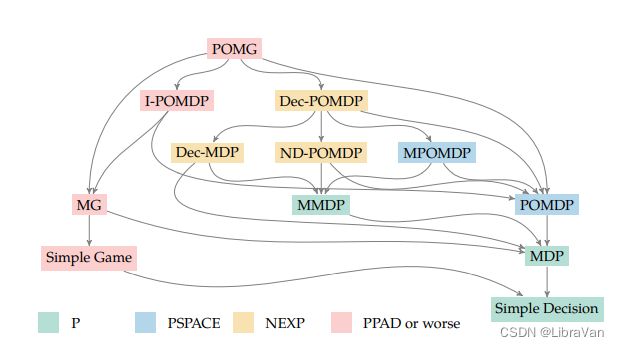
- 4.1 Subclass
- 4.2 算法
-
- 4.2.1 动态规划
- 4.2.2 迭代最佳响应
- 4.2.3 Heuristic Search
- 4.2.4 非线性规划
- 总结
五、多智能体系统(3)
本部分将简单游戏扩展到具有多个状态的连续上下文。马尔可夫博弈可以看作是多个具有自己奖励函数的智能体的马尔可夫决策过程。
3. 状态不确定
3.1 Partially Observable Markov Games
POMG可以看作是MG到部分可观测性的扩展,也可以看作是POMDP到多个代理的扩展。
struct POMG
γ # discount factor
ℐ # agents
# state space
# joint action space
# joint observation space
T # transition function
O # joint observation function
R # joint reward function
end
3.2 策略进化
3.2.1 基于树的条件规划的策略
function lookahead(::POMG, U, s, a)
, , T, O, R, γ = ., joint(.), .T, .O, .R, .γ
u′ = sum(T(s,a,s′)*sum(O(a,s′,o)*U(o,s′) for o in ) for s′ in )
return R(s,a) + γ*u′
end
function evaluate_plan(::POMG, π, s)
a = Tuple(πi() for πi in π)
U(o,s′) = evaluate_plan(, [πi(oi) for (πi, oi) in zip(π,o)], s′)
return isempty(first(π).subplans) ? .R(s,a) : lookahead(, U, s, a)
end
function utility(::POMG, b, π)
u = [evaluate_plan(, π, s) for s in .]
return sum(bs * us for (bs, us) in zip(b, u))
end
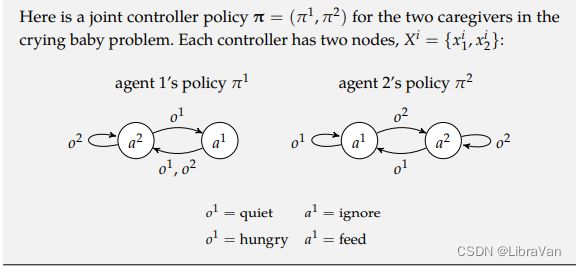
3.2.2 基于图的控制器的策略
3.3 Nash 均衡
struct POMGNashEquilibrium
b # initial belief
d # depth of conditional plans
end
function create_conditional_plans(, d)
ℐ, , = .ℐ, ., .
Π = [[ConditionalPlan(ai) for ai in [i]] for i in ℐ]
for t in 1:d
Π = expand_conditional_plans(, Π)
end
return Π
end
function expand_conditional_plans(, Π)
ℐ, , = .ℐ, ., .
return [[ConditionalPlan(ai, Dict(oi => πi for oi in [i]))
for πi in Π[i] for ai in [i]] for i in ℐ]
end
function solve(M::POMGNashEquilibrium, ::POMG)
ℐ, γ, b, d = .ℐ, .γ, M.b, M.d
Π = create_conditional_plans(, d)
U = Dict(π => utility(, b, π) for π in joint(Π))
= SimpleGame(γ, ℐ, Π, π -> U[π])
π = solve(NashEquilibrium(), )
return Tuple(argmax(πi.p) for πi in π)
end
3.4 动态规划
struct POMGDynamicProgramming
b # initial belief
d # depth of conditional plans
end
function solve(M::POMGDynamicProgramming, ::POMG)
ℐ, , , R, γ, b, d = .ℐ, ., ., .R, .γ, M.b, M.d
Π = [[ConditionalPlan(ai) for ai in [i]] for i in ℐ]
for t in 1:d
Π = expand_conditional_plans(, Π)
prune_dominated!(Π, )
end
= SimpleGame(γ, ℐ, Π, π -> utility(, b, π))
π = solve(NashEquilibrium(), )
return Tuple(argmax(πi.p) for πi in π)
end
function prune_dominated!(Π, ::POMG)
done = false
while !done
done = true
for i in shuffle(.ℐ)
for πi in shuffle(Π[i])
if length(Π[i]) > 1 && is_dominated(, Π, i, πi)
filter!(πi′ -> πi′ ≠ πi, Π[i])
done = false
break
end
end
end
end
end
function is_dominated(::POMG, Π, i, πi)
ℐ, = .ℐ, .
jointΠnoti = joint([Π[j] for j in ℐ if j ≠ i])
π(πi′, πnoti) = [j==i ? πi′ : πnoti[j>i ? j-1 : j] for j in ℐ]
Ui = Dict((πi′, πnoti, s) => evaluate_plan(, π(πi′, πnoti), s)[i]
for πi′ in Π[i], πnoti in jointΠnoti, s in )
model = Model(Ipopt.Optimizer)
@variable(model, δ)
@variable(model, b[jointΠnoti, ] ≥ 0)
@objective(model, Max, δ)
@constraint(model, [πi′=Π[i]],
sum(b[πnoti, s] * (Ui[πi′, πnoti, s] - Ui[πi, πnoti, s])
for πnoti in jointΠnoti for s in ) ≥ δ)
@constraint(model, sum(b) == 1)
optimize!(model)
return value(δ) ≥ 0
end
4. Decentralized Partially Observable Markov Decision Processes
Dec-POMDP是所有智能体都共享相同目标的POMG。
struct DecPOMDP
γ # discount factor
ℐ # agents
# state space
# joint action space
# joint observation space
T # transition function
O # joint observation function
R # reward function
end
4.1 Subclass
4.2 算法
4.2.1 动态规划
struct DecPOMDPDynamicProgramming
b # initial belief
d # depth of conditional plans
end
function solve(M::DecPOMDPDynamicProgramming, ::DecPOMDP)
ℐ, , , , T, O, R, γ = .ℐ, ., ., ., .T, .O, .R, .γ
R′(s, a) = [R(s, a) for i in ℐ]
′ = POMG(γ, ℐ, , , , T, O, R′)
M′ = POMGDynamicProgramming(M.b, M.d)
return solve(M′, ′)
end
4.2.2 迭代最佳响应
struct DecPOMDPIteratedBestResponse
b # initial belief
d # depth of conditional plans
k_max # number of iterations
end
function solve(M::DecPOMDPIteratedBestResponse, ::DecPOMDP)
ℐ, , , , T, O, R, γ = .ℐ, ., ., ., .T, .O, .R, .γ
b, d, k_max = M.b, M.d, M.k_max
R′(s, a) = [R(s, a) for i in ℐ]
′ = POMG(γ, ℐ, , , , T, O, R′)
Π = create_conditional_plans(, d)
π = [rand(Π[i]) for i in ℐ]
for k in 1:k_max
for i in shuffle(ℐ)
π′(πi) = Tuple(j == i ? πi : π[j] for j in ℐ)
Ui(πi) = utility(′, b, π′(πi))[i]
π[i] = argmax(Ui, Π[i])
end
end
return Tuple(π)
end
4.2.3 Heuristic Search
struct DecPOMDPHeuristicSearch
b # initial belief
d # depth of conditional plans
π_max # number of policies
end
function solve(M::DecPOMDPHeuristicSearch, ::DecPOMDP)
ℐ, , , , T, O, R, γ = .ℐ, ., ., ., .T, .O, .R, .γ
b, d, π_max = M.b, M.d, M.π_max
R′(s, a) = [R(s, a) for i in ℐ]
′ = POMG(γ, ℐ, , , , T, O, R′)
Π = [[ConditionalPlan(ai) for ai in [i]] for i in ℐ]
for t in 1:d
allΠ = expand_conditional_plans(, Π)
Π = [[] for i in ℐ]
for z in 1:π_max
b′ = explore(M, , t)
π = argmax(π -> first(utility(′, b′, π)), joint(allΠ))
for i in ℐ
push!(Π[i], π[i])
filter!(πi -> πi != π[i], allΠ[i])
end
end
end
return argmax(π -> first(utility(′, b, π)), joint(Π))
end
function explore(M::DecPOMDPHeuristicSearch, ::DecPOMDP, t)
ℐ, , , , T, O, R, γ = .ℐ, ., ., ., .T, .O, .R, .γ
b = copy(M.b)
b′ = similar(b)
s = rand(SetCategorical(, b))
for τ in 1:t
a = Tuple(rand(i) for i in )
s′ = rand(SetCategorical(, [T(s,a,s′) for s′ in ]))
o = rand(SetCategorical(joint(), [O(a,s′,o) for o in joint()]))
for (i′, s′) in enumerate()
po = O(a, s′, o)
b′[i′] = po*sum(T(s,a,s′)*b[i] for (i,s) in enumerate())
end
normalize!(b′, 1)
b, s = b′, s′
end
return b′
end
4.2.4 非线性规划
struct DecPOMDPNonlinearProgramming
b # initial belief
ℓ # number of nodes for each agent
end
function tensorform(::DecPOMDP)
ℐ, , , , R, T, O = .ℐ, ., ., ., .R, .T, .O
ℐ′ = eachindex(ℐ)
′ = eachindex()
′ = [eachindex(i) for i in ]
′ = [eachindex(i) for i in ]
R′ = [R(s,a) for s in , a in joint()]
T′ = [T(s,a,s′) for s in , a in joint(), s′ in ]
O′ = [O(a,s′,o) for a in joint(), s′ in , o in joint()]
return ℐ′, ′, ′, ′, R′, T′, O′
end
function solve(M::DecPOMDPNonlinearProgramming, ::DecPOMDP)
, γ, b = , .γ, M.b
ℐ, , , , R, T, O = tensorform()
X = [collect(1:M.ℓ) for i in ℐ]
jointX, joint, joint = joint(X), joint(), joint()
x1 = jointX[1]
model = Model(Ipopt.Optimizer)
@variable(model, U[jointX,])
@variable(model, ψ[i=ℐ,X[i],[i]] ≥ 0)
@variable(model, η[i=ℐ,X[i],[i],[i],X[i]] ≥ 0)
@objective(model, Max, b⋅U[x1,:])
@NLconstraint(model, [x=jointX,s=],
U[x,s] == (sum(prod(ψ[i,x[i],a[i]] for i in ℐ)
*(R[s,y] + γ*sum(T[s,y,s′]*sum(O[y,s′,z]
*sum(prod(η[i,x[i],a[i],o[i],x′[i]] for i in ℐ)
*U[x′,s′] for x′ in jointX)
for (z, o) in enumerate(joint)) for s′ in ))
for (y, a) in enumerate(joint))))
@constraint(model, [i=ℐ,xi=X[i]], sum(ψ[i,xi,ai] for ai in [i]) == 1)
@constraint(model, [i=ℐ,xi=X[i],ai=[i],oi=[i]],
sum(η[i,xi,ai,oi,xi′] for xi′ in X[i]) == 1)
optimize!(model)
ψ′, η′ = value.(ψ), value.(η)
return [ControllerPolicy(, X[i],
Dict((xi,.[i][ai]) => ψ′[i,xi,ai] for xi in X[i], ai in [i]),
Dict((xi,.[i][ai],.[i][oi],xi′) => η′[i,xi,ai,oi,xi′]
for xi in X[i], ai in [i], oi in [i], xi′ in X[i])) for i in ℐ]
end
总结
最后一部分可以看作是一个全文总结的案例,也可以看作是全文内容的升华(从单智能体到多智能体)。