图神经网络-GCN

GCN

1、图基础（Basic Knowledge of Graph）

1.1 图（Graphs）

​ 图（无论是有向图还是无向图）均是由顶点V和边E构成的集合，边可以是带权重的也可以是不带权重的，下面给出一个例子。

​ 在上图中，我们有顶点集$$V=\{A,B,C,D,E,F,G\}$$和边集$$E=\{(A,B),(B,C),(C,E),(B,D),(E,F),(D,E),(B,E),(G,E)\}$$，边上的数字代表了具体的权重，这些权重代表着不同的数量，例如，我们把结点看成各城市，边就可以看成这些城市之间不同的距离。

1.2 术语（Terminology）

• 顶点（Node）:顶点是图中的实体。
• 边（Edge）:边是连接两个顶点的线段，边可以反映两个顶点之间的关系。
• 顶点的度（Degree of a vertex）:$$G$$中顶点$$V$$的度$$d(v)$$指$$G$$中与v关联的边的数目。例如在本节第一个有向图中B点的入度为1，出度为3，在本节第二个无向图中，B点的度为3。
• 邻接矩阵（Adjacency Matrix）:邻接矩阵是表示顶点之间相邻关系的矩阵。对于含有N个结点的图，其邻接矩阵有N行N列。如果两个顶点之间存在一条边，那么就把1放在这个位置上，如果边不存在，那么就赋值为0。

2、图卷积神经网络（GCN）

2.1 2维卷积核图卷积对比

​ 现实世界中，大多数的关系本质上可以用图来表示，比如社交网络、蛋白质分子结构、万维网等。因此，使用图学习解决这些特定领域的任务可以为我们提供有效地信息。

​ 但是为什么图学习不能被像卷积神经网络那样传统的机器学习和深度学习算法来解决呢？为什么需要建立一个全新的网络类别呢？

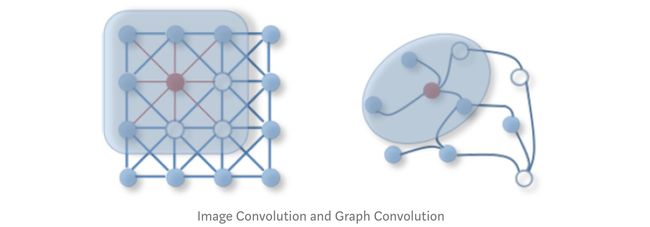
​ ①在图像为代表的欧式空间中，结点的邻居数量都是固定的。比如说绿色结点的邻居始终是8个（边缘上的点可以做Padding填充）。但是在非欧几里得空间中，结点有多少邻居并不固定，上图中目前绿色结点的邻居结点有2个，但其他结点存在5个邻居的情况。②欧式空间中的卷积操作实际上是用固定大小可学习的卷积核来抽取像素的特征，比如这里就是抽取绿色结点对应像素及其相邻像素点的特征，但是因为图里的邻居结点不固定，所以传统的卷积核不能直接用于抽取图上结点的特征。

回答上述问题之前，我们需要知道卷积神经网络的工作原理（CNNs work）.卷积神经网络是十分有用的，并且他们有足够的能力去学习到高维数据特征。如果你有一个512px*512px的图像，那么维度几乎已经一百万了。对于10个样本，特征空间就会变成$10^{1,000,000}$（Why?），目前CNNS已经证明了有足够大的能力来解决这类问题。

​ 但是有一个问题，卷积神经网络中往往有特定的结构来提取像图像、视频、音频这类数据的特征并将它们提供给分类器。

​ 什么是组合性？

​ 组合性至少含有以下属性：1.位置 2.稳定及转换不变性 3.多尺度：学习表示的层次结构

2.2图卷积神经网络的应用（Applications of GCNs）

​ GCN被用于Facebook的好友预测算法中，我们假设有三个人$$A、B、C$$，已知$$A$$是$$B$$的朋友，$$B$$是$$C$$的朋友，你还知道每个人的其它特征，比如A喜欢电影明星Liam Neeson，C是genre Thriller的粉丝，我们就能预测A是否是C的朋友。

2.3 什么是图卷积神经网络？（What GCNs?）

​ 图卷积神经网络，顾名思义，在非欧几里得空间中借鉴了卷积神经网络的思想。常规的卷积神经网络通过捕捉图像各个像素周围的信息来识别图像。与图像这样的欧几里得空间相似，图卷积的目标是在非欧几里得空间中捕捉图结点周围邻居的信息。

​ GCN是一种操作图的神经网络，它通过将图像作为输入并给出一些有用的输出。

GCN有两种不同的形式：

基于光谱的GCN（Spectral GCNs）: 基于谱的方法通过从基于图谱理论的图信号处理的角度引入滤波器来定义图卷积。

基于空间的GCN（Spatial GCNs）: 基于空间的方法将图卷积表示为聚合来自邻居的特征信息。

注意：光谱方法的局限性在于所有图样本必须具有相同的结构，即同质结构。但这是一个硬约束，因为大多数现实世界的图数据对于不同的样本具有不同的结构和大小，即异构结构。空间方法与图结构无关。

2.4图卷积神经网络是如何工作的？（How GCNs?）

​ 首先，让我们解决一个朋友预测问题，然后再推广这个方法。

​ __问题陈述：__给你N个人和一张用顶点连接表示其是否为朋友关系的图，你需要判断任意两人在未来是否能成为朋友，例如：

​ 在这里$$(1,2)$$顶点表示1号和2号为朋友关系，相似的有$$(2,3),(3,4),(4,1),(5,6),(6,8),(8,7),(7,6)$$也是朋友关系。

​ 现在想判断我们给出的一对序号代表的人在未来能否成为朋友，比如说我们想探究$$(1,3)$$之间的朋友关系，因为他们都有两个共同好友，我们可以大概猜测出他们有变成朋友的机会，再比如说$$（1,5）$$就没有共同好友，所以他们几乎没有可能成为朋友。

​ 换一个例子:

​ 在上图中$$(1,11)$$成为好朋友的概率要远远高出$$(3,11)$$，那么如何实现上述说明的结果呢？GCN用了一种类似CNN的方法来实现。在卷积神经网络（CNN）中，我们在图像上使用了一个过滤器来获取其在下一层的表示，相似的我们在图卷积神经网络中也使用过滤器来表示下一层特征。

​ 我们把上述描述过程定义成数学公式：$$H^i=f(H^{i-1},A)$$

​ 关于函数$$f$$最简单的例子就是：$$f(H^i,A)=\sigma (A{H}^i{W}^i)$$，其中$$A$$代表了$$N\times N$$的邻接矩阵，$$X$$是$$N\times F$$的输入数据，其中$$N$$代表了结点个数，$$F$$代表了每个输入结点的特征，$$\sigma$$在GCN中为Relu激活函数，第0层的特征值$$H^i$$等于输入数据$$X$$,第$$i$$层的特征矩阵对应于一个$$N\times F^i$$的矩阵（每一行表示每个特征代表的结点），$$f$$就是函数映射。

​ 每一层的特征用规则$$f$$来聚合成下一层的特征，这样特征在接下来的层就会变得更加抽象，这样，我们就有了可以在图上传播信息的功能，可以以半监督的方式进行训练。使用 GCN 层，每个结点（每一行）的表示现在是其邻居特征的总和，换句话说，该层将每个结点表示为其邻域的聚合。

​ __就这么简单么？__停下来仔细想想，我们刚才定义的函数正确么？不正确的，因为他会导致很多问题出现：

​ 1、**某个结点在下一层的新特征不包含它自己之前的特征：**我们可以注意到，如果只使用邻居结点那么它自己的特征就不参与运算，这就会导致结点丢失自己的特征，为了解决上述问题，我们可以在邻接矩阵中加入单位矩阵，这样就相当于在每个顶点上增加了起始和结尾均为自己的结点，这样，”结点也变成了自己的结点“。

​ 2、结点的度数值在图上进行了不对称的缩放：简而言之，具有大量邻居（更高程度）的结点将从相邻结点以邻域聚合的形式获得更多输入，因此将具有更大的值，反之亦然，对于具有较小程度的结点来说可能是正确的小的值，这将会在训练中产生大量的问题。为了解决这个问题，我们将使用标准化，例如归一化 矩阵$$A$$ 使得所有行总和为 1，即 $$D^{-1}A$$，其中$$D$$是对角节点度矩阵，可以解决这个问题，现在乘以$$D^{-1}A$$ 对应于取相邻节点特征的平均值。根据作者，在观测到一些经验的结果后，他们建议”在实际中，当我们使用对称归一化时，例如 ${\hat{D}}^{-\frac{1}{2}}\hat{A}{\hat{D}}^{-\frac{1}{2}}$结果表现得更好。”因为这不再是仅仅对邻居节点的平均了。

​ 通过对上述两种问题解决的陈述，一个新的函数映射可以被定义成以下形式：
$$f(H^{(l)},A)=\sigma \left({\hat{D}}^{-\frac{1}{2}}\hat{A}{\hat{D}}^{-\frac{1}{2}}{H}^{(l)}{W}^{(l)}\right)$$
​ 上述公式中：

​ $$\hat{A}=A+I$$:$$\hat{A}$$表示邻接矩阵加上单位矩阵，其中$$I$$代表单位矩阵。

​ $$\hat{D}$$代表$$\hat{A}$$的度数矩阵。

​

3、Pytoch实现图卷积神经网络

​ 今天我们计划在Zachary Karate Club数据集上使用半监督学习来实现图卷积神经网络，具体使用的算法参考文献：Thomas Kipf and Max Welling.

3.1 Zachary Karate Club数据集介绍

​ 在 1970-1972 年期间，Wayne W. Zachary 观察了当地空手道俱乐部的人。他将这些人表示为图表中的节点，并在两个人之间添加一条边（如果他们相互交互）。结果如下图所示。

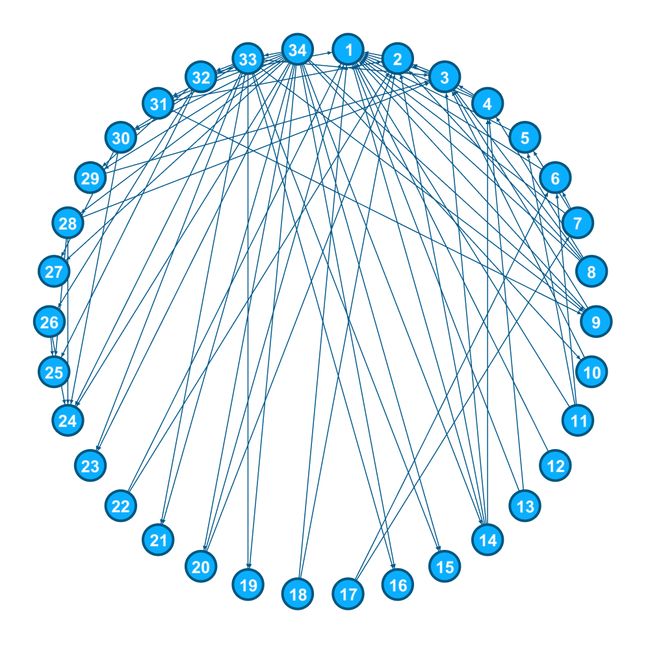
​ 在研究过程中，发生了一件有趣的事情。管理员“John A”和指导员“Mr.Hi”导致了俱乐部一分为二。半数成员围绕Hi先生成立了新俱乐部；另一方的成员找到了新的教练或放弃了空手道。使用他之前找到的图表，他试图预测哪个成员会去哪一半。令人惊讶的是，他能够预测所有成员的决定，除了节点 9 去了Mr. Hi那里而非 John A那里。在这里，我们将使用半监督图学习方法。半监督意味着我们只有一些节点的标签，我们必须找到其他节点的标签。就像在这个例子中一样，我们只有属于“John A”和“Mr.Hi”的节点的标签,我们没有得到任何其他成员的标签，我们只能根据给我们的图表来预测。

3.2必要的导入（Required Imports）

​ 在这篇文章中我们会用到Pytorch和Matploylib

import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt
import imageio

3.3卷积层（The Convolutional Layer）

​ 首先，我们创建一个图卷积类（the Layer creation class）来作为图层创建类。每一个该类的实例都需要传入邻接矩阵类型的输入然后输出$$RELU(A_{h}at\ast X\ast W)$$

class GCNConv(nn.Module):
    def __init__(self, A, in_channels, out_channels):
        super(GCNConv, self).__init__()
        self.A_hat = A+torch.eye(A.size(0))
        self.D     = torch.diag(torch.sum(A,1))
        self.D     = self.D.inverse().sqrt()
        self.A_hat = torch.mm(torch.mm(self.D, self.A_hat), self.D)
        self.W     = nn.Parameter(torch.rand(in_channels,out_channels))
    
    def forward(self, X):
        out = torch.relu(torch.mm(torch.mm(self.A_hat, X), self.W))
        return out

class Net(torch.nn.Module):
    def __init__(self,A, nfeat, nhid, nout):
        super(Net, self).__init__()
        self.conv1 = GCNConv(A,nfeat, nhid)
        self.conv2 = GCNConv(A,nhid, nout)
        
    def forward(self,X):
        H  = self.conv1(X)
        H2 = self.conv2(H)
        return H2

torch.diag(input)取矩阵的对角线元素

torch.sum(input,dtype) dtype=0是按行求和，dtype=1是按列求和

torch.inverse(input)取方阵input的逆矩阵

torch.sqrt(input)逐行计算张量的平方根

# 'A' is the adjacency matrix, it contains 1 at a position (i,j)
# if there is a edge between the node i and node j.
A = torch.Tensor([[0,1,1,1,1,1,1,1,1,0,1,1,1,1,0,0,0,1,0,1,0,1,0,0,0,0,0,0,0,0,0,1,0,0],
                [1,0,1,1,0,0,0,1,0,0,0,0,0,1,0,0,0,1,0,1,0,1,0,0,0,0,0,0,0,0,1,0,0,0],
                [1,1,0,1,0,0,0,1,1,1,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,0,0,0,1,0],
                [1,1,1,0,0,0,0,1,0,0,0,0,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],
                [1,0,0,0,0,0,1,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],
                [1,0,0,0,0,0,1,0,0,0,1,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],
                [1,0,0,0,1,1,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],
                [1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],
                [1,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,1,1],
                [0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1],
                [1,0,0,0,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],
                [1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],
                [1,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],
                [1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1],
                [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1],
                [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1],
                [0,0,0,0,0,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],
                [1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],
                [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1],
                [1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1],
                [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1],
                [1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],
                [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1],
                [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,1,0,1,0,0,1,1],
                [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,1,0,0,0,1,0,0],
                [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,0,0,0,0,0,0,1,0,0],
                [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,1],
                [0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,0,0,0,0,0,0,0,0,1],
                [0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,1],
                [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,1,0,0,0,0,0,1,1],
                [0,1,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1],
                [1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,0,0,1,0,0,0,1,1],
                [0,0,1,0,0,0,0,0,1,0,0,0,0,0,1,1,0,0,1,0,1,0,1,1,0,0,0,0,0,1,1,1,0,1],
                [0,0,0,0,0,0,0,0,1,1,0,0,0,1,1,1,0,0,1,1,1,0,1,1,0,0,1,1,1,1,1,1,1,0]
                ])

target=torch.tensor([0,-1,-1,-1, -1, -1, -1, -1,-1,-1,-1,-1, -1, -1, -1, -1,-1,-1,-1,-1, -1, -1, -1, -1,-1,-1,-1,-1, -1, -1, -1, -1,-1,1])

​ 在上面的例子中，我们有管理员（结点1，第一个结点）和指导者（结点34，最后一个结点）的标签，所以只有这两个设置成为特殊的标签（0和1），其它的结点标签均设置为-1（设置为-1的结点在计算损失时将会忽略掉这些节点的预测值）

​ $$X$$是特征矩阵。因为我们没有每个节点的更多特征，我们将会使用One-hot（独热编码）来对应每个节点的下标值。

3.4训练（Training）

X=torch.eye(A.size(0))

# Here we are creating a Network with 10 features
# in the hidden layer and 2 in the output layer.

T=Net(A,X.size(0), 10, 2)

criterion = torch.nn.CrossEntropyLoss(ignore_index=-1)
optimizer = optim.SGD(T.parameters(), lr=0.01, momentum=0.9)

loss=criterion(T(X),target)


# Plot animation using celluloid

fig = plt.figure()
camera = Camera(fig)

for i in range(200):
    optimizer.zero_grad()
    loss=criterion(T(X), target)
    loss.backward()
    optimizer.step()
    l=(T(X));

    plt.scatter(l.detach().numpy()[:,0],l.detach().numpy()[:,1],
        c=[0, 0, 0, 0 ,0 ,0 ,0, 0, 1, 1, 0 ,0, 0, 0, 1 ,1 ,0 ,0
        ,1, 0, 1, 0 ,1 ,1, 1, 1, 1 ,1 ,1, 1, 1, 1, 1, 1 ])
    
    for i in range(l.shape[0]):
        text_plot = plt.text(l[i,0], l[i,1], str(i+1))

    camera.snap()

    if i%20==0:
        print("Cross Entropy Loss: =", loss.item())

animation = camera.animate(blit=False, interval=150)
animation.save('./train_karate_animation.mp4', writer='ffmpeg', fps=60)
HTML(animation.to_html5_video())

torch.eye(n)：生成对角线全为1，其余部分全为0的二维张量

​ 如你所见，算法将数据分成了两类，并且结果和真实数据十分相似。

3.5 PyG实现

​ 我们也通过PyG库实现了GCNs，PyG是为Pytorch爱好者实现的一个快速测试各类图表征学习算法的库。

​ 下面将通过使用Cora数据集并结合PyG来实现GCNs。

​ 与普通Pytorch版本实现几乎一致，但在PyG中我们通过使用邻接表来代替邻接矩阵。使用邻接表的优势是用边存储复杂度更低，且适用于稀疏图。（在PyG中，用顶点之间关系的邻接表来构图）

​ 如果要调整邻接矩阵为邻接表，那么数学公式也要发生变换。不过，转换是非常简单地。

​ **图卷积层：**Convolution class处理的是邻接表和特征矩阵来作为下一层的输出。

import torch
import torch.nn.functional as F
from torch_geometric.nn import MessagePassing
from torch_geometric.utils import add_self_loops, degree

class GraphConvolution(MessagePassing):
    def __init__(self, in_channels, out_channels,bias=True, **kwargs):
        super(GraphConvolution, self).__init__(aggr='add', **kwargs)
        self.lin = torch.nn.Linear(in_channels, out_channels,bias=bias)

    def forward(self, x, edge_index):
        edge_index, _ = add_self_loops(edge_index, num_nodes=x.size(0))
        x = self.lin(x)
        return self.propagate(edge_index, size=(x.size(0), x.size(0)), x=x)

    def message(self, x_j, edge_index, size):
        row, col = edge_index
        deg = degree(row, size[0], dtype=x_j.dtype)
        deg_inv_sqrt = deg.pow(-0.5)
        norm = deg_inv_sqrt[row] * deg_inv_sqrt[col]
        return norm.view(-1, 1) * x_j #x_j就是edge_index[row]

    def update(self, aggr_out):
        return aggr_out

1、3个函数的重点理解

• add_self_loops(edge_index,edge_weight=None,fill_value=1,num_nodes=None):参数edge_index是边的索引，edge_weight是边的权重，fill_value是边权重的填充数值，默认为1也就是单位矩阵，num_nodes就是结点的数目。

• degree(index,num_nodes=None,dtype=None):参数index是data.edge_index其中的一行（一共有2行），其代码实现为计算其中每个结点出现的次数，那么就是每个结点的度。在原生实现中使用的是scatter_add函数

• scatter_add_(dim,index,other)->Tensor:dim需要处理的索引维度，index是元素索引，other是元素，例如dim=0那么处理的数据为一维数据，上面的作用就是self[index[i]]=self[index[i]]+other[index[i]]其中$$i$$的范围是索引的长度即可。

  import torch
  from torch_geometric.data import Data
  edge_index = torch.tensor([[0,1,1,2],[1,0,2,1]],dtype=torch.long)
  x = torch.tensor([[-1,2,3],[0,0,1],[1,0,-1]],dtype=torch.float)
  data = Data(x=x, edge_index=edge_index)
  from torch_geometric.utils import add_self_loops,degree
  x,_ = add_self_loops(data.edge_index, num_nodes=data.x.size(0))
  row,col = x
  
  selfx = torch.zeros(len(set(row.numpy())),dtype=torch.float)
  print(selfx)
  out = selfx.new_ones((col.size(0)))
  print(out)
  # realize the degree of each node
  for i in range(col.shape[0]):
      selfx[col[i]] += 1
  print('自己实现的度：',selfx)
  

  

2、$$c_{ij}$$的矩阵计算技巧

#在上面代码中，实现这个计算的是
row,col = edge_index
#计算每个结点的度
deg = degree(row,x.size(0),dtype=x.dtype)
#计算1/sqrt(d_{i})
deg_inv_sqrt = deg.pow(-0.5)
norm = deg_inv_sqrt[row]*deg_inv_sqrt[col]

以下图为例，讲解不添加自连接矩阵（add_self_loops）

其度矩阵（$$D_{ij}=\sum _j{A}_{ij}$$,其中$$A_{ij}$$为邻接矩阵）为：

那么如何计算$$c_{ij}=\frac{1}{\sqrt{d_i{d}_j}}$$，以结点0为例，我们需要计算$$c_{0j}$$其中$$j\in N_0$$,共有$$c_{01}$$、$$c_{02}$$、$$c_{03}$$。可以注意到$$c_{ij}=\frac{1}{\sqrt{d_i{d}_j}}=\frac{1}{\sqrt{d_i}}\times \frac{1}{\sqrt{d_j}}$$为了简化运算，我们先对度矩阵中的每个节点进行运算，首先得到：

也就是

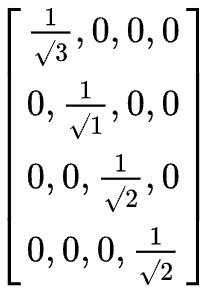
注意在程序中存储的是一维数组，紧接着按照row和col的索引可以直接操作乘法，每个元素按位相乘。