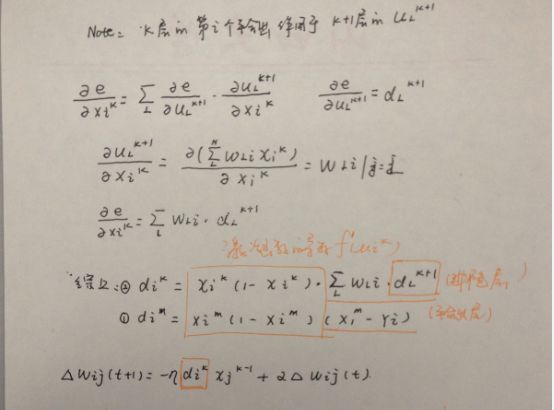神经网络入门学习(一(
人工神经网络
最近,有一篇关于微软亚洲研究院模式识别小组利用残差神经网在2015 ImageNet计算机识别挑战赛中拼接深层神经网最新技术的突破,以绝对的优势获得图像分类。图像定位以及图像检索全部三个项目的冠军,成功的关键就是这个网络丝的深度达到了125层之神(深),我们知道之只包含一层隐含层的神经网络可以训练处大部分连续性函数,随着隐含层个数可以进行无限地逼近理论数值,但是但是,这是理论层次的说明,再实际的应用中会发现的是随着网络层次的增加,我们会发现,网络层次越多,实际的残差会表现的很不明显,也就无法进行更好的学习。残差神经网络就是解决了这方面的问题进而才可以把网络的层次进行最大化的。
深度学习的大力发展和神经网络有着很大的关系,就是让程序自己去学习参数特征,是一种无监督学习,在模式识别,自然语言处理,语音识别有着很大的用处。鉴于如此火爆的神经网络算法的学习,我们来看看神经网络到底是什么。由于CSDN的数学编辑器用不惯,就用手写实现理论的推导。然后基于python实现简只含一个隐藏层的计算。这样的直接用矩阵实现运算。
神经网的python代码实现
这里的函数主要是用来初始化网络的层次结构和权重以及biase的。我们对于这些随机初始化权重和bias用标准的正太扥不来随机初始化。因为,我们这里最终的cost function是基于最小二乘的。sizes=[784, 30, 10])表示每层的神经元的个数,输入的数据是784个神经元,隐含层油30个,输出的结果是10个,因为这里我们需要对手写数字识别进行分类,具体到输入的图像到地址哪个数的概率最大。
class Network(object):
#这里主要是对网络中的权重链接进行初始化
#我们对于这些随机初始化权重和bias用标准的正太扥不来随机初始化
#因为,我们这里最终的cost function是基于最小二乘的。
def __init__(self, sizes):
self.num_layers = len(sizes)#网络的层数
self.sizes = sizes#sizes=[784, 30, 10])表示每层的神经元的个数
#这里的初始化用的是高斯分布
self.biases = [np.random.randn(y, 1) for y in sizes[1:]]
self.weights = [np.random.randn(y, x)
for x, y in zip(sizes[:-1], sizes[1:])]
feedforward函数的作用就是:当网络训练完毕之后,我们需要的是进行对testData进行测试的时候用的函数
def feedforward(self, a):
#zip函数就是把从每一个list中取出一个元素当做tuple处理。
for b, w in zip(self.biases, self.weights):
a = sigmoid(np.dot(w, a)+b)#把每个单元的输出作用于激活函数
return a
SGD函数的主要作用就是模拟了批处理(随机下降),就是每次只是从当前的训练数据集中找不一小部分进行处理。mini_batch_size决定每次处理的数据的大小。有50000个数据,那么有5000次处理,每次10个数据。
def SGD(self, training_data, epochs, mini_batch_size, eta, test_data = None):
if test_data: n_test = len(test_data)
n = len(training_data)
#epochs代表的是迭代的最大次数
for j in xrange(epochs):
#这里的作用是把训练函数随机的打乱。
random.shuffle(training_data)
#进行批处理
mini_batches = [training_data[k:k+mini_batch_size]for k in xrange(0, n, mini_batch_size)]
for mini_batch in mini_batches:
self.update_mini_batch(mini_batch, eta)
if test_data:
print "Epoch {0}: {1} / {2}".format(j, self.evaluate(test_data), n_test)
else:
print "Epoch {0} complete".format(j) update_mini_batch函数的主要作用就是对上面的函数SGD处理的结果进行处理。对每一个训练书进行backprop(x, y)函数处理,这才是最核心的函数。
def update_mini_batch(self, mini_batch, eta):
#nabla_b,nabla_w初始化为0,用来存储更新后的biase和w
nabla_b = [np.zeros(b.shape) for b in self.biases]
nabla_w = [np.zeros(w.shape) for w in self.weights]
for x, y in mini_batch:
#delta_nabla_b, delta_nabla_w变化数值
delta_nabla_b, delta_nabla_w = self.backprop(x, y)
nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
#eta/len(mini_batch)作为学习因子
#这两行主要就是实现对权重和bias的更新
self.weights = [w-(eta/len(mini_batch))*nw for w, nw in zip(self.weights, nabla_w)]
self.biases = [b-(eta/len(mini_batch))*nb for b, nb in zip(self.biases, nabla_b)]最核心的函数
def backprop(self, x, y):
nabla_b = [np.zeros(b.shape) for b in self.biases]
nabla_w = [np.zeros(w.shape) for w in self.weights]
#向前传播
activation = x#轮替的记录每个神经元的输出结果
activations = [x]#记录每个神经元的输出结果
zs = []#记录每个神经元没有经过激活函数的输出结果
for b, w in zip(self.biases, self.weights):
#这里的函数是进行向前传播
#模拟一下。weights应该是有两个矩阵,30*784,10*30的矩阵
#activation中记录的每个神经元的输出结果,一层把输入当做第一层数输出
#是一个784*1,那么w和activation对应点乘就是一个30*1的列向量,经过
#激活函数直接放到第二层作为输入,就可以啦。哈哈
z = np.dot(w, activation)+b
zs.append(z)
activation = sigmoid(z)#轮替的记录每个神经元的输出结果
activations.append(activation)#记录每个神经元的输出结果
# 最关键的地方到了奥
#这里主要计算的是理论的输出和实际输出误差对权重求导的结果
#对应的是上第三章图片上的公式1.cost_derivative是(xi^m-yi)
#sigmoid_prime对应的是(xi^m(1-xi^m))就是激活函数的求导结果
#此时的delta是一个10*1 和 10*1对应元素相乘的结果10*1
delta = self.cost_derivative(activations[-1], y) * sigmoid_prime(zs[-1])
nabla_b[-1] = delta
nabla_w[-1] = np.dot(delta, activations[-2].transpose())
#这儿是对隐藏层的计算
for layer in xrange(2, self.num_layers):
z = zs[-layer]
sp = sigmoid_prime(z)
#对应于第三章图片公式2
#sp就是那个对应于当前层神经元没有经过那个激活函数处理的结果(xi^m(1-xi^m)
#delta对应于dL^k+1就是上一层k+1层对应的求导结果。就是10*1的列阵
#self.weights[-layer+1]就是隐含层到输出层的权重矩阵10*30。
#np.dot(self.weights[-layer+1].transpose(), delta)就是公式2的求和的那部分
#哈哈,讲到这里,我们已经把券代码和公式进行了对应了。
delta = np.dot(self.weights[-layer+1].transpose(), delta) * sp
nabla_b[-layer] = delta
#对应于第三图片的最后一个公式的前半部分。
nabla_w[-layer] = np.dot(delta, activations[-layer-1].transpose())
return (nabla_b, nabla_w)
def evaluate(self, test_data):
test_results = [(np.argmax(self.feedforward(x)), y)
for (x, y) in test_data]
return sum(int(x == y) for (x, y) in test_results)
def cost_derivative(self, output_activations, y):
return output_activations-ydef sigmoid(z):
return 1.0/(1.0+np.exp(-z))
def sigmoid_prime(z):
return sigmoid(z)*(1-sigmoid(z))
if __name__ =="__main__":
training_data, validation_data, test_data = mnist_loader.load_data_wrapper()
net = Network([784, 30, 10])
net.SGD(training_data, 2, 10, 3.0, test_data=test_data)读取数据的辅助函数
import cPickle
import gzip
import numpy as np
def load_data():
f = gzip.open('C:\\Users\\dell\\PycharmProjects\\machineLearing\\neuroNetWork\\mnist.pkl.gz','rb')
training_data, validation_data, test_data = cPickle.load(f)
f.close()
return training_data, validation_data, test_data
def load_data_wrapper():
tr_d, va_d, te_d = load_data()
training_inputs = [np.reshape(x, (784, 1)) for x in tr_d[0]]
training_results = [vectorized_result(y) for y in tr_d[1]]
training_data = zip(training_inputs, training_results)
validation_inputs = [np.reshape(x, (784, 1)) for x in va_d[0]]
validation_data = zip(validation_inputs, va_d[1])
test_inputs = [np.reshape(x, (784, 1)) for x in te_d[0]]
test_data = zip(test_inputs, te_d[1])
return training_data, validation_data, test_data
def vectorized_result(j):
e = np.zeros((10, 1))
e[j] = 1.0
return e
数据放到这里啦, 点击下载