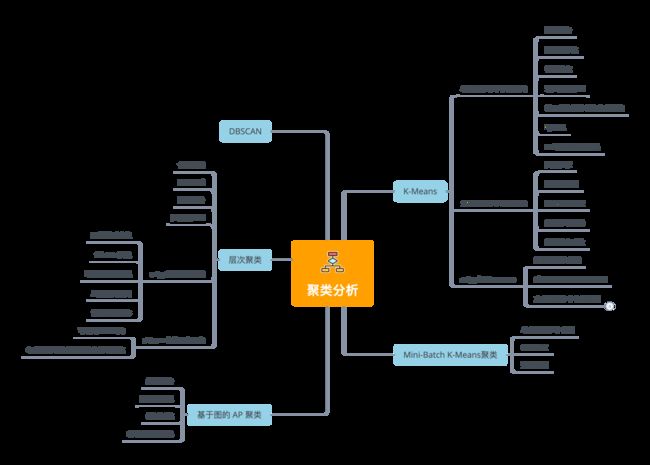
理论+股市数据实战，总结了五种常用聚类分析算法

来源：数据STUDIO

大量数据中具有"相似"特征的数据点或样本划分为一个类别。聚类分析提供了样本集在非监督模式下的类别划分。

基本思想

• 物以类聚、人以群分

常用于数据探索或挖掘前期

• 没有先验经验做探索性分析

• 样本量较大时做预处理

解决问题

• 数据集可以分几类

• 每个类别有多少样本量

• 不同类别中各个变量的强弱关系如何

• 不同类型的典型特征是什么

应用

• 群类别间的差异性特征分析

• 群类别内的关键特征提取

• 图像压缩、分割、图像理解

• 异常检测

• 数据离散化

缺点: 无法提供明确的行动指向; 数据异常对结果有影响。

K-Means 聚类

K-Means算法的思想简单，对于给定的样本集，按照样本之间的距离大小，将样本集划分为K个簇。让簇内的点尽量紧密的连在一起，而让簇间的距离尽量的大。

均值聚类是一种矢量量化方法，起源于信号处理，是数据挖掘中流行的聚类分析方法。

算法原理

• 随机K个质心；

• 开始循环，计算每个样本点到那个质心到距离，样本离哪个近就将该样本分给哪个质心，得到K个簇；

• 对于每个簇，计算所有被分到该簇的样本点的平均距离作为新的质心；

• 直到所有簇不再发生变化。

衡量指标

• 组内平方和：Total_Inertia

• 轮廓系数：  组内差异，组间差异 取值范围越大越好

优化目标

• 内差异小，簇间差异大；其中差异由样本点到其所在簇的质心的距离衡量

应用

• 客户分群、用户画像、精确营销、基于聚类的推荐系统

K-Means算法的优点

• k-means算法是解决聚类问题的一种经典算法，算法简单、快速 。

• 算法尝试找出使平方误差函数值最小的k个划分。当簇是密集的、球状或团状的，且簇与簇之间区别明显时，聚类效果较好 。

缺点

• k-means方法只有在簇的平均值被定义的情况下才能使用，且对有些分类属性的数据不适合。

• 要求用户必须事先给出要生成的簇的数目k。

• 对初值敏感，对于不同的初始值，可能会导致不同的聚类结果。

• 不适合于发现非凸面形状的簇，或者大小差别很大的簇。

• 对于"噪声"和孤立点数据敏感，少量的该类数据能够对平均值产生极大影响。

单支股票单个字段聚类

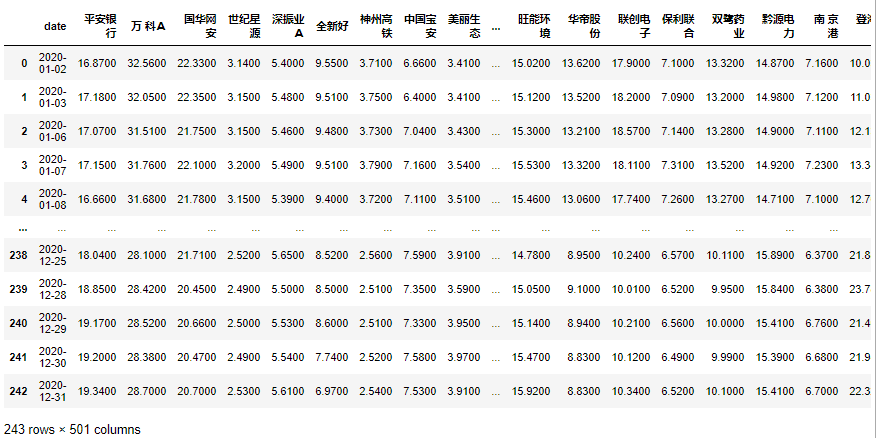
仍然以股市数据为例，根据每支股票整个时间段内的股价特征，将相似的那些交易日打上标签，并通过可视化方式将整个时间段内的交易日开盘价与收盘价展现出来。

数据准备

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings("ignore")
import yfinance as yf
yf.pdr_override()

symbol = 'TCEHY'
start = '2020-01-01'
end = '2021-01-01'

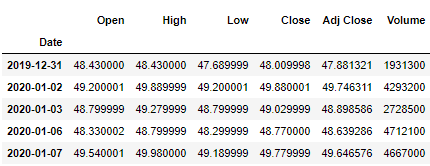
dataset = yf.download(symbol,start,end)
dataset.head()

数据标准化

X = dataset[['Open','High','Low','Close','Adj Close','Volume']]
from sklearn.preprocessing import StandardScaler
X = dataset.values[:,1:]
X = np.nan_to_num(X)
Clus_dataSet = StandardScaler().fit_transform(X)
Clus_dataSet

array([[-1.33493398, -1.31490333, -1.33543485, 
        -1.33612775, -0.95734284],
       [-1.19325204, -1.16643501, -1.15260357, 
        -1.15474442,  0.23740018],
       ...,
       [ 0.99796748,  1.03600566,  0.98270623,  
         0.98235044, -0.41634718],
       [ 1.0222281 ,  0.97701185,  0.99932706,  
         0.99888395, -0.63830968]])

模型建立

from sklearn.cluster import KMeans 
# 设置簇中心个数
clusterNum = 3
k_means = KMeans(init = "k-means++", 
                 n_clusters = clusterNum,
                 n_init = 12)
k_means.fit(X)
labels = k_means.labels_
print(labels)

[1 0 1 0 0 1 1 0...1 1]

设置价格标签

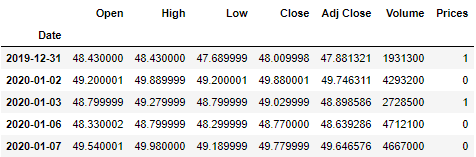
dataset["Prices"] = labels
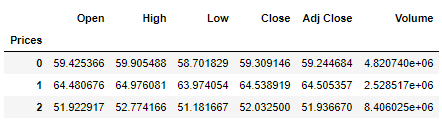
dataset.head(5)

将三个聚类中心聚合求均值

dataset.groupby('Prices').mean()

可视化

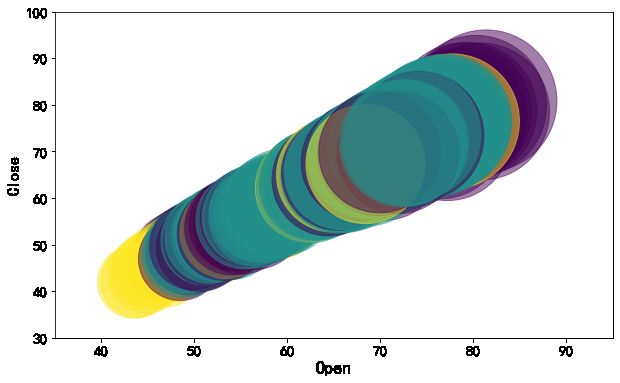
以类别为颜色，开盘价为散点的面积绘制开盘价和收盘价的气泡图。

area = np.pi * ( X[:, 1])**2  
plt.figure(figsize=(10,6))
plt.scatter(X[:, 0], X[:, 3], s=area, 
            c=labels.astype(np.float), 
            alpha=0.5)
plt.xlabel('Open', fontsize=18)
plt.ylabel('Close', fontsize=16)
plt.xticks(fontsize=15)
plt.yticks(fontsize=15)
plt.xlim([35,95])
plt.ylim([30,100])
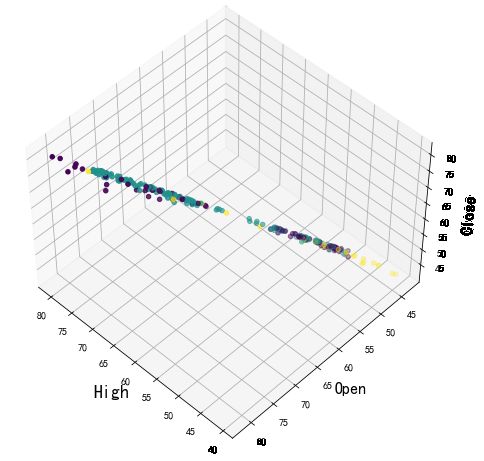
plt.show()

3D可视化聚类结果

from mpl_toolkits.mplot3d import Axes3D 
fig = plt.figure(1, figsize=(8, 6))
plt.clf() # Clear figure
# 设置3d画布
ax = Axes3D(fig, rect=[0, 0, .95, 1], elev=48, azim=134)
plt.cla() # Clear axis
ax.set_xlabel('High', fontsize=18)
ax.set_ylabel('Open', fontsize=16)
ax.set_zlabel('Close', fontsize=16)
# 绘制散点图
ax.scatter(X[:, 1], X[:, 0], X[:, 3], c= labels.astype(np.float))

多支股票单个字段聚类

数据获取

从维基百科中获取股票符号、行业和子行业。

# 美股
wiki_table = pd.read_html('https://en.wikipedia.org/wiki/List_of_S%26P_500_companies',header=0)[0]
symbols = list(wiki_table['Ticker symbol'])
# A股
import urllib
word = '深圳证券交易所主板上市公司列表'
word = urllib.parse.quote(word)
wiki_table = pd.read_html(f'https://zh.wikipedia.org/wiki/{word}',header=0)[0]
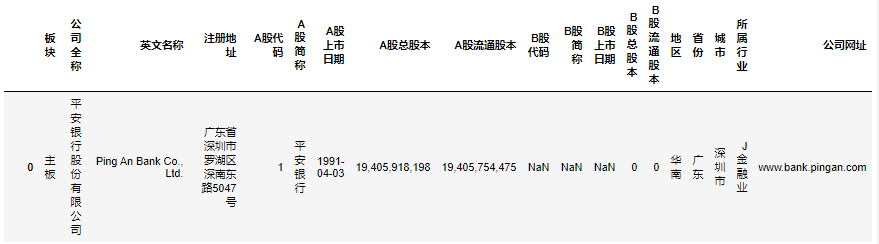
symbols = list(wiki_table['公司代码'])

或直接在深圳证券交易所下载A股列表。

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd 
import baostock as bs
# 从下载下来的A股列上获取上市公司名称及代码
zero = '000000'
A_table = pd.read_excel('./A股列表.xlsx')
A_codes = A_table['A股代码'].map(lambda x: zero[0: 6 - len(str(x))] + str(x))[0: 200].values
A_names = A_table['A股简称'][0: 200].values
print(A_codes)

['000001' '000002' '000004' '000005' '000006' '000007' '000008' '000009'
 '000010' '000011' '000012' '000014' '000016' '000017' '000019' '000020'
  ...
 '000611' '000612' '000613' '000615' '000616' '000617' '000619' '000620'
 '000622' '000623' '000625' '000626' '000627' '000628' '000629' '000630']

根据上面获得的股票代码下载相应日k线图。

bs.login()
dataset = pd.DataFrame()
for num, A_code in enumerate(A_codes):
    print(A_code)
    result = bs.query_history_k_data(A_code, fields = 'date,close',
                                    start_date = '2020-01-01',
                                    end_date = '2021-01-01',
                                    frequency='d')
    df_result = result.get_data().rename(columns={'close':A_names[num]})
    
    if num == 0:
        dataset = df_result
    else:
        dataset = dataset.merge(df_result, on=['date'])
bs.logout()
dataset = dataset.set_index('date').applymap(lambda x: float(x))

数据预处理

import math
# 计算一个理论一年的平均年收益率Returns和波动率Volatility
returns = dataset.pct_change().mean() * 252
returns = pd.DataFrame(returns)
# print(returns)
returns.columns = ['Returns']
returns['Volatility'] = dataset.pct_change(
                    ).std() * math.sqrt(252)
# print(returns['Volatility'])
# 将数据格式化为numpy数组以提供给K-Means算法
data = np.asarray(
          [np.asarray(returns['Returns']),
           np.asarray(returns['Volatility'])]
           ).T
# 删除NaN值，将其替换为0
cleaned_data = np.where(np.isnan(data), 0, data)
X = cleaned_data

建立聚类模型

from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler

# 在变量“n_clusters”中定义集群数量
n_clusters = 12

# 数据聚类
kmeans = KMeans(n_clusters)
kmeans.fit(X)

KMeans(algorithm='auto', copy_x=True, init='k-means++', max_iter=300,
    n_clusters=12, n_init=10, n_jobs=None, precompute_distances='auto',
    random_state=None, tol=0.0001, verbose=0)

绘制学习曲线

from sklearn.cluster import KMeans

min_clusters = 1
max_clusters = 20
distortions = []
for i in range(min_clusters, max_clusters+1):
    km = KMeans(n_clusters=i,
                init='k-means++',
                n_init=10,
                max_iter=300,
                random_state=0)
    km.fit(X)
    distortions.append(km.inertia_)
    
# 绘图
plt.figure(figsize=(14,6))
plt.plot(range(min_clusters, max_clusters+1), distortions, marker='o')
plt.xlabel("Number of clusters", fontsize=18)
plt.ylabel("Distortion", fontsize=16)
plt.xticks(fontsize=15)
plt.yticks(fontsize=15)
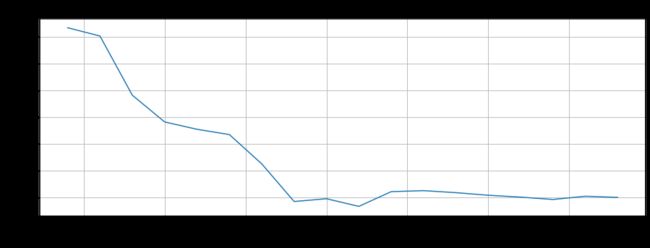
plt.show()

绘制轮廓系数

wcss = []
from sklearn.metrics import silhouette_score
for k in range(2, 20):
    k_means = KMeans(n_clusters=k)
    k_means.fit(X)
    wcss.append(silhouette_score(X, k_means.labels_))
fig = plt.figure(figsize=(15, 5))
plt.plot(range(2, 20), wcss)
plt.grid(True)
plt.xticks(fontsize=15)
plt.xlabel("Number of clusters", fontsize=18)
plt.ylabel('Silhouette_score', fontsize=15)
plt.title('Silhouette_score curve', fontsize=18)
plt.show()

简单判断下，图中拐点位置大致在聚类中心个数为9时，此时轮廓系数最小。则n_clusters可以选择等于9.

scipy中的k-means

from scipy.cluster.vq import kmeans, vq
# 计算 K = 5 的K均值(5个簇)
centroids,_ = kmeans(cleaned_data,5)
# 将每个样本分配给一个簇
idx,_ = vq(cleaned_data,centroids)
data = cleaned_data

绘制聚类散点图

将每种簇按照不同的颜色区分绘制，同时绘制出簇中心。

统计每个股票属于哪个簇

details = [(name,cluster) for name, 
          cluster in zip(returns.index,idx)]
labels =['A股简称', 'Cluster']
df = pd.DataFrame.from_records(details, 
                               columns=labels)
df.head(n=10)

	A股简称	Cluster
0	平安银行	3
1	万 科Ａ	1
2	国华网安	3
3	世纪星源	1
4	深振业Ａ	3
5	全新好	2
6	神州高铁	2
7	中国宝安	3
8	美丽生态	3
9	深物业A	0

‍

‍多支股票多个字段举例

stocks_dict = dict(zip(A_names,A_codes))
bs.login()
dataset = []
for names, A_code in stocks_dict.items():
    print(A_code)
    result = bs.query_history_k_data(A_code, fields = 'date,open,high,low,close,volume',
                                    start_date = '2020-01-01',
                                    end_date = '2021-01-01',
                                    frequency='d')
    df_result = result.get_data()
    dataset.append(df_result)
bs.logout()

# 获取开盘价
open_price = np.array([p["open"] for p in dataset]).astype(np.float)

# 获取收盘价
close_price = np.array([p["close"] for p in dataset]).astype(np.float)
# 计算变化率
X = (close_price - open_price) / open_price

建模

from sklearn.cluster import KMeans
# 定义聚类中心个数
n_clusters = 12
kmeans = KMeans(n_clusters)
kmeans.fit(X)
# 输出结果
labels = kmeans.labels_
for i in range(n_clusters):
    print('Cluster %i: %s' % ((i + 1), 
          ', '.join(A_names[labels == i])))

使用管道链接归一化和聚类模型

from sklearn.pipeline import make_pipeline
from sklearn.cluster import KMeans
from sklearn.preprocessing import Normalizer

normalizer = Normalizer()
kmeans = KMeans(n_clusters=10, max_iter = 1000)
# 制作一个管道链接归一化和kmeans
pipeline = make_pipeline(normalizer, kmeans)
pipeline.fit(X)
labels = pipeline.predict(X)
df = pd.DataFrame({'labels':labels,
                   'companies':A_names})
print(df.sort_values('labels'))

labels companies
434       0      华铁股份
472       0      协鑫能科
419       0      首钢股份
417       0      中通客车
194       0      长安汽车
..      ...       ...
266       9      鲁  泰Ａ
268       9      国元证券
467       9      传化智联
234       9      中山公用
0         9      平安银行

[500 rows x 2 columns]

使用PCA降维

如果用于聚类的数据维度很高，在使用聚类分析时通常会占用过程的计算时间。此时运用PCAj降维方法。

from sklearn.preprocessing import Normalizer
from sklearn.decomposition import PCA
normalizer = Normalizer()
new_X = normalizer.fit_transform(X)
# 使用PCA降维
reduced_data = PCA(n_components = 2).fit_transform(new_X)
#对降维后的数据训练kmeans
kmeans = KMeans(n_clusters =10)
kmeans.fit(reduced_data)
labels = kmeans.predict(reduced_data)
# print(kmeans.inertia_)
# 创建DataFrame
df = pd.DataFrame({'labels':labels,
                   'companies':A_names})
# 根据标签排序
print(df.sort_values('labels'))

3.2745576650179067
     labels companies
339       0      *ST长动
445       0      诚志股份
37        0      德赛电池
244       0      模塑科技
41        0      深 赛 格
..      ...       ...
275       9      南风化工
108       9      国际医学
22        9      深深房Ａ
444       9      九 芝 堂
164       9      *ST金洲

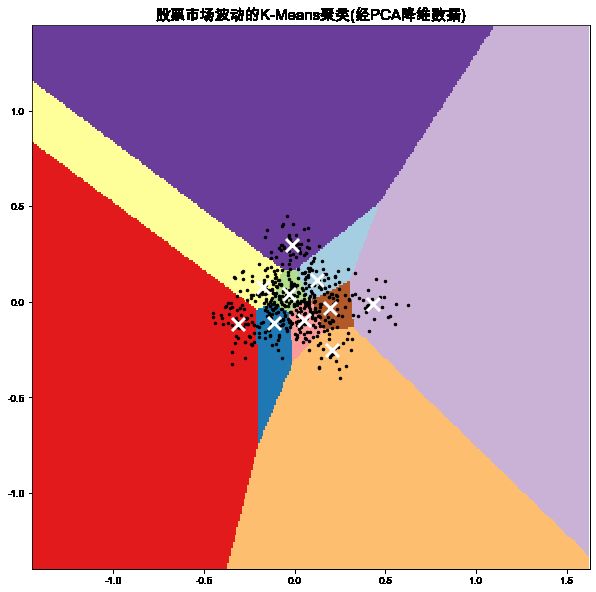
[500 rows x 2 columns]

可视化簇及簇中心

Mini-Batch K-Means聚类

Mini Batch K-Means算法是K-Means算法的变种，采用小批量的数据子集减小计算时间，同时仍试图优化目标函数，这里所谓的小批量是指每次训练算法时所随机抽取的数据子集，采用这些随机产生的子集进行训练算法，大大减小了计算时间，与其他算法相比，减少了K-Means的收敛时间，小批量K-Means产生的结果，一般只略差于标准算法。

该算法的迭代步骤有两步：

• 从数据集中随机抽取一些数据形成小批量，把他们分配给最近的质心

• 更新质心

与K-Means算法相比，数据的更新是在每一个小的样本集上。对于每一个小批量，通过计算平均值得到更新质心，并把小批量里的数据分配给该质心，随着迭代次数的增加，这些质心的变化是逐渐减小的，直到质心稳定或者达到指定的迭代次数，停止计算。

单支股票多个字段

import baostock as bs
bs.login()
result = bs.query_history_k_data('sh.601318', fields = 'date,open,high, low,close,volume',
                                    start_date = '2018-01-01',
                                    end_date = '2021-01-01',
                                    frequency='d')
dataset = result.get_data().set_index('date').applymap(lambda x: float(x))
bs.logout()

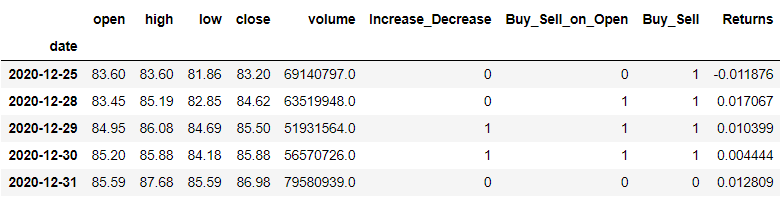
dataset['Increase_Decrease'] = np.where(dataset['volume'].shift(-1) > dataset['volume'],1,0)
dataset['Buy_Sell_on_Open'] = np.where(dataset['open'].shift(-1) > dataset['open'],1,0)
dataset['Buy_Sell'] = np.where(dataset['close'].shift(-1) > dataset['close'],1,0)
dataset['Returns'] = dataset['close'].pct_change()
dataset = dataset.dropna()
dataset.tail()

模型建立

from sklearn.preprocessing import StandardScaler
from sklearn.cluster import MiniBatchKMeans

X = dataset.drop(['close', 'open'], axis=1).values
Y = dataset['close'].values
# 数据标准化
scaler = StandardScaler()
X_std = scaler.fit_transform(X)
# 创建聚类对象
clustering = MiniBatchKMeans(n_clusters=3, random_state=0, batch_size=100)
# 训练模型
model = clustering.fit(X_std)

预测结果

model.cluster_centers_
model.labels_
model.predict(X,Y)

基于图的 AP 聚类

Affinity Propagation Clustering（简称AP算法）特别适合高维、多类数据快速聚类，相比传统的聚类算法，该算法算是比较新的，从聚类性能和效率方面都有大幅度的提升。

AP算法的基本思想：将全部样本看作网络的节点，然后通过网络中各条边的消息传递计算出各样本的聚类中心。聚类过程中，共有两种消息在各节点间传递，分别是吸引度( responsibility)和归属度(availability) 。

AP算法通过迭代过程不断更新每一个点的吸引度和归属度值，直到产生m个高质量的Exemplar（类似于质心），同时将其余的数据点分配到相应的聚类中。

AP算法流程：

• 步骤1：算法初始，将吸引度矩阵R和归属度矩阵初始化为0矩阵；

• 步骤2：更新吸引度矩阵

• 步骤3：更新归属度矩阵

• 步骤4：根据衰减系数  对两个公式进行衰减

• 重复步骤2，3,4直至矩阵稳定或者达到最大迭代次数，算法结束。

• 最终取最大的k作为聚类中心。

AP聚类算法的特点：

• 无需指定聚类“数量”参数。

• 明确的质心（聚类中心点）。

• 对距离矩阵的对称性没要求。

• 初始值不敏感。

• 算法复杂度较高，为 ，为样本数， 为迭代次数，而K-Means只是 的复杂度。

• 若以误差平方和来衡量算法间的优劣，AP聚类比其他方法的误差平方和都要低。

AP算法相对K-Means鲁棒性强且准确度较高，但没有任何一个算法是完美的，AP聚类算法也不例外：

• AP聚类应用中需要手动指定Preference和Damping factor，这其实是原有的聚类“数量”控制的变体。

• 算法较慢。由于AP算法复杂度较高，运行时间相对K-Means长，这会使得尤其在海量数据下运行时耗费的时间很多。

数据准备

market_dates = np.vstack([dataset.index])
open_price = np.array([p["open"] for p in dataset]).astype(np.float)
high_price = np.array([p["high"] for p in dataset]).astype(np.float)
low_price = np.array([p["low"] for p in dataset]).astype(np.float)
close_price = np.array([p["close"] for p in dataset]).astype(np.float)
volume_price = np.array([p["volume"] for p in dataset]).astype(np.float)

数据预处理

# 计算变化率
X = (close_price - open_price) / open_price
# 每日变化的报价是什么携带最多的信息
variation = close_price - open_price
from sklearn import cluster, covariance, manifold, preprocessing
# 从相关性中学习图形结构
edge_model = covariance.GraphicalLassoCV()
# 标准化时间序列:使用相关性而不是协方差
# 是更有效的结构恢复
X = variation.copy().T

# 在对输入数据进行归一化之后，经验协方差矩阵的特征值仍然跨越大约[0-8]的较大范围。
# 使用sklearn.covariance.shrunk_covariance（）函数缩小此范围可以使其在计算上更容易接受
myScaler = preprocessing.StandardScaler()
X = myScaler.fit_transform(X)
emp_cov = covariance.empirical_covariance(X)
shrunk_cov = covariance.shrunk_covariance(emp_cov, shrinkage=0.8)

模型训练

edge_model.fit(shrunk_cov)
# 使用ffinity propagation聚类
_, labels = cluster.affinity_propagation(edge_model.covariance_)
n_labels = labels.max()
for i in range(n_labels + 1):
    print('Cluster %i: %s' % ((i + 1), ', '.join(A_names[labels == i])))

市场结构可视化

算法的基本思想是将样本数据看做网络的节点，根据节点之间的相互关系计算出每个节点作为聚类中心的合适程度，选择合适程度最高的几个数据节点作为聚类中心，并将其他节点分配给最合适的聚类中心。

DBSCAN 聚类

一种基于密度的带有噪声的空间聚类 。它将簇定义为密度相连的点的最大集合，能够把具有足够高密度的区域划分为簇，并可在噪声的空间数据集中发现任意形状的聚类。

基于密度的空间聚类与噪声应用。寻找高密度的核心样本，并从中扩展星团。适用于包含相似密度的簇的数据。

DBSCAN算法将聚类视为由低密度区域分隔的高密度区域。由于这种相当通用的观点，DBSCAN发现的集群可以是任何形状，而k-means假设集群是凸形的。DBSCAN的核心组件是核心样本的概念，即位于高密度区域的样本。因此，一个集群是一组彼此接近的核心样本(通过一定的距离度量)和一组与核心样本相近的非核心样本(但它们本身不是核心样本)。

>>> from sklearn.cluster import DBSCAN
>>> import numpy as np
'''
X = np.array([[1, 2], [2, 2], [2, 3],
              [8, 7], [8, 8], [25, 80]])
'''
>>> clustering = DBSCAN(eps=3, min_samples=2).fit(X)
>>> clustering.labels_
'array([ 0,  0,  0,  1,  1, -1])'
>>> clustering
'DBSCAN(eps=3, min_samples=2)'

eps float, default=0.5 两个样本之间的最大距离，其中一个样本被认为是相邻的。这不是集群内点的距离的最大值，这是为您的数据集和距离函数选择的最重要的DBSCAN参数。

min_samples int, default=5 被视为核心点的某一邻域内的样本数(或总权重)。这包括点本身。

层次聚类

层次聚类（Hierarchical Clustering）在数据挖掘和统计中，层次聚类是一种聚类分析方法，旨在建立一个层次的聚类。

层次聚类(Hierarchical Clustering)通过计算不同类别数据点间的相似度来创建一棵有层次的嵌套聚类树。在聚类树中，不同类别的原始数据点是树的最低层，树的顶层是一个聚类的根节点。创建聚类树有自下而上合并和自上而下分裂两种方法，

合并算法

层次聚类的合并算法通过计算两类数据点间的相似性，对所有数据点中最为相似的两个数据点进行组合，并反复迭代这一过程。

简单来说

通过计算每一个类别的数据点与所有数据点之间的欧式距离来确定它们之间的相似性，距离越小，相似度越高 。并将距离最近的两个数据点或类别进行组合，生成聚类树。

数据准备

import baostock as bs
bs.login()
result = bs.query_history_k_data('sh.601318', fields = 'date,open,high, low,close,volume',
                                    start_date = '2017-01-01',
                                    end_date = '2021-01-01',
                                    frequency='d')
dataset = result.get_data().set_index('date').applymap(lambda x: float(x))
bs.logout()
dataset = dataset.dropna()
dataset = dataset.reset_index(drop=True)
print("Shape of dataset after cleaning: ", dataset.size)
dataset.head(5)

Shape of dataset after cleaning:  4870

数据预处理

features = dataset[['open','high','low','close','volume']]
# 标准化
# 将每个数据缩放到0和1之间
from sklearn.preprocessing import MinMaxScaler
x = features.values #returns a numpy array
min_max_scaler = MinMaxScaler()
feature_mtx = min_max_scaler.fit_transform(x)
feature_mtx [0:5]

array([[0.00189166, 0.00996622, 0.00734394,  
        0.00807977, 0.04191282],
       [0.00791058, 0.00625   , 0.0106662 , 
        0.00756404, 0.02496157],
       [0.00859845, 0.00878378, 0.01363875, 
        0.00893932, 0.03806948],
       [0.00859845, 0.00793919, 0.00786851, 
        0.00395393, 0.06706422],
       [0.00412726, 0.00219595, 0.00646966, 
        0.00361011, 0.03184948]])

scipy中的层次聚类

聚类模型建立

• criterion='distance'

import scipy
leng = feature_mtx.shape[0]
D = np.zeros([leng,leng])
for i in range(leng):
    for j in range(leng):
        # 计算两个一维数组之间的欧氏距离。
        # scipy.spatial.distance中包含各种距离的计算
        D[i,j] = scipy.spatial.distance.euclidean(feature_mtx[i], feature_mtx[j])
        
from scipy.cluster import hierarchy 
from scipy.cluster.hierarchy import fcluster

Z = hierarchy.linkage(D, 'complete')
max_d = 3
clusters = fcluster(Z, max_d, criterion='distance')
clusters

array([43, 43, 43, 43, 43, 43, 43, 43, 43, 
       44, 43, 43, 43, 43, 43, 43, 43,
       43, 43, 45, 43, 43, 43, 43, 45, 43, 
       45, 43, 45, 45, 45, 45, 45, 43,
        ...
       30, 30, 30, 30, 32, 32, 30, 28, 28, 
       28, 28, 28, 38, 38, 36, 34, 33,
       33, 33, 33, 36, 36, 37, 37, 38, 37, 
       28, 37, 37, 37, 37, 28, 27, 27,
       30, 27, 28, 28, 28], dtype=int32)

• criterion='maxclust'

from scipy.cluster.hierarchy import fcluster
k = 5
clusters = fcluster(Z, k, criterion='maxclust')
clusters

array([4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4,
       4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4,
       ...
       2, 2, 2, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2], dtype=int32)

fcluster参数

scipy.cluster.hierarchy.fcluster(Z,    
                    t, 
                    criterion='inconsistent', 
                    depth=2, 
                    R=None, 
                    monocrit=None)

Z: ndarray

根据给定的链接矩阵定义的层次聚类，形成平面聚类。

t: scalar

• 对于 "inconsistent", "distance "or "monocrit" 的标准，这是形成平面集群时要应用的阈值。

• 对于"maxclust"或"maxclust_monocrit"标准，这将是请求的最大集群数量。

criterion: str 可选参数
用于形成扁平集群的标准。可以是以下任何值：

• inconsistent:

如果一个集群节点及其所有后代节点的值小于或等于t的值不一致，那么它的所有叶子后代都属于同一个平面集群。当没有非单例集群满足此条件时，每个节点都被分配到自己的集群中。(默认)

• distance:

形成扁平的群集，使每个平面集群的原始观测结果不大于同聚距离。

• maxclust:

求一个最小阈值，使同一平面集群中任意两个原始观测之间的同聚距离不大于且不超过个聚类形成的平面集群

• monocrit:

当monocrit[j] <= t时，从索引为i的簇节点c形成一个扁平集群

例如，对不一致矩阵R中计算的最大平均距离阈值设为0.8的阈值:

MR = maxRstat(Z, R, 3)
fcluster(Z, t=0.8, criterion='monocrit', monocrit=MR)

• maxclust_monocrit:

当下面和包括的所有集群指数时，从非单子集群节点形成一个扁平的集群。最小化，以至于形成不超过扁平的集群。单节必须是单调的。例如，要最大限度地降低最大不一致值上的阈值 t，以便形成不超过 3 个平面集群，则需要：

从一个非单例集群节点形成一个平面集群时，所有的集群索引都被最小化，这样只会形成一个平面集群。monocrit 必须是单调的。

例如，要最小化最大不一致性值的阈值t，以便形成不超过3个平面集群，请执行:cmonocrit[i] <= ricrt

MI = maxinconsts(Z, R)
fcluster(Z, t=3, criterion='maxclust_monocrit', monocrit=MI)

可视化层次聚类

import pylab
fig = pylab.figure(figsize=(18,50))
def llf(id):
    return '[%s %s %s]' % (dataset['high'][id], dataset['low'][id], int(float(dataset['close'][id])) )
    
dendro = hierarchy.dendrogram(Z,  leaf_label_func=llf, leaf_rotation=0, leaf_font_size =12, orientation = 'right')

pylab 提供了比较强大的画图功能，平常使用最多的应该是画线了。

hierarchy.dendrogram将分层聚类绘制为树状图。

树状图通过在非单例群集及其子级之间绘制一条U-shaped链接来说明每个群集的组成方式。U-link的顶部指示群集合并。U-link的两条腿指示要合并的集群。U-link的两条腿的长度表示子群集之间的距离。它也是两个子类中原始观测值之间的距离。

Z: ndarray

链接矩阵编码分层聚类以呈现为树状图。看到linkage函数以获取有关格式的更多信息Z。

orientation：str, 可选参数
树状图的绘制方向，可以是以下任意字符串：

• 'top'

在顶部绘制根，并绘制向下的后代链接。(默认)。

• 'bottom'

在底部绘制根，并绘制向上的后代链接。

• 'left'

在左边绘制根，在右边绘制后代链接。

• 'right'

在右边绘制根，在左边绘制后代链接。

leaf_rotation：double, 可选参数
指定旋转叶子标签的角度(以度为单位)。如果未指定，则旋转基于树状图中的节点数(默认为0)。

leaf_font_size：int, 可选参数
指定叶子标签的字体大小(以磅为单位)。未指定时，大小基于树状图中的节点数。

leaf_label_func：lambda 或 function, 可选参数
当leaf_label_func是可调用函数时，对于具有簇索引的每个叶子。该函数应返回带有叶子标签的字符串。

指标  对应于原始观察值，而索引对应于非单簇。

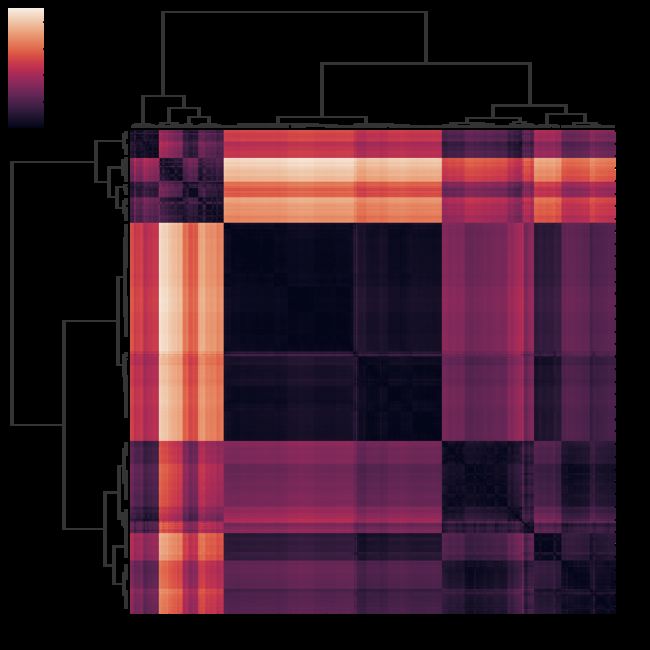
层次聚类热图

热图的绘制非常简单，因为seaborn的工具包非常强大，我们使用clustermap函数即可。

import seaborn as sns
sns.clustermap(D,method ='ward',metric='euclidean')

1

计算距离矩阵

from scipy.spatial import distance_matrix 
# 返回所有成对距离的矩阵。
dist_matrix = distance_matrix(feature_mtx,feature_mtx) 
print(dist_matrix)

[[0.         0.01867314 0.01007541 ... 1.71146908 
  1.71172797 1.75931251]
 [0.01867314 0.         0.01376365 ... 1.70982933 
  1.71026084 1.75873221]
 ...
 [1.71172797 1.71026084 1.70562427 ... 0.02158105 
  0.         0.09823995]
 [1.75931251 1.75873221 1.75346407 ... 0.11352427 
  0.09823995 0.        ]]

sklearn中的层次聚类

from sklearn.cluster import AgglomerativeClustering 
agglom = AgglomerativeClustering(n_clusters = 6, linkage = 'complete')
agglom.fit(feature_mtx)
agglom.labels_

array([3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 
       3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3,
       3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 
       3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3,
     ...
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2], dtype=int64)

dataset['cluster_'] = agglom.labels_
dataset.head()

可视化层次聚类

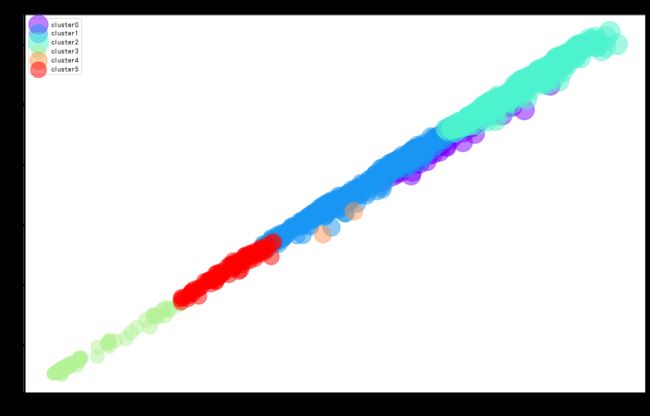
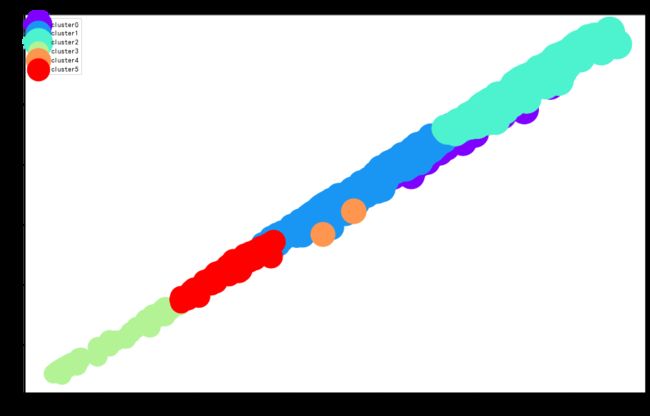
分别以股票的最高价和最低价为轴，以收盘价为圆圈的面积，以不同颜色区分不同簇，绘制聚类散点图。

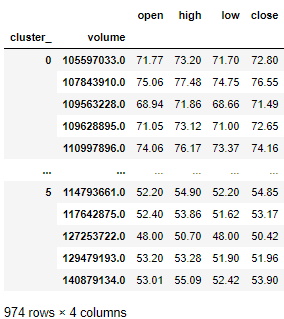
每个集群中按交易量聚合并可视化

agg_price = dataset.groupby(['cluster_','volume'])['open','high','low','close'].mean()
agg_price

同样以股票的最高价和最低价为轴，以收盘价为圆圈的面积，以不同颜色区分不同簇，绘制聚类散点图。

---------End---------

顺便给大家推荐下我的微信视频号「Python数据之道」，欢迎扫码关注。