运筹学 | 线性规划求解算法 | 单纯形法的python实现
单纯形法是在线性规划可行域的顶点中搜索最优解的算法,可以被分为三个步骤:
- 找到顶点
- 搜索顶点
- 判断在某顶点处是否最优
如何找到可行域的顶点?
- 存在由线性等式和不等式构成的多面体 P = { X ∈ R n ∣ ∑ j = 1 n P j x j = b , X ≥ 0 } P = \{X \in R^n | \sum_{j=1}^n P_jx_j = \boldsymbol b, X\geq \boldsymbol 0 \} P={X∈Rn∣∑j=1nPjxj=b,X≥0} ,若X是一个基本解且满足所有约束条件,则称X是一个基本可行解.
- 线性规划的基可行解对应可行域的顶点
也就是说,顶点需要满足所有等式约束,即 X ∈ { R n ∣ ∑ j = 1 n P j x j = b , X ≥ 0 } X \in \{ R^n | \sum_{j=1}^n P_jx_j = \boldsymbol b, X\geq \boldsymbol 0 \} X∈{Rn∣∑j=1nPjxj=b,X≥0},其中由于 ∑ j = 1 n P j x j = b \sum_{j=1}^n P_jx_j = \boldsymbol b ∑j=1nPjxj=b 只有 m m m行, m < n m
关于如何判定X是否为基解的证明这里不再赘述,具体可以参考线性规划中的几何(二)极点、顶点和基本可行解。
如何搜索顶点?
单纯形法的搜索过程是沿着相邻顶点移动的。
相邻顶点的判断依据为: 决定两个顶点的约束(紧的那种)集合中只有一个约束不同,则这两个顶点相邻。根据顶点的定义,这个不同的约束便是剩下n-m解满足的等于0的约束。
搜索顶点的部分便对应着单纯形法中变量进基、出基的变换。
如何判断是否最优?
值得注意的是,在单纯形法无法体现线性规划问题无可行解的情况,只能判断是否为唯一最优解、无穷多最优解、无界解的情况。若需要加入无可行解的判断,可以考虑采用大M法和两阶段法,通过判断是否有不为零的人工变量,来确定线性规划解的情况。
单纯形法的python实现
这里的单纯形法要求输入线性规划的标准形式,即目标函数求最大值,约束为等式,所有变量具有非负性。
不同教程对线性规划的标准形式定义不同,例如,陈宝林编著的《最优化理论与算法》的标准形式定义里,目标函数是求最小值。
class Simplex:
def __init__(self) -> None:
self.solutionStatus = 0
def set_param(self, A, b, c, baseInd):
self.A = A
self.m, self.n = self.A.shape
self.b = b
self.c = c
self.baseInd = baseInd
self.nonbaseInd = [i for i in range(self.n) if i not in self.baseInd]
self.B = self.A[:, self.baseInd]
self.N = self.A[:, self.nonbaseInd]
self.B_inv = self.B.I
def main(self):
# 计算非基变量的检验数,基变量检验数为0
reducedCost = [0] * self.n
X_B = None
simplexTable = SimplexTable()
while (self.solutionStatus == 0):
for i in range(self.n):
reducedCost[i] = float(self.c[:, i] - np.dot(self.c[:, self.baseInd], self.A[:, i]))
# p_j已经全部左乘B_inv,因此这里c_B可以直接与更新后的p_j相乘
self.solutionStatus = self.check_solutionStatus(reducedCost)
simplexTable.show(self.A,self.b,self.c,reducedCost,self.baseInd,self.solutionStatus)
if self.solutionStatus == 0:
inVarInd = reducedCost.index(max(reducedCost))
outVarInd = self.get_outVar(inVarInd)
self.baseInd[self.baseInd.index(outVarInd)] = inVarInd
self.nonbaseInd[self.nonbaseInd.index(inVarInd)] = outVarInd
# 得到新基
self.B = self.A[:, self.baseInd]
self.B_inv = self.B.I
self.b = np.dot(self.B_inv, self.b)
X_B = self.b.T.tolist()[0]
self.A[:, inVarInd] = self.A[:, outVarInd]
self.A[:, self.nonbaseInd] = np.dot(self.B_inv, self.A[:, self.nonbaseInd])
else:
break
if self.solutionStatus == 1:
solution = {}
for i in range(self.n):
if i in self.baseInd:
solution[i] = X_B[self.baseInd.index(i)]
if i in self.nonbaseInd:
solution[i] = 0
objctive = float(np.dot(np.dot(self.c[:, self.baseInd], self.B_inv), self.b))
return solution, objctive, self.solutionStatus
else:
solution = None
objctive = None
return solution, objctive, self.solutionStatus
def check_solutionStatus(self, reducedCost):
if all(x < 0 or x == 0 for x in reducedCost):
# 所有检验数<=0
if any(reducedCost[i] == 0 for i in self.nonbaseInd):
# 存在非基变量的检验数为0
return 2 # 无穷多最优解
else:
return 1 # 唯一最优解
else:
if all(all(x < 0 for x in self.A[:, i]) for i in self.nonbaseInd if reducedCost[i] > 0):
return 3 # 无界解
else:
# 选择最大检验数对应的非基变量入基
return 0
def get_outVar(self, inVarInd):
inVarCoef = self.A[:, inVarInd]
ratio = [np.inf] * self.m
for i in range(len(inVarCoef)):
if float(inVarCoef[i, :]) > 0:
ratio[i] = float(self.b[i, :]) / float(inVarCoef[i, :])
outVarInd = self.baseInd[ratio.index(min(ratio))]
return outVarInd
打印单纯形表获得更直观的算法迭代过程:
class SimplexTable:
def __init__(self):
# 左端表头格式设置
self.setting_left = '{:^8}'+'{:^8}'+'{:^8}|'
# 右端变量格式设置
self.setting_var = '{:^8}|'
# 求解状态格式设置
self.setting_status = '{:^24}|'+'{:^44}|'
def show(self,A,b,c,reducedCost,baseInd,solutionStatus):
var_num = A.shape[1]
# 打印系数行
c_j_list = c.flatten().tolist()[0]
print(self.setting_left.format('','c_j',''),end = '')
for i in c_j_list:
print(self.setting_var.format(i),end = '')
print()
# 打印变量行
print(self.setting_left.format('c_B','x_B','b'),end = '')
for i in range(var_num):
print(self.setting_var.format('x'+str(i)),end = '')
print()
# 打印变量与矩阵
for i in range(len(baseInd)):
varInd = baseInd[i]
varCeof = round(float(c[:,varInd]),2)
varValue = round(float(b[i,:]),2)
row = A[i,:].flatten().tolist()[0]
print(self.setting_left.format(str(varCeof),'x'+str(varInd),str(varValue)),end='')
for i in range(var_num):
print(self.setting_var.format(round(row[i],2)),end = '')
print()
# 打印检验数
print(self.setting_left.format('','c_j-z_j',''),end='')
for i in reducedCost:
print(self.setting_var.format(round(i,2)),end = '')
print()
# 显示求解状态
if solutionStatus == 0:
print(self.setting_status.format('status','...Iteration continues...'))
if solutionStatus == 1:
print(self.setting_status.format('status','Unique Optimal Solution'))
B = A[:,baseInd]
B_inv = B.I
objctive = float(np.dot(np.dot(c[:, baseInd], B_inv), b))
print(self.setting_status.format('objctive', round(objctive,2)))
solution = [0]*var_num
X_B = b.T.tolist()[0]
for i in range(var_num):
if i in baseInd:
solution[i] = X_B[baseInd.index(i)]
print(self.setting_left.format('', 'solution', ''), end='')
for i in solution:
print(self.setting_var.format(round(i, 2)), end='')
print()
if solutionStatus == 2:
print(self.setting_status.format('status','Multiple Optimal Solutions'))
B = A[:, baseInd]
B_inv = B.I
objctive = float(np.dot(np.dot(c[:, baseInd], B_inv), b))
print(self.setting_status.format('objctive', round(objctive, 2)))
if solutionStatus == 3:
print(self.setting_status.format('status','Unboundedness'))
算例测试
case 1 : Unique Optimal Solution
A = np.matrix([[1, 1, -2, 1, 0, 0],
[2, -1, 4, 0, 1, 0],
[-1, 2, -4, 0, 0, 1]], dtype=np.float64)
# 必须设置精度,否则在替换矩阵列时会被自动圆整
b = np.matrix([[10], [8], [4]], dtype=np.float64)
c = np.matrix([-1, 2, -1, 0, 0, 0], dtype=np.float64)
baseInd = [3, 4, 5]
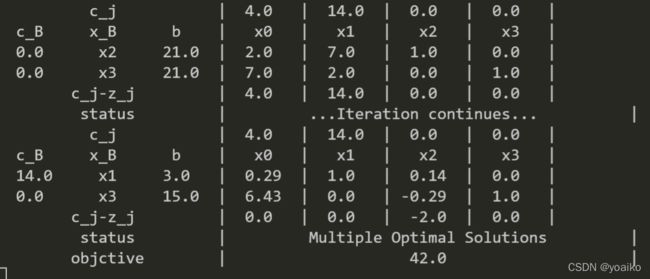
case 2 : Multiple Optimal Solutions
A = np.matrix([[2, 7, 1, 0],
[7, 2, 0, 1]], dtype=np.float64)
b = np.matrix([[21], [21]], dtype=np.float64)
c = np.matrix([4, 14,0,0], dtype=np.float64)
baseInd = [2, 3]
case 3 : Unboundedness
A = np.matrix([[1, -1, 1, 0],
[2, -1, 0, 1]], dtype=np.float64)
b = np.matrix([[10], [40]], dtype=np.float64)
c = np.matrix([2, 1,0,0], dtype=np.float64)
baseInd = [2, 3]