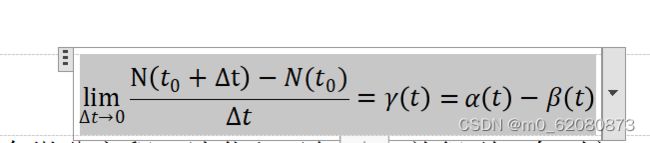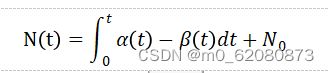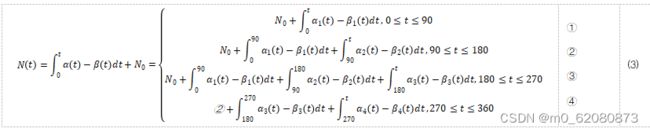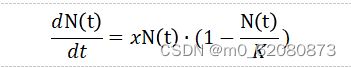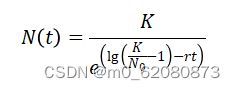探究蜜蜂种群变化影响因素
内容
1 问题的重述 1
1.1 问题的背景 1
1.2 问题的重述 1
2 假设和符号 2
2.1 假设 2
2.2 符号 2
3 模型分析与求解 3
3.1 蜜蜂种群的变化 3
3.2 灵敏度分析 4
3.3 问题预测 5
1 问题的重述
1.1 问题的背景
中国蜜蜂起源于古代喜马拉雅山的热带和亚热带雨林。它不仅适应了热带和亚热带雨林的生态条件，而且适应了我国的各种生态地理条件。广泛分布于长江流域亚热带常绿阔叶林和稻茶区。
但是，在全球蜜蜂数量下降的时候，不仅仅是在中国，这对一系列对人类福祉和生计至关重要的作物构成严重威胁，各国应该采取更多措施保护我们的主要盟友，抗击饥饿和营养不良。
在世界许多地方，蜜蜂和其他授粉媒介正在大幅减少，这主要是由于集约化耕作、单一栽培、过度使用农用化学品以及气候变化引起的气温上升，这不仅影响作物产量，还影响营养水平。如果这种趋势继续下去，水果、坚果和许多蔬菜等营养作物将越来越多地被水稻、玉米和土豆等主食作物所取代，最终导致饮食不均衡。“蜜蜂受到气候变化、集约化农业、农药使用、生物多样性丧失和污染等因素的巨大威胁。
通过查看数据并利用我们学到的知识，我们建立了模型来估计蜜蜂种群的变化以及影响它们的因素，以确定保护蜜蜂种群的方法。
1.2 问题的重述
蜜蜂授粉可以有效减少农业生产中化学激素和农药的使用，对保护动植物群落、维护自然生物多样性具有积极意义。目前，我国许多发达国家和部分省份已开始大规模推广提高蜜蜂授粉质量和产量的技术，取得了显著的生态效益和经济效益。
但自从2007年提出菌落崩溃障碍（CCD）的概念以来，它引起了很多关注。 随着研究的进行，很明显蜜蜂突然消失的原因并不单一，而是“相互作用”因素的组合。大量使用杀虫剂和杀虫剂对蜜蜂的健康构成严重威胁。各种因素，包括病毒的猖獗传播，捕食者和栖息地丧失，正在导致蜜蜂种群的减少。
我们需要建立模型来估计蜜蜂种群变化，找出影响蜜蜂种群变化的因素，并希望用模型来解决实际问题。
2 假设和符号
2.1 假设
假设1. 实验数据采集于安徽省南部地区。
假设2. 实验过程中没有天敌。
A假设 3. 在实验过程中没有蜜蜂进出，即迁入率、迁出率均为0。
假设4. 在实验过程中，蜜蜂有足够的食物和水。
假设5. 适宜的自然环境。
A假设 6. 一个月按 30 天计算。
A假设 7. 在理想条件下，蜜蜂孵化率为1，即一个可生殖蜜蜂必定产出一个幼卵。
我们基于上述假设建立了一个人口模型。当实验蜜蜂种群未达到环境容量或在一定时间内达到环境容量时，采用单一种群增长模型，即马尔萨斯模型和逻辑模型。
2.2 符号
在这项工作中，我们在模型构建中使用了表 1 中的命名法。其他不常用的符号一旦使用，就会被引入。
| 象征 | 定义 | 类型 |
|---|---|---|
| N0 | 蜜蜂初始数量 | 标量 |
| K | 环境容载量 | 标量 |
| r | 增长率 | 标量 |
| α | 自然出生率 | 标量 |
| β | 自然死亡率 | 标量 |
| N(t) | 蜜蜂种群随时间变化 | 函数 |
3 模型分析与求解
3.1 蜜蜂种群的变化
在第一个模型中，在蜜蜂生活在理想环境中，实验时间为一年的前提下，建立常微分方程来解决问题。根据该假设，蜜蜂种群仅受出生率和死亡率的影响，因此可以通过建立基于不同时间段蜜蜂出生率和死亡率的微分方程来构建马尔萨斯模型。
要求解这个微分方程，请代入已知的，并得到一年时间 N 和时间 t 中蜜蜂数量之间的关系：
在最佳条件下，出生率和死亡率是全年的出生率和死亡率。对于只有一年的实验期，预测模型过于笼统。因此，我们更仔细地选择时间段，以季度出生率和死亡率作为第一季度的单位，得到年度人口变化公式如下：
此外，我们认为，如果蜜蜂种群在一定时间内达到环境容量K，我们不仅要考虑出生死亡率，还要考虑内在增长率r。根据数据，我们得到了皖南蜜蜂种群的年龄比例（附图），设置r=kx，k是环境影响因子，x是成年蜜蜂在种群中的比例。因为只有成年蜜蜂才能出去采集花粉造蜜，而食物是否充足是种群产生大量后代并保证后代不死亡的关键，而且只有蜂王才能生育，所以成年蜜蜂的比例对出生率没有直接影响。我们根据逻辑模型构建常微分方程来求解：
我们可以用这个公式来解决它：
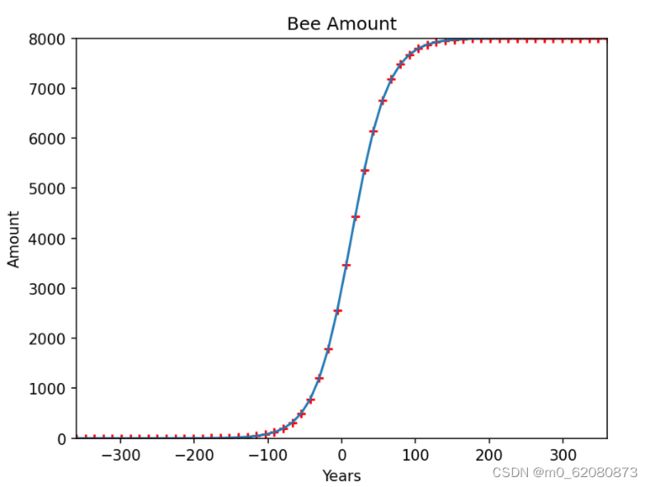
使用此公式制作变化曲线：
根据马尔萨斯模型，蜜蜂种群在达到环境容量K后不会无限制地继续增加，因此更符合自然条件下蜜蜂种群的增长。当初始值大于K时，则 N始终是t 大于零和某个T之间的递减函数，直到N（t）在N附近稳定，在一定的波动范围内。
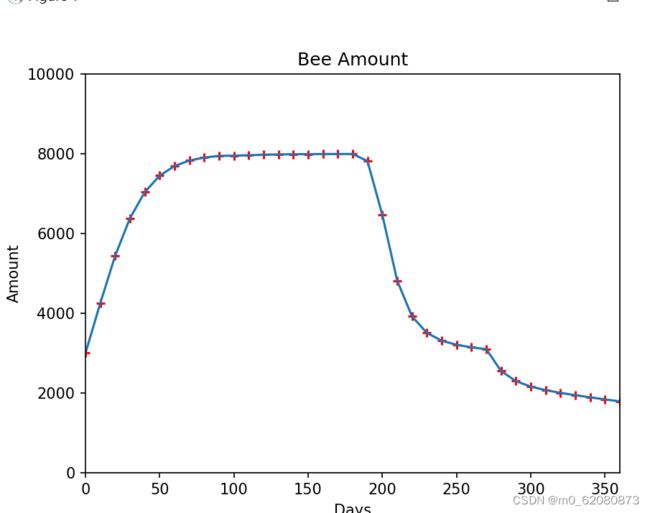
考虑到不同的环境影响因子和每个季度成年蜜蜂的比例，按季度分配了k和x的特殊值（每个季度的因子和年龄比），之后按照递归函数，以每十天为一个单位，每季度计算r的值，得出最终结果
r的计算：当前季度幼卵成活率*可生殖蜜蜂比例（假设所有可生殖蜜蜂均产卵）
得出如下结果（其中按照春夏秋冬四个季节平均分配360天）
与原始图相比，该图更接近实际种群变化，但由于时间跨度不够准确，无法进一步还原真实蜜蜂种群种群变化曲线。
附件：python环境下绘制图像代码：
import matplotlib.pyplot as plt
import math
e=2.71818
fig = plt.figure()
ax = fig.add_subplot(111)
ax.set(xlim=[0,360],ylim=[0,10000],title="Bee Amount",ylabel='Amount',xlabel='Days')
x0 = 3000
K = 8000
def X(t):
if t==0:
return x0
elif 03.2 灵敏度分析
对于本问题，由于问题中提供的信息不足以进行敏感性分析，我们参考了相关数据，决定从环境因素和年龄组成结构方面进行敏感性分析，使用公式（5）。通过计算N对K和r的偏导数，可以发现N对K 和 r都敏感，对K的敏感度大于对r的 敏感度。我们还使用python绘制了K和r分别变化20%时的人口曲线变化，进一步验证了结论。综上所述，年龄组和环境耐受性对N的影响较大的 是环境耐受性的变化。
3.3 问题预测
第三问：
首先，由于没有告知81000平方米花地的基本分布，所以必须要考虑土地形状对于蜂箱分布的影响，因此，我们只需要计算出相对最集中（圆形）和最分散（特殊的长方形）来计算最大值和最小值，并据此分析。
根据资料，一般来说，每平方米的土地上种植20只花，则81,000平方米的土地中最多可以种植81,000*20=1,620,000朵花。根据假设，由每只蜜蜂最多只能够传授2,000朵花，蜜蜂一般在距离蜂巢6,000m的距离采蜜，则定义一个蜂巢的影响花数量为R=20*6,000*6,000*π，向上取整，得到R=2,261,520,000朵。因此在这片区域中至少需要有2,261,520,000/2,000=1,130,760只蜜蜂。假设一个蜂箱有20000只蜜蜂活跃（即可以外出采蜜）则每一个蜂巢的影响区域内，最少需要的蜂箱的数量为1,130,760/20000=57个(向上取整)。
利用这个原理对各个假设进行模型求解。首先假设该区域的花卉分布十分特殊，即花卉全部均分布在蜜蜂的有效授粉范围，则利用最小圆覆盖定理可以很快就得：
这样子的圆面闭包一共有1个，则最少需要57个蜂箱；之后，根据所需面积和蜂箱影响面积的比值估算，按照蜂箱均匀散布，我们只需要1个蜂箱即可解决问题。
其次，根据资料，一朵花需要0.05平方米的土地，则假设一朵花所占据的最小土地是边长为
0.1
m（向上取整为0.3m），并假设花朵是排列在在一条宽度为0.3m的长方形上（以确保所需要的蜂箱数量最多），则在内部一个蜂巢x的影响范围是[x-6,000,x+6,000]，由已知条件可知这片土地的长为270,000m，则花朵的数量最多为270,000/0.3+1=900,001朵，因此每一个蜂巢的影响区间上的花的数量最多为12,000/0.3+1=40,001朵，则最多需要900001/40,001=23（向上取整）个区间才能够完全覆盖这片土地；此外，每个区间上需要40,001/2,000*20,000=1个蜂箱（向上取整），就可以实现花朵被完全授粉，因此至多需要1*23=23个蜂箱即可解决问题。
综合以上，我们最多需要准备23个蜂箱（平均每只蜂箱约20000只蜜蜂）即可完全覆盖所有情况。