感知器算法(Perceptron)
目录
引言
感知器
Matlab代码
效果展示
Python代码
效果展示
C++代码
效果展示
引言
本专栏第二个机器学习算法:感知器算法,全部代码通过Github下载,使用Matlab,Python以及C++三种语言进行实现。其中Matlab的代码可以直接运行,Python与C++的代码需要分别安装Numpy以及Numcpp两个库才能运行。
感知器
感知器算法主要用于二分类问题也可以应用于多分类(多分类算法后续会更新,本文只针对二分类),目标是通过训练绘制一条决策边界(分类线),这个分类线一般是随机初始化的,可以时随便的一条横线或者是一条竖线等等,通过不断地运行梯度下降使得分类线能够将训练数据划分开来。这里顺便提一嘴逻辑回归算法,其与感知器算法有点类似只是判断类别的方式存在差异。感知器算法致力于使得训练出权重w使得对于类别1:w*x>0,对于类别二:w*x<0。逻辑回归算法致力于训练出w和b两个参数使得 对于类别1:g( f(x) ) >0.5( f(x)=w*x+b , sigmoid用g(x)表示),对于类别二 g( f(x) ) < 0.5.
感知器算法判断方式如下:
在每次判断时,根据样本属于类别和w*x的值来判断。
1)如果训练样本x∈class1,而w*x>0,则权值w不变; 否则运行w‘=w+ρx,即对权值w进行修正。(ρ为学习率)
2)如果训练样本x∈class2,而w∗x<0, 则权值w不变; 否则执行w’=w−ρx,即对权值w进行修正。
以下程序都将完成的任务如下:
训练集坐标:
Class_1= [220 90;240 95;220 95;180 95;140 90];
Class_2= [80 85;85 80;85 85;82 80;78 80];
测试集坐标:
Test_Data = [180 90;210 90;140 90;90 80;78 80];
通过对训练集的训练,绘制一条决策边界(分类线)能够得到测试集的类别。
Matlab代码
clc;
close all;
clear all;
%% 定义训练样本
Class_1_o= [220 90;240 95;220 95;180 95;140 90];
Class_2_o= [80 85;85 80;85 85;82 80;78 80];
Test_Data_o = [180 90;210 90;140 90;90 80;78 80];
Class_x = mapminmax([Class_1_o(:,1)',Class_2_o(:,1)',Test_Data_o(:,1)'], 0, 1);
Class_y = mapminmax([Class_1_o(:,2)',Class_2_o(:,2)',Test_Data_o(:,2)'], 0, 1);
Class_1 = [Class_x(1:5)',Class_y(1:5)'];
Class_2 = [Class_x(6:10)',Class_y(6:10)'];
Test_Data = [Class_x(11:15)',Class_y(11:15)'];
[m_1,n_1] = size(Class_1);
[m_2,n_2] = size(Class_2);
%% 绘图程序
figure;
plot(Class_1(:,1),Class_1(:,2),'r*','LineWidth',2); hold on;
plot(Class_2(:,1),Class_2(:,2),'bo','LineWidth',2); hold on;
plot(Test_Data(:,1),Test_Data(:,2),'gs','LineWidth',2); hold on;
%% 增广向量
att_1=ones(m_1,1);
att_2=ones(m_2,1);
Train_Data = [Class_1,att_1; -1*Class_2,-1*att_2];
Test_Data = [Test_Data,ones(5,1)];
[m_3,n_3] = size(Train_Data);
w = randn([3 1]); % 随机初始化权重以及参数
a = 0.1; % 学习率
epoch = 0; % 定义迭代次数
%% 开始训练
while 1==1
% 找到分类错误的样本
b=w;
for i=1:m_3
if w'*Train_Data(i,:)' <= 0
w = w + a * Train_Data(i,:)';
end
end
if b==w
break;
end
epoch = epoch + 1;
end
%% 绘制最终分类线
f = [num2str(w(1,1)) '*x1+(' num2str(w(2,1)) ')*x2+(' num2str(w(3,1)) ')'] ;
h = ezplot(f,[0,1]);
grid on;
set(h,'Color','r');
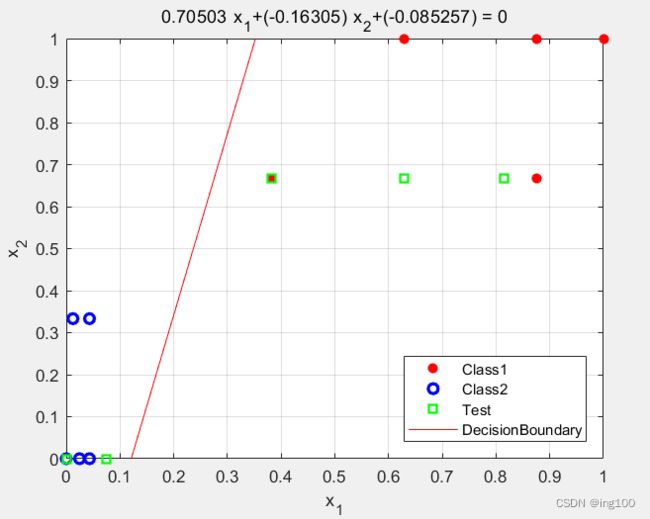
legend('Class1','Class2','Test','DecisionBoundary')
set(legend,'location','SouthEast')
%% 打印结果
for k=1:5
Result = w'*Test_Data(k,:)';
if Result > 0
fprintf('测试样本%d结果为%f属于第一类 \n',k,Result);
elseif Result <= 0
fprintf('测试样本%d结果为%f属于第二类 \n',k,Result);
end
end效果展示
这里权重w时随机初始化的,所以每次运行结果都不一样,但是都能正确被划分,这样可以避免梯度下降时出现局部最优解
Python代码
python需要用到numpy库,之前使用的pytorch,因为这个并不是所有人都安装了的所以改用numcpy了,代码如下
import matplotlib.pyplot as plt
# import torch
import numpy as np
# 进行归一化
def normalization(Data1, Data2, Data3):
# 要对全部的X坐标单独归一化,全部的Y坐标同理
Data_x = np.concatenate((Data1[:, 0], Data2[:, 0], Data3[:, 0]))
Data_y = np.concatenate((Data1[:, 1], Data2[:, 1], Data3[:, 1]))
# 参照Matlab的mapminmax函数进行归一化
Data_x = (Data_x - np.min(Data_x)) / (np.max(Data_x) - np.min(Data_x))
Data_y = (Data_y - np.min(Data_y)) / (np.max(Data_y) - np.min(Data_y))
Data_x = np.expand_dims(Data_x, 1)
Data_y = np.expand_dims(Data_y, 1)
Data1 = np.concatenate((Data_x[:5], Data_y[:5]), 1)
Data2 = np.concatenate((Data_x[5:10], Data_y[5:10]), 1)
Data3 = np.concatenate((Data_x[10:], Data_y[10:]), 1)
return Data1, Data2, Data3
if __name__ == "__main__":
# 定义数据集
class_1_o = np.array([[220, 90], [240, 95], [220, 95], [180, 95], [140, 90]], dtype=np.float)
class_2_o = np.array([[80, 85], [85, 80], [85, 85], [82, 80], [78, 80]], dtype=np.float)
Test_Data_o = np.array([[180, 90], [210, 90], [140, 90], [90, 80], [78, 80]], dtype=np.float)
Class_1, Class_2, Test_Data = normalization(class_1_o, class_2_o, Test_Data_o)
a = Class_1.shape
b = Class_2.shape
# 开始绘图
plt.figure()
plt.plot(Class_1[:, 0], Class_1[:, 1], 'r*', label='Class_1')
plt.plot(Class_2[:, 0], Class_2[:, 1], 'b*', label='Class_2')
plt.plot(Test_Data[:, 0], Test_Data[:, 1], 'gs', label='Test_Data')
plt.legend(loc='best')
# 增广向量
att_1 = np.ones((a[0], 1))
att_2 = np.ones((b[0], 1))
# 这里对数据集做了预处理使得 当正确分类是w * x > 0 ,错误分类是 w * x <= =
Train_Data = np.concatenate((np.concatenate((Class_1, att_1), axis=1), -1 * np.concatenate((Class_2, att_2), axis=1) ), axis=0)
Test_Data = np.concatenate((Test_Data, np.ones((5, 1))), axis=1)
c = Train_Data.shape
# w = np.random.randn(3, 1)
w = np.array([[1], [1], [1]]) # 使用[1;1;1]方便与C++的运行结果比对(因为C++无法使用matlpotlib绘图)
a = 0.1
# 开始训练
while True:
bb = w
for i in range(0, c[0]):
if np.matmul(w.T, Train_Data[i, :].T) <= 0: # matmul为矩阵乘法(线代知识)
w = w + a * Train_Data[i, :].reshape(3, 1)
if (bb == w).all():
break
print(w)
# 绘制分类线
xlist = np.linspace(-0.5, 1.5, 100)
ylist = np.linspace(-0.5, 1.5, 100)
x, y = np.meshgrid(xlist, ylist) # 计算圆所在区域的网格
f = w[0] * x + w[1] * y + w[2] < 0
plt.contourf(x, y, f, cmap="cool")
plt.show()
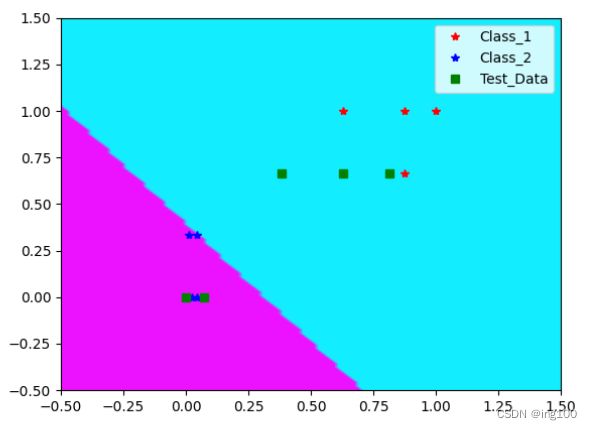
效果展示
下图是当权重w初始化为【1;1;1】时的训练结果,方便与C++的训练效果对比
C++代码
C++使用到了Numcpp库,没安装的朋友运行不了哦!
#include"NumCpp.hpp"
#include"boost/filesystem.hpp" // 这一行貌似可以去掉
#include
using namespace std;
tuple, nc::NdArray, nc::NdArray> normalization(nc::NdArray Data1, nc::NdArray Data2, nc::NdArray Data3);
void main()
{
// 定义数据集
nc::NdArray class_1_o = { {220,90},{240,95},{220,95},{180,95},{140,90} };
nc::NdArray class_2_o = { {80,85},{85,80},{85,85},{82,80},{78,80} };
nc::NdArray Test_Data_o = { {180,90},{210,90},{140,90},{90,80},{78,80} };
// 进行归一化Data是一个元组
auto Data = normalization(class_1_o, class_2_o, Test_Data_o);
auto Class_1 = get<0>(Data);
auto Class_2 = get<1>(Data);
auto Test_Data = get<2>(Data);
// 增广向量
auto att_1 = nc::ones({5,1});
auto Train_Data = nc::vstack({ nc::hstack({ Class_1, att_1 }), -1.0f * nc::hstack({Class_2,att_1}) });
Test_Data = nc::hstack({ Test_Data,att_1 });
// 定义训练的参数
//auto w = nc::random::randN({ 3,1 });
nc::NdArray w = {1,1,1};
w = w.reshape(3, 1);
float a = 0.1;
// 开始训练
while (true)
{
auto bb = w;
for (int i = 0; i < 10; i++)
{
// 这里与python不同numcpp进行向量相乘后得出的是一个1*1的矩阵,必须先用at()将数据提取出来后再进行if判断
if (nc::matmul(w.transpose(), Train_Data(i, Train_Data.cSlice()).transpose()).at(0) <= 0)
{
w = w + a * Train_Data(i, Train_Data.cSlice()).reshape(3, 1);
}
}
// 同理运行 bb == w 后得到的是一个1*1的矩阵,要用at()将数据提取出来
if ((bb == w).at(0))
{
break;
}
}
cout << w << endl; // 输出训练结果
}
// 归一化函数
tuple, nc::NdArray, nc::NdArray> normalization(nc::NdArray Data1, nc::NdArray Data2, nc::NdArray Data3)
{
// AXis::Row相当于python的axis=0 Data1(Data1.rSlice(),0)相当于python的 Data1[:,0]
auto Data_x = nc::concatenate({ Data1(Data1.rSlice(),0),Data2(Data2.rSlice(),0),Data3(Data3.rSlice(),0) }, nc::Axis::ROW);
auto Data_y = nc::concatenate({ Data1(Data1.rSlice(),1),Data2(Data2.rSlice(),1),Data3(Data3.rSlice(),1) }, nc::Axis::ROW);
// nc::min(Data_x) 返回1*1的矩阵需要用at(0)将数字提取出来再运算
Data_x = (Data_x - nc::min(Data_x).at(0)) / (nc::max(Data_x).at(0) - nc::min(Data_x).at(0));
Data_y = (Data_y - nc::min(Data_y).at(0)) / (nc::max(Data_y).at(0) - nc::min(Data_y).at(0));
Data1 = nc::concatenate({ Data_x({0,5},0), Data_y({0,5},0) },nc::Axis::COL);
Data2 = nc::concatenate({ Data_x({5,10},0), Data_y({5,10},0) }, nc::Axis::COL);
Data3 = nc::concatenate({ Data_x({10,15},0), Data_y({10,15},0) }, nc::Axis::COL);
tuple, nc::NdArray, nc::NdArray> Data(Data1,Data2,Data3); // 定义一个元组作为返回值
return Data;
} 效果展示
貌似也存在Matplotlib的C++版本,但是我没有安装。。。所以就直接打印训练结果了,可以看到训练结果与Python的一致,代表分类正确。