基于PCA和K-近邻算法的手写数字识别

PCA（Principal Component Analysis，主成分分析）是一种常用的数据分析方法。PCA通过线性变换将原始数据变换为一组各维度线性无关的表示，可用于提取数据的主要特征分量，常用于高维数据的降维。

网络上拥有很多PCA的解析，所以这里不赘叙PCA的数学算法原理，直接以手写数字识别的例子讲解PCA算法的应用。

scikit-learn是一个开源的Python机器学习工具包，拥有PCA算法、LDA算法和KNN等一系列基本算法的底层代码，运用其我们可以很轻易地实现我们想要执行的算法。scikit-learn自带了一些数据集，其中之一就是手写数字识别图片的数据集，该数据集拥有1797个训练样本，原始数据是8*8的图片。

from sklearn.datasets import load_digits
#导入自带的手写数字识别的数据
digits = load_digits()
X = digits.data
y = digits.target

# 把数据所代表的图片显示出来
images_and_labels = list(zip(digits.images, digits.target))
plt.figure(figsize=(8, 8), dpi=200)        #设置figsize为8*8，分辨率dpi为200
for index, (image, label) in enumerate(images_and_labels[:10]):
    plt.subplot(2, 5, index + 1)
    plt.imshow(image, cmap=plt.cm.gray_r, interpolation='nearest')
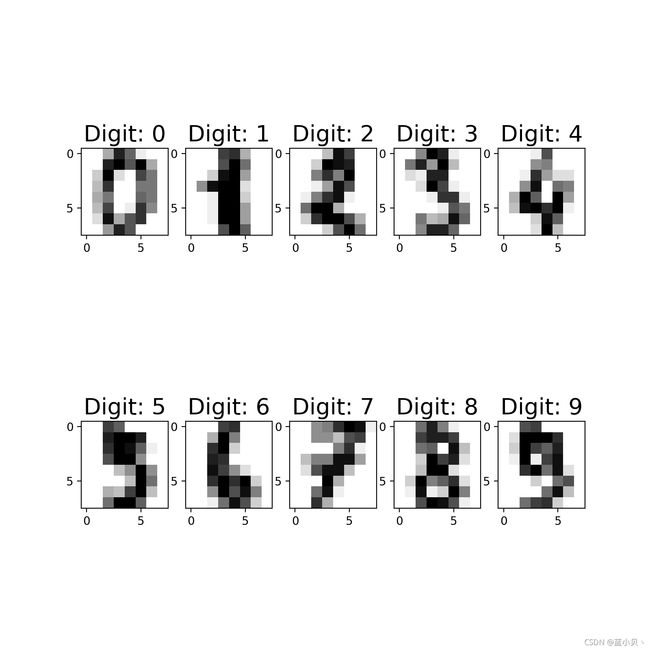
    plt.title('Digit: %i' % label, fontsize=20)
plt.show()   #操作环境在pycharm，所以放在循环外，绘制在同一张图片上

 上面对数据集内的数字种类做了一个展示，一共拥有0-9十类。接下来对数据集进行PCA降维，由于我们并不清楚降维到哪一个主成分才可以满足我们的数据量需求，所以接下来我们逐个测试得到我们所需要的降维成分。

max_pca =30  #最高降维
pcs = []
totexp_var = []
#逐个测试并绘制图像
for i in range(max_pca):
    pca = PCA(n_components=i+1)    #PCA降维
    reduced_X = pca.fit_transform(X_stand)       #降维
    tot_var = pca.explained_variance_ratio_.sum()  #数据含量总分
    pcs.append(i+1)
    totexp_var.append(np.round(tot_var, 3))

plt.plot(pcs, totexp_var, 'r')   #红色曲线
plt.plot(pcs, totexp_var, 'bs')  #蓝色方形描述
plt.xlabel('No. of PCs', fontsize=13)
plt.ylabel('Total variance explained', fontsize=13)

plt.xticks(pcs, fontsize=8)
plt.yticks(fontsize=10)
plt.show()

运行该代码后，我们会得到对应的数据降维到对应主成分个数时的数据还原率图像。

 在0-30的范围内数据的还原率还是不算优良的。像博主利用PCA降维高光谱图像，从200个波段到16个波段已经可以保留98%的数据还原率。接下来我将以20个主成分的降维后的手写数字识别数据集来使用K—近邻算法。

这里我将测试三种k=5的均值算法。分别为普通的k-近邻算法，带权重的k-近邻算法和指定半径的k-近邻算法。

x_train, x_test, y_train, y_test = train_test_split(X, y,
                                train_size=0.7, random_state=120)
#数据的标准化处理
sc = StandardScaler()
X_stand = sc.fit_transform(x_train)
y_stand = sc.transform(x_test)
#取贡献率大于80的成分数
pca_num = 20
#运用PCA降维
pca = PCA(n_components=pca_num)
newX = pca.fit_transform(X_stand)
#返回模型的各个特征向量
pca_comp = pca.components_
#切换至主成分
x_train_pca = pca.transform(x_train)
x_test_pca = pca.transform(x_test)

#测试三种不同的KNN均值算法的性能，其k值均设置为了5
models = []
#普通k-近邻算法
models.append(('KNN', KNeighborsClassifier(n_neighbors=5)))
#带权重的k-近邻算法
models.append(('KNN with weights', KNeighborsClassifier(n_neighbors=5, weights="distance")))
#指定半径的k-近邻算法
models.append(("Radius Neighboors", RadiusNeighborsClassifier(n_neighbors=5, radius=500.0)))

#分别训练三种模型，然后计算分数
#这里采用了交叉验证的方法
results = []
for name, model in models:
    kfold = KFold(n_splits=10)
    cv_result = cross_val_score(model, X, y, cv=kfold)
    results.append((name, cv_result))
for i in range((len(results))):
    print("name: {}; cross_val_score: {}".format(results[i][0], results[i][1].mean()))

 这里得到的结果表明，普通的k-近邻算法和带权重的均值算法的分数是一样的，所以为了简便起见，我接下来会使用普通的k-近邻算法去实现。

knn = KNeighborsClassifier(n_neighbors=5)
knn.fit(x_train_pca, y_train)         #pca降维后的数据输入
train_score = knn.score(x_train_pca, y_train)
test_score = knn.score(x_test_pca, y_test)
#输出准确性情况
print("train score: {}; test score: {}".format(train_score, test_score))

然后训练得到的模型份数为：

train score: 0.9840891010342084; test score: 0.9740740740740741

但后续我也通过模型预测真实图像的方式，得到了16张预测图，但其中预测错误了两张。

于是我再做了一组，预测错误了一张。总体而言，预测结果还算一般。结果图如下：

 

 以上为全部内容，由于作者为初学者，水平有限。所以以上仅为参考，如有错误，敬请指正！我会虚心向学，我们共同进步。