计算机视觉（四） 相机模型与参数标定
文章目录
-
- 一、概念及原理
-
- 1.1 相机标定的作用与意义
- 1.2 相机模型
- 1.3 相机标定的原理
- 1.4 相机标定的参数求解
- 二、 代码及运行
-
- 2.1 代码实现
- 2.2 运行结果
一、概念及原理
1.1 相机标定的作用与意义
畸变（distortion）是对直线投影（rectilinear projection）的一种偏移。简单来说直线投影是场景内的一条直线投影到图片上也保持为一条直线。畸变简单来说就是一条直线投影到图片上不能保持为一条直线了，这是一种光学畸变（optical aberration）,可能由于摄像机镜头的原因。
相机标定的作用在于消除由于相机产生的图像畸变,从而校正图像，为处理计算出精确数值提供可能。
由此，相机标定成了系统准确的先决条件。
从真实的三维世界坐标，可以得到二维的相机坐标，
但是我们从二维的相机坐标，能否准确的推算出真实的三维世界的坐标呢?这就是相机标定的意义。
1.2 相机模型
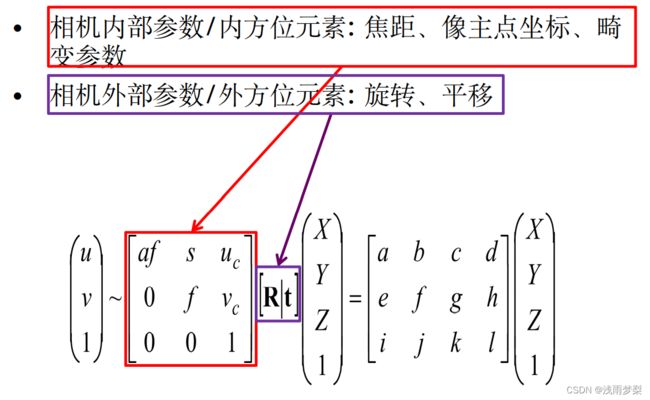
数码相机图像拍摄的过程实际上是一个光学成像的过程。相机的成像过程涉及到四个坐标系：世界坐标系、相机坐标系、图像坐标系、像素坐标系以及这四个坐标系的转换。
1.3 相机标定的原理
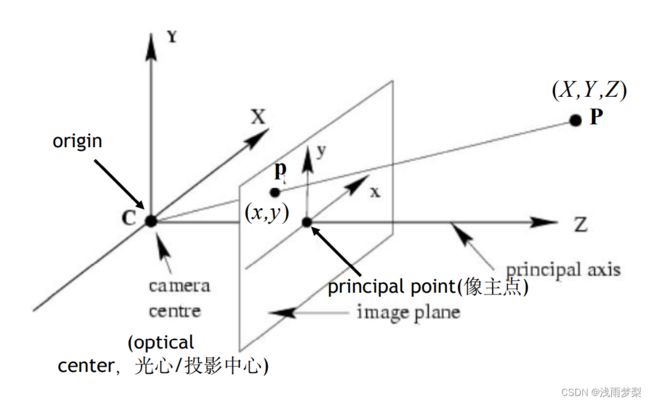
针孔相机成像原理其实就是利用投影将真实的三维世界坐标转换到二维的相机坐标上去，其模型示意图如下图所示：
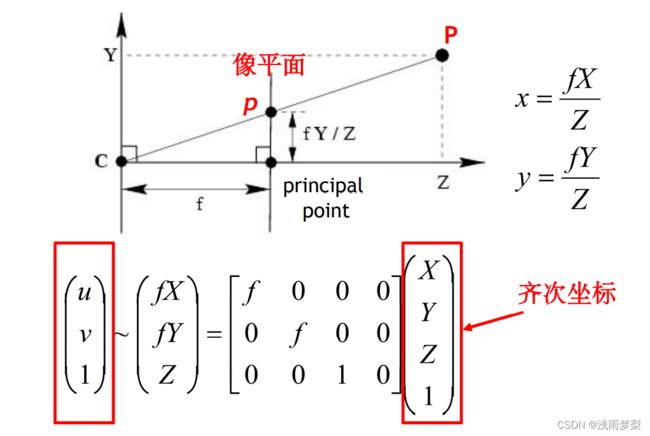
将三维坐标投影在二维坐标上，可以用如下方法表示：
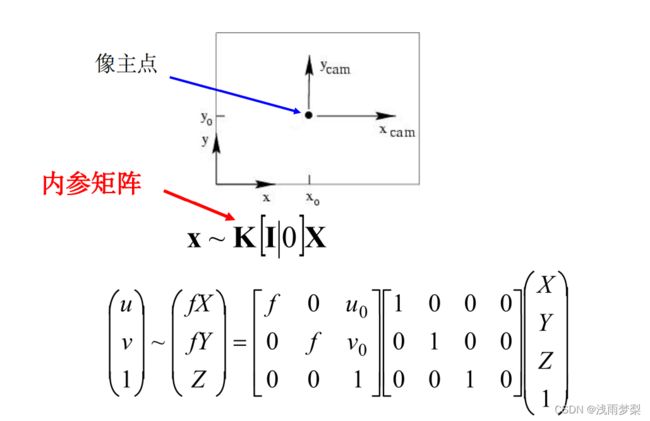
实际中，镜头并非理想的透视成像，带有不同程度的畸变。理论上镜头的畸变包括径向畸变和切向畸变，切向畸变影响较小，通常只考虑径向畸变。
径向畸变：
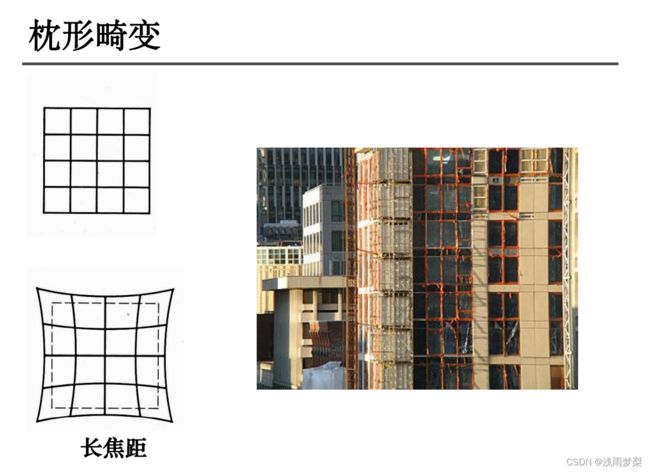
径向畸变主要由镜头径向曲率产生（光线在远离透镜中心的地方比靠近中心的地方更加弯曲）。导致真实成像点向内或向外偏离理想成像点。其中畸变像点相对于理想像点沿径向向外偏移，远离中心的，称为枕形畸变；径向畸点相对于理想点沿径向向中心靠拢，称为桶状畸变。
而畸变是如下原因导致：
– 透镜质量原因
– 光线在远离透镜中心的地方比靠近中心的地方更加弯曲
最终要求的未知数如下：
1.4 相机标定的参数求解
采用上图方法的困难是：
因此采用棋盘格标定法。
给出相关的参数定义：
算法流程如下：
- 打印一张棋盘方格图并贴在一个平面上
- 从不同角度拍摄若干张模板图像
- 检测出图像中的特征点
- 由检测到的特征点计算出每幅图像中的平面投影矩阵H
- 确定出摄像机的参数
关键在于求解平面投影矩阵H：
二、 代码及运行
2.1 代码实现
所用图像：
代码如下
# -*- codeing =utf-8 -*-
import cv2
import numpy as np
import glob
# 找棋盘格角点
# 阈值
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001)
#棋盘格模板规格
w = 11 #内角点个数，内角点是和其他格子连着的点
h = 8
# 世界坐标系中的棋盘格点,例如(0,0,0), (1,0,0), (2,0,0) ....,(8,5,0)，去掉Z坐标，记为二维矩阵
objp = np.zeros((w*h,3), np.float32)
objp[:,:2] = np.mgrid[0:w,0:h].T.reshape(-1,2)
# 储存棋盘格角点的世界坐标和图像坐标对
objpoints = [] # 在世界坐标系中的三维点
imgpoints = [] # 在图像平面的二维点
images = glob.glob('E:/CV/img/c4/*.jpg') # 标定所用图像
for fname in images:
img = cv2.imread(fname)
img = cv2.resize(img, (700, 375), interpolation=cv2.INTER_AREA)
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
# 找到棋盘格角点
# 棋盘图像(8位灰度或彩色图像) 棋盘尺寸 存放角点的位置
ret, corners = cv2.findChessboardCorners(gray, (w,h),None)
# 如果找到足够点对，将其存储起来
if ret == True:
# 角点精确检测
# 输入图像 角点初始坐标 搜索窗口为2*winsize+1 死区 求角点的迭代终止条件
cv2.cornerSubPix(gray,corners,(11,11),(-1,-1),criteria)
objpoints.append(objp)
imgpoints.append(corners)
# 将角点在图像上显示
cv2.drawChessboardCorners(img, (w,h), corners, ret)
cv2.imshow('findCorners',img)
cv2.waitKey(1000)
cv2.destroyAllWindows()
#标定、去畸变
# 输入：世界坐标系里的位置 像素坐标 图像的像素尺寸大小 3*3矩阵，相机内参数矩阵 畸变矩阵
# 输出：标定结果 相机的内参数矩阵 畸变系数 旋转矩阵 平移向量
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpoints, imgpoints, gray.shape[::-1], None, None)
# mtx：内参数矩阵
# dist：畸变系数
# rvecs：旋转向量 （外参数）
# tvecs ：平移向量 （外参数）
print (("ret:"),ret)
print (("mtx:\n"),mtx) # 内参数矩阵
print (("dist:\n"),dist) # 畸变系数 distortion cofficients = (k_1,k_2,p_1,p_2,k_3)
print (("rvecs:\n"),rvecs) # 旋转向量 # 外参数
print (("tvecs:\n"),tvecs) # 平移向量 # 外参数
# 去畸变
img2 = cv2.imread('E:/CV/img/c4/2.jpg')
h,w = img2.shape[:2]
# 我们已经得到了相机内参和畸变系数，在将图像去畸变之前，
# 我们还可以使用cv.getOptimalNewCameraMatrix()优化内参数和畸变系数，
# 通过设定自由自由比例因子alpha。当alpha设为0的时候，
# 将会返回一个剪裁过的将去畸变后不想要的像素去掉的内参数和畸变系数；
# 当alpha设为1的时候，将会返回一个包含额外黑色像素点的内参数和畸变系数，并返回一个ROI用于将其剪裁掉
newcameramtx, roi=cv2.getOptimalNewCameraMatrix(mtx,dist,(w,h),0,(w,h)) # 自由比例参数
dst = cv2.undistort(img2, mtx, dist, None, newcameramtx)
# 根据前面ROI区域裁剪图片
x,y,w,h = roi
dst = dst[y:y+h, x:x+w]
cv2.imwrite('E:/CV/img/c4/calibresult.jpg',dst)
# 反投影误差
# 通过反投影误差，我们可以来评估结果的好坏。越接近0，说明结果越理想。
# 通过之前计算的内参数矩阵、畸变系数、旋转矩阵和平移向量，使用cv2.projectPoints()计算三维点到二维图像的投影，
# 然后计算反投影得到的点与图像上检测到的点的误差，最后计算一个对于所有标定图像的平均误差，这个值就是反投影误差。
total_error = 0
for i in range(len(objpoints)):
imgpoints2, _ = cv2.projectPoints(objpoints[i], rvecs[i], tvecs[i], mtx, dist)
error = cv2.norm(imgpoints[i],imgpoints2, cv2.NORM_L2)/len(imgpoints2)
total_error += error
print (("total error: "), total_error/len(objpoints))
2.2 运行结果
所检测出的角点：
最终得到如下参数：
ret: 3.21963123287652
mtx:
[[1.62537252e+03 0.00000000e+00 3.00179929e+02]
[0.00000000e+00 1.66774993e+03 2.21777566e+02]
[0.00000000e+00 0.00000000e+00 1.00000000e+00]]
dist:
[[ 6.00174318e+00 -2.25158810e+02 9.00859551e-02 -2.50134530e-02
1.91729029e+03]]
rvecs:
(array([[-1.05297242],
[-0.57857674],
[-0.96488444]]), array([[-0.9893587 ],
[-0.72838336],
[-1.19529469]]), array([[-0.97946889],
[-0.85629254],
[-1.35461376]]), array([[-1.15682993],
[-0.24301077],
[-0.34117994]]), array([[-1.12338903],
[-0.2379929 ],
[-0.36847983]]), array([[-0.78359914],
[-0.35718904],
[-0.95027926]]), array([[-1.26734465],
[-0.01504808],
[-0.0772827 ]]), array([[-0.93056088],
[-0.83041804],
[-1.30635746]]), array([[-0.84323666],
[-0.15888891],
[-0.24198944]]), array([[-0.70859314],
[ 0.64729658],
[ 1.30887488]]), array([[-0.97264439],
[ 0.92906487],
[ 1.34793705]]))
tvecs:
(array([[-3.50678119],
[-0.6531044 ],
[54.30102517]]), array([[-3.62110881],
[ 0.83269952],
[43.0008585 ]]), array([[-0.86425096],
[ 3.24213622],
[58.52798279]]), array([[-5.00360174],
[-2.88587829],
[42.61840165]]), array([[-5.48465823],
[-3.50387247],
[44.97020503]]), array([[-8.72546186],
[ 0.53349194],
[60.69240914]]), array([[-4.50282276],
[-3.69978073],
[55.52448144]]), array([[-4.13553966],
[ 0.45807678],
[41.31170548]]), array([[-6.74641392],
[-3.06814878],
[61.02638646]]), array([[-1.20644347],
[-4.16893205],
[69.1035391 ]]), array([[ 4.45010736],
[-3.83553271],
[60.40680059]]))
total error: 0.32205649287848687
矫正出一个很奇怪的东西
原因可能是相机本来就没拍出畸变的图像。