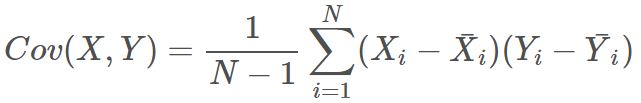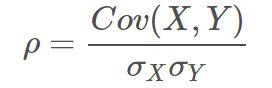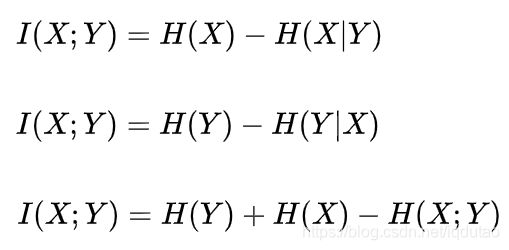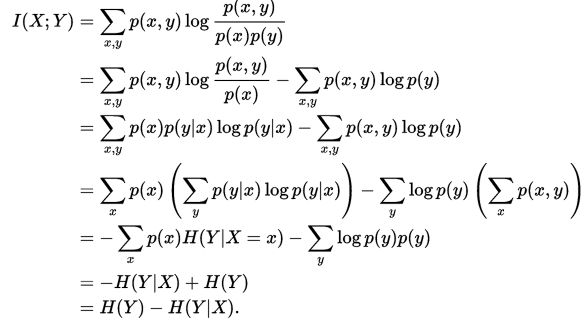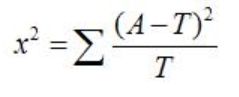机器学习-特征中的相关性及相关系数、卡方检验、互信息
在机器学习中,对于特征选择的方法分为三类:过滤式(Filter),包裹式(Wrapper),和嵌入式(Embedding)。过滤式方法是先按照某种规则对数据集进行特征选择,然后再训练学习器,特征选择过程与后续学习器无关,这相当于先用特征选择过程对初始特征进行“过滤”,再用过滤后的特征来训练模型。相关系数法、卡方检验法和互信息法是进行特征选择时常用的几种过滤式方法。
变量关系
协方差
线性相关系数
互信息
卡方检验和卡方分布
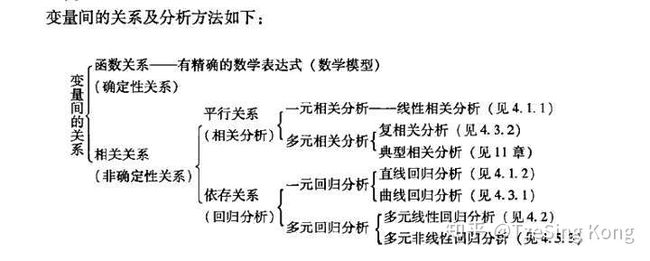
变量关系
先从变量之间的关系来说明,变量之间的关系可分为两类:
(1)存在完全确定的关系——称为函数关系,即类似于Y=2X+3;
(2)不存在完全确定的关系——虽然变量间有着十分密切的关系,但是不能由一个或多各变量值精确地求出另一个变量的值,那么这种关系称为相关关系,存在相关关系的变量称为相关变量。相关变量的关系也可分为两种:
(1)两个及以上变量间相互影响——平行关系;
(2)一个变量变化受另一个变量的影响——依存关系;
它们对应的分析方法:
相关分析是研究呈平行关系的相关变量之间的关系
回归分析是研究呈依存关系的相关变量之间的关系
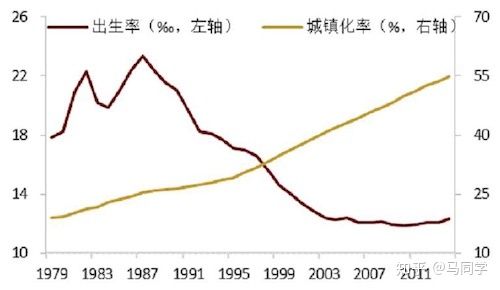
在这里我们主要研究变量与变量之间的相关分析,如下图,比如要买房的人越多,房价就越高,两者的关系称为正相关;从出生率和城镇化率我们可以看出是负相关。
类似上图中的这种相关性可以通过协方差和相关系数来具体表示和计算。
协方差
在概率论中,两个随机变量 X 与 Y 之间相互关系,大致有下列3种情况:
![]()
当 X, Y 的联合分布像左图那样时,大致上有: X 越大 Y 也越大, X 越小 Y 也越小,这种情况,我们称为“正相关”。
当X, Y 的联合分布像中间图那样时,大致上有:X 越大Y 反而越小,X 越小 Y 反而越大,这种情况,我们称为“负相关”。
当X, Y 的联合分布像右图那样时,既不是X 越大Y 也越大,也不是 X 越大 Y 反而越小,这种情况我们称为“不相关”。
同样将这3种相关情况,用一个简单的数字表达出来呢?,令 EX、EY 分别是 X 和 Y 的期望值。什么是期望呢?在这里我们可以把它看成是平均值,即 EX 是变量 X 的平均值,EY 是变量 Y 的平均值
在图中的区域(1)中,有 X>EX ,Y-EY>0 ,所以(X-EX)(Y-EY)>0;
在图中的区域(2)中,有 X
在图中的区域(3)中,有 X
在图中的区域(4)中,有 X>EX ,Y-EY<0 ,所以(X-EX)(Y-EY)<0。
当X 与Y 正相关时,分布大部分在区域(1)和(3)中,小部分在区域(2)和(4)中,所以平均来说,有E(X-EX)(Y-EY)>0 。
当 X与 Y负相关时,分布大部分在区域(2)和(4)中,小部分在区域(1)和(3)中,所以平均来说,有(X-EX)(Y-EY)<0。
当 X与 Y不相关时,在区域(1)和(3)中的分布,与在区域(2)和(4)中的分布一样多,平均来说,有(X-EX)(Y-EY)=0。
所以,我们可以定义一个表示X, Y 相互关系的数字特征,也就是协方差,即:
值得一提的是,E 代表求期望值,也可以用平均值来计算协方差:
当 cov(X, Y)>0时,表明X与Y 正相关;
当 cov(X, Y)<0时,表明X与Y负相关;
当 cov(X, Y)=0时,表明X与Y不相关。
协方差表示的是两个变量的总体的误差,这与只表示一个变量误差的方差不同。 如果两个变量的变化趋势一致,也就是说如果其中一个大于自身的期望值,另外一个也大于自身的期望值,那么两个变量之间的协方差就是正值。 如果两个变量的变化趋势相反,即其中一个大于自身的期望值,另外一个却小于自身的期望值,那么两个变量之间的协方差就是负值。这就是协方差的意义。
线性相关系数
我们已经知道了什么是协方差以及协方差公式是怎么来的,如果知道两个变量 X 与 Y 的协方差与零的关系,我们就能推断出 X 与 Y 是正相关、负相关还是不相关。那么有一个问题:协方差数值大小是否代表了相关程度呢?也就是说如果协方差为 100 是否一定比协方差为 10 的正相关性强呢?
假如X1、Y1 和 X2、Y2 分别联合分布图,如下所示:
显然,从图中可以看出,X1、Y1 和 X2、Y2 都呈正相关,而且 X1 与 Y1 正相关的程度明显比 X2 与 Y2 更大一些。接下来,我们计算两幅图的协方差看看是不是这样。
Cov(X1,Y1) = 37.5526
Cov(X2,Y2) = 3730.26
从两个协方差的值中,我们可以看出X2 与 Y2 的协方差竟然比 X1 与 Y1 的协方差还大100 倍。看来并不是协方差越大,正相关程度越高。这到底是为什么呢?其实,出现这种情况的原因是两种情况数值变化的幅值不同(或者量纲不同)。计算协方差的时候我们并没有把不同变量幅值差异性考虑进来,在比较协方差的时候也就没有一个统一的量纲标准。所以,为了消除这一影响,为了准确得到变量之间的相似程度,我们需要把协方差除以各自变量的标准差。这样就得到了相关系数的表达式:
![]()
即为:
为什么除以各自变量的标准差就能消除幅值影响呢?这是因为标准差本身反映了变量的幅值变化程度,除以标准差正好能起到抵消的作用,让协方差标准化。这样,相关系数的范围就被归一化到 [-1,1] 之间了。下面,我们就来分别计算上面这个例子中 X1、Y1 和 X2、Y2 的相关系数。
ρ(X1,Y1) = 0.9939
ρ(X2,Y2) = 0.9180
而线性相关分析,就是用线性相关系数来衡量两变量的相关关系和密切程度,线性相关系数一般通过皮尔逊相关系数(Pearson correlation coefficient)来解释相关性的强弱,公式即为:
皮尔森相关系数(Pearson correlation coefficient)也称皮尔森积矩相关系数(Pearson product-moment correlation coefficient) ,是一种线性相关系数,皮尔森相关系数是用来反映两个变量线性相关程度的统计量。考察两个变量的相关关系,首先得看清楚两个变量都是什么类型的,统计分析中常见的变量类型有连续型数值变量,无序分类变量、有序分类变量:
连续型数值变量:如销售额、气温、工资收入、考试成绩;
无序分类变量:如性别男和女,血型种类;
有序分类变量:如学历水平小学、初中、高中、大学、研究生;
适用范围
当两个变量的标准差都不为零时,相关系数才有定义,皮尔逊相关系数适用于:
(1)两个变量之间是线性关系,都是连续数据。
(2)两个变量的总体是正态分布,或接近正态的单峰分布。
(3)两个变量的观测值是成对的,每对观测值之间相互独立。
相关系数用r表示,其中n为样本量,分别为两个变量的观测值和均值,r描述的是两个变量间线性相关强弱的程度,r的绝对值越大表明相关性越强,系数的正负号代表正相关还是负相关。如果是0,代表没有相关。数值越接近1,相关性越强。
![]()
公式如下:
![]()
如下面每幅图上方的相关系数Cor(X1, X2)是计算出来的皮尔逊r值,从图中可以看出不同程度的相关性。
![]()
上图中,前三个具有高相关系数,我们可以选择把X1或者X2扔掉,因为他们似乎传递了相似的信息。
然而在最后一种情况,我们应该把两个特征都保留。
基于相关性的特征选择方法的一个最大的缺点就是,它只检测出线性关系(可以用一条直线拟合的关系),下图形象的展示出了相关性的缺陷:
![]()
这里的相关系数只是用来衡量两个变量线性相关程度的指标。也就是说,你必须先确认这两个变量是线性相关的,然后这个相关系数才能告诉你他俩相关程度如何,反之不成立。比如你先算出相关系数=0.9,就下结论说两个变量线性相关是不对的,甚至说两个变量相关(有某种更复杂的关系)也是不对的,如下图所示:
![]()
如图(右上)所示,非线性相关也会导致线性相关系数很大,并且如果两个变量的相关系数很大(0.816),那能不能说两者相关呢? 答案还是不能,为什么? 因为如图(右下)所示,很可能是一个离群点(outlier)导致了相关系数变得很大。另外,如果算出来相关系数=0,下结论说两个变量不是线性相关是ok的,但说他们完全不相关就得小心了,很有可能不对,如下图所示:
![]()
上图的相关系数计算结果为0,但你能说冰激凌的销量和温度不相关吗? 所以, Pearson Correlation Coefficient = 0只能说不是线性相关,但说不定会有更复杂的相关关系(非线性相关)。如果两个变量本身就是线性的关系,那么皮尔逊相关系数没问题,绝对值大的就是相关性强,小的就是相关性弱。但在你不知道这两个变量是什么关系的情况下,即使算出皮尔逊相关系数,发现很大,也不能说明那两个变量线性相关,甚至不能说他们相关,你一定要画出图来看才行,这就是为什么我们说眼见为实和数据可视化的重要性。
互信息
对于非线性关系,互信息就显得比较重要了,在进行特征选择时,我们不该把焦点放在数据关系的类型(线性关系)上,而是要考虑在已经给定另一个特征的情况下一个特征可以提供多少信息量。互信息会通过计算两个特征所共有的信息,把上述推理工程形式化表达出来。与相关性不同,它依赖的不是数据序列,而是数据的分布。
互信息的一个较好的性质在于,跟相关性不同,它并不只关注线性关系。如下图所示:
![]()
![]()
互信息的概念来自于信息熵,相信大家在很多机器学习,数据挖掘的数据都有看到,互信息广泛使用在特征选择、机器学习数模型中。在概率论和信息论中,互信息是两个随机变量的互信息(Mutual Information,简称MI)或转移信息是变量间相互依赖性的量度。通俗的来讲:互信息是一个随机变量包含另外一个随机变量的信息量,或者说如果已知一个变量,另外一个变量减少的信息量。顾名思义,互信息就是两件事为彼此提供的信息。当我知道了事件 A 之后,事件 B 的确定性增加多少,也就是让事件 B 减少多少的信息量。当中我们说一件事的信息量(或熵)就是你想知道这件事的发生需要多少信息。那么为什么相关的两件事会导致信息量的变化呢?举一个非常直观的例子,我们在做一个游戏,抛两枚硬币,然后猜两枚硬币分别是字还是花。每个人都会默认两枚硬币抛出字或花的概率相同,是1/2。猜出最终结果,我们需要的信息量是:
也就是如果你先问我第一枚硬币是字吗,我回答是或不是,然后你再问我第二枚硬币是字吗,我再回答一次,你就知道了两枚硬币的结果,信息量为二比特。那假如现在我告诉你第二枚硬币是我特制的,两面都是字呢?明显抛一次硬币得到的结果的信息量发生了一些变化,之前你需要问我两个问题,而现在只需要问一个就可以了,因为你已经知道第二枚硬币的结果一定是字。
由此就可以看出,当一个事件为另一个事件减少越多不确定性,这两个事件的相关性就越强。如果是两个独立事件,它们之间的相关性就是 0(后面也可以用公式验证),完全不相关。 例如知道第三枚硬币抛出字的概率并不会对你猜结果的两枚硬币的信息量造成任何影响。
用概率去解释也是一样的,我们知道熵也可以代表事件的随机程度,事件发生概率越小,所携带的信息量就越大。而两个事件 A,B,有 p(A|B)≥p(A),当 A,B 独立时有 p(A|B)=p(A)。由此也可以看出两件事的相关性。
到了这儿,其实我们已经把互信息定义好了。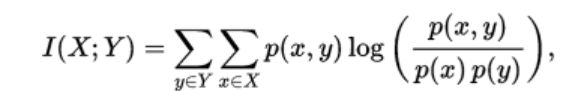
如果是连续随机变量就把求和替换为积分
另一种定义方法是:
其中上图中的 H(X),H(Y) 表示事件X,Y的信息,
H(X|Y)被称为条件熵:表示在知道事件X的情况下,此时再知道事件Y可以提供给我们的信息,
I(X;Y)被称为互信息:表示事件X和Y共同提供的信息;也可以理解为知道事件X可以对事件Y提供多少信息,反之亦然;
H(X;Y)被称为联合熵:表示事件X和Y之后可以提供给我们的信息,其中
注意到这组关系和并集、差集和交集的关系类似,用维恩图表示:
于是,在互信息定义的基础上使用琴生不等式,我们可以证明 I(X;Y) 是非负的,因此H(X)>=H(X|Y),这里我们给出 I(X;Y) = H(Y) - H(Y|X) 的详细推导:
在机器学习中,理想情况下,当互信息最大,可以认为从数据集中拟合出来的随机变量的概率分布与真实分布相同。
需要注意的是,互信息也是只能处理离散的特征。如果连续的情况,需要先离散化,计算每一对特征之间的归一互信息量。对于具有较高互信息量的特征对,我们会把其中一个特征扔掉。在进行回归的时候,我们可以把互信息量非常低的特征扔掉。对于较小的特征集合这种方式的效果或许还可以。但是,在某种程度上,这个过程会非常缓慢,计算量会以平方级别增长,因为我们要计算的是每对特征之间的互信息量。
卡方检验和卡方分布
卡方检验是一种用途很广的计数资料的假设检验方法。它属于非参数检验的范畴,主要是比较两个及两个以上样本率( 构成比)以及两个分类变量的关联性分析。其根本思想就是在于比较理论频数和实际频数的吻合程度或拟合优度问题。它在分类资料统计推断中的应用,包括:两个率或两个构成比比较的卡方检验;多个率或多个构成比比较的卡方检验以及分类资料的相关分析等。
以运营为例:
- 卡方检验可以检验男性或者女性对线上买生鲜食品有没有区别;
- 不同城市级别的消费者对买SUV车有没有什么区别;
如果有显著区别的话,我们会考虑把这些变量放到模型或者分析里去。
例1:四格卡方检验
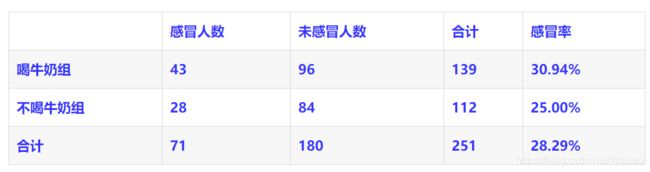
以下为一个典型的四格卡方检验,我们想知道喝牛奶对感冒发病率有没有影响,通过简单的统计我们得出喝牛奶组和不喝牛奶组的感冒率为30.94%和25.00%,两者的差别可能是抽样误差导致,也有可能是牛奶对感冒率真的有影响。
为了确定真实原因,我们先假设喝牛奶对感冒发病率是没有影响的,即喝牛奶和感冒时独立无关的,所以我们可以得出感冒的发病率实际是(43+28)/(43+28+96+84)= 28.29%
基于这个假设,假设的结果为:
计算出来后,假设的结果即下表:
原来实际的结果为:
如果喝牛奶和感冒真的是独立无关的,那么四格表里的理论值和实际值差别应该会很小。
差别的大小可以使用卡方检验来表示,卡方检验的计算公式为:
其中,A为实际值,T为理论值。X^2用于衡量实际值与理论值的差异程度(也就是卡方检验的核心思想),包含了以下两个信息:
(1)实际值与理论值偏差的绝对大小(由于平方的存在,差异是被放大的)
(2)差异程度与理论值的相对大小
X^2分布有两个主要用途为用于检验拟合优度,也就是可以检验一组数据与指定曲线的拟合程度,或检验某组观察值是否符合某种分布,检验两个变量的独立性,通过这个方法检查两个变量之间是否存在某种关联
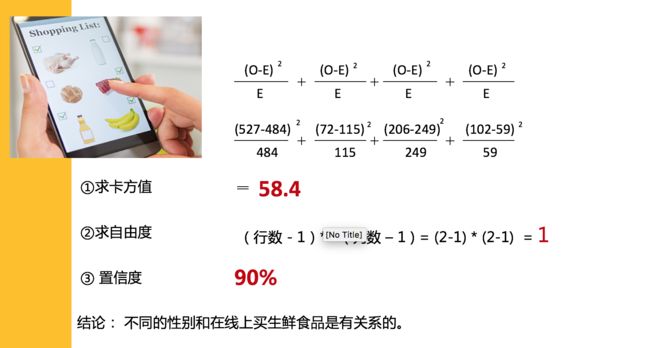
回到上面的例子,实际计算的结果为:
上一步我们得到了卡方的值,但是如何通过卡方的值来判断喝牛奶和感冒是否真的是独立无关的?也就是说,怎么知道无关性假设是否可靠?答案是,通过查询卡方分布的临界值表。我们需要查询卡纸分布的临界值,将计算的值与临界值比较。
![]()
查询临界值就需要知道自由度,如何计算自由度?只要一种可能的话,自由度是0,有两种可能,自由度是1。如果抛不是一个硬币,而是一颗台球,上面数字只有一种可能,此时自由度是0。一个药片,吃下去的有三种结果:病治愈,病恶化,病不变,如果吃下去只有治愈这个可能,自由度是0,如果有三种可能,自由度是2。对于本例的表格而言,行和列的自由度都有自己的自由度,分别是行数和列数减一。又考虑到行数和列数的乘积是表中数值的总数,因此全表对应的自由度是行和列自由度的乘积。本例的自由度由此计算出来是1。
注:卡方检验的自由度:
1)如果是独立性检验,那么自由度就等于(a-1)*(b-1),a b表示这两个检验条件的对应的分类数。
比如《问卷与量表数据分析》课程里面的性别和是否购买之间的独立性检验,自由度就等于(2-1)*(2-1)=1。这里可以理解为有两个约束条件,即性别和是否购买这两个变量,这两个变量约束的方向都是自己那一方面的,所以要在自己的类别数目后面减去1,而不是总的类别数减去总的约束条件数目。
2)适合性检验,类别数减去1。此处相当于约束条件只有一个
自由度V=(行数-1)*(列数-1);
对四格表,自由度V = 1,查询可得 临界值为3.84
对V = 1,喝牛奶和感冒95%概率不相关的卡方分布的临界概率是:3.84,显然1.077<3.84,没有达到卡方分布的临界值,所以喝牛奶和感冒是独立不相关的。
例2 投硬币
根据投硬币观察到的正面,反面次数,判断这个硬币是均衡的还是不均衡。
现在有一个正常的硬币,我给你投50次,最好的情况肯定是25个正面,25个反面,如果我不知道这个硬币是不是均衡的,我想用正面,反面的频次来判断,我投了50次,其中28个正面,22个反面。我怎么用卡方检验来证明这个硬币是均衡的还是不均衡的呢?
![]()
我们拿到这3个信息,去查表,因为0.72小于查表得到的3.841,所以我们得出这个硬币是均衡的结论。
![]()
例3 投筛子
有一个筛子,我不知道它是不是均衡的,于是我打算投36次看一下。
按照投硬币的方式,我先要画出一个表格,然后计算出3个数值,
带着这3个值,我们去查表,于是我们得出这个现象不能判定他是个均衡的筛子。
例4 业务场景
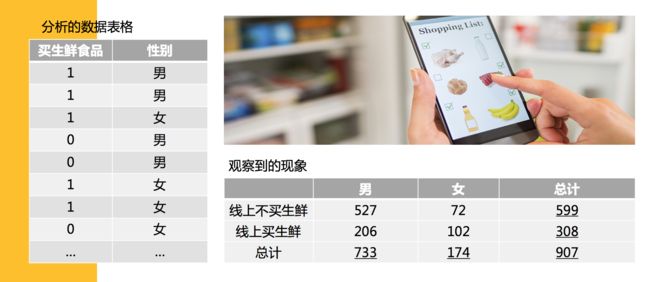
电商中消费者的性别和购买生鲜,我们要观察性别和在线上买不买生鲜食品有没有关系,现实生活中,女性通常去菜市场买菜的比较多,那么在线上是不是也这样。
我们得出观察到数据,并且形成表格后,我们需要计算理论的数据,在上面的例子我们发现,我们发现有66%的人不在线上买生鲜(599除以907),34%的人会在线上买。 那如果,男的有733个人,女的有174个人,根据这些比例,我们可以得出的理论值是什么呢?
根据理论和实际值,我们可以算出卡方值,自由度,并且结合我们定义的置信度,查表得到性别和线上买生鲜是显著相关的。
所以我们如果下次看到一个女性来访问我们的网站,多投放一些广告,说不定会转化哦。
本文主要介绍了线性相关系数、卡方检验、互信息三个概念。
1. 线性相关系数,基于两个变量在线性的基础上,主要用来衡量两个变量的线性相关的程度,其它类型的相关性pearson相 关 系 数就无法衡量了。
2. 卡方检验基于两个样本会遵守特定的理论分配,用来检验两个样本or变量是否独立。计算也相对比较简单。能做大小比较,但是如果判断自变量与因变量是否相关,需要查卡方临界表。
3. 互信息基于信息熵理论,可以作为变量间相互依赖性的量度,涉及log计算,计算稍微复杂些。后面两个方法都只能计算离散特征,如果是连续特征,需要先将特征离散化之后再进行计算。
4. 特征选择时:卡方检验,偏向于选择出现次数较少的特征。因为是期望-观测值的平方再除以期望,互信息不会出现这个情况。因为互信息有乘以p(x,y)p(x,y)。从大多数实验来看,卡方跟互信息效果差不多,看具体的数据集而定。
参考链接:https://zhuanlan.zhihu.com/p/94074441
参考链接:https://www.jianshu.com/p/26004ad8872e
参考链接:https://www.zhihu.com/question/304499706/answer/544609335
参考链接:https://my.oschina.net/peterlie/blog/546761/print
参考链接:https://zhuanlan.zhihu.com/p/36441826
参考链接:https://blog.csdn.net/LiuXF93/article/details/88956643
参考链接:https://www.matongxue.com/madocs/568.html
参考链接:https://www.zhihu.com/question/20852004
参考链接:https://blog.csdn.net/shingle_/article/details/51725054
参考链接:https://www.jianshu.com/p/807b2c2bfd9b