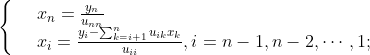数值分析·学习 | 解线性方程组的直接方法（高斯消去法以及LU求解）matlab实现
目录
一、前言：
二、算法描述：
三、实现代码：
1、高斯消去法：
2、高斯消去法-列主元消去法：
3、LU分解：
4、求逆矩阵：
四、总结：
一、前言：
个人学习内容分享
二、算法描述：
1、高斯消去法：
设有线性方程组
或写为矩阵形式
如果
，则可通过高斯消去法将Ax=b约化为等价的三角形线性方程组，形式如下：
计算公式如下：
消元计算(k=1,2,···,n-1)
回代计算
2、高斯消去法-列主元消去法：
1.det←1
2.对于k=1,2,···,n-1
（1）按列选主元
（2）如果
,则停止计算(det(A)=0)
（3）如果
则转（4）
换行：
（4）消元计算
对于i=k+1,···,n
对于j=k+1,···,n
（5）
3.如果
，则计算停止（det(A)=0）
4.回代求解
（1）
（2）对于i=n-1,···,2,1
5.
3、LU分解：
计算U的第r行，L的第r列元素（r=2,3,...,n）:
求解Ly=b,Ux=y的计算公式：
三、实现代码：
1、高斯消去法：
function x=Gauss_Elimination_Method(A)
%功能：一般的高斯消元法
%依次消元
for k=1:length(A)-2
for m=1:length(A)-1-k
A(k+m,:)=A(k+m,:)-A(k+m,k)/A(k,k).*A(k,:);
end
end
%回代求解X
x=zeros(length(A)-1,1);
for k=1:length(A)-1
temp=length(A)-k;
x(temp,1)=(A(temp,length(A))-sum(A(temp,1:length(A)-1)*x(:,1)))/A(temp,temp);
end
end2、高斯消去法-列主元消去法：
function x=Gauss_Elimination_Method_GAI(A)
%功能：列主元的高斯消元法
%依次消元
for k=1:length(A)-2
temp1=max(A(k:length(A)-1,k));
for m=k:length(A)-1
if A(m,k)==temp1
temp1=A(m,:);
A(m,:)=A(k,:);
A(k,:)=temp1;
continue;
end
end
for m=1:length(A)-1-k
A(k+m,:)=A(k+m,:)-A(k+m,k)/A(k,k).*A(k,:);
end
end
%回代求解X
x=zeros(length(A)-1,1);
for k=1:length(A)-1
temp3=length(A)-k;
x(temp3,1)=(A(temp3,length(A))-sum(A(temp3,1:length(A)-1)*x(:,1)))/A(temp3,temp3);
end
end3、LU分解：
function x=LU(A,b)
%功能：LU算法
L=eye(length(A));
for k=1:length(A)-1
for m=1:length(A)-k
L(k+m,k)=A(k+m,k)/A(k,k);
A(k+m,:)=A(k+m,:)-A(k+m,k)/A(k,k).*A(k,:);
end
end
y=L\b;
x=A\y;
end4、求逆矩阵：
function X=Inverse_matrix(A)
%功能：求逆矩阵
L=length(A);
I=eye(L);
A=[A,I];
for k=1:L-1
for m=1:L-k
A(k+m,:)=A(k+m,:)-A(k+m,k)/A(k,k).*A(k,:);
end
end
for k=1:L-1
for m=L-k:-1:1
if A(m+1,:)==0
continue;
else
A(m,:)=A(m,:)-A(m,L+1-k)/A(L+1-k,L+1-k).*A(L+1-k,:);
end
end
end
for k=1:L
A(k,:)=A(k,:)/A(k,k);
end
X=A(:,L+1:2*L);
end四、总结：
高斯消去的原理：矩阵化三角形阵，
选主元的目的是为了降低大数除小数造成的误差放大。
LU分解的原理：将矩阵划分为一个上三角矩阵U和下三角矩阵L，需要注意的是下三角矩阵L的对角线元素为1。