报童模型（2）--经济学含义和应用

1. 报童模型

大家买菜的时候有没有注意到一个很有趣的现象。当市场开放时，季节性农产品、面包和坚果充斥着餐桌和食品摊。然而，当一天的销售结束时，放草莓的桌子几乎空了，而你仍然可以在另一张桌子上看到很多的可以供选择坚果商品。

为什么会这样？草莓销售商是否可能经常低估需求？为什么供应商没有适应这种模式并调整供应以更好地满足需求？　

我们可能不知道这些供应商的具体情况，但我们可以使用报童模型框架来更好地了解他们每周面临的权衡。

报童模型是运营管理中的一个标准问题，用于在不确定情况下做出最佳容量/库存决策。

下面为英文版的定义或者说对报童模型的解释：

An entrepreneurial newsvendor buys the daily newspaper from the distributor early
in the morning.

They try to sell as many papers as they can during the day.
At the end of their shift, they salvage what they couldn’t sell.

How many papers should the newsvendor buy?

一位企业家在清晨从报纸发行商那里购买日报。

他们试图在白天销售尽可能多的报纸。

在轮班结束时，他们打折销售处没有销售出去的报纸。

报童应该买多少份报纸？

2. 最优采购量

我们进一步细细分析一下报童模型以及报童的最优订购量到底应该是多少呢？

简言之，做出报纸的采购决策中需要在拥有过多的报纸（供大于求）和没有足够的报纸（供不应求）之间找到一个最好的平衡。

让我们介绍一些符号并将问题框架确定下来。  

Cu: 表示报纸短缺一个单位的成本（通常是单位利润）

Co：表示未售出库存单位的成本（通常以原始成本-残值或另一时期库存估计成本为特征）

f()：表示报纸的需求概率密度函数；

F()：表示报纸需求累积密度函数 

基于上面的符号定义，我们需要问：  每一天最佳的库存单位数量(也就是报童应该订购的最佳决策数量Q∗)。

根据经济学中的定义，当边际收益等于边际成本时，即达到最优，因此如果我们要找到最佳的报纸采购量Q∗，可以将每个单元的边际收益预期边际成本进行比较。假设我们计划有Q单位的报纸量，并且正在考虑再增加一个单位，那么此时的数量就等于Q+1。

因此，只要增加的下一个单元的边际收益大于边际成本，那么我们就可以继续计划额外库存。因为只要边际收益大于边际成本，我们买一份报纸总是有利可图，因此我们就可以继续多进一份报纸的库存，这样就不断的提高收益，当边际收益等于边际成本时，既可以得到最大的报纸订购量。

假设我们预期订购量Q的报纸总量，那么如果市场对报纸的需求量大于Q，这种情形发生的概率为1-F(Q)，假设我们在多订购一份报纸，因此销售这多一份的报纸获取的收益为Cu*(1-F(Q))。这个收益是因为市场需求大于Q，而我们仅仅订购量Q，这样我们就失去了这一份市场收益。

而如果我们确实订购了Q+1份的报纸，但是实际需求却为Q，那么这一份多订购的报纸就相当于说需要贱卖了，那么这一份多订购带来的损失就等于Co，而这种情形发生的概率是F(Q)，因此此种情形下，我们的损失为Co*F(Q)。

因此根据经济学的边际收益=边际成本，那么当Cu*(1-F(Q))=Co*F(Q)时，我们就得到了最优的采购量：

即

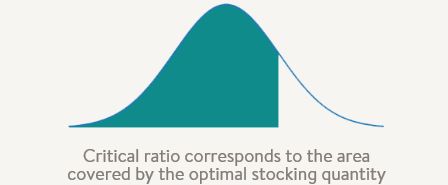
上述方程的右侧有时称为临界比。这个比率介于0和1之间，它对应于库存决策要涵盖的总不确定性的多少。

不易腐烂的产品将具有较高的临界比率，尤其是在利润率较高的情况下（例如，碳粉盒、罐头食品、坚果等）。另一个极端是高度易腐烂的产品，如航空座椅和时尚产品。在这种情况下，临界比率很可能低于0.5。我们可以把这些情况看作是决策者应该计划出售所有库存（飞机座位，当然还有草莓）的情况。

事实证明，仅就易腐性（超龄成本）而言，坚果销售商和草莓销售商的风险状况（需求不确定性、超龄成本和未足龄成本）是截然不同的。草莓销售商可能想在当天结束前用完存货：未售出的可能不值得再带回下一个市场，而坚果销售商可以在未来一天轻松出售未售出的存货。

对大多数公司来说，估算缺货存时的成本可能相对简单——错过盈利机会是一个好的初步估计。如果需要对客户保留的效果进行鉴定，则复杂性可能会增加（转向其他品牌的客户往往不会再回来，而缺货成本可能大于利润率）。当需要考虑替代产品的影响时，可能会产生额外的复杂性（供应商库存不足，但一些客户会转而购买可能有库存的同等产品，从而导致缺货成本低于利润率）。

估计过度订购的影响可能最终也会比较复杂。资本成本（不在别处使用资本的机会成本）和在另一个周期库存产品的成本是很好的起点，但这种方法可能会错过额外的超额成本。例如，产品退货和报废成本可能很难量化，尤其是当报废成本仅在产品清零时发生时。

估计决策期内的需求范围也是值得研究的。木子在这篇文章中，假设我们可以从历史数据中获得一系列需求场景，从而能够大致了解需求分布，但是实际生产和销售过程中，对于公司来说，根据一系列价值而不是点估计值进行操作是非常重要的，此外对于新产品的销售量和一些老产品的未来销售量，我们都可能无法完全获知，因此也就不知道其具体的概率分布形式，那么这就可能需要用到很多机器学习的方法对其进行产品销售、相类似产品的销售数据和历史的综合分析才能确定了，2022年，也有很多经济学和管理学顶刊在这一研究中得以遍地开花，即假设产品的需求分布是未知的，从实际数据中寻求分布的规律和答案，即我们常常听到的数据驱动的管理和预测。​

Never Late: 好饭不怕晚，爱一个人只要勇敢表达也不晚，想要跳出舒适圈也不晚，Wan蛋的是你永远不愿意迈出最初的第一步。

木子在CSDN技术社区开设了技术专栏，搜索“爱听雨声的北方汉”，关注木子技术博客，和木子一起学习Matlab/Mathematica/C++/Python/机器学习/数据分析等课程，让乏味的生活因学习而更快乐！

另外，如果想在线学习上述编程语言，也可以直接点击下面链接，进入学习：

C++：    https://edu.csdn.net/course/detail/37772

Python:   https://edu.csdn.net/course/detail/37774