杂质半导体中的载流子浓度
1.电子（空穴）占据施主能级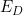
(受主能级
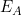)的概率有多大，杂质未电离的几率？
那么对于施主来说，施主未电离几率（电子占据施主能级的几率）
施主能级要么是有一个电子占据，自旋方向任意，要么就是离化了（和费米分布有点差别）
受主未电离的几率
，既然有没有电离的几率，施主离化（电离）的几率，
，这就是电离的可能性，同样受主电离的几率
，涵盖了所有情况
若施主杂质
，施主能级上的电子浓度
--------未电离的施主浓度
,这就是参杂了这么多电子，没有电离的施主，同样离化的施主浓度就出来了，离化的施主带正电
,这些是离化的施主
那么定量表达式就都有了
若受主浓度
，受主能级上的空穴浓度
--------未电离的受主浓度
,这是掺入的受主当中有这么多没有离化
离化的受主杂质
这就是两种杂质的荷电情况
对于杂质半导体我们以N型半导体为主线（N型的处理方式与P型是一样的）
讨论 杂质电离情况与
的值有关
若
,则
,其实我们还可以从能带图上看，杂质能级比费米能级高了这么多，代表有电子的概率非常小，所以几乎全部电离到导带上去了
若
,费米能级和施主能级重合，则
,这个条件非常重要，费米能级和施主能级重合，刚好有三分之一离化，另外三分之一没有离化
做这么几个式子，主要是准备工作
2.N型半导体的载流子浓度？
前边我们介绍了本征半导体的载流子浓度，我们怎么求的？
然后再乘以指数项（用本征半导体的电中性条件，然后再代入各自的表达式）
对于常用的半导体来说，费米能级在禁带中线
我们按照相似的思路处理
首先列出N型半导体的电中性条件(在一个N型半导体里面，单位体积正电荷和负电荷总量相等)
一个N型半导体，以电子导电为主，施主离化提供了一些导带电子，施主本来是中性的，离化之后。形成正电中心，对于一个N型半导体，价带电子获得能量跃迁到导带（这个叫本征激发），电子和空穴成对出现，对于一个N型的杂质半导体，导带电子的来源渠道有两个，（杂质离化和本征激发）施主里面，有离化的和非离化的，这样的话，我们可以写电中性条件，
,我们把它化简以下，
,在电中性条件的表达式里面，把各自的表达式代入进去
,大家注意在这个关系式里面，对于一个N型半导体，就费米能级我们还不清楚
我们想要求出费米能级的解析式，这个式子太过于复杂
这样的一个对N型半导体来说，普遍适用的关系，按照一定条件分段讨论，施主的荷电状态分两种，温度很低，施主一定不能好好电离，在升高就会电离的更多
我们应该根据样品温度区间的不同分段讨论，我们应该从低到高来
（1）低温区间，杂质离化的不多，低温弱电离区--------指的是温度极低，杂质离化很少，所对应的温度区间(温度的分界线很模糊，我们可以把每个区间说清楚)，条件可以等效成
,在低温弱电离区
，杂质离化的很少，可见本征激发的贡献更少，可以直接忽略，电中性条件退化为
，得到
,
,这就是在低温弱电离区，费米能级的表达式，![\small E_F=\frac{E_c+E_F}{2}+\frac{1}{2}k_0T[\ln{\frac{N_D}{2}}-\ln{\frac{2(2\pi m_n^* k_0)^{\frac{3}{2}}}{h^3}}-\frac{3}{2}\ln T]](http://img.e-com-net.com/image/info8/5c87755df7d54a829f050c850319585f.gif){kind=small}
,既然温度非常低，
的时候，费米能级
,
，在施主能级和导带顶的中心位置上，费米能级高于杂质能级，所以没有办法好好电离
我们从![\small \frac{dE_F}{dT}=\frac{1}{2}k_0\ln{\frac{N_D}{2N_c}}+\frac{1}{2}k_0T[-\frac{3}{2}\cdot \frac{1}{T}] =\frac{1}{2}k_0[\ln{\frac{N_D}{2N_c}}-\frac{3}{2}]](http://img.e-com-net.com/image/info8/8313ed50f54749d4800e0b682a4a8e18.gif){kind=small}
，令这个式子=0，我们求出极值点，
,
达到极大值，
,随T上升增大，极值点左边，当
,随T上升下降,都是半导体硅，都在低温弱电离区，但是施主浓度大小不一样，达到极大值的时候，温度是不一样的，表明越大，达到极大值需要的温度高，费米能级达到极大值所需要的温度越高
费米能级的极大值出现在低温弱电离的情况下（温度非常高，本征激发比施主能级高的多，这个时候变得电子空穴一样多，本征激发为主费米能级跑中间去了），费米能级不是在温度高的时候，就高，电子空穴一样多，费米能级只能在中线，将低温弱电离区得到的费米能级表达式
代入
中，
![\small =N_cexp(-\frac{\Delta E_D}{2k_0T})(\frac{N_D}{2N_c})^{\frac{1}{2}}=[\frac{N_DN_c}{2}]^{\frac{1}{2}}exp(-\frac{\Delta E_D}{2k_0T})](http://img.e-com-net.com/image/info8/b66e672fc80c4b7a88cfcc9fc544f1ea.gif)
,取对数
,用N型样品，然后做低温下的变温实验
也就是设定一个温度
，设定不同温度，测得不同的浓度，然后作图，斜率就是
（2）中间电离区，温度升高，杂质离化变多，所对应的温度区间 ， 在中间电离区，费米能级可以降至
以下区域，当，
离化，
未离化，显然是中间电离区，但是又没有强电离
（3）温度继续升高，杂质离化继续增加，90%以上离化，就变成了强电离区，杂质充分电离，杂质充分电离，温度老在这边升高，杂质充分离化，有两种情况（1.本征激发忽略不计 2.温度继续升高，本征激发不可忽略），我们说的强电离区说的是杂质充分电离，本征激发可以忽略不计所对应的温度区间---------半导体器件和集成电路正常工作的区间
电中性条件
，这就是强电离区的电中性条件
此时载流子浓度就出来了
费米能级和电子浓度有一一对应关系，
,这就是在强电离情况下费米能级的表达式，
eg: 室温下的硅，若施主浓度
，在这个情况下，往里面一代，
我们就可以得到
,费米能级在导带底之下0.0266ev的地方，这个距离是
表明相对导带底的距离，这样一看就知道是非简并半导体，N型半导体满足玻尔兹曼分布条件，大于