图形学中那些你需要知道的变换概念

前言

在前面的OpenGL ES 教程中，随着教程的进展，我们介绍并使用过很多变换矩阵，但没有系统总结过图形学涉及到的种种变换，因此这篇文章再次回顾“变换”这个主题。

变换

通俗来讲，所谓的变换就像编程中调用一个函数，向这个函数传入一个点的坐标$(x,y)$，函数会返回另一个点的坐标$(a,b)$。一个点到另一个点的映射就是变换。在图形学中我们通常使用矩阵来表示变换，矩阵复杂在它涉及的数学知识，但是对于编程实现来说它相当简洁。

因为矩阵乘法一般不满足交换律，我们需要约定乘法的顺序：设$v$是变换前的向量，$M$是变换矩阵，$v^{\prime }$是变换后的向量。习惯上我们把变换矩阵放在$v$的左边，也就是说矩阵$M$左乘向量$v$
$$v^{\prime }=M\cdot v$$
上面的式子就代表了一次变换。

如果对向量应用多个变换矩阵，根据应用这些变换的先后顺序，后变换的矩阵放在左边。例如以下矩阵代表向量$v$先应用矩阵$M_1$，再应用矩阵$M_2$：
$$v^{\prime }=M_2\cdot (M_1\cdot v)$$

二维变换

我们先来介绍一些基本变换在二维平面中的表达形式，二维中的变换可以推广到三维空间中。

在二维平面中，变换前、变换后的向量的分量用以下字母表示：
$$\begin{gathered} v=\left[\begin{array}{c}x\\ y\end{array}\right] \\ {v}^{\prime }=\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right] \end{gathered}$$

缩放

顾名思义，缩放就是一个缩小或者放大的过程，如下图：

如果我们假设缩放倍数为 s，那么缩放变换前后的坐标变化如下：
$$\begin{gathered} x^{\prime }=sx \\ {y}^{\prime }=sy \end{gathered}$$
接下来，我们从上式中总结出缩放矩阵。如果你不是很明白所谓的矩阵是如何总结出来的，不妨添加另一个系数为0的分量：
$$\begin{gathered} x^{\prime }=sx+0y \\ {y}^{\prime }=0x+sy \end{gathered}$$
上面两个式子的运算结果等价于以下的矩阵—向量运算，x 和 y 前的系数与矩阵中的元素一一对应：
$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}s& 0\\ 0& s\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]$$
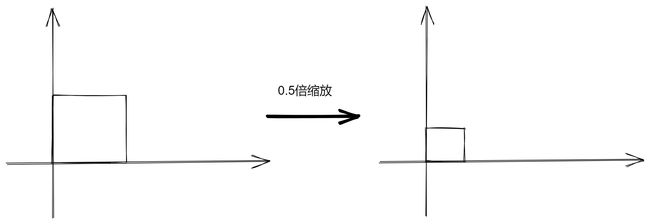
缩放变换并没有要求 x 和 y 的缩放倍数必须完全一致，下图就展示了 x 的缩放倍数是 0.5 而 y 的缩放倍数是 1.0 的情况：

因此，矩阵中 x 、y 的缩放倍数可以不是同一个数，我们得到二维的缩放变换矩阵：
$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}{s}_x& 0\\ 0& s_y\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]$$

错切

假设一个正方形的边长为 1 ，那么沿着 x 轴进行错切（Shear）变换之后，效果类似下图所示：

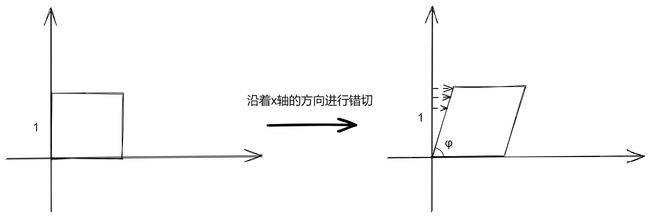
实质上，错切变换对所有点进行了平移，只不过平移的距离不是固定的，这个距离与到 x 轴的距离成正比，越靠近 x 轴，平移的距离越小，在 x 轴上的点平移距离为0。

在平面几何中，错切变换更严格的定义为沿固定方向移动每个点，移动量与平行于该方向并穿过原点的线的带符号距离成比例。

虽然错切变换与选择的方向有关，但是我们不打算深入定义错切变换，姑且认为它沿着 x 轴方向进行平移就好。根据上图，我们定义错切角为$\phi$，计算错切因子$a=\cot \phi$（换句话说， $a=$ 最大位移 / 最大y值），那么可以写出变换前后的如下等式：

$$\begin{gathered} x^{\prime }=x+ay \\ {y}^{\prime }=y \\ \Rightarrow \left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}1& a\\ 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right] \end{gathered}$$

上面的等式非常容易理解，因为 y 坐标表示了到 x 轴的距离。

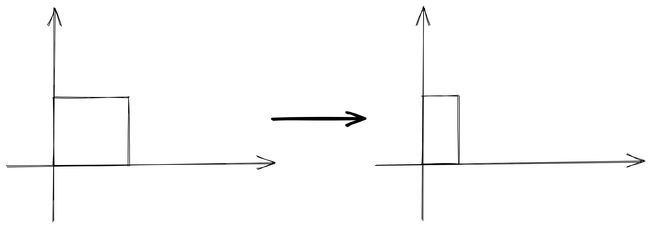
需要加以区分的一个要点是，错切变换并不等同于在现实生活中挤压纸箱子，有两个理由来说明这一点。第一个理由是错切变换至少要保证 x 或 y 其中一个维度的坐标不变，而挤压纸箱子的过程中，由于纸箱子的边长不会改变，因此在二维平面上看起来，x 和 y 同时发生了变化。如下图所示：

另一个理由则是，错切变换是等面积变换，变换前后几何体的面积并没有改变。而上图挤压的过程中，几何体的面积变小了。不需要严格的数学证明也能够说明这一点，想想生活中我们打算把纸箱子压扁以减少它们占用的空间，占用的空间即体积等于底面积乘以高，如果底面积在我们挤压的过程没有发生变化的话，它们占用的体积也应当不会变化才对！

旋转

在之前的教程中我们已经讨论过旋转矩阵，并对二维旋转矩阵给出过一个推导的方式。这里我们用另一种更简洁的方式再进行一遍推导。

一次旋转包括了三方面的内容：围绕着什么旋转、旋转的方向以及旋转的角度。习惯上我们一般规定坐标原点为旋转点，逆时针为正方向。我们规定围绕着坐标原点而旋转是为了计算和推导的方便，你可能会对此有所疑问，如何表示围绕着其他点的旋转呢？我们将在“变换分解”这一节详细解答。而规定逆时针为正方向仅仅是一个习惯，大多数图形学 API 都是这么规定的。

假设平面中有一个向量$c$，在旋转之前，它和 x 轴的夹角是$\alpha$，对它进行旋转变换，旋转$\beta$角度之后，得到的新的向量是$c^{\prime }$，如下图所示：

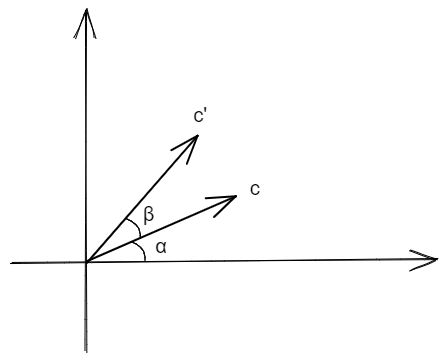
根据角度容易得知旋转前$c$的坐标和旋转后$c^{\prime }$的坐标：
$$\begin{gathered} c=(x,y)=(|c|\cos \alpha ,|c|\sin \alpha ) \\ {c}^{\prime }=(x^{\prime },y^{\prime })=(|c^{\prime }|\cos (\alpha +\beta ),|c^{\prime }|\sin (\alpha +\beta )) \end{gathered}$$
旋转前后向量的模长并没有发生变化，因此有$|c|=|c^{\prime }|$。运用三角公式可得：
$$\begin{gathered} x^{\prime }=|c^{\prime }|\cos (\alpha +\beta )=|c^{\prime }|(\cos \alpha \cos \beta -\sin \alpha \sin \beta ) \\ =|c|\cos \alpha \cos \beta -|c|\sin \alpha \sin \beta \\ =x\cos \beta -y\sin \beta \\ {y}^{\prime }=|c^{\prime }|\sin (\alpha +\beta )=|c^{\prime }|(\sin \alpha \cos \beta +\sin \beta \cos \alpha ) \\ =|c|\sin \alpha \cos \beta +|c|\cos \alpha \sin \beta \\ =x\sin \beta +y\cos \beta \end{gathered}$$
根据上述化简式，我们可以得到下述旋转矩阵，其中$\beta$指代旋转的角度：
$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}\cos \beta & -\sin \beta \\ \sin \beta & \cos \beta \end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]$$

平移与齐次坐标

平移应该是最容易理解的一个变换了，假设沿着 x 轴平移的距离为$t_x$，沿着 y 轴平移的距离为$t_y$，可以得到：
$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{c}x\\ y\end{array}\right]+\left[\begin{array}{c}{t}_x\\ t_y\end{array}\right]$$
平移变换到这里似乎就讨论完了。但是，回顾一下我们一开始提出的对变换的期待，我们希望能够使用矩阵左乘也就是$M\cdot v$的形式来表示每一个变换。对于前面介绍的缩放、错切、旋转矩阵，这个条件都满足了，可是我们没有总结出与平移变换有关的矩阵。事实上，二维空间的平移变换确实无法用2x2的矩阵来表示。为了能够用矩阵乘法表达平移变换，我们引入齐次坐标的概念。（我们在以前的教程中介绍过齐次坐标，但并没有说明为什么一定要引入这个概念。）

所谓齐次坐标，其实就是在正常的坐标分量中额外添加了一个新的分量$w$，比如说对于普通的二维坐标$(x,y)$，它的齐次坐标就是$(x,y,w)$。对于不同的对象，w 的值有所不同。把一个点的二维坐标扩展为齐次坐标时，我们令其w=1。那么，对于一个二维向量的扩展，显然它的 w 应该为0。因为在齐次坐标的角度来看，向量 = 点 - 点，自然而然 w=0。

• 扩展坐标时，二维点 = $(x,y,1)$
• 扩展坐标时，二维向量 = $(x,y,0)$

把一个点的齐次坐标还原成二维坐标的时候，只需要令 x 和 y 分量除以 w 分量即可：齐次坐标$(x,y,w)$对应着二维坐标$(x/w,y/w)$。根据这个定义，我们会发现 (2,3,1)、(4,6,2)、(6,9,3) 等齐次坐标表示的都是同一个点 (2, 3)。而在齐次坐标下，“点+点“也具有特殊的几何含义：点 + 点 = 两点形成的线段的中点。

既然二维点使用齐次坐标来进行表达，变换矩阵自然需要升维到3x3。2x2的矩阵无法用乘法来表达平移变换，但是3x3的矩阵可以：
[ x ′ y ′ 1 ] = [ 1 0 t x 0 1 t y 0 0 1 ] [ x y 1 ] = [ x + t x y + t y 1 ] \begin{bmatrix} x'\\y' \\1 \end{bmatrix}= \begin{bmatrix} 1 & 0 & t_x\\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x\\y \\1 \end{bmatrix}=\begin{bmatrix}x+t_x\\y+t_y\\1\end{bmatrix} ​x′y′1​ ​= ​100​010​tx​ty​1​ ​ ​xy1​ ​= ​x+tx​y+ty​1​ ​
因为我们引入了齐次坐标的概念，因此前面介绍的其他变换矩阵也需要进行升维，新的维度中只需要保持变换前后 w 不变，其余填充0即可。我们用 Scale 表示缩放矩阵，Shear 表示错切矩阵，Rotate 表示旋转矩阵：
S c a l e = [ s x 0 0 0 s y 0 0 0 1 ] S h e a r = [ 1 a 0 0 1 0 0 0 1 ] R o t a t e = [ cos ⁡ β − sin ⁡ β 0 sin ⁡ β cos ⁡ β 0 0 0 1 ] Scale=\begin{bmatrix}s_x&0&0\\0&s_y&0\\0&0&1\end{bmatrix}\\ Shear=\begin{bmatrix}1&a&0\\0&1&0\\0&0&1\end{bmatrix}\\ Rotate= \begin{bmatrix} \cos\beta & -\sin\beta & 0\\ \sin\beta & \cos\beta & 0\\ 0 & 0 & 1\end{bmatrix} Scale= ​sx​00​0sy​0​001​ ​Shear= ​100​a10​001​ ​Rotate= ​cosβsinβ0​−sinβcosβ0​001​ ​

逆变换

逆变换就是把变换后的物体还原到变换前的状态，既然我们使用矩阵来表示变换的概念，那么逆变换自然对应着逆矩阵。

比如，如果我们有一个平移变换矩阵$M$，它把点(3,3)平移到(4,5)：
M = [ 1 0 1 0 1 2 0 0 1 ] [ 4 5 1 ] = [ 1 0 1 0 1 2 0 0 1 ] [ 3 3 1 ] M=\begin{bmatrix}1 & 0 & 1\\ 0 & 1 & 2 \\ 0 & 0 & 1\end{bmatrix}\\ \begin{bmatrix}4\\5 \\1 \end{bmatrix}= \begin{bmatrix}1 & 0 & 1\\ 0 & 1 & 2 \\ 0 & 0 & 1\end{bmatrix} \begin{bmatrix}3\\3 \\1\end{bmatrix} M= ​100​010​121​ ​ ​451​ ​= ​100​010​121​ ​ ​331​ ​
那么，对应于矩阵$M$的逆矩阵$M^{-1}$就可以把点(4,5)平移回到(3,3)，它表示对上面平移变换的逆变换：
M − 1 = [ 1 0 − 1 0 1 − 2 0 0 1 ] [ 3 3 1 ] = [ 1 0 − 1 0 1 − 2 0 0 1 ] [ 4 5 1 ] M^{-1}=\begin{bmatrix}1 & 0 & -1\\ 0 & 1 & -2 \\ 0 & 0 & 1\end{bmatrix}\\ \begin{bmatrix}3\\3\\1 \end{bmatrix}= \begin{bmatrix}1 & 0 & -1\\ 0 & 1 & -2 \\ 0 & 0 & 1\end{bmatrix} \begin{bmatrix}4\\5\\1\end{bmatrix} M−1= ​100​010​−1−21​ ​ ​331​ ​= ​100​010​−1−21​ ​ ​451​ ​
求矩阵的逆其实是一个比较复杂的问题，我们不在这里过多展开。

变换组合与变换分解

我们依次介绍了常用的二维变换所对应的变换矩阵，一次矩阵相乘就代表执行一次变换。如果我们需要对点 a 执行一系列的变换$A_1、A_2、A_3、\cdots A_n$，会得到以下的乘法链：
$$A_n(...A_2(A_1(a)))$$
然而我们也知道，虽然矩阵乘法不满足交换律，但是它满足结合律，我们既可以从右到左，对点 a 应用一个又一个的矩阵，也可以先把所有单个的变换矩阵相乘，整合为矩阵$M$：
$$A_n(...A_2(A_1(a)))=(A_n\cdots A_2\cdot A_1)a=Ma$$
在具体的编程实现中，如果我们坚持一步步对点 a 应用变换矩阵$A_1\cdots A_n$，就要消耗很多额外空间来保存这n个变换矩阵的值，显然只保留最终的矩阵$M$更好。而且用一个变量我们就能求出$A_n\cdots A_2\cdot A_1$相乘的结果：先令$M=A_n$，计算$M\cdot A_{n-1}$的结果并且赋值给$M$，依此类推。

将一些单步的变换矩阵整合为一个复杂的变换矩阵的过程，我们称作变换的组合，把变换组合在一起能够帮助我们提高程序的性能。预先计算好变换矩阵不仅节省内存，也减小了对许多点组成的物体应用变换时的计算量。

在推导平移变换的时候，为什么我们坚持把平移变换整合成矩阵乘法的形式而不是继续使用加法呢？我们希望能够把所有变换以乘法的方式组合成一个矩阵，这就是一个很重要的原因。如果我们仍然以加法的方式处理平移，那么多个变换的表达式会变得相当臃肿，表达式的臃肿意味着编程实现上的低效。

把缩放、错切、旋转、平移变换矩阵都乘在一起的时候，它的形式看起来就像下面这样：
M = [ a b t x c d t y 0 0 1 ] M= \begin{bmatrix} a & b & t_x \\ c & d & t_y \\ 0 & 0 & 1 \end{bmatrix} M= ​ac0​bd0​tx​ty​1​ ​
其中，a、b、c、d 这四个系数都有可能被具体的缩放、错切、旋转矩阵所影响，这三个变换真正起作用的系数就保存在这四个位置中；$t_x$和$t_y$体现的是平移变换中的距离；矩阵的第三行是0，0，1，含义是保持 w 不变。

既然简单的变换可以组合成复杂的变换，那么反过来思考，我们想实现一个复杂的变换的时候，是不是可以考虑把它分解为简单的变换呢？这就是我们接下来想要讨论的一个概念：变换的分解。

我们再次列出尚未解决的这个问题：给定一个不是原点的二维点$B$，如何表达一个物体$N$围绕这个点进行旋转的变换？（这个问题在“旋转”一节中提到过）

“围绕着其他的点进行的旋转”可以被我们视作一个复杂的变换。面对这个问题，我们这样处理：

1. 让点$B$和物体$N$一起平移，点$B$平移到坐标轴原点$O$处。我们记平移变换矩阵为$T(B)$
2. 物体$N$围绕着原点$O$进行旋转。我们记旋转矩阵为$R(\beta )$
3. 最后，还是让点$B$和物体$N$一起平移，点$B$平移回到原来的位置。我们记平移变换矩阵为$T(-B)$

虽然，我们的确只知道围绕着原点做旋转的矩阵是什么样子的，但是，我们可以先把点$B$和物体一起平移到原点那里，然后就可以运用我们熟悉的旋转矩阵！只要记得旋转完后再把它们平移回去就行。把平移与旋转一组合起来，我们就可以表达出围绕着二维平面中任意一点$B$进行旋转的旋转矩阵$M$：
$$M=T(-B)\cdot R(\beta )\cdot T(B)$$

三维变换

当我们把视线投向三维变换矩阵时，很容易就能发现那些组成三维矩阵的系数基本上是对二维矩阵的扩展。另外，三维中齐次坐标的规则和二维一致，以下给出4x4的三维变换矩阵：
S c a l e = [ s x 0 0 0 0 s y 0 0 0 0 s z 0 0 0 0 1 ] T r a n s l a t i o n = [ 1 0 0 t x 0 1 0 t y 0 0 1 t z 0 0 0 1 ] Scale=\begin{bmatrix}s_x&0&0&0\\0&s_y&0&0\\0&0&s_z&0\\0&0&0&1\end{bmatrix}\\ Translation=\begin{bmatrix}1&0&0&t_x\\0&1&0&t_y\\0&0&1&t_z\\0&0&0&1\end{bmatrix}\\ Scale= ​sx​000​0sy​00​00sz​0​0001​ ​Translation= ​1000​0100​0010​tx​ty​tz​1​ ​
在三维空间中，旋转变得更加复杂了一些。围绕着 x、y、z 坐标轴逆时针旋转$\alpha$角度的旋转矩阵如下：
R x ( α ) = [ 1 0 0 0 0 cos ⁡ ( a ) − sin ⁡ ( a ) 0 0 sin ⁡ ( a ) cos ⁡ ( a ) 0 0 0 0 1 ] R y ( α ) = [ cos ⁡ ( a ) 0 sin ⁡ ( a ) 0 0 1 0 0 − sin ⁡ ( a ) 0 cos ⁡ ( a ) 0 0 0 0 1 ] R z ( α ) = [ cos ⁡ ( a ) − sin ⁡ ( a ) 0 0 sin ⁡ ( a ) cos ⁡ ( a ) 0 0 0 0 1 0 0 0 0 1 ] R_x(\alpha)=\begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & \cos(a) & -\sin(a) & 0 \\ 0 & \sin(a) & \cos(a) & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\\ R_y(\alpha)=\begin{bmatrix} \cos(a) & 0 & \sin(a) & 0\\ 0 & 1 & 0 & 0 \\ -\sin(a) & 0 & \cos(a) & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\\ R_z(\alpha)=\begin{bmatrix} \cos(a) & -\sin(a) & 0 & 0\\ \sin(a) & \cos(a) & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} Rx​(α)= ​1000​0cos(a)sin(a)0​0−sin(a)cos(a)0​0001​ ​Ry​(α)= ​cos(a)0−sin(a)0​0100​sin(a)0cos(a)0​0001​ ​Rz​(α)= ​cos(a)sin(a)00​−sin(a)cos(a)00​0010​0001​ ​
上面的矩阵看上去吓人，但其实并不难理解。想象一下，有一个物体绕着 x 轴旋转，它在转的过程中，所有点的 x 坐标肯定不会发生变化，因此$R_x(\alpha )$的第一行是1，0，0，0，而 y、z 坐标的变化等同于二维旋转，所以你会看到很熟悉的那些系数。不过，稍微有点奇怪的是，为什么绕着 y 轴旋转的矩阵不太一样？这和向量叉乘的顺序有关。根据右手定则，$x\times y=z$、$y\times z=x$，但是对于坐标轴 y，$z\times x=y$。这么说可能会有些抽象，我们给出 xoy平面和 zox 平面的俯视图：

zox 平面中的 “x” 相当于 xoy 平面中的 “y”，所以 zox 平面中的点在旋转前后有以下的表达式：
$$\begin{gathered} z^{\prime }=z\cos \alpha -x\sin \alpha \\ {x}^{\prime }=z\sin \alpha +x\cos \alpha \end{gathered}$$
这个表达式对应到矩阵$R_y(\alpha )$中，就是我们看到的那个样子。

我们有许多方式来表达三维空间中的旋转。除了上述围绕着固定的轴 x 、y、z 旋转的矩阵外，我们还有其他的公式来表示围绕着过原点的任意轴$n$旋转$\alpha$角度这种情况。这个公式叫 Rodrigues’ Rotation Formula，即罗德里格旋转公式。公式的推导放在了另一篇文章中。

总结一下，三维变换矩阵的大致形式如下：
[ a b c t x d e f t y g h i t z 0 0 0 1 ] \begin{bmatrix} a & b & c & t_x\\ d & e & f & t_y\\ g & h & i & t_z\\ 0 & 0 & 0 & 1 \end{bmatrix}\\ ​adg0​beh0​cfi0​tx​ty​tz​1​ ​

MVP变换

MVP变换中的"MVP" 分别指代 Model、Viewing、Projection，也就是我们经常说的模型变换、视图变换和投影变换，它们是图形学中相对抽象又紧密联系在一起的概念，执行MVP变换的过程，同时也是从建立三维场景到三维场景变为二维图像的过程。

在OpenGL ES 2.0（八）的教程中，我们对冰球进行三维建模，为了计算坐标更加方便，我们默认它的中心位于原点。但是建模完毕之后，我们就不能让它一直呆在那里，而是需要通过平移、旋转等变换把它放在合适的地方。把物体从模型空间变换到世界空间的过程就叫做模型变换。

除了物体，我们当然还需要在三维空间中定义一个相机（或者叫观察者）才能够看到空间中的东西，视图变换指的就是如何摆放这个相机，毕竟不同的位置、不同的角度，我们观察到的场景也不同。

最后，当相机进行拍照，那么三维场景就投影到了二维平面上，我们把这个过程叫做投影变换。

模型变换的基础正是我们在前面几节介绍的平移、旋转等变换，所以下面不再做介绍。我们接下来的重点放在视图变换和投影变换。

视图变换

我们需要考虑对相机下一个定义。显然，在三维空间中的坐标是无法唯一定义一个相机的，因为相机的摄像头可以朝四面八方观察，所以，我们要加上一个向量来表示相机观察的方向。但是这样还不够，相机的观察方向虽然固定了，但是它可以正着拍（快门向上），可以45度斜着拍，甚至180度倒过来拍（快门向下），所以我们要再加一个向量来表示相机的竖直方向（up direction）。总的来说，我们需要三个参数来表示一个相机：

• 相机的位置$e$
• 相机看向（LookAt）的方向$\hat{g}$
• 相机朝上的方向$\hat{t}$

恰好，这几个参数也是我们在 Android SDK 提供的 Matrix 类中构造 LookAt 矩阵时所需要传入的参数：

Matrix.setLookAtM(float[] rm, int rmOffset,
            float eyeX, float eyeY, float eyeZ,
            float centerX, float centerY, float centerZ, float upX, float upY,
            float upZ);

调用这个函数，我们可以得到一个视图变换矩阵（也叫 LookAt 矩阵）。但是，比较违反我们的直觉的事情出现了，这个视图变换矩阵其实是拿来应用在物体上的！

之前我们为了方便解释视图变换的作用，描述了“相机在动物体不动”的场景，因为这很符合我们的直觉。但在图形学的具体实现中，常常规定相机位于空间中一个的固定位置（通常是原点）并看向固定的方向，然后把 “相机移动物体不动” 等价变换为 “相机不动物体移动” 。毕竟，你把相机往左边挪，物体不移动，其实就相当于把物体往右边挪但相机不移动，选择哪种移动方式并不会影响相机观察到的景象。把相机正向移动替换为物体反向移动，进行这样一次反直觉的替换后， LookAt 矩阵就能够像其他的变换矩阵一样，组合到模型变换的矩阵中，这也是不移动相机而要求移动物体的用意所在。

了解了 LookAt 矩阵的前因后果，我们来尝试推导出这个矩阵。我们假设相机的固定位置在坐标原点(0,0,0)处，看向 Z 轴的负半轴，相机朝上的方向为 Y 轴的正方向。

根据我们的常识来说，只要相机和物体没有发生相对运动，那么相机拍下的景象也不会有变化。顺着这个想法，我们假设此时真的有一个相机位于$e$处，看向的方向是$\hat{g}$，朝上的方向是$\hat{t}$。现在，我们得把相机变换到我们假设的固定位置和固定方向，在相机变换的过程中，为了保持相机拍下的景象不变，我们就必须把这个变换同等应用到物体身上。也就是说，把相机从非固定位置变换到固定位置的这个矩阵，就是物体的视图矩阵（LookAt 矩阵）。我们把这个矩阵记为$M_{view}$。

$M_{view}$包含了什么样的基本变换？我们可以分步总结一下：

1. 把相机从位置$e$平移到原点
2. 把$\hat{g}$旋转到 -Z 轴对应的方向
3. 把$\hat{t}$旋转到 Y 轴对应的方向
4. 把$\hat{g}\times \hat{t}$代表的向量旋转到 X 轴对应的方向
   

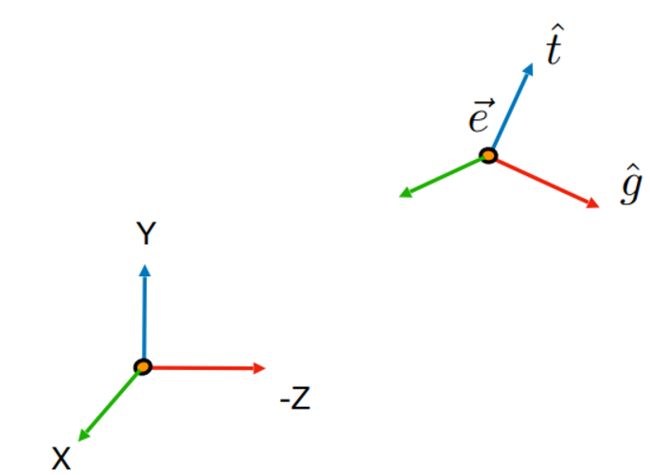
总的来说，完整的视图变换矩阵$M_{view}$包含平移变换$T_{view}$和旋转变换$R_{view}$
$$M_{view}=R_{view}{T}_{view}$$
虽然用了三个小节来说明旋转的效果，但这三个效果对应的是一次旋转变换。简单来说，我们希望用一次旋转令相机的三个方向向量与三个坐标轴同向，这次旋转对应矩阵$R_{view}$。

设$e=(x_e,y_e,z_e)$，我们可以立刻给出$T_{view}$：
T v i e w = [ 1 0 0 − x e 0 1 0 − y e 0 0 1 − z e 0 0 0 1 ] T_{view}=\begin{bmatrix} 1&0&0&-x_e\\0&1&0&-y_e\\0&0&1&-z_e\\0&0&0&1\\ \end{bmatrix} Tview​= ​1000​0100​0010​−xe​−ye​−ze​1​ ​
难题在于我们怎么表达$R_{view}$，我们之前讨论的旋转矩阵都是基于角度的，而现在我们除了$\hat{g}、\hat{v}$的值之外，不知道任何角度信息。我们当然可以使用向量点乘来计算$\hat{g}、\hat{v}$与坐标轴的夹角，但我们有更简单的方法来获得$R_{view}$：先计算$R_{view}$的逆变换矩阵$R_{view}^{-1}$，再求矩阵$R_{view}^{-1}$的逆来得到$R_{view}$。

$R_{view}^{-1}$代表了这样一种变换：把 X 轴旋转到$g\times t$、Y 轴旋转到$t$ 、Z 轴旋转到$-g$的方向。把坐标轴变换到某个向量所指的方向是非常简单的，比如下面的矩阵就可以帮我们把 X轴 (1, 0, 0) 变换到$g\times t$
[ x g ⃗ × t ⃗ y g ⃗ × t ⃗ z g ⃗ × t ⃗ ] = [ x g ⃗ × t ⃗ 0 0 y g ⃗ × t ⃗ 0 0 z g ⃗ × t ⃗ 0 0 ] [ 1 0 0 ] \begin{bmatrix} x_{\vec{g}\times\vec{t}}\\ y_{\vec{g}\times\vec{t}}\\ z_{\vec{g}\times\vec{t}} \end{bmatrix}= \begin{bmatrix} x_{\vec{g}\times\vec{t}}&0&0\\ y_{\vec{g}\times\vec{t}}&0&0\\ z_{\vec{g}\times\vec{t}}&0&0 \end{bmatrix} \begin{bmatrix}1\\0\\0\end{bmatrix} ​xg ​×t ​yg ​×t ​zg ​×t ​​ ​= ​xg ​×t ​yg ​×t ​zg ​×t ​​000​000​ ​ ​100​ ​
仿照上面的思路，我们不难给出完整的$R_{view}^{-1}$，因为我们仍使用齐次坐标，所以$R_{view}^{-1}$是一个4x4的矩阵：
R v i e w − 1 = [ x g ⃗ × t ⃗ x t x − g 0 y g ⃗ × t ⃗ y t y − g 0 z g ⃗ × t ⃗ z t z − g 0 0 0 0 1 ] R_{view}^{-1}= \begin{bmatrix} x_{\vec{g}\times\vec{t}} &x_t & x_{-g} & 0\\ y_{\vec{g}\times\vec{t}} & y_t & y_{-g} & 0\\ z_{\vec{g}\times\vec{t}} & z_t & z_{-g} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} Rview−1​= ​xg ​×t ​yg ​×t ​zg ​×t ​0​xt​yt​zt​0​x−g​y−g​z−g​0​0001​ ​
我们离最后的结果近在咫尺，只要能够求出$R_{view}^{-1}$的逆矩阵，就顺利得到$R_{view}$了。但你不用着急去翻阅线性代数课本，面对这个矩阵，我们会用一种简单的方式来求它的逆。但是要想理解这种方式，我们就需要对正交矩阵做一个介绍。

正交矩阵

让我们先复习一下矩阵转置的含义。简单来说，求矩阵的转置就是把矩阵的行和列调换。一个 2x3 的矩阵进行转置后，会得到一个 3x2 的矩阵。我们用 T 来表示求转置
[ 1 2 3 4 5 6 ] T = [ 1 4 2 5 3 6 ] \begin{bmatrix}1&2&3\\4&5&6\end{bmatrix}^T=\begin{bmatrix}1&4\\2&5\\3&6\end{bmatrix} [14​25​36​]T= ​123​456​ ​
再比如，二维旋转矩阵$R(\alpha )$的转置矩阵等于
$$R^T(\alpha )=\left[\begin{array}{cc}\cos \alpha & \sin \alpha \\ -\sin \alpha & \cos \alpha \end{array}\right]$$
同时，我们来想想$R(\alpha )$的逆矩阵$R^{-1}(\alpha )$是什么。绕着原点旋转$\alpha$角的反面不就是旋转$-\alpha$角吗？所以$R^{-1}(\alpha )=R(-\alpha )$。我们列出矩阵$R(-\alpha )$如下：
$$R(-\alpha )=\left[\begin{array}{cc}\cos (-\alpha )& -\sin (-\alpha )\\ \sin (-\alpha )& \cos (-\alpha )\end{array}\right]=\left[\begin{array}{cc}\cos \alpha & \sin \alpha \\ -\sin \alpha & \cos \alpha \end{array}\right]$$
然后我们惊讶地发现$R^{-1}(\alpha )=R(-\alpha )=R^T(\alpha )$。这说明如果想获得旋转矩阵的逆矩阵，我们只需要求旋转矩阵的转置矩阵即可。一个矩阵的转置等于它的逆，我们把拥有这样的性质的矩阵称作正交矩阵。而无论是二维旋转矩阵，还是三维旋转矩阵，它们都是正交矩阵。

---

旋转矩阵是正交矩阵意味着我们可以轻松求出$R_{view}^{-1}$的逆：
( R v i e w − 1 ) − 1 = ( R v i e w − 1 ) T = [ x g ⃗ × t ⃗ y g ⃗ × t ⃗ z g ⃗ × t ⃗ 0 x t y t z t 0 x − g y − g z − g 0 0 0 0 1 ] (R^{-1}_{view})^{-1}=(R^{-1}_{view})^T= \begin{bmatrix} x_{\vec{g}\times\vec{t}} & y_{\vec{g}\times\vec{t}} & z_{\vec{g}\times\vec{t}} & 0\\ x_t & y_t & z_t & 0\\ x_{-g} & y_{-g} & z_{-g} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} (Rview−1​)−1=(Rview−1​)T= ​xg ​×t ​xt​x−g​0​yg ​×t ​yt​y−g​0​zg ​×t ​zt​z−g​0​0001​ ​
最终我们得到了视图变换矩阵的完全体：
M v i e w = [ x g ⃗ × t ⃗ y g ⃗ × t ⃗ z g ⃗ × t ⃗ − x e x t y t z t − y e x − g y − g z − g − z e 0 0 0 1 ] M_{view}= \begin{bmatrix} x_{\vec{g}\times\vec{t}}&y_{\vec{g}\times\vec{t}} & z_{\vec{g}\times\vec{t}}&-x_e\\ x_t&y_t&z_t&-y_e\\ x_{-g}&y_{-g}&z_{-g}&-z_e\\ 0 & 0 & 0 & 1 \end{bmatrix} Mview​= ​xg ​×t ​xt​x−g​0​yg ​×t ​yt​y−g​0​zg ​×t ​zt​z−g​0​−xe​−ye​−ze​1​ ​

投影变换

经过了模型变换和视图变换之后，物体已经摆放在了正确的位置上，最后一步要做的就是利用投影变换，把三维的场景转换成二维图像。投影有两种不同的方式：正交投影（Orthographic Projection）和透视投影（Perspective Projection），下图展示了这两种投影方式的区别：

在两种不同的投影方式下，我们在 Near clip plane （近平面）内看到的图像并不一样。透视投影遵循“近大远小”的准则，离 Camera 越远的物体看上去越小，这种视觉效果更贴近于我们的生活经验；正交投影则与之相反，不管物体离得有多远，进行正交投影后它们看上去都一样大。我们可以通过观察者到场景的距离来理解这两种投影方式的差异。对于透视投影，我们认为观察者离三维场景比较近， 因此，光线呈放射状汇聚到观察点；对于正交投影，我们认为观察者离场景无限远，光线以平行的状态被我们观察到。

无论采用哪一种投影方式，我们都规定，只有夹在近平面和远平面构成的几何体内的三维场景才是可见的，比如说在上面的示意图中，位于几何体外的绿色的小球就是不可见的。

两种投影方式的变换目标都是相同的：把近远平面构成的几何体正规化，变换成在 NDC 坐标范围内的正方体。所谓的 NDC (normalized device coordinates) 坐标是指 x、y、z 坐标完全在$[-1,1]$的区间内，而这三个方向上的 边界值 -1 和 1 构成了一个正方体。

正交投影

如前面的图所示，在正交投影中，近平面和远平面的面积完全相等，它们构成了一个长方体。我们可以用上、下、左、右、前、后（ $t、b、l、r、f、n$），这几个方位的坐标来定义这个长方体。由于在OpenGL ES 2.0（五）我们给出过关于正交投影的推导，因此这里不再详细推导，我们直接给出结论：
M o r t h o = [ 2 r − l 0 0 − r + l r − l 0 2 t − b 0 − t + b t − b 0 0 2 n − f − n + f n − f 0 0 0 1 ] M_{ortho}=\begin{bmatrix}\frac{2}{r-l} & 0 & 0 & -\frac{r+l}{r-l} \\ 0 & \frac{2}{t-b} & 0 & -\frac{t+b}{t-b}\\ 0 & 0 & \frac{2}{n-f} & -\frac{n+f}{n-f}\\ 0 & 0 & 0 & 1\end{bmatrix} Mortho​= ​r−l2​000​0t−b2​00​00n−f2​0​−r−lr+l​−t−bt+b​−n−fn+f​1​ ​
上面的矩阵并不难理解。想要把一个长方体变成位于$[-1,1]$内的正方体，我们只需要做两件事：先把长方体的所有棱长缩放为2，然后把它的中心平移到原点。因此上面的矩阵包含了缩放变换和平移变换两个部分的内容。

透视投影

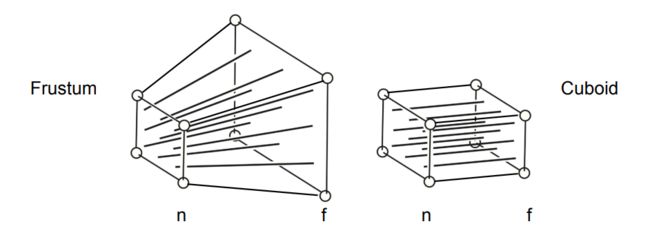
如前面的图所示，在透视投影中，我们把近平面和远平面之间形成的几何体叫做视锥体（frustum）。

因为视锥体不太规则，所以把它变换成正方体确实具有一定的难度。我们当时在教程OpenGL ES 2.0（六）给出了关于透视投影的推导，这份推导的思路是直接把视锥体映射到正方体上。当然可以直接这样证明，代价是理解起来更困难，也可以把“视锥体 -> 正方体”的过程拆解为两步：第一步，我们压缩远平面的大小，把整个视锥体变成长方体（对应矩阵$M_{persp->ortho}$）；第二步，对第一步得到的长方体使用正交投影，得到 NDC 正方体。（对应矩阵$M_{ortho}$）那么透视投影的变换矩阵$M_{persp}=M_{ortho}{M}_{persp->ortho}$

总之，不管你打算采用哪种方式来推导透视投影的矩阵，都会得到类似下面的结果：
[ a a s p e c t 0 0 0 0 a 0 0 0 0 − f + n f − n − 2 f n f − n 0 0 − 1 0 ] \begin{bmatrix} \frac{a}{aspect} & 0 & 0 & 0\\ 0 & a & 0 & 0\\ 0 & 0 & -\frac{f+n}{f-n} & -\frac{2fn}{f-n}\\ 0 & 0 & -1 & 0 \end{bmatrix} ​aspecta​000​0a00​00−f−nf+n​−1​00−f−n2fn​0​ ​
我们来解释一下上面的矩阵。表示近、远平面的坐标的参数为 n 和 f 。参数$a=\frac{1}{\tan (垂直视角角度/2)}$，参数 aspect=近平面的宽高比。这两个参数不太直观，但你只需要理解成这两个参数规定了近平面这个长方形的长和宽就可以了。

正方体到Viewport

在投影变换中，我们得到了一个$[-1,1{]}^3$的正方体，这一个小节是用来说明这个正方体如何映射到 viewport 的。对于 OpenGL 来说，这一步是 OpenGL 具体实现自动完成的，不需要我们来操作，这里仅仅是说明概念。

你可以把 viewpoint 简单理解成在屏幕上的显示区域，之前的 OpenGL 教程中我们调用的glViewport()函数就是用来改变它的大小的，一般它的大小以像素为单位。

把$[-1,1{]}^3$的正方体放进 viewport 中，也就是说把它二维化之前，我们需要进行一次变换，但这次变换只影响 x 和 y 分量。变换矩阵如下：
[ w i d t h 2 0 0 w i d t h 2 0 h e i g h t 2 0 h e i g h t 2 0 0 1 0 0 0 0 1 ] \begin{bmatrix} \frac{width}{2} & 0 & 0 & \frac{width}{2}\\ 0 & \frac{height}{2} & 0 & \frac{height}{2}\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} ​2width​000​02height​00​0010​2width​2height​01​ ​
width 和 height 指代 viewport 的宽度和高度。

虽然二维化了，但是原来的 z 分量并非毫无用处，它将在深度测试中派上用场。

Refer

3维旋转矩阵推导与助记