OpenGL ES 2.0 for Android教程（五）：调整屏幕的宽高比

OpenGL ES 2 第五章：调整屏幕的宽高比

文章传送门

OpenGL ES 2.0 for Android教程（一）

OpenGL ES 2.0 for Android教程（二）

OpenGL ES 2.0 for Android教程（三）

OpenGL ES 2.0 for Android教程（四）

OpenGL ES 2.0 for Android教程（六）

OpenGL ES 2.0 for Android教程（七）

OpenGL ES 2.0 for Android教程（八）

OpenGL ES 2.0 for Android教程（九）

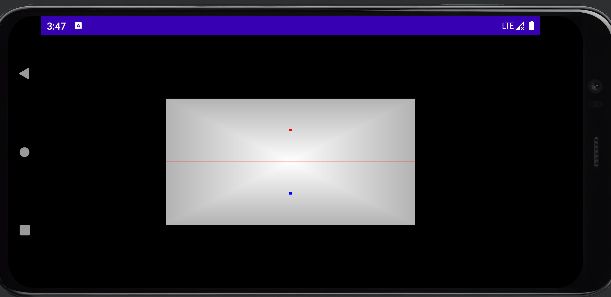
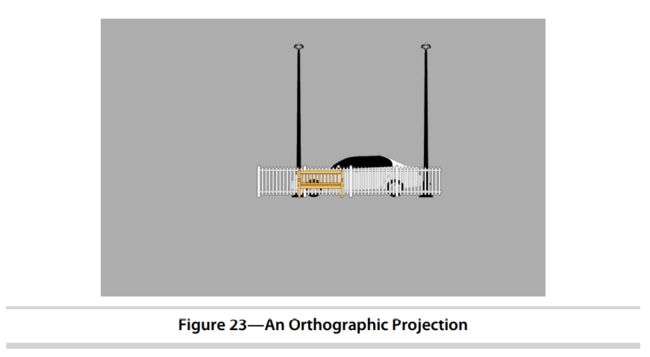
你可能还没有注意到，我们目前的空气曲棍球桌存在竖屏切换到横屏时的比例问题。在横屏下，桌子看起来就像这样：

我们的桌子在横屏时被压扁了！之所以会发生这种情况，是因为我们一直将坐标直接传递到OpenGL，而没有补偿屏幕的宽高比。每个2D和3D应用程序都有一个大问题：它如何决定在屏幕上显示什么，以及它们如何根据屏幕尺寸进行调整？这个问题有一个常用的解决方案：在OpenGL中，我们可以使用投影将世界的一部分映射到屏幕上，可以以这样一种方式进行映射，使它在不同的屏幕大小和方向上看起来都是正确的。由于设备种类繁多，因此能够适应所有设备非常重要。

在本章中，我们将学习为什么我们的桌子会被压扁，以及如何使用投影来解决这个问题。以下是我们的计划：

• 首先，我们将回顾一些基本的线性代数，学习如何将矩阵和向量相乘。

• 然后我们将学习如何定义和使用一个矩阵投影，这将使我们能够补偿屏幕的方向，从而使我们的桌子看起来不会被压扁。

应用存在横竖屏适配问题

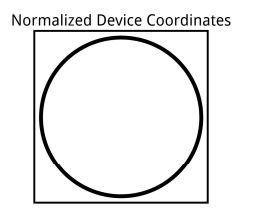
我们现在非常熟悉这样一个事实：我们在OpenGL中渲染的所有内容都会在x轴和y轴上映射到[-1,1]的范围；z轴也是如此。该范围内的坐标称为标准化设备坐标（normalized device coordinates或NDC），与屏幕的实际大小或形状无关。不幸的是，由于它们独立于实际屏幕尺寸，如果直接使用它们，我们可能会遇到问题。

假设我们的实际设备分辨率是1280 x 720像素，这是新安卓设备上的常见分辨率（指的是2013年的情况）。让我们暂时假设OpenGL的内容显示在整个屏幕上，因为这将使讨论变得更容易。

如果我们的设备处于竖屏状态，在[-1，1]的OpenGL坐标跨度下，绝对高度和绝对宽度都为2，高度此时实际跨越了1280个像素，但宽度只跨越了720个像素。因此在绝对视角下边长为2的正方形，显示在屏幕上时，真实图像将沿x轴压平形成长方形。我们之前画的空气曲棍球桌就是经典示例，我们设置的坐标是(0.5, 0.5)、(-0.5, -0.5)、(-0.5, 0.5)、(0.5, -0.5)，看起来应该是个正方形对不对？可是我们在屏幕上看到的是长方形。如果我们处于横向模式，y轴上也会出现同样的问题。

标准化设备坐标假定坐标空间为正方形，如下图所示：

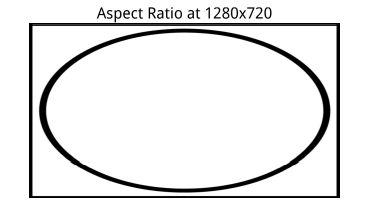
但是，由于实际的viewport 可能不是正方形，图像将在一个方向拉伸，在另一个方向挤压。在标准化设备坐标中定义的图像在竖屏（portrait）设备上看到时会被水平挤压：

在横屏下，相同的图像会以另一种方式被挤压：

调整宽高比例

我们需要调整坐标空间，以便将屏幕形状考虑在内，一种方法是将较小的范围固定为[-1,1]，并根据屏幕尺寸比例调整较大的范围。

例如，在竖屏中，宽度为720，而高度为1280，因此我们可以将宽度范围保持在[-1,1]，并将高度范围调整为[-1280/720,1280/720]或[-1.78,1.78]。我们也可以在横屏下做同样的事情，宽度范围设置为[-1.78,1.78]，高度范围设置为[-1,1]。

通过调整现有的坐标空间，我们最终将改变现有的可用空间，这样，对象在竖屏和横屏下看起来都一样：

使用虚拟坐标空间

为了根据屏幕方向来调整坐标空间，我们不打算再直接给出一个标准化设备坐标，我们开始尝试构建一个虚拟坐标空间，然后，我们需要找到某种方法将虚拟空间中的坐标转换回标准化的设备坐标，以便OpenGL能够正确地渲染它们。这种转换应该考虑屏幕方向，这样我们的空中曲棍球桌在纵向和横向模式下都会正确显示。

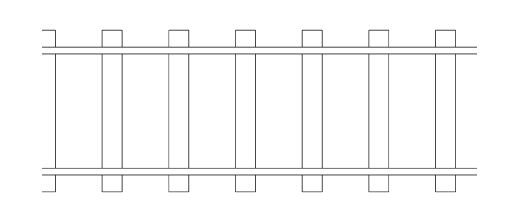
我们要做的工作可以称之为正交投影。使用正交投影时，无论距离远近，所有对象的大小始终相同。为了更好地理解这种投影的作用，假设我们的场景中有一组火车轨道。这是直接从头顶俯瞰时看到的轨迹：

还有一种特殊的正交投影称为等轴测投影( isometric projection )，它是从侧面角度显示的正交投影。这种类型的投影可以用来重建经典的3D角度，就像在一些城市模拟和战略游戏中看到的那样。

从虚拟坐标到标准化设备坐标

当我们使用正交投影从虚拟坐标转换回标准化设备坐标时，我们实际上是3D世界中定义一个区域。该区域内的所有内容都将显示在屏幕上，该区域外的所有内容都将被剪裁。在下图中，我们可以看到一个带有封闭立方体的简单场景。

当我们使用正交投影矩阵将这个立方体映射到屏幕上时，我们将看到下图：

通过正交投影矩阵，我们可以改变这个立方体的大小，这样我们可以在屏幕上看到更多或更少的场景。我们也可以改变这个立方体的形状来补偿屏幕的宽高比例。

在开始使用正交投影之前，我们需要复习一些基本的线性代数。

在本章之后，我们将会经常与矩阵打交道，务必复习一下线性代数。

线性代数回顾

很多OpenGL都使用向量和矩阵，而矩阵最重要的用途之一就是建立正交投影和透视投影。其中一个原因是，使用矩阵进行投影的核心是一系列按顺序对一组数据进行“加法”和“乘法”，而现代GPU在这方面的计算速度非常、非常快。

让我们回到你高中或大学时，复习线性代数的基础知识。如果你不记得了，有不好的回忆，或者从来没有上过课，没有必要担心；我们一起复习基础数学。一旦我们理解了基本的数学知识，我们将学习如何使用矩阵进行正交投影。

向量

向量是元素的一维数组。在OpenGL中，位置或颜色通常是四元素向量。在OpenGL中我们使用的大多数向量通常有四个元素。更一般地来说，向量是一种特殊的矩阵。在下面的示例中，我们可以看到一个带有x、y、z和w分量的位置向量。
$$\left[\begin{array}{c}x\\ y\\ z\\ w\end{array}\right]$$
我们将在第6章中更详细地解释w分量。

矩阵

矩阵是二维元素数组。在OpenGL中，我们通常使用矩阵来使用正交投影或透视投影来投影向量，我们还可以使用它们来旋转、平移和缩放对象。这是通过将矩阵与每个要变换的向量相乘来实现的。

下面是一个矩阵示例。
$$\left[\begin{array}{cccc}{x}_x& x_y& x_z& x_w\\ y_x& y_y& y_z& y_w\\ z_x& z_y& z_z& z_w\\ w_x& w_y& w_z& w_w\end{array}\right]$$

矩阵的行数与列数不一定相等，上方示例的4x4矩阵又被称作4阶矩阵或4阶方阵。

由于方阵在OpenGL中更为常用，因此下文的“矩阵”一般指方阵。

矩阵-向量乘法

要将一个向量与一个矩阵相乘，我们把矩阵放在左边，向量放在右边。然后我们从矩阵的第一行开始，将该行的第一个分量与向量的第一个分量相乘，将该行的第二个分量与向量的第二个分量相乘，依此类推。然后，我们将该行的所有结果相加，以创建结果的第一个部分。

以下是完整的矩阵-向量乘法的示例：
$$\left[\begin{array}{cccc}{x}_x& x_y& x_z& x_w\\ y_x& y_y& y_z& y_w\\ z_x& z_y& z_z& z_w\\ w_x& w_y& w_z& w_w\end{array}\right]\left[\begin{array}{c}x\\ y\\ z\\ w\end{array}\right]=\left[\begin{array}{c}{x}_{x}x+x_{y}y+x_{z}z+x_{w}w\\ y_{x}x+y_{y}y+y_{z}z+y_{w}w\\ z_{x}x+z_{y}y+z_{z}z+z_{w}w\\ w_{x}x+w_{y}y+w_{z}z+w_{w}w\end{array}\right]$$
对于第一行，我们将$x_x$和$x$、$x_y$和$y$、$x_z$和$z$、$x_w$和$w$相乘，然后将所有四个结果相加，以创建结果的$x$分量。

矩阵第一行的所有四个分量将影响结果x，第二行的所有四个分量将影响结果y，依此类推。在矩阵的每一行中，第一个分量与向量的x相乘，第二个分量与y相乘，依此类推。我们会发现，矩阵乘向量得出的结果依然是一个向量。

单位矩阵

让我们看一个包含实际数字的例子。我们将从一个非常基本的矩阵开始，称为单位矩阵。单位矩阵如下所示：
$$\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$
之所以称之为单位矩阵，是因为这个矩阵与任何向量相乘，我们总能得到相同的向量，就像我们将任何数字乘以1得到相同的数字一样。你可以试着乘一乘。

使用矩阵进行平移变换

了解单位矩阵之后，让我们看看OpenGL中经常使用的一种非常简单的矩阵：平移变换矩阵。使用这种矩阵，我们可以沿着指定的距离移动一个对象。这个矩阵看起来就像一个单位矩阵，只不过在右边指定了三个额外的元素：

$$\left[\begin{array}{cccc}1& 0& 0& x_{translation}\\ 0& 1& 0& y_{translation}\\ 0& 0& 1& z_{translation}\\ 0& 0& 0& 1\end{array}\right]$$

让我们来看一个位置向量为（2，2，0，1）的示例（OpenGL中z默认为0，w默认为1），我们想把向量沿x轴平移3，沿y轴平移3，所以我们将把3作为$x_{translation}$和$y_{transation}$，而$z_{translation}$设为0。运算过程如下：
$$\left[\begin{array}{cccc}1& 0& 0& 3\\ 0& 1& 0& 3\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}2\\ 2\\ 0\\ 1\end{array}\right]=\left[\begin{array}{c}2+0+0+3\\ 0+2+0+3\\ 0+0+0+0\\ 0+0+0+1\end{array}\right]=\left[\begin{array}{c}5\\ 5\\ 0\\ 1\end{array}\right]$$
一番操作之后得到了我们期望的结果（5，5，0，1）

变换成功原因是我们从一个单位矩阵出发建立了这个矩阵，所以首先会发生的事情是，原始向量会被复制过来。由于平移分量乘以w，我们通常将位置的w分量指定为1（请记住，如果我们不指定w分量，OpenGL会默认将其设置为1），因此平移分量会被添加到结果中。

这里需要注意w的影响。在下一章中，我们将学习透视投影，在这种投影之后，坐标的w值可能不为1。如果我们在做了投影之后，试图用这个坐标做一个平移或其他类型的变换，而w分量不再是1，那么我们就会遇到麻烦，绘制结果将变形。

我们对向量和矩阵数学的了解刚好足够，让我们继续学习如何定义正交投影。

定义正交投影

为了定义正交投影，我们使用Matrix类，它位于 android.opengl 包中。在该类中有一个名为orthoM()的静态方法，它将为我们生成正交投影。我们将使用该投影来调整坐标空间，很快我们就会发现，正交投影非常类似于平移矩阵。

让我们看看orthoM()的所有参数：

orthoM(float[] m, int mOffset, float left, float right, float bottom, float top, float near, float far)

参数	介绍
float[] m	存储输出结果的数组。该数组的长度应至少为16个元素，以便存储正交投影矩阵。
int mOffset	把结果写入数组m的时候，从该偏移量mOffset开始写入
float left	x轴的最小值
float right	x轴上的最大值
float bottom	y轴的最小值
float top	y轴上的最大值
float near	z轴的最小值
float far	z轴上的最大值

当我们调用此方法时，它会生成以下正交投影矩阵：
$$\left[\begin{array}{cccc}\frac{2}{right-left}& 0& 0& -\frac{right+left}{right-left}\\ 0& \frac{2}{top-bottom}& 0& -\frac{top+bottom}{top-bottom}\\ 0& 0& \frac{-2}{far-near}& -\frac{far+near}{far-near}\\ 0& 0& 0& 1\end{array}\right]$$
不要让分式吓到你：这与我们之前看到的平移变换矩阵非常相似。这个正交投影矩阵将左右、底部和顶部、近距离和远距离之间的所有内容都映射到标准化设备坐标中的[-1,1]范围内，而该范围内的所有内容都将显示在屏幕上。它们的主要区别在于，正交投影矩阵的z轴上有一个负号，这具有反转z坐标的效果，负号的存在完全是因为历史和传统。

当我们把x、y、z轴的最大值固定为1，最小值固定为-1，我们可以获得一个与单位矩阵几乎一致的矩阵，除了z轴取负反转。

以下是正交投影矩阵为什么是我们看到的这个样子的简单解释。

我们首先考虑，如何将一个位于$[left,right]$的坐标x映射到$[-1,1]$。首先，$[left,x]$也是一段区间，我们可以计算区间$[left,x]$与区间$[left,right]$的长度之比，长度之比反映出坐标x的相对区间位置。计算长度之比可以得出算式$\frac{x-left}{right-left}$。

得出x的相对位置之后，接下来需要还原成区间$[-1,1]$的绝对位置，我们仍可以把$[-1,x]$视为一段区间，我们可以笃定，$[-1,x]$与$[-1,1]$的长度之比区间$[left,x]$与区间$[left,right]$的长度之比相等，因此若想得出区间$[-1,x]$的长度，我们只需要使用区间$[-1,1]$的长度乘以比例：$\frac{x-left}{right-left}\times 2$。最后，我们想知道x的位置，只需要加上区间$[-1,x]$的左边界即可。
$$\begin{gathered} x相对于[-1,1]的位置=\frac{x-left}{right-left}\times 2+(-1) \\ =\frac{2x-2left}{right-left}+\frac{left-right}{right-left} \\ =\frac{2x-(right+left)}{right-left} \end{gathered}$$
巧了，我们再试着计算一下上述正交投影矩阵的第一个分量试试？
$$\left[\begin{array}{cccc}\frac{2}{right-left}& 0& 0& -\frac{right+left}{right-left}\\ 0& \frac{2}{top-bottom}& 0& -\frac{top+bottom}{top-bottom}\\ 0& 0& \frac{-2}{far-near}& -\frac{far+near}{far-near}\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]$$

$$第一个分量=\frac{2x}{right-left}+(-\frac{right+left}{right-left})$$

实质上，我们可以以这样一种角度来理解矩阵乘法：矩阵乘法相当于把我们上述的变换过程换成矩阵方式来进行表达。

左手坐标系与右手坐标系

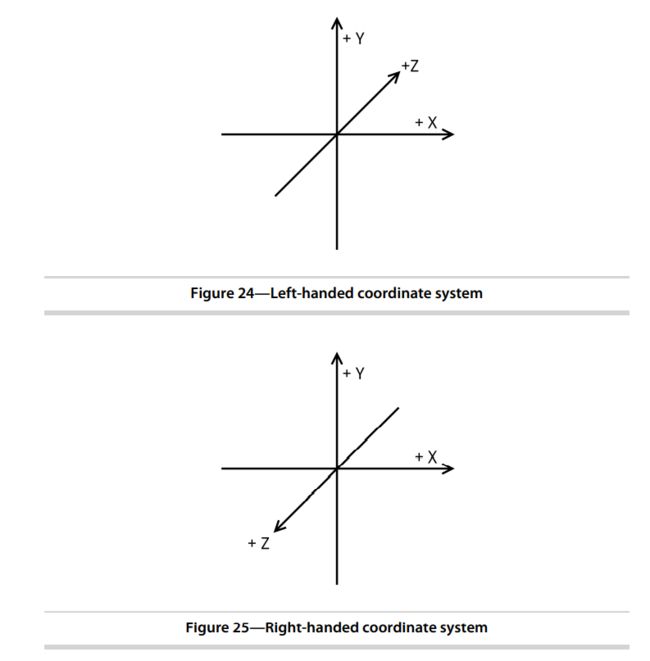
为了更好地理解z轴的问题，我们需要理解左手坐标系（left-handed coordinate）和右手坐标系（ right-handed coordinate）之间的区别。要确定坐标系是左手坐标系还是右手坐标系，请用一只手，将大拇指指向正x轴。然后食指指向y轴正方向。

现在，将中指指向z轴。如果你用左手来做这件事，那么你看到的是左手坐标系。如果你使用右手，那么这是一个右手坐标系。

下面的图片分别展示了左手坐标系和右手坐标系，与通常看到的Z轴竖直朝上的坐标系不同，图中的坐标系Y轴固定朝上：

使用左手坐标系还是右手坐标系其实并不重要，只是一个惯例问题。虽然标准化设备坐标使用左手坐标系，但在早期版本的OpenGL中（这里指的是OpenGL 1.0版本，尚不允许编写Shader的那时候），其他所有坐标系默认使用右手坐标系，而左手坐标系与右手坐标系差异出现在z轴的朝向，这就是为什么Android的Matrix默认情况下会生成反转z的矩阵。

如果您希望在其他地方也使用左手坐标系，而不仅仅是在标准化的设备坐标中，那么您可以撤销orthoM()在z轴上的反转。

现在我们对矩阵数学有了基本的了解，我们准备在代码中添加正交投影。

添加正交投影

让我们更新我们的代码，添加一个正交投影，并修复被压扁的桌子。

更新着色器代码

我们需要做的第一件事是更新着色器，以便它使用我们的矩阵来变换我们的位置向量。更新simple_vertex_shader.glsl 的代码：

uniform mat4 u_Matrix;

attribute vec4 a_Position;
attribute vec4 a_Color;

varying vec4 v_Color;

void main() {
    v_Color = a_Color;

    gl_Position = u_Matrix * a_Position;
    gl_PointSize = 10.0;
}

我们添加了一个新的uniform变量u_Matrix，类型为为mat4，这意味着这个变量代表一个4x4矩阵。我们还修改了gl_Position的赋值语句，现在我们将矩阵与位置向量相乘，这里的乘法代表着矩阵乘法。现在，我们的顶点数组不再被解释为标准化设备坐标，而是被解释为存在于被矩阵定义的虚拟坐标空间中——矩阵的作用就是把这个虚拟坐标空间中的坐标转换回标准化的设备坐标。

添加矩阵数组与矩阵变量位置

我们添加一个常量来储存u_Matrix变量的名称，然后再添加两个类变量，用来存储矩阵与u_Matrix变量的位置。

// 未列出完整代码
class AirHockeyRenderer(private val context: Context): GLSurfaceView.Renderer {
    ...
    
    private val projectionMatrix: FloatArray = FloatArray(16)
    /**
     * 缓存u_Matrix的位置
     */
    private var uMatrixLocation = 0
    
    override fun onSurfaceCreated(gl: GL10?, config: EGLConfig?) {
        ...
        uMatrixLocation = glGetUniformLocation(programId, U_MATRIX)
        ...
    }
    
    companion object {
        ...
        private const val U_MATRIX = "u_Matrix"
    }
}

创建正交投影矩阵

在onSurfaceChanged()中添加以下代码：

override fun onSurfaceChanged(gl: GL10?, width: Int, height: Int) {
    glViewport(0, 0, width, height)
    // 是否为横屏
    val isLandscape = width > height
    val aspectRatio = if (isLandscape) (width.toFloat()) / (height.toFloat()) else
                    (height.toFloat()) / (width.toFloat())
    if (isLandscape) {
        orthoM(projectionMatrix, 0, -aspectRatio, aspectRatio, -1f, 1f, -1f, 1f)
    } else {
        // 竖屏或正方形屏幕
        orthoM(projectionMatrix, 0, -1f, 1f, -aspectRatio, aspectRatio, -1f, 1f)
    }
}

上述代码将创建一个正交投影矩阵，这个矩阵会考虑屏幕的当前方向，建立起一个虚拟坐标空间。Android中有不止一个Matrix类，所以你需要确保你导入的是android.opengl.Matrix。

首先，我们计算宽高比，取宽度和高度中的较大值，除以宽度和高度中的较小值，这样的话可以保证无论我们是在横屏还是竖屏这个值都是相同的。

然后我们调用方法orthoM()。如果我们处于横屏，我们就应当视y轴的坐标空间为$[-1,1]$，然后去扩展x轴的坐标空间。（当屏幕旋转了之后，x轴和y轴的方向也会随着窗口旋转，或者换句话说，x轴和y轴的方向是相对于窗口的。）这样x轴上的坐标将能够从$[-aspectRatio,aspectRatio]$映射到$[-1,1]$，而y轴不需要映射。如果处于竖屏，我们就需要扩展y轴的坐标空间，而x轴保持原样即可。

把矩阵数据发送给着色器

最后一个修改是把正交投影矩阵发送到着色器，我们onDrawFrame()添加以下代码：

override fun onDrawFrame(gl: GL10?) {
    glClear(GL_COLOR_BUFFER_BIT)
    glUniformMatrix4fv(uMatrixLocation, 1, false, projectionMatrix, 0)
}

我们来稍微解释一下glUniformMatrix4fv()的参数。

glUniformMatrix4fv(int location, int count, boolean transpose, float[] value, int offset)

参数	介绍
int location	uniform变量的位置
int count	需要修改的矩阵的个数
boolean transpose	指明矩阵是列优先矩阵还是行优先矩阵，列优先矩阵应传入false
float[] value	表示矩阵的一维数组
int offset	偏移量

一维数组表示矩阵有两种方式，列优先矩阵和行优先矩阵，顾名思义，行优先就是把矩阵的行向量依次排列在数组中的意思，列优先同理。

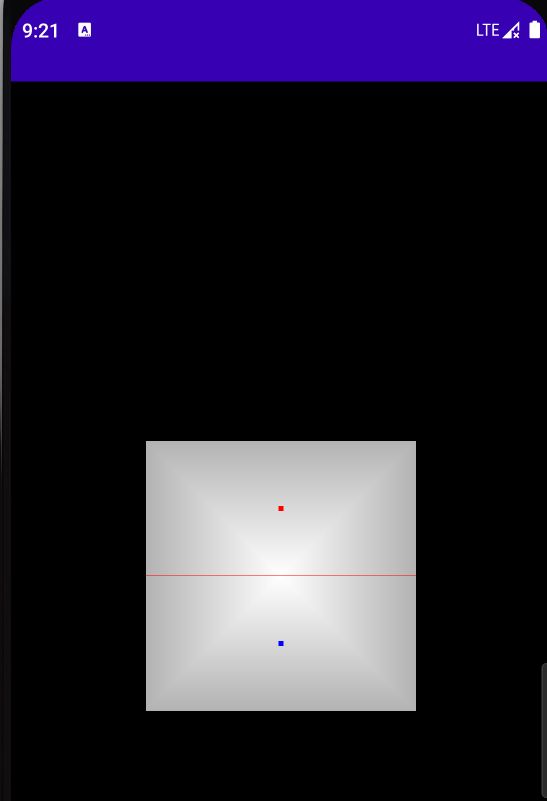
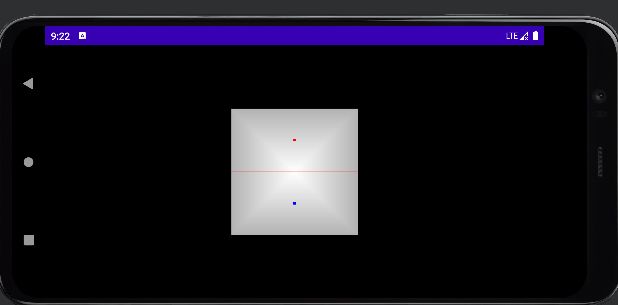
目前的运行效果

再次更新顶点的位置

现在的坐标终于符合我们一般的直觉，四个坐标（0.5，0.5）、（0.5，-0.5）（-0.5，-0.5）、（-0.5，0.5）围成的终于是一个正方形了，但是我们不想要一个正方形的桌子，所以我们稍微修改一下顶点的位置：

private val tableVerticesWithTriangles: FloatArray = floatArrayOf(
    // 属性的顺序: X, Y, R, G, B
    // 三角形扇形
    0f, 0f, 1f, 1f, 1f,
    -0.5f, -0.8f, 0.7f, 0.7f, 0.7f,
    0.5f, -0.8f, 0.7f, 0.7f, 0.7f,
    0.5f, 0.8f, 0.7f, 0.7f, 0.7f,
    -0.5f, 0.8f, 0.7f, 0.7f, 0.7f,
    -0.5f, -0.8f, 0.7f, 0.7f, 0.7f,
    // 中线
    -0.5f, 0f, 1f, 0f, 0f,
    0.5f, 0f, 1f, 0f, 0f,
    // 两个木槌
    0f, -0.4f, 0f, 0f, 1f,
    0f, 0.4f, 1f, 0f, 0f
)

运行效果可以自行验证。

本章小结

我们花时间学习了线性代数背后的一些基础知识，并用它来理解矩阵与向量相乘时会发生什么。然后我们学习了如何定义正交投影矩阵，它允许我们重新定义坐标空间，我们使用这个矩阵来修复从竖屏旋转到横屏时产生的失真。

如果矩阵数学的任何部分看起来不清楚，请回头再看一遍”线性代数回顾“一节。从这里到本书的结尾，我们将花费越来越多的时间研究向量和矩阵！

练习

尝试调整正交投影矩阵，使桌子显示得越来越大、越来越小，并在屏幕上四处平移。要实现这一点，您需要调整传递给orthoM()的left, right, top,bottom这些值。

一旦你完成了这些练习，准备好抓牢你的椅子，因为我们将进入第三维度。