OpenGL ES 2.0 for Android教程（六）：进入第三维

OpenGL ES 2 第六章：进入第三维

文章传送门

OpenGL ES 2.0 for Android教程（一）

OpenGL ES 2.0 for Android教程（二）

OpenGL ES 2.0 for Android教程（三）

OpenGL ES 2.0 for Android教程（四）

OpenGL ES 2.0 for Android教程（五）

OpenGL ES 2.0 for Android教程（七）

OpenGL ES 2.0 for Android教程（八）

OpenGL ES 2.0 for Android教程（九）

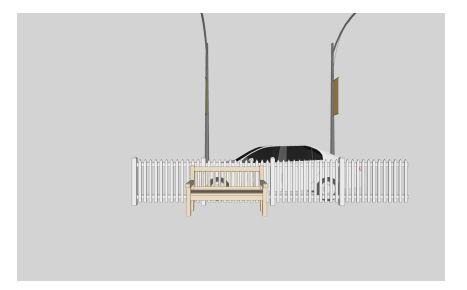
想象一下，你现在位于游戏厅，站在一张曲棍球桌前，望着另一端的对手。从你的角度来看，这张桌子会是什么样子？你这一端的桌子会显得更大，你以一个较低的角度俯视桌子，而不是直接从正上方俯视。毕竟，没有人打一场桌上冰球的时候是站在桌子上往下看的。

虽然OpenGL非常擅长在2D中渲染东西，但当我们添加第三个维度的坐标时，屏幕中的内容就更灿烂了。在这一章中，我们将学习如何进行3D渲染，这样我们就可以获得在桌子对面俯视对手的视觉感受。

以下是本章的计划：

• 首先，我们将学习OpenGL的透视除法（perspective division），以及如何使用w分量在2D屏幕上创建3D效果。
• 一旦我们理解了w分量，我们将学习如何设置透视投影（perspective projection），以便我们可以看到3D版本的桌子。

从三维艺术出发

几个世纪以来，艺术家使用过诸多技巧愚弄人们的眼睛，让他们把平面的二维绘画视为一个完整的三维场景。他们使用的一个技巧叫做线性投影（linear projection）—— 通过将平行线连接在一个假想的消失点上来创造透视的错觉。

当我们站在一对笔直的铁轨上时，我们可以看到这种效果的典型例子；当我们看向远方的铁轨时，它们似乎越来越近，直到消失在地平线上的一个点上：

随着离我们越来越远，铁路枕木似乎也变得越来越小。如果我们测量每根枕木的表观尺寸，它们的测量尺寸会随着它们与我们眼睛的距离成比例地减小。这个技巧就是创建真实3D投影所需的秘诀，让我们继续学习该如何使用OpenGL做到这一点。

将着色器坐标转换到屏幕

我们现在已经熟悉了标准化设备坐标（NDC），知道为了在屏幕上显示顶点，其x、y和z分量都需要在[-1,1]的范围内。让我们查看以下流程图，看看坐标是如何从顶点着色器写入的原始gl_Position转换到屏幕上的最终坐标的：

gl_Position

标准化设备坐标

窗口实际坐标

start

透视除法

视口变换

end

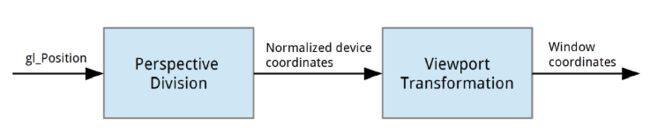
上图展现了两个转换步骤和三个不同的坐标空间。

裁剪空间

当顶点着色器将值写入gl_Position时，OpenGL希望该位置位于裁剪空间（Clip Space）中。裁剪空间背后的逻辑非常简单：对于任何给定位置，x、y和z分量都需要在该位置的-w和w之间。例如，如果位置的w定为1，则x、y和z分量都需要介于-1和1之间。任何超出此范围的内容都不会显示在屏幕上。

其他分量取决于w分量的原因在我们学习了透视除法之后就会很明显了。

透视除法

在顶点位置成为标准化设备坐标之前，OpenGL实际上会执行一个额外的步骤，称为透视除法（perspective division）。透视除法执行后，位置将在标准化设备坐标中，其中每个可见坐标的x、y和z分量的都将位于[-1,1]范围内，而不管渲染区域的大小或形状如何。

为了在屏幕上创建3D效果，OpenGL会获取每个gl_Position，并将x、y和z分量除以w分量。当使用“w”分量表示距离时，距离更远的对象将被移动到更靠近渲染区域中心的位置，渲染区域的中心此时便起到了消失点的作用。这就是OpenGL如何使用艺术家几个世纪以来一直使用的相同技巧来欺骗我们，让我们仿佛看到3D场景的原理。

例如，假设某个物体有两个顶点，每个顶点都在3D空间中的相同位置，具有相同的x、y和z分量，但具有不同的w分量。假设这两个坐标是（1,1,1,1）和（1,1,1,2）。在OpenGL使用这些作为标准化设备坐标之前，它将进行一次透视除法，并将前三个组件除以w。现在每个坐标的划分如下：（1/1，1/1，1/1）和（1/2，1/2，1/2）。经过此划分后，标准化设备坐标将为（1,1,1）和（0.5,0.5,0.5）。w较大的坐标移近（0,0,0），即渲染区域的中心（在标准化设备坐标中）。

在下图中，我们可以看到这种效果的一个例子，随着w值的增加，具有相同x、y和z的坐标将越来越靠近中心：

在OpenGL中，3D效果是线性的，并沿直线完成。在现实生活中，事情要复杂得多（想象一下鱼眼镜头），但这种线性投影是一种合理的近似。

注：鱼眼镜头（Fisheye lens）是一种超广角镜头。

齐次坐标

由于透视除法，裁剪空间中的坐标通常被称为齐次坐标（homogenous coordinates）（齐次坐标的概念由August Ferdinand Möbius于1827年引入）。它们被称为齐次的原因是裁剪空间中的多个坐标可以映射到同一点。例如，以以下几点为例：

(1, 1, 1, 1), (2, 2, 2, 2), (3, 3, 3, 3), (4, 4, 4, 4), (5, 5, 5, 5)

进行透视除法后，这些点都将映射到标准化设备坐标中的（1,1,1）。

除以W的优点

你可能想知道为什么我们不简单地除以z。毕竟，如果我们将z解释为距离，并且有两个坐标，（1,1,1）和（1,1,2），那么我们可以除以z得到两个标准化坐标（1,1）和（0.5,0.5）。

虽然这是可行的，但添加w作为第四个组件有其他优势。我们可以将透视效果与实际的z坐标解耦，这样就可以在正交投影和透视投影之间切换。保留z分量作为深度缓冲区（depth buffer）还有一个好处，我们将在后面章节的”用深度缓冲区移除隐藏曲面“来介绍这一点。

视口变换

在我们看到最终结果之前，OpenGL需要将标准化设备坐标的x和y分量映射到屏幕上的一个区域内，这个区域是操作系统留出的用于显示的区域，被称作视口（viewport），这些映射的坐标称为窗口坐标。除了告诉OpenGL如何进行映射之外，我们不需要太关心这些映射坐标。我们目前通过在onSurfaceChanged()中调用glViewport()来设置viewport的大小。当OpenGL进行这种映射时，它会将（-1，-1，-1）到（1，1，1）的范围映射到为显示而预留的窗口。超出此范围的标准化设备坐标将被剪裁。

添加W分量以创建透视图

如果我们实际看到w分量的作用，那么就能更容易理解它的效果，所以让我们把它添加到我们的顶点数据中，看看会发生什么。由于我们现在将指定位置的x、y、z和w分量，因此我们首先需要更新POSITION_COMPONENT_COUNT常量，然后再次更新顶点数组，如下所示：

private val tableVerticesWithTriangles: FloatArray = floatArrayOf(
    // 属性的顺序: X, Y, Z, W, R, G, B
    // 三角形扇形
    0f, 0f, 0f, 1.5f, 1f, 1f, 1f,
    -0.5f, -0.8f, 0f, 1f, 0.7f, 0.7f, 0.7f,
    0.5f, -0.8f, 0f, 1f, 0.7f, 0.7f, 0.7f,
    0.5f, 0.8f, 0f, 2f, 0.7f, 0.7f, 0.7f,
    -0.5f, 0.8f, 0f, 2f, 0.7f, 0.7f, 0.7f,
    -0.5f, -0.8f, 0f, 1f, 0.7f, 0.7f, 0.7f,
    // 中线
    -0.5f, 0f, 0f, 1.5f, 1f, 0f, 0f,
    0.5f, 0f, 0f, 1.5f, 1f, 0f, 0f,
    // 两个木槌
    0f, -0.4f, 0f, 1.25f, 0f, 0f, 1f,
    0f, 0.4f, 0f, 1.75f, 1f, 0f, 0f
)
companion object {
    private const val POSITION_COMPONENT_COUNT = 4
    ...
}

我们在顶点数据中添加了一个z和一个w分量。我们已经更新了所有顶点，使屏幕底部附近的顶点w为1，而屏幕顶部附近的顶点w为2；我们还更新了中线和木槌，使其具有介于两者之间的分数w。这会使桌子的顶部看起来比底部小，就好像我们从一端望向另一端一样。我们把所有的z分量都设置为零，因为不需要在z分量有任何值就能获得立体效果。

OpenGL将自动使用我们指定的w值为我们进行透视除法，我们当前的正交投影只会复制这些w值。让我们继续运行我们的项目，看看它是什么样子：

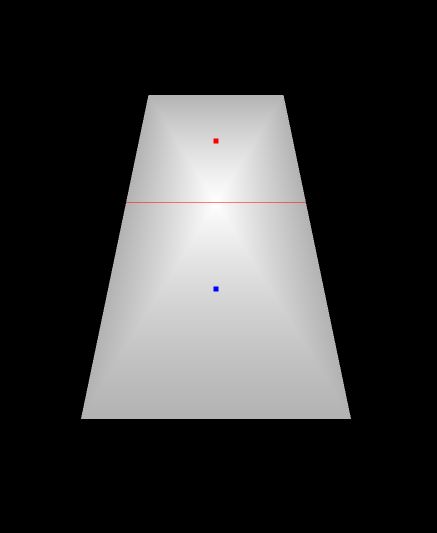
桌子看起来有点立体感了！我们只需要指定w就可以做到这一点。然而，如果我们想获得更加动态的效果，比如改变桌子的角度或放大缩小，该怎么办？我们应当使用矩阵为我们生成值，而不是硬编码w值。让我们还原刚才对顶点和常量的更改。在下一节中，我们将学习如何使用透视投影矩阵自动生成w值。

转为使用透视投影

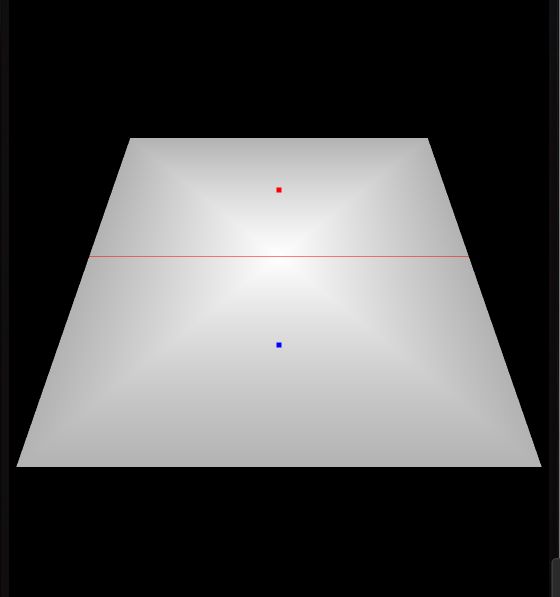
在我们进入透视投影背后的矩阵数学之前，让我们从视觉层面来讨论一下。在前一章中，我们使用正交投影矩阵，通过调整转换为标准化设备坐标的区域的宽度和高度来补偿屏幕的宽高比。

在下图中，我们把正交投影可视化为一个包围整个场景的立方体，表示OpenGL最终将在视口上渲染的内容，也是我们能够看到的内容：

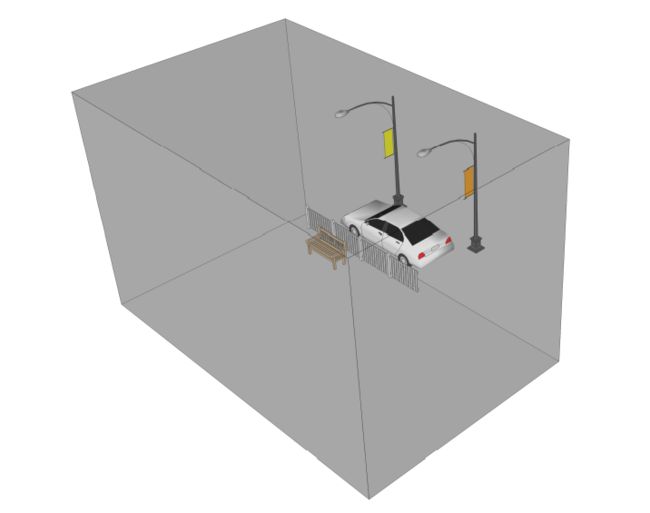
不同的视角显示相同的场景：

视锥体

当我们切换到投影矩阵时，场景中的平行线会在屏幕上的一个消失点相交，物体将随着距离越来越远而变得越来越小。我们所看到的空间区域不再是立方体，而与下图“通过视锥体的投影”更为相似。

这种形状被称为视锥体（frustum），这个观察空间是通过透视投影矩阵和透视除法创建的。所谓的frustum就是通过让原来的正方体的远侧的一面变得比近侧更大，从而令它变成视锥体的形状。两面大小差异越大，视角就越广，我们能看到的就越多。

视锥体还拥有一个焦点（focal point）。这个焦点可以通过延长视锥体的两条侧棱来得到，它们相交的点就是焦点。当您使用透视投影查看场景时，这个场景看起来就像你的视角被放在了这个焦点上。焦点和视锥体较小的面之间的距离称为焦距，这影响了视锥体小端和大端与相应视角之间的比例。

在下图中，我们可以从焦点处看视锥体内的场景：

焦点的另一个有趣特性是，在焦点上观察，视锥体两端在屏幕上似乎占据了面积相同的空间。（想一想那个延长线你就能明白为什么看起来“面积相等”）。视锥体的远端更大，但由于距离更远，它占用的空间反而与近端相同。这和日食的原理相似：月球比太阳小得多，但因为它离我们近得多，所以它看起来大得足以遮住太阳。

定义透视投影

为了重现3D的魔力，我们的透视投影矩阵需要与透视除法一起工作。投影矩阵本身不能进行透视除法，透视除法需要某些东西才能起作用。

随着一个物体离我们越来越远，它应该向屏幕的中心移动，大小也相应减小，所以我们的投影矩阵最重要的任务是为w创建合适的值，这样当OpenGL进行透视除法时，远的物体会比近的物体显得更小。其中一种方法是将z分量定义为物体与焦点之间的距离，然后将该距离映射到w。距离越大，w越大，生成的对象越小。

“透视投影背后的数学”一节位于本文附录，该节将对透视投影矩阵进行推导，如果读者已经对透视矩阵熟稔于心，完全可以忽略这一节的内容。

调整宽高比和视角

透视投影矩阵如下，它允许我们调整视角的同时调整屏幕宽高比：
$$\left[\begin{array}{cccc}\frac{a}{aspect}& 0& 0& 0\\ 0& a& 0& 0\\ 0& 0& -\frac{f+n}{f-n}& -\frac{2fn}{f-n}\\ 0& 0& -1& 0\end{array}\right]$$
下面是对该矩阵中定义的变量的快速解释：

变量	解释
a	这个变量代表焦距。焦距由$\frac{1}{\tan(Y轴视角角度/2)} $计算，视角必须小于180度。例如，当视角为90度时，焦距将等于1。
aspect	屏幕的宽高比，即宽度/高度。
f	坐标原点距离较远的平面的距离，这个值必须为正且大于距离近平面的距离。
n	坐标原点与较近的平面的距离，这个值必须为正。例如，如果将其设置为1，则近平面将位于z=-1的位置。

随着视角变小，焦距变长，映射到归一化设备坐标中的范围[-1,1]所对应的x和y也相应减小。这会使视锥体变窄。

在下图中，左侧的视锥体的视角为90度，而右侧的视锥体的视角为45度：

可以看到，对于45度的视锥体，焦点和近平面之间的焦距稍长。

以下是两个视锥体各自从焦点上看到的场景：

在视角较窄的情况下，通常很少出现失真问题。另一方面，随着视角变宽，最终图像的边缘将扭曲得更严重。在现实生活中，较宽的视角会使一切看起来都是弯曲的，就像在相机上使用鱼眼镜头时看到的效果一样。由于OpenGL使用沿直线的线性投影，最终的图像会被拉伸。

在代码中创建投影矩阵

现在，我们准备向代码中添加透视投影。我们可以使用Android中的Matrix类的perspectiveM()方法，也可以创建自己的方法来实现上一节中定义的矩阵，下面来实现一个与perspectiveM()非常类似的方法。

在util包中创建MatrixHelper 类：

object MatrixHelper {
    fun perspectiveM(m: FloatArray, yFovInDegrees: Float, aspect: Float, n: Float, f: Float) {
        // TODO
    }
}

我们要做的第一件事是基于y轴上的视角来计算焦距。在方法签名之后添加以下代码：

// 计算弧度制的角度
val angleInRadians = (yFovInDegrees * Math.PI / 180.0).toFloat()
// 计算焦距
val a = (1.0 / tan(angleInRadians / 2.0)).toFloat()

我们使用Java的Math类来计算正切值，因为它需要以弧度为单位的角度，所以我们将视角从度转换为弧度，然后计算焦距。接下来我们输出矩阵结果：

m[0] = a / aspect
m[1] = 0f
m[2] = 0f
m[3] = 0f
m[4] = 0f
m[5] = a
m[6] = 0f
m[7] = 0f
m[8] = 0f
m[9] = 0f
m[10] = -((f + n) / (f - n))
m[11] = -1f
m[12] = 0f
m[13] = 0f
m[14] = -((2f * f * n) / (f - n))
m[15] = 0f

这会将矩阵数据写入参数m中定义的浮点数组，该数组至少需要16个元素。OpenGL以列优先顺序来存储矩阵数据，这意味着开始的四个值指的是第一列，接下来的四个值指的是第二列，依此类推。

我们现在已经完成了perspectiveM()，并准备在代码中使用它。我们的方法与Matrix源代码中的方法非常相似，只是做了一些细微的更改，使其更具可读性。

切换到投影矩阵

现在我们将转而使用透视投影矩阵。打开AirHockeyRenderer并从onSurfaceChanged()中删除所有代码，只保留对glViewport()的调用，然后添加以下代码：

MatrixHelper.perspectiveM(projectionMatrix, 55f, width.toFloat() / height.toFloat(), 1f, 10f)

这将创建一个垂直视角为55度的透视投影矩阵。视锥体将以$z=-1$为近平面，$z=-10$为远平面。

添加MatrixHelper的导入后，继续运行程序。你可能会注意到我们的曲棍球桌不见了。因为我们没有为桌子指定z分量，所以默认情况下z=0，但是我们视锥体的最近的平面在$z=-1$，我们至少得把它们移动到$z=-1$以后才有可能看到它们。

与其硬编码z值，不如先使用平移矩阵将桌子移出，然后再使用投影矩阵进行投影。按照惯例，我们将这个矩阵称为模型矩阵(Model Matrix)。

使用模型矩阵移动对象

让我们在AirHockeyRenderer添加一个类变量：

/**
 * 模型矩阵
 */
private val modelMatrix = FloatArray(16)

我们将使用这个矩阵将空气曲棍球台移动到远处。在onSurfaceChanged()的末尾，添加以下代码：

Matrix.setIdentityM(modelMatrix, 0)
Matrix.translateM(modelMatrix, 0, 0f, 0f, -2f)

这会将模型矩阵设置为单位矩阵，然后设置沿z轴的平移量为-2。当我们用这个矩阵乘以我们的曲棍球桌坐标时，这些坐标最终会沿着负z轴移动2个单位。（如果忘记如何使用矩阵进行平移变换，参见第五章）

相乘一次还是两次

我们现在要做一次选择：我们需要将模型矩阵应用到每个顶点，所以我们的第一个方案是将额外的矩阵添加到顶点着色器中。我们先将每个顶点乘以模型矩阵，沿负z轴移动2个单位，然后将每个顶点乘以投影矩阵，这个方案的缺点是我们需要再修改一遍代码，声明新的矩阵变量，并把值传递给OpenGL，这些过程稍显繁琐。还有一个更好的方案：我们可以将模型矩阵和投影矩阵相乘，然后将得出的矩阵结果传递给顶点着色器。这样我们就只需要在着色器中保留一个矩阵。

复习矩阵乘法

可能你已经忘记矩阵乘法的规则了，让我们稍微复习一下。矩阵乘法总结起来就是，结果矩阵的第M行N列的结果，由左边矩阵的第M行行向量乘以右边矩阵的第N行列向量得出。下面给出了第二行第三列元素的生成计算式。
$$\left[\begin{array}{cccc}?& ?& ?& ?\\ a_1& a_2& a_3& a_4\\ ?& ?& ?& ?\\ ?& ?& ?& ?\end{array}\right]\left[\begin{array}{cccc}?& ?& b_1& ?\\ ?& ?& b_2& ?\\ ?& ?& b_3& ?\\ ?& ?& b_4& ?\end{array}\right]=\left[\begin{array}{cccc}?& ?& ?& ?\\ ?& ?& a_1{b}_1+a_2{b}_2+a_3{b}_3+a_4{b}_4& ?\\ ?& ?& ?& ?\\ ?& ?& ?& ?\end{array}\right]$$

选择合适的矩阵乘法次序

矩阵乘法并不满足交换律，因为我们左右矩阵取的分别是行向量和列向量，左和右并不对称。因此，矩阵乘法的次序很重要，如果我们搞错了模型矩阵与透视投影矩阵相乘的次序，就很可能什么都看不到。

为了弄清楚我们应该使用哪个顺序，让我们看看两次矩阵映射的计算式：
$$\begin{gathered} verte{x}_{eye}=ModelMatrix\ast verte{x}_{model} \\ verte{x}_{clip}=ProjectionMatrix\ast verte{x}_{eye} \end{gathered}$$
$verte{x}_{model}$表示原始的顶点坐标，经过平移变换之后得到$verte{x}_{eye}$，然后将$verte{x}_{eye}$与投影矩阵相乘得到最终的变换坐标。结合两个表达式，将上面的式子的结果代入下面，我们不难得出以下结论：
$$verte{x}_{clip}=ProjectionMatrix\ast ModelMatrix\ast verte{x}_{model}$$
因此，用一个矩阵替换这两个矩阵时，正确的矩阵相乘的次序应当是$ProjectionMatrix\ast ModelMatrix$，左侧是投影矩阵，右侧是模型矩阵。

更新代码以使用一个矩阵

让我们更新代码，在onSurfaceChanged()调用Matrix.translateM()后添加以下内容：

val temp = FloatArray(16)
// 矩阵相乘
Matrix.multiplyMM(temp, 0, projectionMatrix, 0, modelMatrix, 0)
System.arraycopy(temp, 0, projectionMatrix, 0, temp.size)

将两个矩阵相乘时，我们需要一个临时区域来存储结果。如果我们试图直接写入projectionMatrix，造成的结果是未定义的。

我们首先创建一个浮点数组来存储临时结果；然后我们调用multiplyMM()将投影矩阵和模型矩阵相乘到这个临时数组中。接下来将结果拷贝至projectionMatrix。

如果我们现在运行应用程序，它应该如下图所示。把曲棍球桌推到远处后，它进入了我们透视投影的视锥体，但桌子仍然直立着。在快速回顾一遍所学内容之后，我们将学习如何旋转桌子，以便从一个较低的角度而不是竖直的角度看到它。

A Quick Recap

让我们快速回顾一下我们在过去几节中所讨论的内容：

• 我们学习了如何使用额外的矩阵将空气曲棍球桌移动到屏幕上，然后将其传递到投影矩阵中。
• 我们学习了如何将两个矩阵相乘。
• 然后，我们学习了如何合并投影矩阵和模型矩阵，这样我们就不必修改顶点着色器的代码来接受额外的矩阵。

添加旋转效果

我们已经配置了一个投影矩阵和一个模型矩阵来移动我们的桌子，现在我们希望改变一下看桌子的角度，我们可以使用旋转矩阵来实现这一点。由于我们还没有研究过旋转，所以让我们花一些时间来了解这些旋转是如何工作的。

旋转的方向

在立体空间下旋转要弄清楚的是，我们需要绕哪个轴旋转以及旋转多少角度。为了描述清楚一个物体是如何绕一个给定的轴旋转的，我们将使用右手法则：伸出你的右手，握紧拳头，将你的大拇指指向正轴的方向。其他的手指的弯曲方向向你展示了一个物体在给定一个正旋转角度的情况下，应当往哪个方向进行旋转。例如下面一幅图，当你把大拇指指向正x轴的方向，其余手指的弯曲方向正好是逆时针。

我们现在要做的是绕x轴向后旋转桌子，这样可以赋予桌子层次感。

旋转矩阵

我们将使用旋转矩阵来完成旋转任务。矩阵旋转使用正弦和余弦的三角函数将旋转角度转换为比例因子。以下是绕x轴旋转的矩阵定义：
$$\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& \cos (a)& -\sin (a)& 0\\ 0& \sin (a)& \cos (a)& 0\\ 0& 0& 0& 1\end{array}\right]$$
绕y轴旋转的矩阵如下：
$$\left[\begin{array}{cccc}\cos (a)& 0& \sin (a)& 0\\ 0& 1& 0& 0\\ -\sin (a)& 0& \cos (a)& 0\\ 0& 0& 0& 1\end{array}\right]$$

绕z轴旋转的矩阵如下：
$$\left[\begin{array}{cccc}\cos (a)& -\sin (a)& 0& 0\\ \sin (a)& \cos (a)& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$
还可以基于任意角度和矢量将所有上面提到的矩阵组合成通用旋转矩阵。请注意，上述矩阵仅在左手坐标系生效。

如果读者对旋转矩阵的推导感兴趣，可以跳到后面的”旋转矩阵推导“一节。

将旋转矩阵添加到我们的代码中

现在，我们已经准备好添加旋转效果。让我们修改onSurfaceChanged()的代码，调整平移并添加旋转，如下所示：

override fun onSurfaceChanged(gl: GL10?, width: Int, height: Int) {
    glViewport(0, 0, width, height)
    MatrixHelper.perspectiveM(projectionMatrix, 55f, width.toFloat() / height.toFloat(), 1f, 10f)

    // 调整模型矩阵
    Matrix.setIdentityM(modelMatrix, 0)
    Matrix.translateM(modelMatrix, 0, 0f, 0f, -2.5f)
    Matrix.rotateM(modelMatrix, 0, -60f, 1f, 0f, 0f)
    
    val temp = FloatArray(16)
    // 矩阵相乘
    Matrix.multiplyMM(temp, 0, projectionMatrix, 0, modelMatrix, 0)
    System.arraycopy(temp, 0, projectionMatrix, 0, temp.size)
}

我们旋转桌子的时候底部会离我们更近，因此我们把桌子推得更远了一点。然后，我们将桌子绕x轴旋转-60度，使桌子处于一个良好的角度，就像我们站在它前面一样。

现在桌子看起来应该像下面这样：

本章小结

这是一个包含较多信息的章节。随着我们了解透视投影以及它们如何与OpenGL的透视除法一起工作，矩阵数学变得更加复杂。然后，我们学习了如何使用第二个矩阵移动和旋转桌子。

好消息是，我们不需要完全理解投影和旋转背后的数学和理论，就可以使用它们。只要对什么是视锥体以及矩阵如何帮助我们移动东西有了基本的了解，你就会发现在未来的道路上使用OpenGL要容易得多。

练习

试着调整视野角度，观察对空气曲棍球台的影响。你也可以尝试用不同的方式移动桌子。

一旦你完成了这些练习，我们将开始让我们的桌子看起来更棒。在下一章中，我们将开始使用纹理（texture）。

附录

透视投影背后的数学

参考资料：https://zhuanlan.zhihu.com/p/152280876

如果上面列出的知乎专栏无内容，请转至该作者github文章备份

这篇专栏对透视投影推导讲述的非常细致，值得一读。

本人水平有限，本节的数学知识如有错漏，敬请斧正。

推导透视投影矩阵之前，我们先把基本的几何体给画出来。

绘制视锥体

首先，我们先画出两个与$xoy$平面平行的平面，离原点较近的那个平面到原点距离设为n（near的意思），离原点较远的那个平面到原点的距离为f（far的意思），如下图所示。与经常看到的Z轴朝上的右手坐标系不同，这个右手坐标系的Y轴固定朝上，图中蓝色的轴是z轴，绿色的轴是y轴，红色的轴是x轴。（此时两个平面的方程分别是$z=-n$和$z=-f$）

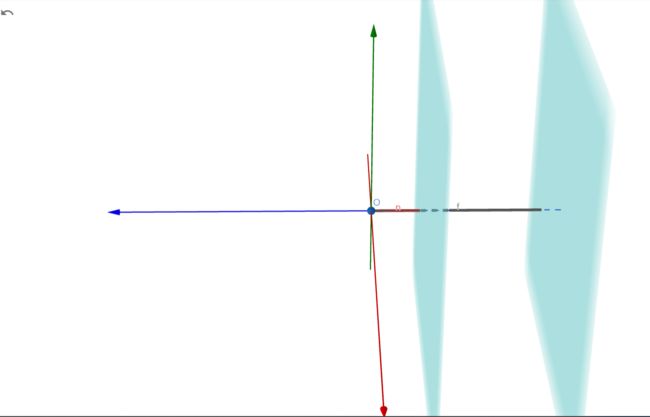
我们绘制的这两个平面将作为视锥体的near平面和far平面。

现在，我们在离原点较近的那个平面（以后简称near平面）上取四个点，构成一个矩形。我们对这个矩形的唯一的要求是，这个矩形的中心点必须在z轴上。不妨假设这四个点分别是ABCD，我们可以得到下图：

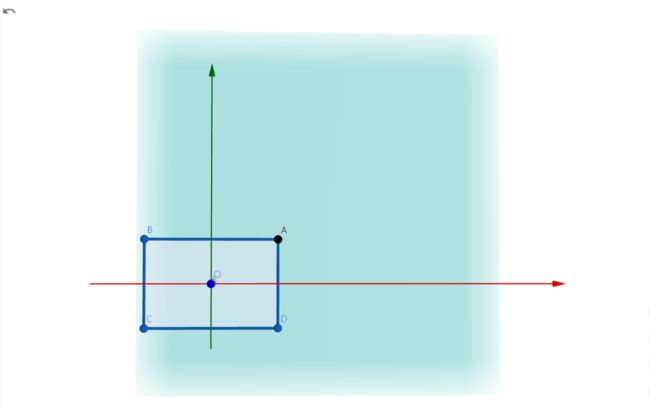
然后，我们分别连接原点O与四个点ABCD，得到OA、OB、OC、OD，我们延长这四条直线，这些直线与平面$z=-f$分别相交于EFGH四点，最后，我们连接EFGH形成矩形，如下图所示：

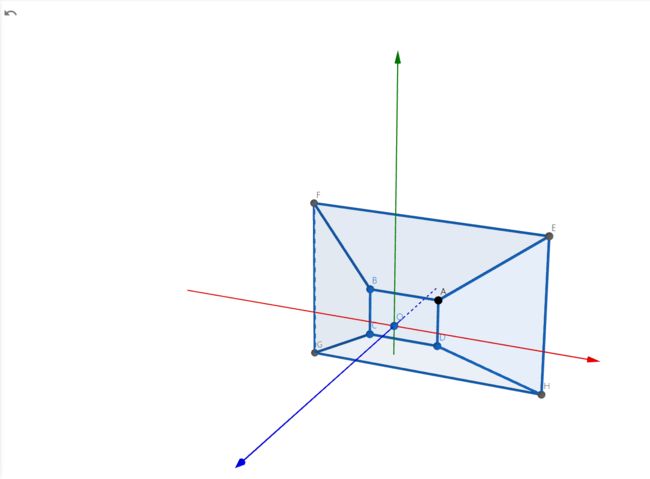
平面ABCD与平面EFGH之间的空间就是我们要的视锥体，其中ABCD是原物体，EFGH是投影之后的物体，O点相当于摄像机位置，我们能看到的所有点都位于蓝色的视锥体内部，换句话说，蓝色的视锥体内部就是我们现在的虚拟坐标空间。

• 为什么视锥体绘制在Z轴负半轴的区域？

  经过之前的学习我们得知NDC（标准化设备坐标）是左手坐标系，而我们上面绘图用的都是右手坐标系，因此我们绘制在Z轴负半轴，因为右手系的Z轴负半轴对于左手系来说，就是Z轴的正半轴。

• 我们画出的视锥体很特殊，它的焦点与坐标原点重合，这更有利于我们进行分析，但请注意焦点不一定需要与坐标原点重合。

• 上文画出的视锥体可在GeoGebra查看，边观察视锥体边阅读效果更佳。

将虚拟坐标还原至NDC

跟第五章类似，我们的虚拟坐标必须经过一些变换才能还原到NDC的[-1,1]坐标范围。我们将独立为x、y、z方向推导这些映射函数。我们需要的映射函数可以概括为输入是x、y、z，而输出必须位于[-1,1]内，而且，我们希望虚拟空间坐标的端点也是NDC的端点，比如说，我们希望虚拟空间坐标的$z=-n$对应NDC的-1，$z=-f$对应NDC的1。

首先，我们先假设出一些变量再进行进一步的讨论：

设$(x_e,y_e,z_e)$表示视锥体中的点在相机坐标系（我们绘图使用的坐标系）的坐标。

设$(x_n,y_n,z_n)$表示$(x_e,y_e,z_e)$经过变换之后得到的NDC下的坐标。

我们不妨先推导z分量的线性映射关系，这个关系很好推导，因为平面ABCD和平面EFGH垂直于Z轴！因此，虚拟坐标的z坐标范围一定是$[-f,-n]$，我们可以把他们很简单地映射到[-1,1]，不过需要注意，平面$z=-n$对应NDC的-1，平面$z=-f$对应NDC的1。我们列出以下式子：
$$z_n=\frac{-z_e-n}{f-n}\cdot 2+(-1)\text{\hspace{1em}(1)}$$

推导x分量的映射

虽然可以假定z分量它使用线性映射关系，可x分量就不是线性的映射关系了，我们不能使用上面的方法来求x的NDC坐标映射。为什么x的映射不是线性的？我们先来看一下视锥体在$zox$平面上的投影，注意z轴和x轴的方向，z轴朝右，x轴朝下，图中那个看不太清楚的是点B：

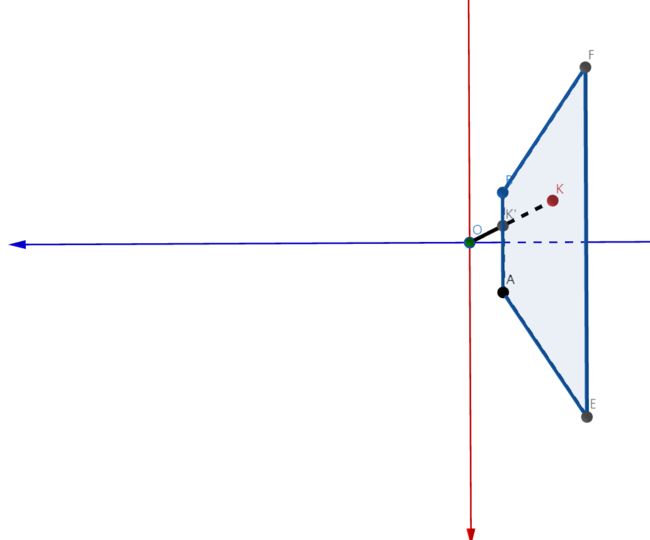
我们注意到，除了B点之外，线段BF上所有点都依赖于点B来“生成”——点O“发出”的一条射线OB把点B的投影照在平面EFGH上，这个过程中生成了线段上的点。因此我们希望，即使点B和点F的$x_e$不同，进行NDC坐标映射之后，点B和点F的$x_n$应当相同，这就是为什么x的映射关系不是线性的。如果点B和点F，或者更广义地说，若在OB射线上的点的$x_n$不同，这就不是透视投影了。

我们解释了为什么x的映射不是线性的。接下来我们考虑如何计算x的映射关系，我们仍然使用上面的图来分析。

我们假设视锥体内有一点K，设K的坐标为$(x_e,y_e,z_e)$，线段$OK$交平面ABCD于点$K^{\prime }$，我们记$K^{\prime }$的坐标为$(x_p,y_p,z_p)$，又因为$K^{\prime }$在平面ABCD上，平面ABCD离O点的距离为n，因此坐标为$K^{\prime }(x_p,y_p,-n)$。

根据三角形相似关系，我们可以得到：
$$\begin{gathered} \frac{z_e}{z_p}=\frac{x_e}{x_p} \\ {x}_p=\frac{-n{x}_e}{z_e} \end{gathered}$$
如果不是很理解哪里来的三角形，可以看下图：

上述步骤相当于我们把点K投影回平面ABCD的点$K^{\prime }$。接下来我们就能再次运用线性关系投影的思路了：我们只要把线段AB除以一个常数使得它们长度为2，不就相当于把它们映射到[-1,1]上面了吗？（线段AB轴对称，因此这是可行的）。列出方程$AB\cdot k=2$，即$k=\frac{2}{AB}$，问题随之而来，我们如何计算AB的长度？

我们可以通过OB、z轴、AB三线”夹出来“的三角形来计算AB的一半长度。我们真正需要知道的参数是OB与z轴形成的夹角$\theta$，然后根据正弦关系，$\frac{AB}{2}=n\tan (\theta )$。接下来立刻可以算出$k=\frac{1}{n\tan (\theta )}$。因此可以得出$x_p$映射到$x_n$的函数
$$x_n=\frac{x_p}{n\tan (\theta )}$$
然后我们就得出了$x_e$到$x_n$的函数，只需要代入之前的计算结果：
$$x_n=-\frac{n{x}_e}{z_e}\frac{1}{n\tan (\theta )}=-\frac{x_e}{z_e\tan (\theta )}$$

视角${\theta }_h$与${\theta }_v$

我们紧急借用了角度$\theta$来推导公式，但是还没有搞清楚$\theta$是什么，现在来解释一下。

在投影图中，$\theta$是OB与z轴形成的夹角，根据轴对称的性质，我们不难发现OC与z轴的夹角也是$\theta$，其实z轴类似于一个角平分线。投影图中的OB和OC的夹角$2\theta$，在三维视图看来实际上是平面$OBC$与平面$OAD$形成的夹角。我们把这个夹角称作水平视角，我们用${\theta }_h$来表示。类似的还有平面$OAB$与平面$OCD$的夹角，我们把它称作垂直视角，用${\theta }_v$来表示。这两个视角限制了横向和纵向的可视范围，在这两个角度之外的点都不会被渲染。

我们重新改写一下$x_e$到$x_n$的映射函数：
$$x_n=-\frac{x_e}{z_e\tan ({\theta }_h/2)}\text{\hspace{1em}(2)}$$
我们不难证明，$\tan ({\theta }_h/2)$与$\tan ({\theta }_v/2)$之间存在比例关系，它们的比例和$AB$、$AD$的边长之比相关：
$$\frac{\tan ({\theta }_h/2)}{\tan ({\theta }_v/2)}=\frac{AB}{AD}$$

推导y分量的映射

因为视锥体沿z轴轴对称，因此，我们不难发现对y分量的推导与对x分量的推导大同小异，因此这里直接给出结果，详细的计算交给读者来进行，可以参考推导x分量映射的过程来进行。

$y_e$映射至$y_n$的函数如下：
$$y_n=-\frac{y_e}{z_e\tan ({\theta }_v/2)}\text{\hspace{1em}(3)}$$

投影…矩阵？

让我们试着把各个分量的函数整合成一个矩阵，我们期望得到一个这样的式子，左边的矩阵包含所有常数的系数，右边则是需要变换的向量，它们相乘之后就成功变换出目标向量。
$$\left[\begin{array}{ccc}\cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot \end{array}\right]\left[\begin{array}{c}{x}_e\\ y_e\\ z_e\end{array}\right]=\left[\begin{array}{c}{x}_n\\ y_n\\ z_n\end{array}\right]$$
我们把标号为（1）、（2）、（3）的式子连立起来：
$$\left[\begin{array}{ccc}-\frac{1}{z_e\tan ({\theta }_h/2)}& 0& 0\\ 0& -\frac{1}{z_e\tan ({\theta }_v/2)}& 0\\ 0& 0& \cdot \end{array}\right]\left[\begin{array}{c}{x}_e\\ y_e\\ z_e\end{array}\right]=\left[\begin{array}{c}{x}_n\\ y_n\\ z_n\end{array}\right]$$
等会，我们的矩阵里面包含的不是常数，而是一个与$z_e$相关的值，这不仅意味着映射是非线性的，更意味着我们使用这种方式无法得到只包含常数的矩阵。矩阵的值只能在与具体的向量相乘时才能确定，这样的矩阵根本起不到什么作用。怎么办？

齐次坐标表示

如果你对齐次坐标还有印象，应该能猜到我们如何解决上面的问题：我们把目标向量改为${\left(\begin{array}{cccc}{w}_n{x}_n& w_n{y}_n& w_n{z}_n& w_n\end{array}\right)}^T$，只要$w_n=-z_e$，即可得到$x_e$到$w_n{x}_n$、$y_e$到$w_n{y}_n$的线性变换，存储常数的矩阵包含$z_e$会令我们很为难，但是包含在目标向量里面，反而可以接受，因为OpenGL稍后可以通过透视除法直接去除$z_e$。我们现在得到一个符合我们要求的矩阵：
$$\left[\begin{array}{cccc}-\frac{1}{\tan ({\theta }_h/2)}& 0& 0& 0\\ 0& -\frac{1}{\tan ({\theta }_v/2)}& 0& 0\\ 0& 0& k& b\\ 0& 0& -1& 0\end{array}\right]\left[\begin{array}{c}{x}_e\\ y_e\\ z_e\\ 1\end{array}\right]=\left[\begin{array}{c}-z_e{x}_n\\ -z_e{y}_n\\ -z_e{z}_n\\ -z_e\end{array}\right]$$
我们终于摆平了$x_e$、$y_e$到$x_n$、$y_n$的映射，随之而来的一个问题就是我们不能使用之前从$z_e$到$z_n$的线性关系，而要重新计算$z_e$到$-z_e{z}_n$的映射了。没错，$z_e$到$z_n$的映射不止一种，还有很多其他的可能，我们现在希望找一种能够和$x_e$、$y_e$一起放在同一个矩阵的映射关系。

你可以观察到我们在矩阵里塞进了两个未知数$k$和$b$，这源于我们的假设，假设从$z_e$到$-z_e{z}_n$的映射函数是一个线性函数，它满足：
$$k{z}_e+b=-z_e{z}_n\text{\hspace{1em}(4)}$$
由于$z_n$表示相机与某点的垂直距离，因此它与$x_e$、$y_e$无关，矩阵第三行前两个数为0。

现在让我们来计算k和b。再次强调，平面$z=-n$对应NDC的-1，平面$z=-f$对应NDC的1，因此当$z_e=-n$时$z_n=-1$，当$z_e=-f$时$z_n=1$。我们把值代入（4）式，可以得到一个方程组：
$$\begin{gathered} \{\begin{array}{r}-nk+b=-n\\ -fk+b=f\end{array} \\ 解得\{\begin{array}{r}k=-\frac{f+n}{f-n}\\ b=-\frac{2fn}{f-n}\end{array} \end{gathered}$$

计算出k和b的值后，我们现在得到这样一个矩阵：
$$\left[\begin{array}{cccc}-\frac{1}{\tan ({\theta }_h/2)}& 0& 0& 0\\ 0& -\frac{1}{\tan ({\theta }_v/2)}& 0& 0\\ 0& 0& -\frac{f+n}{f-n}& -\frac{2fn}{f-n}\\ 0& 0& -1& 0\end{array}\right]$$
我们离最终的透视投影矩阵只差一点点。我们还可以进行一些令矩阵看起来更简洁的优化。首先，我们之前就已经知道了$\tan ({\theta }_h/2)$与$\tan ({\theta }_v/2)$的比值是定值，换个角度想，这意味着，我们只需要知道一个角度就够了，另一个角度的值可以通过简单的乘法获得。我们决定选用垂直视角${\theta }_v$，而${\theta }_h$使用${\theta }_v$来表示：
$$\begin{gathered} \tan (\frac{{\theta }_h}{2})=\frac{AB}{AD}\tan (\frac{{\theta }_v}{2}) \\ 若将宽高比aspect规定为:平行于X轴的AB，除以平行于Y轴的AD \\ 即aspect=\frac{AB}{AD} \\ 则\tan (\frac{{\theta }_h}{2})=aspect\cdot \tan (\frac{{\theta }_v}{2}) \end{gathered}$$
最后，$-\frac{1}{\tan ({\theta }_v/2)}$写起来太费劲，干脆规定$a=-\frac{1}{\tan ({\theta }_v/2)}$，我们可以得到最终化简的透视投影矩阵：
$$\left[\begin{array}{cccc}\frac{a}{aspect}& 0& 0& 0\\ 0& a& 0& 0\\ 0& 0& -\frac{f+n}{f-n}& -\frac{2fn}{f-n}\\ 0& 0& -1& 0\end{array}\right]$$

推导旋转矩阵

概览

我们已经了解了如何使用旋转矩阵（虽然这些矩阵只能绕坐标轴旋转），可这些矩阵为什么长这个样子呢？本节内容将试图给出旋转矩阵的推导过程。

让我们先来看一眼以z轴为旋转轴时的旋转矩阵：
$$\left[\begin{array}{cccc}\cos (a)& -\sin (a)& 0& 0\\ \sin (a)& \cos (a)& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$
我们假想它与向量$[x_a,y_a,z_a,w_a{]}^T$相乘（T是求转置矩阵的意思），显然，变换之后只有x分量和y分量发生了变化，z分量和w分量都不变。设$x_a$、$y_a$为变换前的坐标，$x_b$、$y_b$为变换后的坐标，经过旋转矩阵运算后，我们有：
$$\begin{gathered} x_b=x_a\cos (a)-y_a\sin (a) \\ {y}_b=x_a\sin (a)+y_a\cos (a) \end{gathered}$$
在三维空间绕坐标轴旋转却只涉及两个坐标分量的变换，这启示我们，平面下的旋转变换与这个矩阵肯定有莫大的关系，接下来我们把目光放在二维平面下的旋转。

二维平面下的旋转

首先，选择描述所求问题的方式非常重要。比如，描述“求二维平面下一个点旋转之后的新坐标”这个问题，我们的第一种描述如下：（该坐标系y轴朝上，x轴朝右）

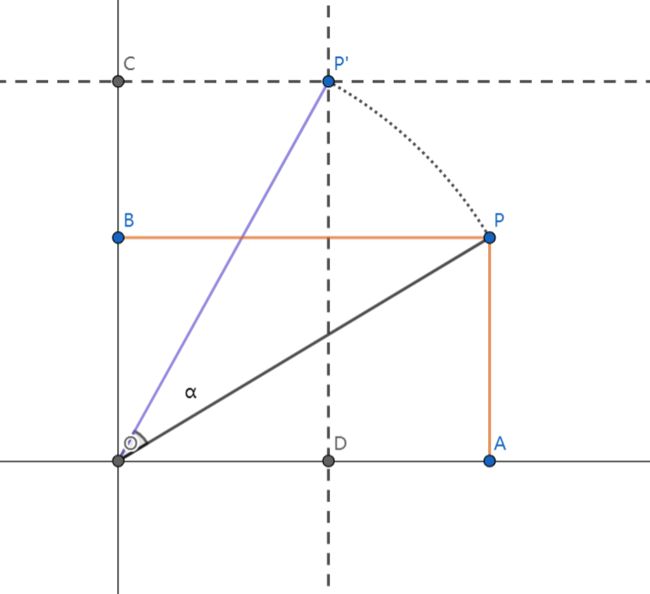
点$P$进行逆时针旋转$\alpha$角度之后，得到点$P^{\prime }$。
$$\begin{gathered} 已知:P点的坐标（即线段OA、OB的长度）和角度\alpha \\ 求:P^{\prime }点的坐标（即线段OC、OD的长度） \end{gathered}$$
别着急求解上面描述的问题，我们还有描述这个问题的另一个方式：

原坐标轴沿逆时针旋转$\alpha$角度后，得到图中用红色的线标注的坐标轴。
$$\begin{gathered} 已知:P点相对于原坐标轴的坐标（即线段OD、OE的长度）和角度\alpha \\ 求:点P在新坐标轴下的坐标（即OG、OH的长度） \end{gathered}$$
第一种描述方式来自于旋转的一般定义；第二种描述方式做了一件不太直观的事情，它令坐标轴旋转而不是令点旋转，我们不难发现，这两种问题描述方式是等价的。但是，第一种方式，也就是我们常识之中存在的方式，实际上很难进行计算。因此，我们最终使用第二种问题描述方式来继续推导。

计算OH的长度

我们先设一些变量方便描述，设P点相对于原坐标轴的坐标为$(x_a,y_a)$，P点在新坐标轴下的坐标为$(x_b,y_b)$，

显然有$OD=x_a,OE=y_a,OH=x_b,OG=y_b$。我们先计算OH的长度。

计算之前，让我们再进行作图，对图形添加一些点和辅助线来辅助我们计算：

首先我们过D点作平行于OH的平行线，并延长PH，直线PH与那条平行线交于A点，然后我们擦掉平行线，保留线段DA即可。然后，我们过D作垂直于OH的垂线，这条垂线与OH交于点B。我们可以看到图中标注了三个直角，并且现在我们形成了两个三角形：三角形APD（蓝色区域）、三角形ODB（绿色区域）。

我们为什么额外绘制这些图形？因为我们想要分割线段OH，你可以发现，现在线段OH=线段OB+线段BH，而BH=DA。

线段DA的长度可以通过简单的三角函数来计算，注意在三角形APD（蓝色区域）内，我们有：
$$DA=DP\sin (\alpha )$$
如果读者不明白为什么可以得出上面的式子，请查看三角函数sin、cos的定义。

又因为线段$DP=OE=y_a$，因此$DA=y_a\sin (\alpha )=BH$。

然后我们观察三角形ODB（绿色区域），有$OB=OD\cos (\alpha )=x_a\cos (\alpha )$，然后我们把OB和BH加起来得到：
$$OH=x_b=x_a\cos (\alpha )+y_a\sin (\alpha )$$

计算OG的长度

计算OG的长度的思路与上面类似，而且我们可以使用上面那张图继续进行计算。

我们注意到OG=PH，而恰巧PH=PA-HA，HA又等于BD。计算过程如下：
$$\begin{gathered} BD=x_a\sin (\alpha )=HA \\ PA=y_a\cos (\alpha ) \\ {y}_b=OG=PH=PA-HA=y_a\cos (\alpha )-x_a\sin (\alpha ) \end{gathered}$$

微妙的差异

我们发现$x_b$和$y_b$的运算式与之前根据旋转矩阵正向推导的式子存在微妙的差异，这其实是因为我们为了讨论的方便而将坐标轴逆时针旋转，事实上，对应于点逆时针旋转的坐标轴的操作，应当是将坐标轴顺时针旋转，也就是说上述计算结果需要取负角度，化简后即可得到原旋转矩阵的结果。

最后

如果对三维空间下的旋转问题特别感兴趣，可以搜索“欧拉角”、“四元数”等关键词。