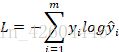吴恩达深度学习第二课第三周作业及学习心得体会 ——softmax、batchnorm

写在前面

本周课程用了两周完成，因为课程让用tensorflow实现，编码时还是更希望自己手写代码实现，而在实现过程中，低估了batchnorm反向计算的难度，导致算法出现各种bug，开始是维度上的bug导致代码无法运行，等代码可以运行时，训练神经网络的时候成本又总会发散，于是静下心来把整个运算的前向和反向过程认真推导了好几遍，期间参考网上一些资料，但感觉都没有把问题真正说清楚，连续三天的推导后，才找到了问题的本质，现将自己写的代码汇总如下。

softmax

概念

softmax相对来说比较简单。其用于处理多元分类问题，而之前学习回归时就在思考怎么解决多元分类问题，并无师自通的实现了onehot编码和hardmax（也是学习softmax时才明白之前实现的是onehot编码和hardmax回归）……

回归模型是Logistic回归模型在多分类问题上的推广，在多分类问题中，输出y的值不再是一个数，而是一个多维列向量，有多少种分类是就有多少维数。激活函数使用的是softmax函数：

损失函数变为：

其反向传播求导公式即为：。注意该公式指的是（代码中写为dZ），而不是！

代码

库：

import numpy as np
import matplotlib.pyplot as plt

训练集数据代码：

'''**********************************************************************'''
#产生数据
def gendata():
    np.random.seed(1)
    m = 3600                                #样本数
    N = int(m/2)                            #分为两类
    D = 2                                   #样本的特征数或维度
    X = np.zeros((m,D))                     #初始化样本坐标
    y = np.zeros((m,1))                     #初始化样本标签
    Y = np.zeros((m,3))                     #初始化样本标签
    a = 1.5                                 #基础半径
    
    for j in range(12):
        if j<6:   
            ix = range((m//12)*j, (m//12)*(j+1))
            t = np.linspace((3.14/3)*j+0.01, (3.14/3)*(j+1)-0.01, m//12) #theta角度
            r = a + np.random.randn(m//12)*0.15                          #radius半径
            X[ix] = np.c_[r*np.sin(t), r*np.cos(t)]                      #生成坐标点
            y[ix] = j%3
            '''
            if j%3==0:
                Y[ix] = [1,0,0]
            if j%3==1:
                Y[ix] = [0,1,0]
            if j%3==2:
                Y[ix] = [0,0,1]
            '''
        else:
            ix = range((m//12)*j, (m//12)*(j+1))
            t = np.linspace((3.14/3)*j+0.01, (3.14/3)*(j+1)-0.01, m//12) #theta角度
            r = a*2 + np.random.randn(m//12)*0.15                        #radius半径
            X[ix] = np.c_[r*np.sin(t), r*np.cos(t)]                      #生成坐标点
            y[ix] = (j+1)%3
            '''
            if j%3==0:
                Y[ix] = [0,1,0]
            if j%3==1:
                Y[ix] = [0,0,1]
            if j%3==2:
                Y[ix] = [1,0,0]
            '''
        Y = np.eye(3)[np.int32(y).reshape(-1)]                          #该语句实现的功能与上面注释部分相同
    return X.T,Y.T,y.T

绘出图形如下：

单次前向函数，删除sigmoid函数（可以不删除……），增加softmax函数，注意np.sum(np.exp(Z),axis=0)，是对np.exp(Z)求和，axis=0表示按行求和，计算出来的向量应该是(1,m)，即对每个样本列里的元素求和；

'''**********************************************************************'''
#单次前向运算
def single_forward(A_pre, W, b, mode):
    Z = np.dot(W, A_pre) + b        #根据上一层的输出A_pre，以及本层的W b计算本层的Z
    
    if mode=='softmax':             #根据所选定的激活函数计算本层的输出
        A = np.exp(Z)/np.sum(np.exp(Z),axis=0)   #np.sum(np.exp(Z),axis=0),是对np.exp(Z)求和，axis=0表示按行求和，计算出来的向量应该是(1,m)
    if mode=='ReLU':
        A = (Z+abs(Z))/2
    if mode=='tanh':
        A = np.tanh(Z)
        
    cache = {'A_pre':A_pre,
             'W':W,
             'b':b,
             'Z':Z,
             'A':A}
    
    return cache

前向传播函数中第L层，调用sigmoid改为调用softmax；

'''**********************************************************************'''
#前向传播函数
def prop_forward(X, parameters,lambd):
    caches = []
    L = len(parameters)//2
    
    for l in range(1,L+1):          #l从1到L，调用L次前向运算
        
        W = parameters['W'+str(l)]
        b = parameters['b'+str(l)]
        
        if l==1:                    #第一次运算时，A_pre=X
            A_pre = X
            L2_SUM = 0
        else:
            A_pre = cache['A']
            L2_SUM = L2_SUM + 0.5*lambd*np.sum(W*W) 
        if l==L:                    #最后一次运算时，激活函数为sigmoid
            mode = 'softmax'
        else:
            mode = 'tanh'
              
        cache = single_forward(A_pre, W, b, mode)
        caches.append(cache)
        
    AL = caches[L-1]['A']
    
    return AL, caches, L2_SUM

单次后向函数，对第L层的softmax函数求导，直接等于A-Y，无需计算dA；

'''**********************************************************************'''
#单次后向运算
def single_backward(Y, dA, cache, mode, lambd):
    A_pre = cache['A_pre']
    W = cache['W']
    b = cache['b']
    A = cache['A']
    m = A_pre.shape[1]
    
    if mode=='softmax':             #根据本层激活函数计算本层的dZ
        dZ = (A-Y)                  #softmax函数 dL/dZ = AL-Y，不必再通过dL/dAL计算来计算dL/dZ
    if mode=='ReLU':
        dZ = dA                     #ReLU函数：A>=0,dZ=dA
        dZ[A<0] = 0
    if mode=='tanh':
        dZ = dA*(1-A**2)            #tanh函数: dZ=dA*(1-A*A) 
        
    #根据dZ, A_pre, W计算本层梯度dW db，同时计算dA_pre供前一层反向运算使用
    grad = {'dW':1.0/m*np.dot(dZ, A_pre.T) + lambd/m*W,
            'db':1.0/m*np.sum(dZ, axis=1, keepdims=True),
            'dA_pre':np.dot(W.T, dZ)}    
    return grad

后向传播函数中，最后一层也改为调用softmax函数，且该层dA=-Y/AL（这句代码在该程序中没用，因为计算dZ时没有用到dA）；

'''**********************************************************************'''    
#后向传播函数
def prop_backward(AL, Y, caches, lambd):
    grads = {}                      #注意：使用append时应初始化为[]，否则应为{}
    L = len(caches)
    
    for l in reversed(range(L)):    #计算梯度
        if l==L-1:                  #计算dAL
            dA = -Y/AL              #该步运算没有实际用途，因为softmax函数 dL/dZ = AL-Y，不必再计算dL/dAL
            mode = 'softmax'
        else:
            dA = grad['dA_pre']
            mode = 'tanh'
        grad = single_backward(Y, dA, caches[l], mode, lambd)
        grads['dW'+str(l+1)] = grad['dW']
        grads['db'+str(l+1)] = grad['db']
        
    return grads

预测函数，比较简单粗暴地用了np.round。

'''**********************************************************************'''
#预测函数
def predict(X,parameters,lambd):
    AL, caches, L2_SUM = prop_forward(X, parameters,lambd)
    prediction = np.round(AL)
    return prediction

同时还使用了L2正则化、minibatch、Adam。

试验效果

试验代码如下

X,Y,y = gendata()

x_min, x_max = X[0, :].min() - 1, X[0, :].max() + 1
y_min, y_max = X[1, :].min() - 1, X[1, :].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01),np.arange(y_min, y_max, 0.01)) #将二维平面以0.01*0.01的间隔散开，xx为每个点的横坐标，yy为每个点的纵坐标
zz = np.array([xx.ravel(), yy.ravel()]).T   #zz为每个点的横纵坐标，其行数为总点数，列数为特征数，即维度


layer_dims = [2,288,144,72,36,18,6,3]
steps = 100                         #训练次数
rate = 0.01                         #训练步长
print_flag = True                   #打印cost标识
lambd = 0                           #L2正则化系数，为0时不进行正则化
batch_size = 600                    #mini_batch_size，为1时即为随机梯度下降，为X.shape[1]时即不分批

parameters,costs = NN_model(X, Y, layer_dims, steps, rate, lambd, batch_size, print_flag)
plt.plot(costs)
prediction = predict(X,parameters,lambd)    #根据训练出来的神经网络，对X进行预测
p_NN = np.mean(prediction==Y)               #计算预测的准确率
print('\nL层神经网络的准确率为：%f'%p_NN)

Z_NN_predict = predict(zz.T,parameters,lambd)    #通过神经网络对每个点进行预测
Z_NN = np.zeros(Z_NN_predict.shape[1])
for i in range(Z_NN_predict.shape[1]):
    if Z_NN_predict[0,i]==1:
        Z_NN[i] = 0
    if Z_NN_predict[1,i]==1:
        Z_NN[i] = 1
    if Z_NN_predict[2,i]==1:
        Z_NN[i] = 2
        
Z_NN = Z_NN.reshape(xx.shape)
plt.figure(2)
plt.scatter(X[0, :], X[1, :], c=np.squeeze(y), s=10, cmap=plt.cm.Spectral)
plt.contourf(xx, yy, Z_NN, alpha=0.4,cmap=plt.cm.Spectral)     #绘制等高线
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.show()

试验效果如下：

​​​​​

Batchnorm

概念

批标准化（Batch Normalization，BN）和之前的数据集标准化类似，是将分散的数据进行统一的一种做法。具有统一规格的数据，能让机器更容易学习到数据中的规律。

对于一个神经网络，前面权重值的不断变化就会带来后面权重值的不断变化，批标准化减缓了隐藏层权重分布变化的程度。采用批标准化之后，尽管每一层的z还是在不断变化，但是它们的均值和方差将基本保持不变，这就使得后面的数据及数据分布更加稳定，减少了前面层与后面层的耦合，使得每一层不过多依赖前面的网络层，最终加快整个神经网络的训练。

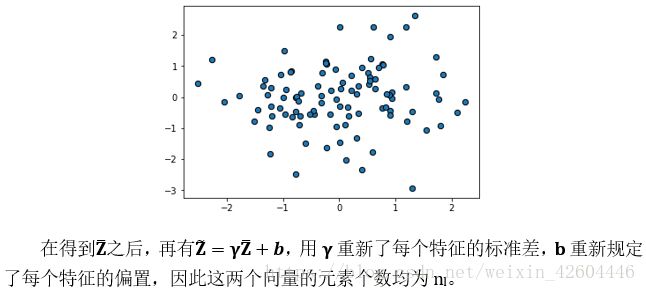
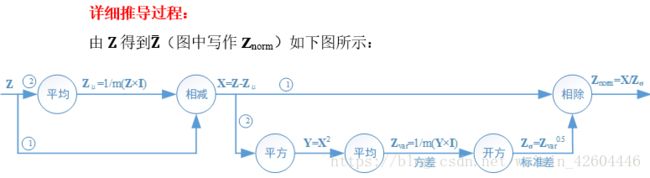
正向过程

(本来录入完了，csdn对 word的兼容实在太差……中间报了几次服务器错误，我也没理会，结果发现，辛辛苦苦改的博文木有了！！！哎，我还是直接从笔记里截图过来吧……）

反向过程

import numpy as np

np.random.seed(0)
Z = np.random.randn(2,100)              #2*100的矩阵Z，2个特征，100个样本
dZnorm = np.random.randn(2,100)*0.5     #2*100的矩阵dZnorm，2个特征，100个样本

nl = Z.shape[0]
m = Z.shape[1]

#方法1
mu = np.mean(Z,axis=1).reshape(nl,1)    #用np.mean直接计算平均值，2*1的矩阵
var = np.var(Z,axis=1).reshape(nl,1)    #用np.var直接计算方差，2*1的矩阵
sigma = np.sqrt(var)                    #方差开方得到标准差，2*1的矩阵
temp1 = dZnorm/sigma                    #用np.sum的方法计算dZ
temp2 = -1.0 / m / sigma * np.sum(dZnorm,axis=1).reshape(nl,1)
temp3 = -1.0 / m / (sigma**3) * (Z-mu) * np.sum(dZnorm*(Z-mu),axis=1).reshape(nl,1)
dZ_1 = temp1+temp2+temp3

#方法2
I = np.ones((m,m))
Z_mu = 1.0/m * np.dot(Z,I)              #用乘以全1矩阵的方法计算平均值，2*100的矩阵
Z_var = 1.0/m*np.dot((Z-Z_mu)**2,I)     #用乘以全1矩阵的方法计算方差，2*100的矩阵
Z_sigma = np.sqrt(Z_var)                #方差开方得到标准差，2*100的矩阵
temp4 = dZnorm/Z_sigma                  #用乘以全1矩阵的方法计算dZ
temp5 = -1.0 / m / Z_sigma * np.dot(dZnorm,I)
temp6 = -1.0 / m / (Z_sigma**3) * (Z-Z_mu) * np.dot(dZnorm*(Z-Z_mu),I)
dZ_2 = temp4+temp5+temp6

#比较
print(np.round(temp1-temp4))
print(np.round(temp2-temp5))
print(np.round(temp3-temp6))
print(np.round(dZ_1-dZ_2))

运行证明两者效果相同！

Batchnorm实现代码

在保留上面代码的基础上更改，代码更改如下：

初始化参数函数中增加标准差向量D，相应初始化adam函数以及更新参数中都要增加对应向量：

'''**********************************************************************'''
#初始化参数
def init_para(layer_dims):
    L = len(layer_dims)             #L为总层数
    np.random.seed(L)
    parameters = {}
    
    for l in range(1,L):            #初始化W1~WL,b1~bL
        n1 = layer_dims[l]
        n2 = layer_dims[l-1]
        if l==(L-1):                #最后一层用softmax函数，初始化时应为1/n2
            a = 1.0
        else:                       #其他层用ReLU函数，初始化时应为2/n2
            a = 2.0
        parameters['W'+str(l)] = np.random.randn(n1, n2) * np.sqrt(a/n2)
        parameters['D'+str(l)] = np.ones((n1, 1))
        parameters['b'+str(l)] = np.zeros((n1, 1))
        
    return parameters

单次前向函数（注意单个样本时，要特殊处理，原因可在调试时自行分析）：

'''**********************************************************************'''
#单次前向运算
def single_forward(A_pre, W, D, b, mode):
    epsilon = 1e-8
    Z = np.dot(W, A_pre)                #根据上一层的输出A_pre，以及本层的W b计算本层的Z
    if Z.shape[1] != 1:                 #表示不是再进行单个样本运算
        Z_mu = np.mean(Z, axis = 1).reshape(Z.shape[0],1) #reshape(Z.shape[0],1)或者keepdims=True都可以，目的是让其从向量变为矩阵（列数为1）
        Z_var = np.var(Z, axis = 1).reshape(Z.shape[0],1)+epsilon #epsilon防止Z_norm计算时除以0，在这里加，还方便了反向求导运算
        Z_norm = (Z - Z_mu)/(np.sqrt(Z_var))
    else:                               #表示在进行单个样本的运算
        Z_mu = 0                        #令平均值为0
        Z_var = 1                       #令方差为1
        Z_norm = Z                      #将Z直接赋给其标准化的值
    
    Z_bn = D * Z_norm + b
    
    if mode=='softmax':                 #根据所选定的激活函数计算本层的输出
        A = np.exp(Z_bn)/np.sum(np.exp(Z_bn),axis=0)
    if mode=='ReLU':
        A = (Z_bn+abs(Z_bn))/2
    if mode=='tanh':
        A = np.tanh(Z_bn)
        
    cache = {'A_pre':A_pre,
             'W':W,
             'D':D,
             'b':b,
             'Z':Z,
             'Z_mu':Z_mu,
             'Z_var':Z_var,
             'Z_norm':Z_norm,
             'Z_bn':Z_bn,
             'A':A}
    
    return cache

单次后向函数

'''**********************************************************************'''
#单次后向运算
def single_backward(Y, dA, cache, mode, lambd):
    A_pre = cache['A_pre']
    W = cache['W']
    D = cache['D']
    b = cache['b']
    A = cache['A']
    Z = cache['Z']
    Z_mu = cache['Z_mu']
    Z_var = cache['Z_var']
    Z_sigma = np.sqrt(Z_var)
    Z_norm = cache['Z_norm']
    m = A_pre.shape[1]
    
    if mode=='softmax':                #根据本层激活函数计算本层的dZ
        dZ_bn = (A-Y)                  #softmax函数 dL/dZ_bn = AL-Y，不必再通过dL/dAL计算来计算dL/dZ_bn
    if mode=='ReLU':
        dZ_bn = dA                     #ReLU函数：A>=0,dZ_bn=dA
        dZ_bn[A<0] = 0                 #ReLU函数：A<0, dZ_bn=0
    if mode=='tanh':
        dZ_bn = dA*(1-A**2)            #tanh函数: dZ_bn=dA*(1-A*A) 
    
    dD = 1.0/m*np.sum(dZ_bn*Z_norm, axis=1, keepdims=True)
    db = 1.0/m*np.sum(dZ_bn, axis=1, keepdims=True)
    dZ1 = D*dZ_bn/Z_sigma                    #用np.sum的方法计算dZ
    dZ2 = -1.0 / m / Z_sigma * np.sum(D*dZ_bn,axis=1, keepdims=True)
    dZ3 = -1.0 / m / (Z_sigma**3) * (Z-Z_mu) * np.sum(D*dZ_bn*(Z-Z_mu),axis=1, keepdims=True)
    dZ = dZ1 + dZ2 + dZ3
    dW = 1.0/m*np.dot(dZ, A_pre.T) + lambd/m*W
    dA_pre = np.dot(W.T, dZ)
    
    #根据dZ, A_pre, W计算本层梯度dW db，同时计算dA_pre供前一层反向运算使用
    grad = {'dW':dW,
            'dD':dD,
            'db':db,
            'dA_pre':dA_pre}    
    return grad

实施效果

读取课程的手势图形文件，建立神经网络，参数如下：

layer_dims = [X_train.shape[0],24,12,6]
steps = 200                         #训练次数
rate = 0.002                        #训练步长
print_flag = True                   #打印cost标识
lambd = 0.1                         #L2正则化系数，为0时不进行正则化
batch_size = 128                    #mini_batch_size，为1时即为随机梯度下降，为X.shape[1]时即不分批

对手势训练集和测试集的预测准确率分别为1，0.951。

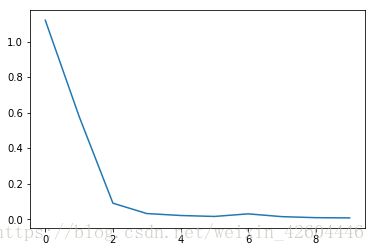
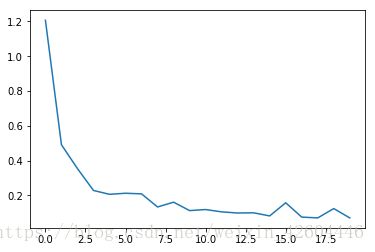
成本下降过程如下（每10次全样本训练记录一次成本）：

总结

推导过程中走了不少弯路，csdn上很多博客也说的不明不白，好在想到了batchnorm中的平均运算可以用矩阵乘法表示，后面的推导就豁然开朗。

后续还需要认真学习tensorflow，虽然用了tensorflow自带的softmax，但并没有用tensorflow自带的batchnorm。加油！！！

附

作业的源代码在我的资源中，可用spyder直接运行，感兴趣的朋友可以下载。