暴力递归到动态规划

动态规划就是暴力尝试减少重复计算的技巧

1)找到什么可变参数可以代表一个递归状态，也就是哪些参数一旦确定，返回值就确定了 
2)把可变参数的所有组合映射成一张表，有 1 个可变参数就是一维表，2 个可变参数就 是二维表，......
3)最终答案要的是表中的哪个位置，在表中标出 
4)根据递归过程的 base case，把这张表的最简单、不需要依赖其他位置的那些位置填好 值
5)根据递归过程非base case的部分，也就是分析表中的普遍位置需要怎么计算得到，那 么这张表的填写顺序也就确定了
6)填好表，返回最终答案在表中位置的值

暴力递归尝试(从左至右\范围)
->
转化成记忆搜索
->
转化成严格表结构的DP
->
观察表结构进行优化

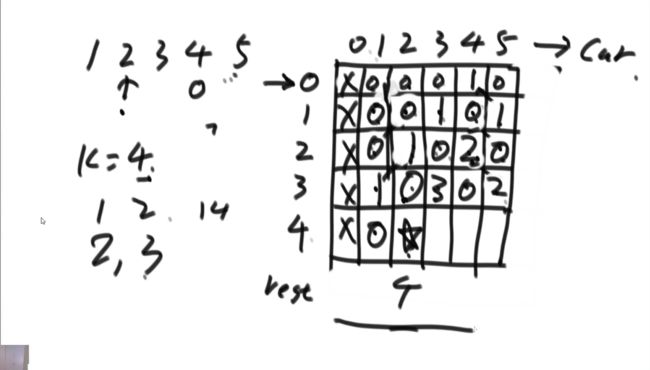
题目一：机器人达到指定位置方法数

题目：
假设有排成一行的 N 个位置，记为 1~N，N 一定大于或等于 2
开始时机器人在其中的 M 位 置上(M 一定是 1~N 中的一个)，机器人可以往左走或者往右走
如果机器人来到 1 位置， 那 么下一步只能往右来到 2 位置;如果机器人来到 N 位置，那么下一步只能往左来到 N-1 位置。
规定机器人必须走 K 步，最终能来到 P 位置(P 也一定是 1~N 中的一个)的方法有多少种
给 定四个参数 N、M、K、P，返回方法数
=============================================================================================
举例：
N=5,M=2,K=3,P=3 
上面的参数代表所有位置为 1 2 3 4 5。机器人最开始在 2 位置上，必须经过 3 步，最后到 达 3 位置。
走的方法只有如下 3 种: 
1)从2到1，从1到2，从2到3
2)从2到3，从3到2，从2到3 
3)从2到3，从3到4，从4到3 所以返回方法数 3。
N=3,M=1,K=3,P=3 
上面的参数代表所有位置为 1 2 3。
机器人最开始在 1 位置上，必须经过 3 步，最后到达 3 位置。怎么走也不可能，所以返回方法数 0。

package class08;

/**
 * @title: RobotWalk
 * @Descriptor: 总共N个位置，从M点出发，还剩K步，返回最终能到达P的方法数
 * @Author DD
 * @Date: 2022/6/8 11:01
 * @Version 1.0
 */

public class RobotWalk {

    public static int way1(int N, int M, int K, int P) {
        if (N < 2 || K < 1 || M < 1 || M > N || P < 1 || P > N) {
            return 0;
        }
        return walk(N, M, K, P);
    }

    public static int walk(int N, int cur, int rest, int P) {
        if (rest == 0) {
            return cur == P ? 1 : 0;
        }
        //  rest > 0 还可以继续走
        if (cur == 1) {
            return walk(N, cur + 1, rest - 1, P);
        }
        if (cur == N) {
            return walk(N, cur - 1, rest - 1, P);
        }
        return walk(N, cur + 1, rest - 1, P) + walk(N, cur - 1, rest - 1, P);
    }

    public static int way2(int N, int M, int K, int P) {
        //  记忆搜索

        if (N < 2 || K < 1 || M < 1 || M > N || P < 1 || P > N) {
            return 0;
        }
        int[][] dp = new int[K + 1][N + 1];
        for (int i = 0; i <= K; i++) {
            for (int j = 0; j <= N; j++) {
                dp[i][j] = -1;
            }
        }
        return walk2(N, M, K, P, dp);
    }

    public static int walk2(int N, int cur, int rest, int P, int[][] dp) {

        if (dp[rest][cur] != -1) {//  当前状态之前已经计算过
            return dp[rest][cur];
        }
        //  之前没计算过该状态
        if (rest == 0) {
            dp[rest][cur] = cur == P ? 1 : 0;
            return dp[rest][cur];
        }
        //  rest > 0 还可以继续走
        if (cur == 1) {
            dp[rest][cur] = walk(N, cur + 1, rest - 1, P);
            return dp[rest][cur];
        } else if (cur == N) {
            dp[rest][cur] = walk(N, cur - 1, rest - 1, P);
            return dp[rest][cur];
        } else {
            dp[rest][cur] = walk(N, cur + 1, rest - 1, P) + walk(N, cur - 1, rest - 1, P);
        }
        return dp[rest][cur];
    }

    public static int way3(int N, int M, int K, int P) {
        //  严格表结构的动态规划
        if (N < 2 || K < 1 || M < 1 || M > N || P < 1 || P > N) {
            return 0;
        }
        int[][] dp = new int[K + 1][N + 1];
        return walk3(N,M,K,P,dp);
    }

    public static int walk3(int N,int cur,int rest,int P,int[][] dp){

        // 参数无效直接返回0
        if (N < 2 || rest < 1 || cur < 1 || cur> N || P < 1 || P > N) {
            return 0;
        }
        dp[0][P] = 1;
        for (int i = 1; i <= rest; i++) {
            for (int j = 1; j <= N; j++) {
                if (j == 1) {
                    dp[i][j] = dp[i - 1][2];
                } else if (j == N) {
                    dp[i][j] = dp[i - 1][N - 1];
                } else {
                    dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j + 1];
                }
            }
        }
        return dp[rest][cur];
    }

    public static int way4(int N, int M, int K, int P) {
        //  严格表结构的动态规划 -- 省空间版
        if (N < 2 || K < 1 || M < 1 || M > N || P < 1 || P > N) {
            return 0;
        }
        return walk4(N, M, K, P);
    }

    public static int walk4(int N, int M, int K, int P) {

        // 参数无效直接返回0
        if (N < 2 || K < 1 || M < 1 || M > N || P < 1 || P > N) {
            return 0;
        }
        int[] dp = new int[N + 1];
        dp[P] = 1;
        for (int i = 1; i <= K; i++) {
            int leftUp = dp[1];// 左上角的值
            for (int j = 1; j <= N; j++) {
                int tmp = dp[j];
                if (j == 1) {
                    dp[j] = dp[j + 1];
                } else if (j == N) {
                    dp[j] = leftUp;
                } else {
                    dp[j] = leftUp + dp[j + 1];
                }
                leftUp = tmp;
            }
        }
        return dp[M];
    }

    public static void main(String[] args) {
        System.out.println(way2(5, 2, 4, 4));
        System.out.println(way3(5,2,4,4));
        System.out.println(way4(5, 2, 4, 4));
    }
}

题目二：换钱的最少货币数

【题目】 
给定数组 arr，arr 中所有的值都为正数且不重复。
每个值代表一种面值的货币，每种面值 的货币可以使用任意张，
再给定一个整数 aim，代表要找的钱数，求组成 aim 的最少货币数。
【举例】
arr=[5,2,3]，aim=20  4张5元可以组成 20 元，其他的找钱方案都要使用更多张的货币，所以返回4。 
arr=[5,2,3]，aim=0   不用任何货币就可以组成 0 元，返回 0。
arr=[3,5]，aim=2     根本无法组成 2 元，钱不能找开的情况下默认返回-1

package class08;

/**
 * @title: minCoins
 * @Descriptor: 换钱的最少货币数
 * @Author DD
 * @Date: 2022/6/19 16:42
 * @Version 1.0
 */

public class minCoins {

    //  暴力递归版本

    public static int minCoins1(int[] arr, int aim) {
        if (aim == 0) {
            return 0;
        }
        return process1(arr, 0, aim);
    }

    public static int process1(int[] arr, int i, int rest) {
        // 从arr[i....] 中组出rest这么多钱,所用的最少货币数
        if (rest < 0) {
            //  之前的组合导致钱数大于aim 失败
            return -1;
        }
        if (rest == 0) {
            //  之前的组合刚好凑出了aim 无需使用之后的货币了
            return 0;
        }
        //  rest>0
        if (i == arr.length) {
            //  之前的组合把钱用完了 没有可供凑数的
            return -1;
        }
        //  rest>0 并且 还有可供凑数的钱
        int p1 = process1(arr, i + 1, rest); // 没有选择i位置上的钱
        int p2Next = process1(arr, i + 1, rest - arr[i]); // 选了i位置上的钱
        if (p1 == -1 && p2Next == -1) { //   选不选都不能满足要求
            return -1;
        } else {
            if (p1 == -1) {
                return p2Next + 1;
            }
            if (p2Next == -1) {
                return p1;
            }
            return Math.min(p1, p2Next + 1);
        }
    }

    public static int minCoins2(int[] arr, int aim) {
        //  记忆搜索版本
        if (aim == 0) {
            return 0;
        }
        int[][] dp = new int[arr.length + 1][aim + 1];
        for (int i = 0; i < arr.length + 1; i++) {
            for (int j = 0; j < aim + 1; j++) {
                dp[i][j] = -2;  //  初始化记忆数组 -2表示未访问过
            }

        }
        return process2(arr, 0, aim, dp);
    }

    public static int process2(int[] arr, int i, int rest, int[][] dp) {

        if (rest < 0) {
            //  之前的组合导致钱数大于aim 失败
            return -1;
        }
        if (rest == 0) {
            //  之前的组合刚好凑出了aim 无需使用之后的货币了
            dp[i][rest] = 0;
        } else if (i == arr.length) {//  rest>0
            //  之前的组合把钱用完了 没有可供凑数的
            dp[i][rest] = -1;
        } else {
            //  rest>0 并且 还有可供凑数的钱
            int p1 = process1(arr, i + 1, rest); // 没有选择i位置上的钱
            int p2Next = process1(arr, i + 1, rest - arr[i]); // 选了i位置上的钱
            if (p1 == -1 && p2Next == -1) { //   选不选都不能满足要求
                dp[i][rest] = -1;
            } else {
                if (p1 == -1) {
                    dp[i][rest] = p2Next + 1;
                } else if (p2Next == -1) {
                    dp[i][rest] = p1;
                } else {
                    dp[i][rest] = Math.min(p2Next + 1, p1);
                }
            }
        }
        return dp[i][rest];
    }

    public static int minCoins3(int[] arr, int aim) {

        //  严格表结构的动态规划

        int N = arr.length;
        int[][] dp = new int[N + 1][aim + 1];

        for (int col = 1; col < aim + 1; col++) {
            dp[N][col] = -1;
        }

//        for (int i = 0; i < N + 1; i++) {
//            for (int j = 0; j < aim + 1; j++) {
//                System.out.print(dp[i][j]);
//                if (j == aim) {
//                    System.out.println();
//                }
//            }
//        }
//        System.out.println("=============");

        for (int i = N - 1; i >= 0; i--) {
            for (int rest = 1; rest <= aim; rest++) {

                //  rest>0 并且 还有可供凑数的钱
//                int p1 = process1(arr, i + 1, rest); // 没有选择i位置上的钱
                int p1 = dp[i + 1][rest];
//                int p2Next = process1(arr, i + 1, rest - arr[i]); // 选了i位置上的钱
                int p2Next = -1;
                if (rest - arr[i] >= 0) {
                    p2Next = dp[i + 1][rest - arr[i]];
                }

                if (p1 == -1 && p2Next == -1) { //   选不选都不能满足要求
                    dp[i][rest] = -1;
                } else {
                    if (p1 == -1) {
                        dp[i][rest] = p2Next + 1;
                    } else if (p2Next == -1) {
                        dp[i][rest] = p1;
                    } else {
                        dp[i][rest] = Math.min(p1, p2Next + 1);
                    }
                }
            }
        }
//        for (int i = 0; i < N + 1; i++) {
//            for (int j = 0; j < aim + 1; j++) {
//                System.out.print(dp[i][j]);
//                if (j == aim) {
//                    System.out.println();
//                }
//            }
//        }
        return dp[0][aim];

    }

    public static void main(String[] args) {
        int[] money = {2, 3, 5, 7, 2};
        System.out.println(minCoins1(money, 2));
        System.out.println(minCoins1(money, 5));
        System.out.println(minCoins1(money, 150));
        System.out.println(minCoins1(money, 10));
        System.out.println("=======================");
        System.out.println(minCoins2(money, 2));
        System.out.println(minCoins2(money, 5));
        System.out.println(minCoins2(money, 150));
        System.out.println(minCoins2(money, 10));
        System.out.println("=======================");
//        minCoins3(money, 10);
        System.out.println(minCoins3(money, 2));
        System.out.println(minCoins3(money, 5));
        System.out.println(minCoins3(money, 150));
        System.out.println(minCoins3(money, 10));
    }
}

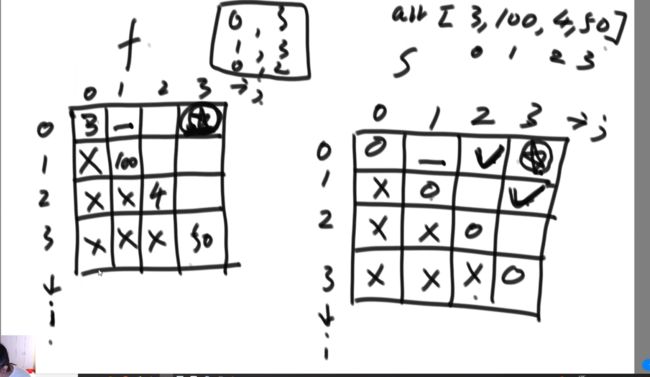
题目三：排成一条线的纸牌博弈问题

给定一个整型数组arr，代表数值不同的纸牌排成一条线。玩家A和玩家B依次拿走每张纸牌，
规定玩家A先拿，玩家B后拿，但是每个玩家每次只能拿走最左或最右的纸牌，
玩家A 和玩家B都绝顶聪明。请返回最后获胜者的分数。 
【举例】
arr=[1,2,100,4]
开始时，玩家A只能拿走1或4。如果开始时玩家A拿走1，则排列变为[2,100,4]，
接下来 玩家 B可以拿走2或4，然后继续轮到玩家A... 
如果开始时玩家A拿走4，则排列变为[1,2,100]，接下来玩家B可以拿走1或100，然后继续轮到玩家A... 
玩家A作为绝顶聪明的人不会先拿4，因为拿4之后，玩家B将拿走100。
所以玩家A会先拿1,让排列变为[2,100,4]，接下来玩家B不管怎么选，100都会被玩家 A拿走。	玩家A会获胜,
分数为101。所以返回101.

package class08;

/**
 * @title: cardInLine
 * @Descriptor: 给定一个整型数组arr，代表数值不同的纸牌排成一条线。玩家A和玩家B依次拿走每张纸牌，
 *              规定玩家A先拿，玩家B后拿，但是每个玩家每次只能拿走最左或最右的纸牌，玩家A和玩家B都绝顶聪明。请返回最后获胜者的分数。
 * @Author DD
 * @Date: 2022/5/30 17:07
 * @Version 1.0
 */

public class cardInLine {

    public static int win1(int[] arr) {
        if (arr == null || arr.length == 0) {
            return 0;
        }
        return Math.max(f(arr, 0, arr.length - 1), s(arr, 0, arr.length - 1));
    }

    //  先手 在arr的i~j范围内所能得到的最大分数
    public static int f(int[] arr, int i, int j) {
        if (i == j) {   //  牌组中仅剩一张牌
            return arr[i];  //  因为是先手 所以能得到这张牌
        }
        //  牌组中至少余两张
        //  从左右两端选择一张后,对于剩余的牌组来说 肯定是别人先取一张 之后轮到自己 ==> 成为新牌组的后手
        //  (当前所选牌+后手时所能拿到的最大分数) ==> 即为最终最终总分
        //  返回最终总分大的
        return Math.max(arr[i] + s(arr, i + 1, j), arr[j] + s(arr, i, j - 1));
    }

    //  后手 在arr的i~j范围内所能得到的最大分数
    public static int s(int[] arr, int i, int j) {
        if (i == j) {   //  牌组中仅剩一张牌
            return 0;   //  因为是后手 所以得不到这张牌
        }
        int p1 = f(arr, i + 1, j);  //  对手选了arr[i]后最终所能达到的最大分数
        int p2 = f(arr, i, j - 1);  //  对手选了arr[j]后最终所能达到的最大分数
        //  让对手所得到的分数尽可能的小
        return Math.min(p1, p2);
    }

    public static int win2(int[] arr) {

        //  范围递归转DP 先画图

        if (arr == null || arr.length == 0) {
            return 0;
        }
        int[][] f = new int[arr.length][arr.length];
        int[][] s = new int[arr.length][arr.length];
        for (int j = 0; j < arr.length; j++) {
            f[j][j] = arr[j];
            for (int i = j - 1; i >= 0; i--) {
                f[i][j] = Math.max(arr[i] + s[i + 1][j], arr[j] + s[i][j - 1]);
                s[i][j] = Math.min(f[i + 1][j], f[i][j - 1]);
            }
        }
        return Math.max(f[0][arr.length - 1], s[0][arr.length - 1]);
    }

    public static void main(String[] args) {
        int[] arr = {1, 9, 1};
        System.out.println(win1(arr));
        System.out.println(win2(arr));
//        System.out.println(win3(arr));
    }
}

题目四：想起中马的跳法(三维尝试改DP)

【题目】 
请同学们自行搜索或者想象一个象棋的棋盘，然后把整个棋盘放入第一象限，棋盘的最左下 角是(0,0)位置。
那么整个棋盘就是横坐标上9条线、纵坐标上10条线的一个区域。
给你三个 参数，x，y，k，
返回如果“马”从(0,0)位置出发，必须走k步，最后落在(x,y)上的方法数有多少种

要第Step步跳到目标位置,只需找(Step-1)步跳到目标周围(下一步跳一下就可以到目标)
抽象成三维表结构

package class08;

/**
 * @title: horseJump
 * @Descriptor: 象棋中马的跳法
 * @Author DD
 * @Date: 2022/6/20 14:57
 * @Version 1.0
 */

public class horseJump {
    public static int getWays(int x, int y, int step) {
        return process(x, y, step);
    }

    public static int process(int x, int y, int step) {
        if (x < 0 || x > 8 || y < 0 || y > 9) {
            return 0;
        }
        if (step == 0) {
            return (x == 0 && y == 0) ? 1 : 0;
        }
        return process(x - 1, y + 2, step - 1)
                + process(x + 1, y + 2, step - 1)
                + process(x + 2, y + 1, step - 1)
                + process(x + 2, y - 1, step - 1)
                + process(x + 1, y - 2, step - 1)
                + process(x - 1, y - 2, step - 1)
                + process(x - 2, y - 1, step - 1)
                + process(x - 2, y + 1, step - 1);
    }

    public static int dpWays(int x, int y, int step) {
        if (x < 0 || x > 8 || y < 0 || y > 9 || step < 0) {
            return 0;
        }
        int[][][] dp = new int[9][10][step + 1];
        dp[0][0][0] = 1;
        for (int h = 1; h <= step; h++) {
            for (int r = 0; r < 9; r++) {
                for (int c = 0; c < 10; c++) {
                    dp[r][c][h] += getValue(dp, r - 1, c + 2, h - 1);
                    dp[r][c][h] += getValue(dp, r + 1, c + 2, h - 1);
                    dp[r][c][h] += getValue(dp, r + 2, c + 1, h - 1);
                    dp[r][c][h] += getValue(dp, r + 2, c - 1, h - 1);
                    dp[r][c][h] += getValue(dp, r + 1, c - 2, h - 1);
                    dp[r][c][h] += getValue(dp, r - 1, c - 2, h - 1);
                    dp[r][c][h] += getValue(dp, r - 2, c - 1, h - 1);
                    dp[r][c][h] += getValue(dp, r - 2, c + 1, h - 1);
                }
            }
        }
        return dp[x][y][step];
    }

    public static int getValue(int[][][] dp, int row, int col, int step) {
        if (row < 0 || row > 8 || col < 0 || col > 9) {
            return 0;
        }
        return dp[row][col][step];
    }

    public static void main(String[] args) {
        int x = 7;
        int y = 7;
        int step = 10;
        System.out.println(getWays(x, y, step));
        System.out.println(dpWays(x, y, step));
    }
}

题目五:可重复使用面值凑目标钱数

【题目】 
arr内都是正数,没有重复值,每一个值代表一种面额的货币,每一种都可以重复使用
最终要找零钱数是aim
返回不同组合的方法数
==================================
[举例]
arr = [2,3,5] 希望凑成10元
case1: 2,2,2,2,2
case2: 2,3,5
case3: 2,2,3,3
case4: 5,5

package class08;

/**
 * @title: coinsWays
 * @Descriptor: 使用数组中提供的面值(可以重复使用)组合成目标面值 返回组合数
 * @Author DD
 * @Date: 2022/6/20 18:56
 * @Version 1.0
 */

public class coinsWays {

    //  arr内都是正数,没有重复值,每一个值代表一种面额的货币,每一种都可以重复使用
    //  最终要找零钱数是aim
    //  返回不同组合的方法数

    public static int way1(int[] arr, int aim) {
        return process(arr, 0, aim);
    }

    //  使用arr[index...]中的所有面值,凑成rest,返回所有凑法 -- 暴力递归
    public static int process(int[] arr, int index, int rest) {
        if (index == arr.length) {  // 所有面值都已尝试结束
            return rest == 0 ? 1 : 0;
        }
        //  使用 x张 arr[index]面值的货币 需要x*arr[index] 不越界
        int ways = 0;
        for (int zhang = 0; zhang * arr[index] <= rest; zhang++) {
            ways += process(arr, index + 1, rest - zhang * arr[index]);
        }
        return ways;
    }

    //  记忆搜索
    public static int way2(int[] arr, int aim) {
        int N = arr.length;
        int[][] dp = new int[N + 1][aim + 1];
        return process2(arr, 0, aim, dp);
    }

    private static int process2(int[] arr, int index, int rest, int[][] dp) {
        if (index == arr.length) {
            dp[index][rest] = rest == 0 ? 1 : 0;
            return dp[index][rest];
        }
        int ways = 0;
        for (int zhang = 0; zhang * arr[index] <= rest; zhang++) {
            ways += process2(arr, index + 1, rest - zhang * arr[index], dp);
        }
        dp[index][rest] = ways;
        return dp[index][rest];
    }

    //  严格表结构的动态规划
    public static int way3(int[] arr, int aim) {
        return process3(arr, 0, aim);
    }

    public static int process3(int[] arr, int index, int aim) {
        int N = arr.length;
        int[][] dp = new int[N + 1][aim + 1];
        dp[N][0] = 1;
        for (int i = N - 1; i >= 0; i--) {
            for (int j = 0; j <= aim; j++) {
                int ways = 0;
                for (int zhang = 0; zhang * arr[index] <= aim; zhang++) {
                    ways += process2(arr, index + 1, aim - zhang * arr[index], dp);
                }
                dp[i][j] = ways;
            }
        }
        return dp[0][aim];
    }

    //  表结构的优化
    //  当前数据依赖 arr[index+1][rest] 和 arr[index][rest - arr[index]](优化的点就在于避免了重复计算该项)
    public static int way4(int[] arr, int aim) {
        int N = arr.length;
        int[][] dp = new int[N + 1][aim + 1];
        dp[N][0] = 1;
        for (int i = N - 1; i >= 0; i--) {
            for (int j = 0; j <= aim; j++) {
                dp[i][j] = dp[i + 1][j];
                if (j - arr[i] >= 0) {
                    dp[i][j] += dp[i][j - arr[i]];
                }
            }
        }
        return dp[0][aim];
    }

    public static void main(String[] args) {
        int[] money = {2, 3, 5};
//        System.out.println(way1(money, 1));
        System.out.println(way3(money, 10));
        System.out.println(way3(money, 2));
        System.out.println(way4(money, 10));
        System.out.println(way4(money, 2));

    }
}