换钱的方法数
给定数组arr,arr中所有的值都为正整数且不重复。每个值代表一种面值的货币,每种面值的货币可以使用任意张,再给定一个整数aim代表要找的钱数,求换钱的方式数。
一、暴力递归
public static int coins1(int[] arr, int aim){
// 排除极端条件
if (arr == null || arr.length == 0 || aim < 0){
return 0;
}
return process1(arr, 0, aim);
}
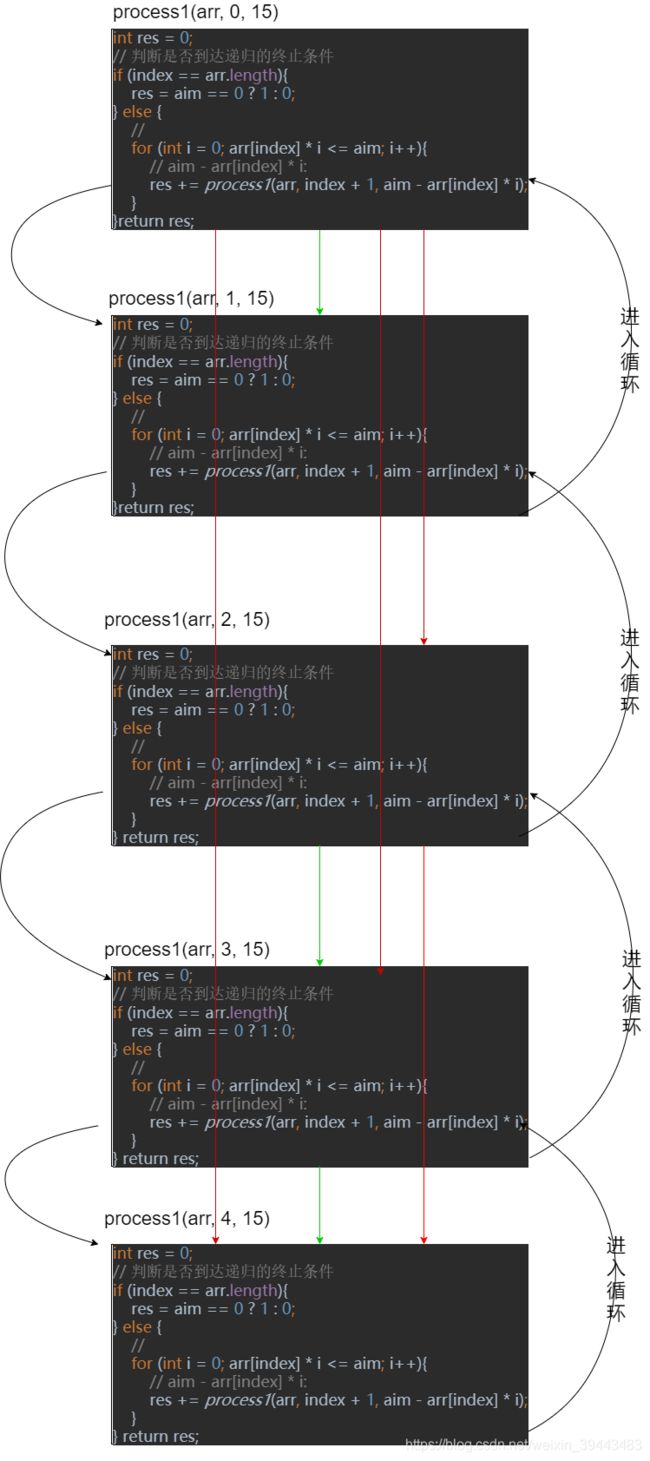
public static int process1(int[] arr, int index, int aim){
int res = 0;
// 判断是否到达递归的终止条件
if (index == arr.length){
res = aim == 0 ? 1 : 0;
} else {
//
for (int i = 0; arr[index] * i <= aim; i++){
//index:当前需要去拼凑的钱 aim - arr[index] * i:剩下的钱
res += process1(arr, index + 1, aim - arr[index] * i);
}
}
return res;
}二、暴力优化1
在暴力搜索方法的函数中看看哪些参数可以代表递归过程。
暴力递归都会存在大量的重复计算,是因为每一个递归过程的结果都没被记下来,所以下次还会重复计算,所以可以准备一个map,每计算完一个递归过程,都将结果记录到map中,当下次进行同样的递归过程之前,先在map中查询这个递归过程是否已经计算过,如果已经计算过,就直接拿出来用,如果没有计算过,需要再进入递归过程。记忆化搜索的方法是针对暴力递归最初级的优化,分析递归函数的状态可以由那些变量表示,做出相应的维度和大小的map即可,时间复杂度为O(N*am^2)。
public static int coins2(int[] arr, int aim){
if (arr == null || arr.length == 0 || aim < 0){
return 0;
}
// 暴力递归会产生大量的重复,是因为每个递归都被记录下来了,所以还要去重
// 可以通过一个map来表示p(index, aim)--p[index][aim]如果为重复计算的则不必重复去求了。
int[][] map = new int[arr.length + 1][aim + 1];
return process2(arr, 0, aim, map);
}
public static int process2(int[] arr, int index, int aim, int[][] map){
int res = 0;
if (index == arr.length){
res = aim == 0 ? 1 : 0;
} else {
int mapValue = 0;
for (int i = 0; arr[index] * i <= aim; i++){
mapValue = map[index + 1][aim - arr[index] * i];
if (mapValue != 0){
res += mapValue == -1 ? 0 : mapValue;
} else {
res += process2(arr, index + 1, aim - arr[index] * i, map);
}
}
}
map[index][aim] = res == 0 ? -1 : res;
return res;
}三、记忆搜索
记忆化搜索的方法是针对暴力递归最初级的优化技巧,分析递归函数的状态可以由哪些变量表示,做出相应纬度和大小的map即可。记忆化搜索方法的时间复杂度为O(N X aim^2).
动态规范方法。生成行数为N、列数为aim + 1的矩阵dp,dp[i][j]的含义是在使用arr[0...i]货币的情况下,组成钱数为j有多少种方法。dp[i][j]的值求法如下:
1. 对于矩阵dp第一列值dp[..][0],表示组成钱数为0的方法数,很明显是一种,也就是不使用任何货币。所以dp第一列的值统一设置为1.
2. 对于矩阵dp第一行的值dp[0][..],表示只能使用arr[0]这一种货币的情况下,组成钱数的方法,比如arr[0] = 5,能组成的钱数只有0, 5, 10, 15, ...。所以,令dp[0][k*arr[0]] = 1(0 <=k*arr[0]<=aim, k为非负整数).
3.除第1行和第一列的其它位置,记为位置(i,j)。dp[i][j]的值时以下几个值的累加。
- 完全不用arr[i]货币,只使用arr[0...i-1]货币时,方法数为dp[i-1][j].
- 用1张arr[i]货币,剩下的钱用arr[0...i-1]货币组成时,方法数为dp[i-1][j-arr[i]]。
- 用2张arr[i]货币,剩下的钱用arr[0...i-1]货币组成,方法数为dp[i-1][j-2*2*arr[i]].
- 。。。
- 用k张arr[i]货币,剩下的钱用arr[0...i-1]货币组成时,方法数为dp[i-1][j-k*arr[i]].
4. 最终dp[N-1][aim]的值就是最终结果。
public int coins3(int[] arr, int aim){
if (arr == null || arr.length == 0|| aim < 0){
return 0;
}
int [][] dp = new int[arr.length][aim + 1];
for (int i = 0; i < arr.length; i ++){
dp[i][0] = 1; //对于所有的钞票而言组成0元的方式都只有1种
}
for (int j = 1; arr[0] * j <= aim ; j ++){
dp[0][arr[0] * j] = 1; // 第一张纸币组成任何这个纸币的倍数的目标的方法都只有一种
}
int num = 0;
for (int i = 1; i < arr.lenght; i ++){
for (int j = 1; j <= aim; j ++){
num = 0;
// 转移方程dp[i][j] = dp[i-1][j - k*arr[i]]
for (int k = 0; j - arr[i] * k >= 0; k ++){
num += dp[i - 1][j - arr[i] * k];
}
dp[i][j] = num;
}
}
return dp[arr.length - 1][aim];
}
四、动态规划O(N * aim)
public int coins4(int[] arr, int aim){
if (arr == null || arr.length == 0 || aim < 0){
return 0;
}
int[][] dp = new dp[arr.length][aim + 1];
for (int i = 0; i < arr.length; i ++){
dp[i][0] = 1;
}
for (int j = 1; arr[0] * j < aim; j ++){
dp[0][arr[0] * j] = 1;
}
for (int i = 1; i < arr.length; i ++){
for (int j = 1; j < aim ; j++){
dp[i][j] = dp[i - 1][j];
dp[i][j] += j - arr[i] >= 0 ? dp[i][j - arr[i]] : 0;
}
}
return dp[arr.lenght -1 ][aim];
}时间复杂度为O(N * aim) 的动态规划方法再结合空间压缩的技巧。
public int coins5(int[] arr, int aim){
if (arr == null ||arr.length == 0 || aim < 0){
return 0;
}
int [] dp = new int[aim + 1] ;
for (int i = 1; i < arr.length; i ++){
for (int j = 1; i <= aim; j ++){
dp[j] += j - arr[i] >= 0 ? dp[j - arr[i]] : 0;
}
}
return dp[aim];
}