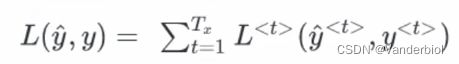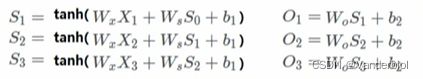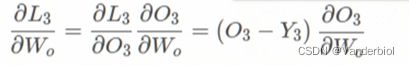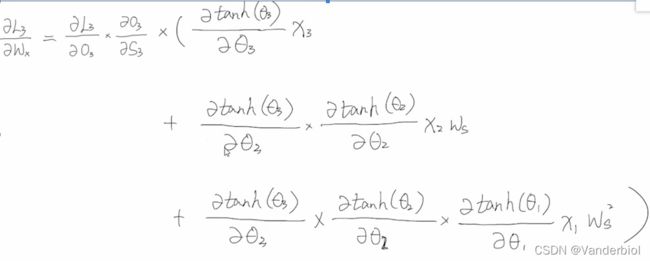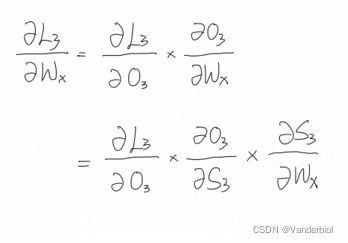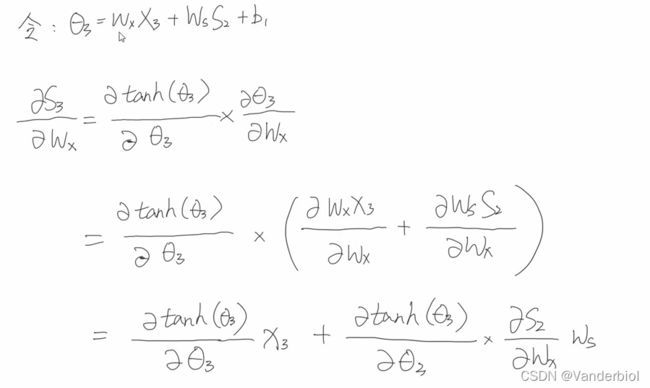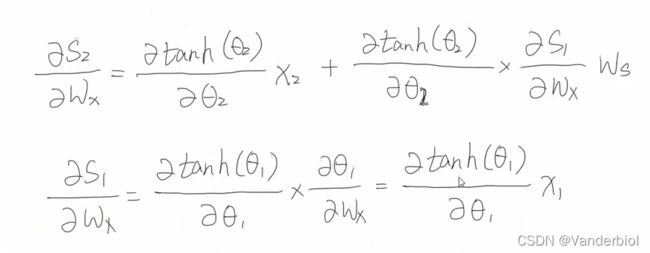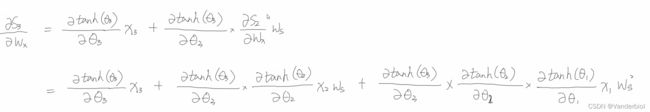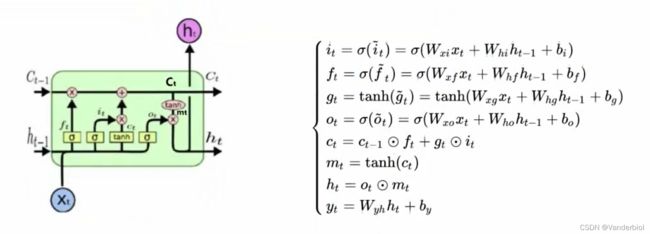深度学习与智能故障诊断学习笔记(三)——RNN与LSTM推导详解
1.RNN
1.1网络结构
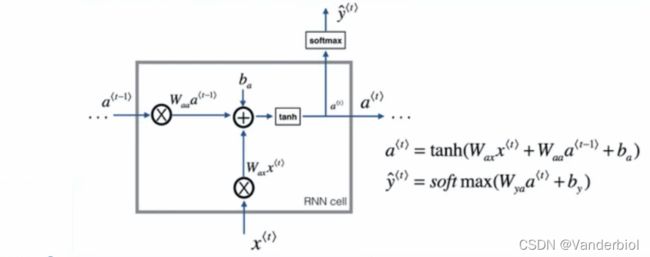
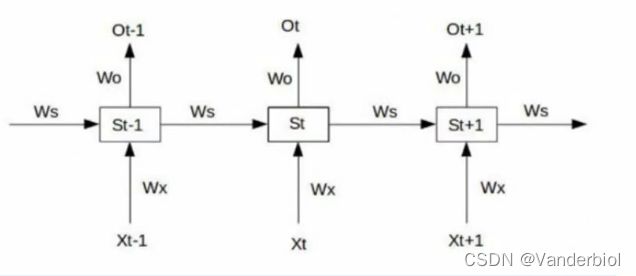
标准神经网络的输入输出在不同例子中可能有不同的长度,在学习中并不共享从不同位置上学到的特征。因为标准神经网络的训练集是稳定的,即所有的特征域表达的内容是同一性质的,一旦交换位置,就需要重新学习。故障诊断和健康管理属于带有时间序列的任务场景,在进行学习时参数量巨大,标准神经网络无法体现出时序上的前因后果,所以引入循环神经网络。如图所示为RNN循环神经网络的单元。
其中![]() 为当前输入,
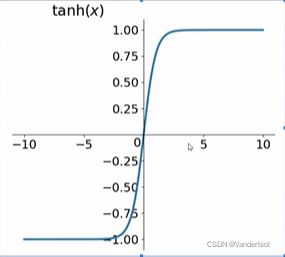
为当前输入,![]() 为前一个状态,b为偏置项,tanh为激活函数,用于学习非线性部分。当前输入和前一个状态分别乘以对应权重并相加,在加上偏置项,乘激活函数得到当前状态
为前一个状态,b为偏置项,tanh为激活函数,用于学习非线性部分。当前输入和前一个状态分别乘以对应权重并相加,在加上偏置项,乘激活函数得到当前状态![]() ,此状态在下一个神经元学习时又作为
,此状态在下一个神经元学习时又作为![]() 进行运算,由此实现时序关联。输出
进行运算,由此实现时序关联。输出![]() 的激活函数根据任务类型来选择,若是多分类可以选择softmax,若二分类则可直接选择sigmod。
的激活函数根据任务类型来选择,若是多分类可以选择softmax,若二分类则可直接选择sigmod。
(注:输出并非每个神经元都必须有,RNN可以是多输入多输出,也可以是多输入单输出,仅在学习完成后输出)
1.2RNN网络特点
RNN网络为串联结构,可以体现出“前因后果”,后面结果的生成要参考前面的信息,且所有特征共享一套参数。这使得RNN在面对不同的输入(两个方面),可以学习到不同的相应结果,并极大的减少了训练参数量。
(RNN输入和输出数据在不同场景中可以有不同的长度)
1.3损失函数
单个时间步的损失函数可根据多分类和二分类进行自定义
整个序列的损失函数是将所有单步损失函数相加,如式。
1.4传播过程
前向传播如图一所示。
反向传播
(图源自吴恩达老师课件)
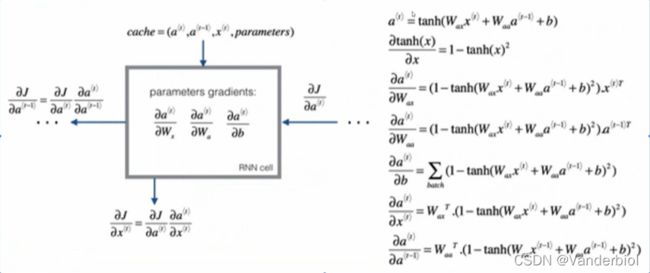
求解梯度即复合函数求导,按照链式法则进行求导。
反向传播具体过程需要按照损失函数来具体求解,但上式对所有RNN模型都适用。
1.5缺点
当序列太长时,容易产生梯度消失,参数更新只能捕捉到局部以来关系,没法再捕捉序列之间长期的关联或依赖关系。
如图为RNN连接,输入x,输出o(简单线性输出),权重w,s为生成状态。
根据前向传播可得:
假设使用平方误差作为损失函数,对单个时间点进行求梯度,假设再t=3时刻,损失函数为L3 = ![]() 。然后根据网络参数Wx,Ws,Wo,b1,b2等求梯度。
。然后根据网络参数Wx,Ws,Wo,b1,b2等求梯度。
Wo:
Wx(具体求解过程在下边):
经整理可得:
具体求解过程:
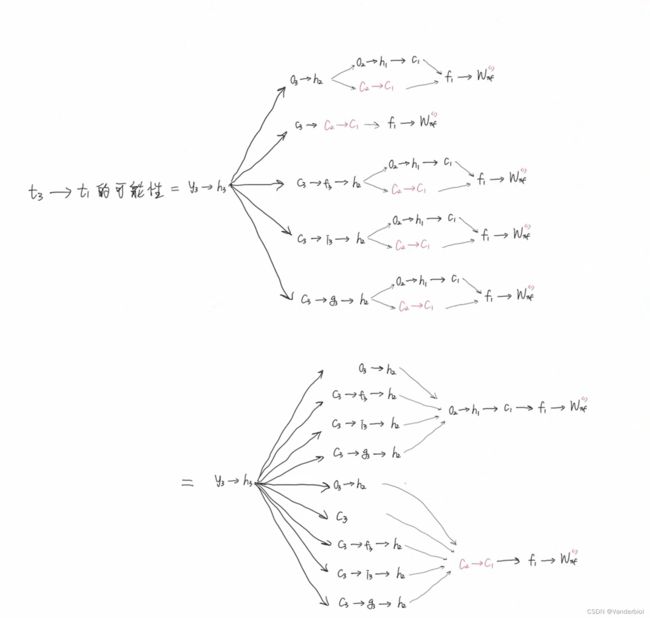
首先,所求目标为L3对Wx的偏导,通过链式法则进行展开。对比前向传播公式图可知,O3中并不能直接对Wx求偏导,而是包含在S3中,所以要展开成如下形式。
但在S3中又包含S2,S2中包含Wx和S1,S1中又包含Wx,嵌套了很多层,为了方便表示,我们用![]() 3来表示S3括号中的内容。进一步简化可得:
3来表示S3括号中的内容。进一步简化可得:
由该式可以看出,梯度的更新同时依赖于x3,x2,x1包括其梯度值。将该式处理为
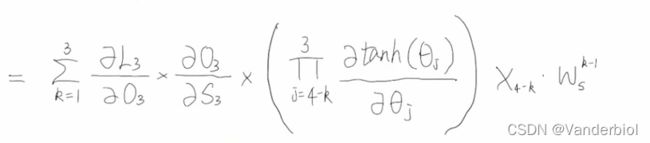
此为t=3时刻的梯度公式,推广至任意时刻的梯度公式为:
此式括号中的项为求导的连乘,此处求出的导数是介于0-1之间的,有一定的机率导致梯度消失(但非主要原因)。造成梯度消失和梯度爆炸的主要原因是最后一项:当Ws很小的时候,它的k-1的次方会无限接近于0,而当Ws大于1时,它的k-1次方会很大。
如下为t=20时梯度更新计算的结果:
从式中可以看出,t=3的节点由于连乘过多导致梯度消失,无法将信息传给t=20,因此t=20的更新无法引入t=3时的信息,认为t=20节点跟t=3的节点无关联。
对于梯度爆炸和梯度消失,可以通过梯度修剪来解决。相对于梯度爆炸,梯度消失更难解决。而LSTM很好的解决了这些问题。
2.LSTM
2.1设计思路
RNN是想把所有信息都记住,不管是有用的信息还是没用的信息。而LSTM设计了一个记忆细胞,具备选择性记忆功能,可以选择记忆重要信息,过滤掉噪声信息,减轻记忆负担。
2.2整体结构
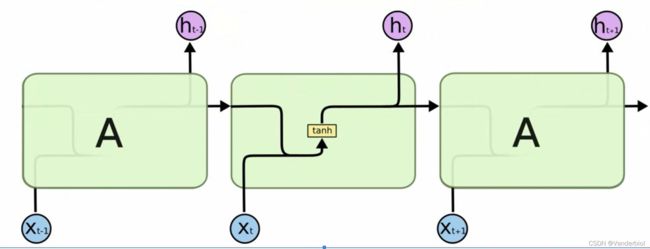
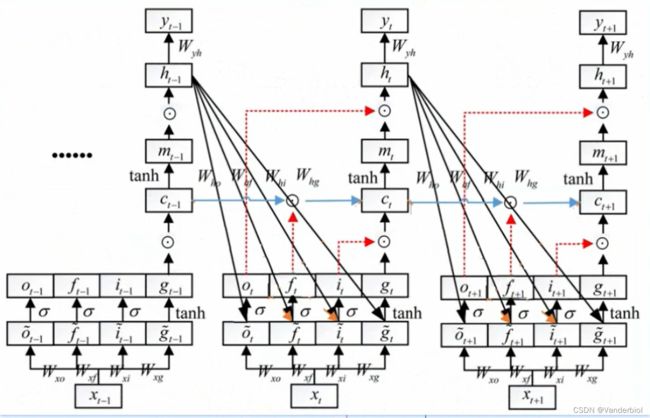
如图为LSTM与RNN结构对比
RNN
2.3单元结构
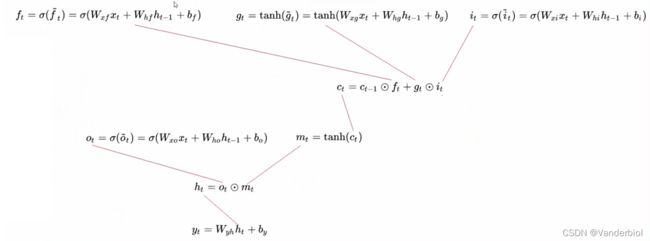
在LSTM每个时间步中,都有一个记忆细胞,这个东西给予了LSTM选择记忆功能,使得LSTM有能力自由选择每个时间步里面记忆的内容。
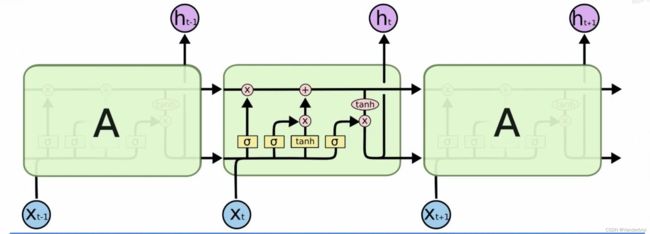
下图中Ct-1为上一个记忆细胞,ht-1为上一个时间点的状态,经过该单元,输出一个新的记忆细胞和一个新的状态。在单元中有三个![]() ,
,![]() 被称为门单元,它的输出值介于0-1之间。ft为遗忘门,it为更新门,Ot为输出门。
被称为门单元,它的输出值介于0-1之间。ft为遗忘门,it为更新门,Ot为输出门。
门是一种选择性地让信息通过的方法。它们由sigmoid神经网络层和逐点乘法运算组成。Sigmoid层输出0到1之间的数字,描述每个组件应允许通过多少。值为零表示“不让任何内容通过”,而值为 1 表示“允许所有信息通过”
公式所示为前向传播,Ct与Ct-1,ht-1,xt等参数都有关,其中Wxf,Whf,Wxi分别代表相应权重。在单元结构图中可以看出ft与Ct-1进行×运算(对应元素相乘),gt与it进行×运算,两者相加为新生成的ct。
2.4 缓解梯度爆炸和梯度消失
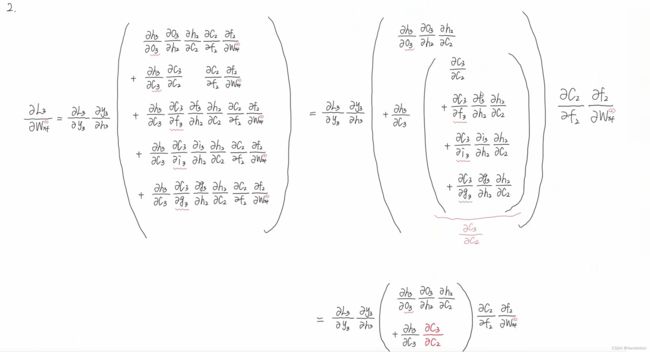
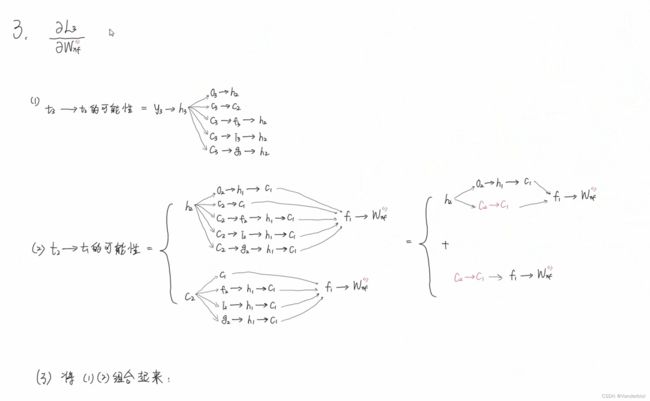
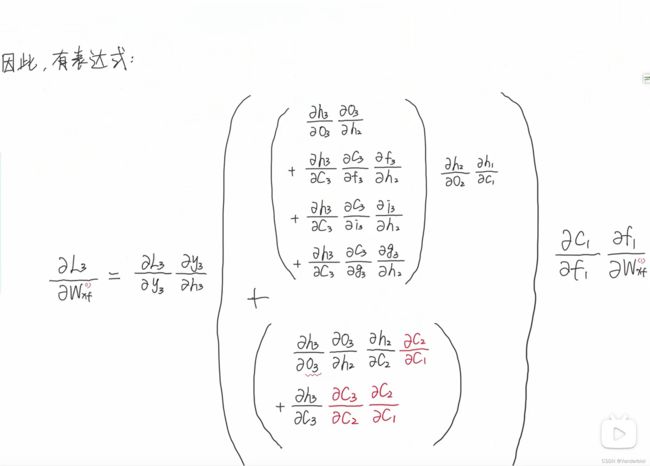
此过程为公式推导(以求Wxf为例)。
通过调节Whf,Whi,Whg的值,可以灵活控制Ct对Ct-1的偏导值,当要从n时刻长期记忆某个东西到m时刻时,该路径上的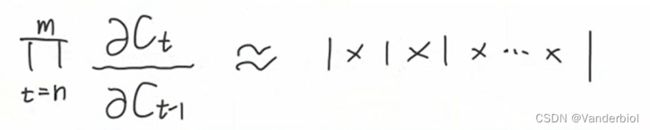
从而大大缓解了梯度消失和梯度爆炸。
(B站搜索老弓的学习日记,本篇博客为RNN与LSTM的学习笔记)