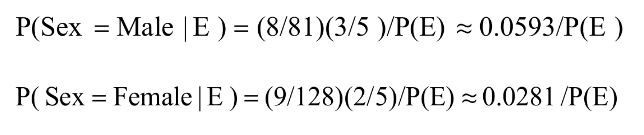数据挖掘基础

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

前言

数据挖掘基础
主要包含：决策树、关联规则、聚类分析、神经网络和统计分析。

一、数据挖掘定义及用途

1.定义：

数据挖掘是发现数据中潜在的有用的模式（信息、知识、规律、模型）的过程。

2.用途：

1、分类：
应用:评估信用卡申请者的风险等级-低、中、高。
方法:使用已知分类的实例建立分类模型，对未知分类的实例进行分类。
2、估值：
应用:根据购买模式，估计一个家庭的孩子个数、收入或财产。
*估值类似于分类,不同之处在于分类的输出是离散量，估值输出为连续值；分类的类别数确定，估值的量是不确定的。
3、预测：
应用:预测明天上证指数的收盘价
方法:通过历史数据得出预测模型，用该模型对未知变量的预测
4、聚类：
应用:在信用卡公司，发现输入属性的一-个集合，来区分接受寿险促销和未接受促销的持卡人.
方法:对实例分组，把相似的实例放在一个聚类中，发现最能区分各聚类的典型属性，使用这些属性开发预测未来结果的模型

二、决策树

1.理论知识

（1）概念

从数据产⽣决策树的机器学习技术称为决策树学习，简称决策树。
决策树是数据挖掘中最常⽤的⼀种分类和预测技术，使⽤其可建⽴分类和预测模型。

（2）算法一般过程（C4.5为例）

1）给定⼀个表示为“属性-值”格式的数据集T。数据集由多个具有多个输⼊
属性和⼀个输出属性的实例组成。
2）选择⼀个最能区别T中实例的输⼊属性，C4.5使⽤增益率来选择该属
性。
3）使⽤该属性创建⼀个树节点，同时创建该节点的分⽀，每个分⽀为该节
点的所有可能取值。
4）使⽤这些分⽀，将数据集中的实例进⾏分类，成为细分的⼦类。
5）将当前⼦类的实例集合设为T，对数据集中的剩余属性重复（2）（3）
步，直到满⾜以下两个条件之⼀时，该过程终⽌。创建⼀个叶⼦节点，该节点
为沿此分⽀所表达的分类类别，其值为输出属性的值。

该⼦类中的实例满⾜预定义的标准，如全部分到⼀个输出类中，或者分到⼀个输出类中的实例达到某个⽐例；没有剩余属性。

算法过程中设计到几种关键技术：

·选择最能区别数据集中实例属性的⽅法（信息增益率最⼤）
C4.5使用了信息论（Information Theory）的方法，即使用增益率（Gain Ratio）的概念来选择属性；目的是使树的层次和节点数最小，使数据的概化程度最大化。
C4.5选择的基本思想：选择具有最大增益率的属性作为分支节点来分类实例数据。

1）信息熵
信息变化的平均信息量称为“信息熵”（信息量化）
在信息论中，信息熵是信息的不确定程度的度量。熵越大，信息就越不容易搞清楚，需要的信息量就越大，能传输的信息就越多。

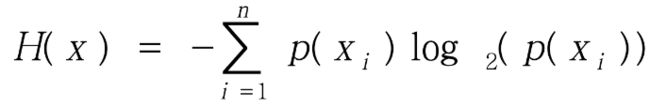2)信息增益
信息增益表示当x取属性xi值时，其对降低x的熵的贡献大小。信息增益值越大，越适于对x进行分类。C4.5使用信息量和信息增益的概念计算所有属性的增益，并计算所有属性的增益率，选择值最大的属性来划分数据实例

决策树计算实例1
决策树计算实例2

·剪枝方法
为控制决策树规模，优化决策树而采取的剪除部分分支的方法。分为预剪枝和后剪枝。

·检验方法
（1）use training set：使用在训练集实例上的预测效果进行检验。
（2）supplied test set：使用另外提供的检验集实例进行检验，此时需要单击 Set按钮来选择用来检验的数据集文件。
（3）cross-validation：使用交叉验证（Cross Validation，简称CV）来检验分类器，所用的折数填在Folds 文本框中。
（4）percent split：百分比检验。从数据集中按一定百分比取出部分数据作为检验集实例用，根据分类器在这些实例上的预测效果来检验分类器的质量。取出的数据量由“%” 栏中的值决定。

2.小结

优点
（1）容易被理解和被解释，并且可以被映射到一组更具吸引力的产生式规则。
（2）不需要对数据的性质作预先的假设。
（3）能够使用数值型数据和分类类型数据的数据集建立模型。
局限性
（1）输出属性必须是分类类型，且输出属性必须为一个。
（2）决策树算法是不稳定（Unstable）的。
（3）用数值型数据集创建的树较为复杂（如例2.3中的未剪枝的决策树），因为数值型数据的属性分裂通常是二元分裂。

三、关联规则

1.概述

关联分析（Association Analysis）
关联分析是发现事物之间关联关系（Associations）的分析过程。
典型应用——就是购物篮分析（Market Basket Analysis）。

购物篮分析
确定顾客在一次购物中可能一起购买的商品，发现其购物篮中不同商品之间的联系，分析顾客的购买习惯，从而发现购买行为之间的关联。
关联关系以一组特殊的规则形式出现——关联规则（Association Rules）

一般表现为蕴涵式规则形式：X→Y。
其中——
X和Y分别称为关联规则的前提或先导条件（Antecedent）和结果或后继（Consequent）。
关联规则与产生式规则有两点不同
（1）在某条关联规则中以前提条件出现的属性可以出现在下一条关联规则的结果中。
（2）传统的用于分类的产生式规则的结果中仅能有一个属性，而关联规则中则允许其结果包含一个或多个属性。

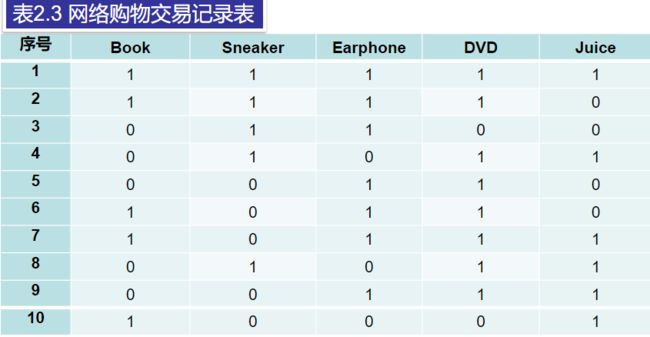若得到4条关联关系
（1）如果顾客购买了Sneaker（运动鞋），那么他们也会购买Earphone（耳机）。
（2）如果顾客购买了Book（图书），那么他们也会购买Juice（果汁）。
（3）如果顾客购买了Book（图书）和DVD，那么他们也会购买Earphone（耳机）。
（4）如果顾客购买了Book（图书）、Sneaker（运动鞋）和Earphone（耳机），那么他们也会购买DVD。

使用置信度度量每个关联规则在前提条件下结果发生的可能性。
关联关系（1）的置信度为：3/5 = 60%。

使用支持度度量包含了关联关系中出现的属性值的交易占所有交易的百分比。
关联关系（1）的支持度为：3/10 = 30%

关联分析过程中设置置信度和支持度的阈值，当得到的关联关系达到置信度和支持度的阈值时，这样的关联关系被认为是有趣的，而保留下来应用到实际问题中。

2.关联分析

Apriori算法基本思想：
（1）生成条目集（Item Sets）。条目集是符合一定的支持度要求的“属性-值”的组合。那些不符合支持度要求的“属性-值”组合被丢弃，因此，规则的生成过程可以在合理的时间内完成。
（2）使用生成的条目集创建一组关联规则。

例：将表2.3作为数据集，使用Apriori算法进行关联分析，产生描述网络购买行为的关联规则。
步骤：
（1）设置支持度阈值为50%，创建第一个条目集表，包含单项条目
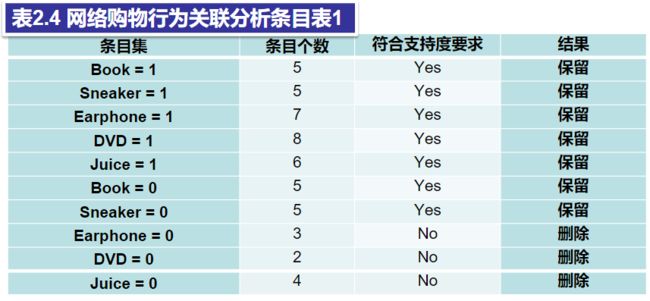（2）设置支持度阈值为40%，创建第二个条目集表，包含双项条目

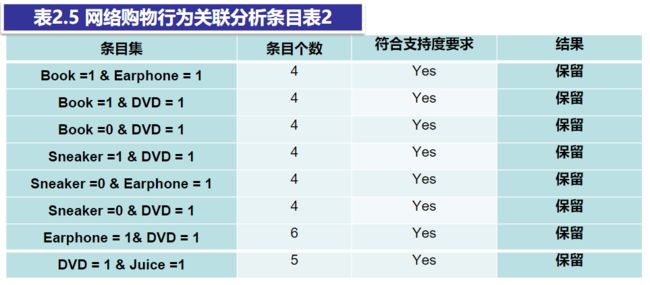
（3）仍将支持度阈值设置为40%，使用双项条目表中的“属性-值”组合生成三项条目集，有两条条目。
Book =1 & Earphone = 1& DVD = 1
Sneaker =0 & Earphone = 1 & DVD = 1

（4）再次将支持度阈值设置为40%，以三项条目集为基础，生成四项条目集，没有符合支持度要求的条目，条目集生成工作结束。

5）以生成的条目集为基础创建关联规则。
首先设置置信度阈值为80%；
然后从双项和三项条目集表中生成关联规则；
最后，所有不满足置信度阈值的规则将被删除。
以双项条目集中的第一条条目生成的两条规则——
IF Book =1 THEN Earphone = 1 （置信度：4/5 = 80%，保留）
IF Earphone = 1 THEN Book =1（置信度：4/7 = 57.1%，删除）
以三项条目集中的第一条条目生成的三条规则——
IF Book =1 & Earphone = 1 THEN DVD = 1（置信度：4/4 = 100%，保留）
IF Book =1 & DVD = 1 THEN Earphone = 1（置信度：4/4 = 100%，保留）
IF Earphone = 1 & DVD = 1 THEN Book =1（置信度：4/6 = 66.7%，删除）

3.小结

优势
关联规则不受因变量个数的限制，能够在大型数据库中发现数据之间的关联关系，所以其应用非常广泛。

局限性
一次关联分析输出的规则往往数量较多，且多数并无利用价值，所以对关联规则的解释和应用必须谨慎。

四、聚类分析（K-means）

将多个无明显分类特征的对象，按照某种相似性分成多个簇（Cluster）的分析过程。目前有许多聚类算法和技术（ 统计技术）。

1.K-means算法（K-均值算法）

最著名、应用最广泛、聚类效果也很好。斯图尔特·劳埃德（Stuart Lloyd）于1982年提出的简单而有效的统计聚类技术。
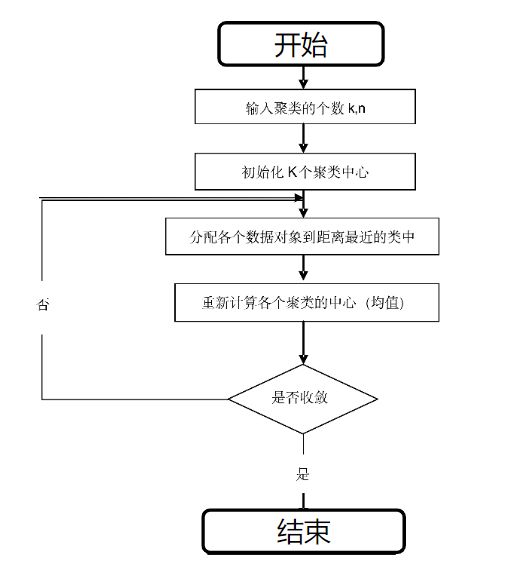
基本思想：

（1）随机选择一个K值，用以确定簇的总数。

（2）在数据集中任意选择K个实例，将它们作为初始的簇中心。

（3）计算这K个簇中心与其它剩余实例的简单欧氏距离（Euclidean Distance）。用这个距离作为实例之间相似性的度量，将与某个簇相似度高的实例划分到该簇中，成为其成员之一。

（4）使用每个簇中的实例来计算该簇新的簇中心。

（5）如果计算得到新的簇中心等于上次迭代的簇中心，终止算法过程。否则，用新的簇中心作为簇中心并重复步骤（3）~（5）。

例：对表2.6中的数据进行K-means聚类分析。

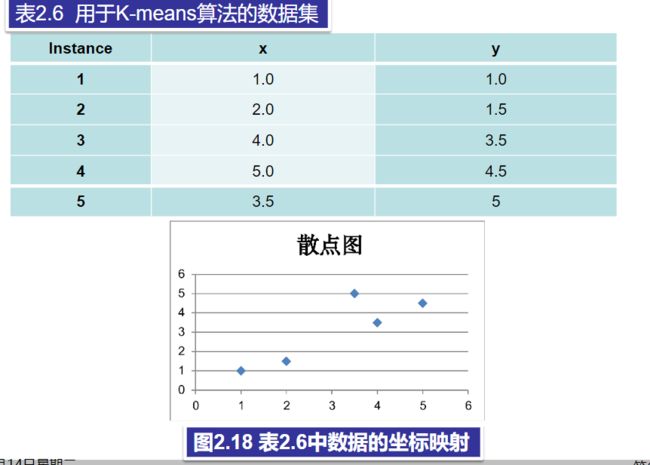
（1）设置 K 值为2。

（2）任意选择两个点分别作为两个簇的初始簇中心。假设选择实例1作为第1个簇中心，实例2作为第2个簇中心。

（3）使用式2.9，计算其余实例与两个簇中心的简单欧氏距离（Euclidean Distance），结果如表2.7所示。

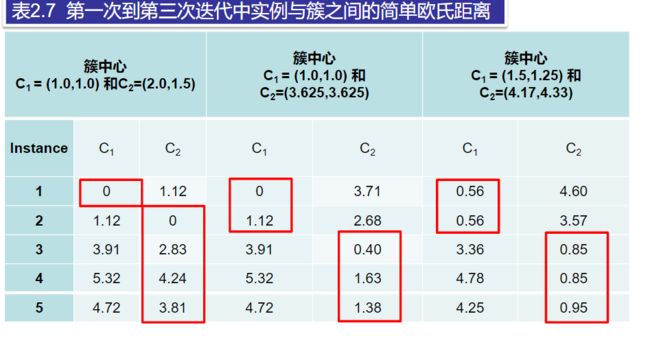（4）重新计算新的簇中心。
对于簇1簇中心不变，即C1 = (1.0,1.0)。
对于簇2：x = (2.0+4.0+5.0+3.5) / 4 = 3.625，y = (1.5+3.5+4.5+5) / 4 = 3.625。
得到新的簇中心C1= (1.0,1.0) 和 C2= (3.625,3.625)，因为簇中心发生了变化，算法必须执行第二次迭代，重复步骤（3）。
第二次迭代之后的结果导致了簇的变化：{1,2}和{3,4,5}。

（5）重新计算每个簇中心。
对于簇1：x = (1.0+2.0) / 2= 1.5，y = (1.0+1.5) / 2 = 1.25。
对于簇2：x = (2.0+5.0+3.5) / 3= 4.17，y = (3.5+4.5+5) / 3 = 4.33。
这次迭代后簇中心再次改变。因此，该过程继续进行第三次迭代，结果形成{1,2}和{3,4,5}两个簇，与第二次迭代后形成的簇完全一样。若继续计算新簇中心的话，簇中心的值一定不变。至此，算法结束。

2.小结

优势
非常受欢迎的算法，容易理解，实现简单。

局限性
（1）只能处理数值型数据，若数据集中有分类类型的属性，要么将该属性删除，要么将其转换成等价的数值数据。
（2）算法开始前，需要随机选择K值作为初始的簇个数（带有随意性，错误的选择将影响聚类效果）。通常选择不同的K值进行重复实验，期望找到最佳K值。
（3）当簇的大小近似相等时，K-means算法的效果最好。
（4）对于聚类贡献不大的属性可能会对聚类效果造成影响（孤立点）。在聚类之前需对属性进行选择。
（5）簇的解释困难。可使用有指导的挖掘工具对无指导聚类算法所形成簇的性质作进一步的解释。

五、数据库中的知识发现（KDD）

从数据集中提取可信的、新颖的、具有潜在使用价值的能够被人类所理解的模式的非繁琐的处理过程。

KDD一词是Usama M.Fayyad于1989年首次提出，并给出如上定义。
定义解析
KDD——一个处理过程，大部分步骤是系统自动执行的；
数据集——一个有关事实的集合；
模式——针对某个数据集，描述了数据自身的特性；
可信的——要求发现的模式必须经过了正确性检验，能够应用到新数据中；
新颖的——表示发现的模式应该是以前没有发现的、希望得到的新发现；
潜在使用价值——表示发现的模式应该有价值、有意义，价值和意义一般不能直接从数据中看出来或查询和搜索出来，是可以被利用的潜在价值；
可被人理解——发现的模式是人们容易理解的，从而更好的被评估和利用。

1.KDD过程

1、经典模型（阶梯处理模型，Fayyad等提出，9步骤）——
（1）数据准备——了解应用领域情况，熟悉背景知识，确定用户要求。
（2）数据选择——根据用户要求从数据库中提取与KDD相关的数据，会利用一些数据库操作对数据进行处理。
（3）数据预处理——对数据进行加工，检查数据的完整性及数据的一致性，对其中的噪声数据、缺失数据进行处理。
（4）数据缩减——对经过预处理的数据，根据知识发现的任务对数据进行再处理，主要通过投影或数据库中的其他操作减少数据量。
（5）确定KDD的目标——根据用户要求，确定KDD是发现何种类型的知识。
（6）确定知识发现算法——根据目标选择合适的知识发现算法，包括选取合适的模型和参数，并使得知识发现算法与整个KDD的评价标准相一致。
（7）数据挖掘——运用算法，从数据中提取出用户所需要的知识。
（8）模式解释——对发现的模式进行解释。为了取得更为有效的知识，可能会返回到前面处理步骤中反复进行前面的KDD过程，从而提取出更有效的知识。
（9）知识评价——将发现的知识以用户能理解的方式呈现，同时对知识进行检验和评估。

2、CRISP-DM模型（Cross Industry Standard Process for Data Mining，跨行业数据挖掘标准流程，6个步骤）。
（1）商业理解（Business understanding）——关注项目目标和商业前景的需求。给出了数据挖掘问题的定义和最初的计划。
（2）数据理解（Data understanding）——数据的收集和假设的构造。
（3）数据准备（Data preparation）——选择表、记录和属性，为所选的模型工具清洗数据。
（4）建模（Modeling）——选择和应用一个或多个数据挖掘技术。
（5）评估（Evaluation）——通过对发现的结果进行分析，判断开发的模型是否达到了商业目标，同时确定该模型未来的使用价值。
（6）部署（Deployment）——若模型达到了商业目标，制定行动计划应用模型。

2.KDD应用

应用1.商业理解
1、任务——确定商业目标
2、任务——评估形势
3、任务——确定KDD目标
4、任务——制定项目计划

应用2.数据理解
1、任务——收集和描述数据
2、任务——探查数据

应用3.数据准备
·从数据库抽取数据

·清洗数据
1）噪声数据处理
噪声（Noise）——属性值中的随机错误。
处理噪声——发现和处理重复记录和错误属性值；采取数据平滑操作；发现和处理孤立点。

数据平滑
一种减少数据中噪声的处理技术。
分箱方法、均值平滑、中值平滑、函数平滑、线性拟合方法等。
分箱方法——将数据进行排序，并对它们进行“等高度”划分成若干个箱，每箱中数据个数相同，再根据箱中数据均值、中值或边界接近值进行平滑
聚类分析技术——发现并尽可能从数据集中删除非典型实例，即孤立点。

2）缺失数据处理
产生原因——遗漏；无法填写。
处理办法——
忽略含有缺失值的记录；
手工填补缺失值；
利用均值代替缺失值；
利用同类均值填补缺失属性值；
使用全部常量填补缺失值；
利用最可能的值填补缺失值。

·变换数据：数据标准化
4 种常用的标准化方法——

十进制缩放（Decimal scaling）
将数据值除以10的整数次方。例如，若某属性的取值范围（旧域）为[-1000,1000]之间，则可以每个值除以1000使得取值范围变为[-1,1]（新域）之间。

Min-Max标准化（Min-Max normalization）
适应于属性的最小值和最大值都已知的情况。其计算公式为
新值=[原值-旧域最小值（新域最大值-新域最小值）+新域最小值]/（旧域最大值-旧域最小值）

Z-Score标准化（Normalization using Z-scores）
将属性值转换为标准值。此方法是将该值减去属性平均值（u）再除以属性值的标准差（sigma），公式如下
新值=（旧值-u）/sigma

对数标准化（Logarithmic normalization）
用一些值的以2为底的对数值代替原值可以缩放值域，而又不丢失信息。例如，以2为底的64的对数为6，即2的6次方为64，则使用6代替64。

应用4.建模

建立一个有指导学习或无指导聚类模型的典型步骤：
（1）从准备好的数据集实例中选择训练和检验数据；
（2）选择一组输入属性；
（3）如果学习是有指导的，选择一个或多个输出属性；
（4）选择学习参数的值；
（5）调用数据挖掘工具建立模型。
（6）数据挖掘完成，对模型进行评估。如果结果不够理想，可以多次重复上述步骤。

六、评估技术

1.数据集划分

① Hold-Out方法
将数据集随机划分为训练集和检验集。此方法处理简单，但是其随机性地划分训练集和检验集，并未达到交叉检验的目的，其检验结果受数据集随机分组的影响较大，所以这种方法的检验效果并不具有说服力。

② k-折交叉检验（k-CV）
将数据集分成k组( 一般均分， 且大于等于2)， 将每组数据分别做一次检验集对由其余k-1组数据作为训练集建立的模型进行检验，将这k个检验的检验集分类正确率的平均值作为该模型的平均性能度量。k折交叉检验可以有效地避免模型训练不够或训练过度状态的发生，检验结果比较有说服力。Weka中的交叉检验方法即为k-折交叉检验。

③ Leave-One-Out交叉检验（LOO-CV）
设数据集有n个实例，则LOO-CV即为n-CV。它是将每个实例单独作为验证集，对由其余n-1个实例作为训练集建立的模型进行检验，将这n个检验的检验集分类正确率的平均值作为该模型的性能度量。此方法因其每次建模都使用了几乎所有的数据集实例，其分布与完整数据集相同，故模型结果更为可靠。同时训练和检验过程中无随机变量的影响，检验结果稳定。但这种交叉检验方法因建立的模型数量与数据集实例个数相同，成本太大，在实际应用中k-折交叉检验更具优势。

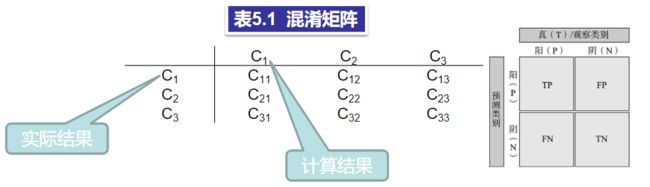
2.混淆矩阵和正确率

混淆矩阵和分类正确率
混淆矩阵（Confusion Matrix）是评估有指导学习模型的基本工具，它能够直观的给出模型检验集分类正确或错误的情况。
混淆矩阵是机器学习中一种分类效果可视化工具，表现为一个二维表矩阵。表中的C1、C2、和C3表示模型有三个分类，C11、C12、……、C33表示分类到三个分类中的数据实例的个数。

统计学方法

3.评估有指导的学习模型

数值型输出的准确率度量常用方法
平均绝对误差（Mean Absolute Error，MAE）
均方误差（Mean Squared Error，MSE）
均方根误差（Root Mean Squared Error，RMS）

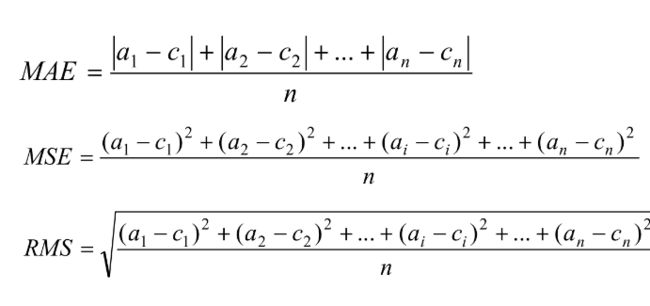
数值型属性的冗余检查
相关系数 (Correlation Coefficient)
度量了两个数值型属性之间的线性相关程度，对于样本用r或ρ表示，对于总体则用希腊字母rho表示。
相关系数的值介于[-1,1]之间。
正相关（Positive Correlation）
两个属性具有同时增加或减少的特性，r接近于1。
负相关（Negative Correlation）
一个属性增加而同时另一个属性减少的特性，r接近于-1。
如果r接近于0，则表示两个属性不具有线性相关性。
使用显著性检验，来排除相关性联系偶然出现的可能。
属性正向或负向高度相关，则选择其中的一个用于数据挖掘。

4.评估无指导聚类模型

最一般考虑：簇质量的度量。
计算每个簇中实例与其簇中心之间的误差平方和。
误差平方和越小，簇的质量越高。

使用有指导学习技术
步骤——
（1）建立无指导聚类模型，将每个簇作为一个类；
（2）从每个类中随机选择1个实例样本；
（3）将随机选取的实例作为训练数据，创建以这些类为输出属性的有指导学习模型，使用剩余的实例作为检验集实例检验有指导模型的分类正确率；
（4）观察有指导模型的分类正确率，若分类性能较好说明聚类簇定义良好；若分类正确率较低，说明聚类簇没有明确的定义。

七、神经网络

---

---

八、统计技术

1.回归分析

一种统计分析方法
用来确定两个或两个以上变量之间的定量的依赖关系，并建立一个数学方程作为数学模型，来概化一组数值数据，进而进行数值数据的估值和预测，应用非常广泛。

分类：
一元回归分析和多元回归分析
线性回归分析和非线性回归分析

（1）简单线性回归分析

只有一个自变量作为因变量的预测。
典型的斜截式（Slope-Intercept Form）方程：y=ax+c。

其中
X——自变量，y——因变量，a和c——常量；
方程的图形是斜率为a，y轴截距为c的一条直线。
常量a和c的确定，是建立回归方程的重要工作，称为参数估计（Parametric Estimating）。
常用的计算a和b的统计学方法是最小二乘法（Least-Squares Criterion）。
最小二乘法
又称最小平方法。
通过使得因变量预测值与实际值之间的误差的平方和（方差）最小，而得出a和c的最优解。

（2）多元线性回归

有两个或两个以上的自变量的线性回归，由多个自变量的最优组合共同来预测或估计因变量，结果更有效、更准确，更符合实际需要。

(3)非线性回归

线性和非线性回归分析都是使用最小二乘法进行回归分析，区别只是分析的问题中变量之间的关系呈线性的和非线性的。
常见的非线性回归分析模型：指数曲线方程、对数曲线方程、幂函数曲线方程、抛物线曲线方程、双曲线方程、S形曲线方程与logistic曲线方程等

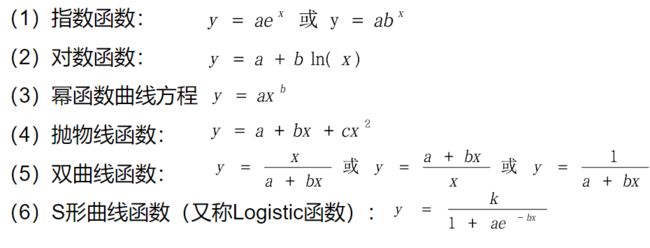
步骤：
（1）选择适当的非线性回归方程。
（2）通过变量置换，将非线性回归转换为线性回归，利用线性回归方法进行参数估计（式7.8）。
（3）评估非线性模型。

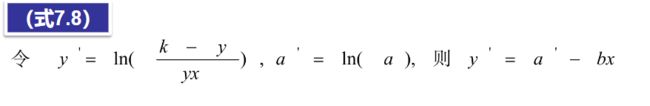
2.贝叶斯分类器

·一种参数估计方法。
·将关于未知参数的先验信息与样本信息相结合，根据贝叶斯公式，得出后验信息，然后根据后验信息去推断未知参数。
·在决策支持、风险评估、模式识别等方面都得到了很广泛的应用，被用来建立分类模型，就是著名的贝叶斯分类器（式7.13）
·贝叶斯分类器（Bayes Classifier）
一种简单、功能强大的有指导分类技术。
假定所有输入属性的重要性相等，且彼此是独立的。
其中——
H为要检验的假设，E为与假设相关的数据样本。
从分类的角度考察——
假设H就是因变量，代表着预测类；
数据样本E是输入实例属性值的集合；
P（E | H）是给定输入实例属性值E时，假设H为真的条件概率；
P（H）为先验概率（priori probability），表示在任何输入属性值E出现之前假设的概率。
条件概率和先验概率可以通过训练数据计算出来。

例：

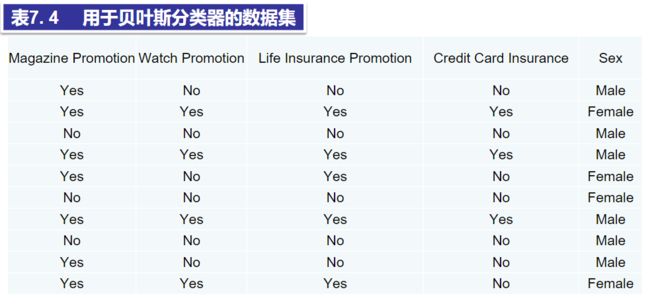
（1）找出先验信息。
将Sex作为输出属性。
表7.5依据表7.4，计算类实例个数与实例总数之比，得出每个输入属性的输出属性值的分布。

（2）确定要检验的假设。
要检验的假设H有两个：客户Sex为Male；客户Sex为Female。
要判断新客户的性别Sex，比较两个概率值 和 的大小，概率值大的，其假设H成立。

（3）计算
和
两个概率值。
计算贝叶斯公式（式7.13）中的条件概率P（E | H）、先验概率P（H）和P（E），即计算P(E | Sex = Male ) 、P(E | Sex = female )、P(sex = male )、P(Sex = Female ) 和 Sex=Male 及 Sex=Female 的样本数据出现的概率P（E）。
可认为样本集中男女出现比例相同，则两个P（E）值相等。

（4）根据贝叶斯公式计算两个P（H | E），即P(Sex = Male | E )和P(Sex = Female | E )，比较两个概率值，概率值较大的假设H成立

结论
在P(E) 值相同的情况下，因为0.0593 > 0.0281，则新实例的Sex最可能为Male。