完美解决共线性数据的问题
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
import statsmodels.stats.outliers_influence
from statsmodels.stats.outliers_influence import variance_inflation_factor
Ols
data=pd.read_csv("C:/Users/可乐怪/Desktop/线性回归2021/linear2021.csv")
data.insert(4,'constant',1)
model=sm.OLS(data['y'],data.iloc[:,:5]).fit()
print(model.summary())
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.542
Model: OLS Adj. R-squared: 0.501
Method: Least Squares F-statistic: 13.32
Date: Wed, 22 Dec 2021 Prob (F-statistic): 3.07e-07
Time: 13:22:25 Log-Likelihood: -64.548
No. Observations: 50 AIC: 139.1
Df Residuals: 45 BIC: 148.7
Df Model: 4
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
x1 0.7096 0.469 1.513 0.137 -0.235 1.654
x2 0.5776 1.498 0.386 0.702 -2.439 3.594
x3 0.6079 1.476 0.412 0.682 -2.365 3.581
x4 1.0829 0.271 3.995 0.000 0.537 1.629
constant 2.6947 0.620 4.348 0.000 1.447 3.943
==============================================================================
Omnibus: 0.050 Durbin-Watson: 1.891
Prob(Omnibus): 0.975 Jarque-Bera (JB): 0.229
Skew: -0.041 Prob(JB): 0.892
Kurtosis: 2.679 Cond. No. 42.7
==============================================================================
VIF>10,存在多共线性
from statsmodels.stats.outliers_influence import variance_inflation_factor
vif=[]
for i in range(4):
a=round(variance_inflation_factor(data.iloc[:,:5].values,i),2)
vif.insert(i,a)
print(vif)
[10.42, 30.38, 36.02, 1.08]
Ridge 回归
标准化数据做回归
data_scale=pd.DataFrame()
from sklearn import preprocessing
data_scale['y'] =preprocessing.scale(data['y'])
data_scale['x1'] =preprocessing.scale(data['x1'])
data_scale['x2'] =preprocessing.scale(data['x2'])
data_scale['x3'] =preprocessing.scale(data['x3'])
data_scale['x4']=preprocessing.scale(data['x4'])
data_scale.insert(1,'constant',1)
model2=sm.OLS(data_scale['y'],data_scale.iloc[:,2:]).fit()
print(model2.summary())
OLS Regression Results
=======================================================================================
Dep. Variable: y R-squared (uncentered): 0.542
Model: OLS Adj. R-squared (uncentered): 0.502
Method: Least Squares F-statistic: 13.62
Date: Wed, 22 Dec 2021 Prob (F-statistic): 2.12e-07
Time: 13:51:57 Log-Likelihood: -51.417
No. Observations: 50 AIC: 110.8
Df Residuals: 46 BIC: 118.5
Df Model: 4
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
x1 0.4926 0.322 1.530 0.133 -0.156 1.141
x2 0.2144 0.550 0.390 0.698 -0.893 1.321
x3 0.2493 0.599 0.416 0.679 -0.956 1.454
x4 0.4191 0.104 4.039 0.000 0.210 0.628
==============================================================================
Omnibus: 0.050 Durbin-Watson: 1.891
Prob(Omnibus): 0.975 Jarque-Bera (JB): 0.229
Skew: -0.041 Prob(JB): 0.892
Kurtosis: 2.679 Cond. No. 12.2
==============================================================================
from sklearn.linear_model import Ridge
k=np.linspace(0,1,100)#(start, end, num=num_points)使k属于[0,1]
y=data_scale['y']
x=data_scale.iloc[:,2:]
θ1=[]
θ2=[]
θ3=[]
θ4=[]
for i in range(len(k)):
ridge = Ridge(k[i])
ridge =ridge .fit(x, y)
θ1.append(ridge.coef_[0])
θ2.append(ridge.coef_[1])
θ3.append(ridge.coef_[2])
θ4.append(ridge.coef_[3])
plt.plot(k,θ1,'r',alpha=0.5,)
plt.plot(k,θ2,'b-.',alpha=0.5)
plt.plot(k,θ3,'y+')
plt.plot(k,θ4,'m+')
plt.xlabel('k',size=15)
plt.ylabel('θj(k)',size=15)
plt.legend(['θ1', 'θ2', 'θ3','θ4'], loc='upper right')
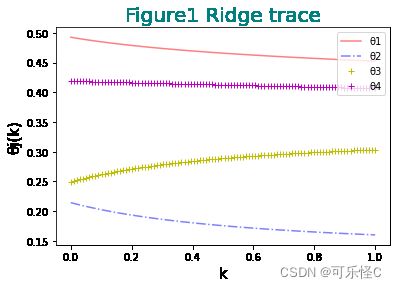
plt.title('Figure1 Ridge trace',size=20,c='teal')
plt.show()
由Ridge trace可知去除x2然后做回归
model2=sm.OLS(data['y'],data[['x1','x4','x3']]).fit()
print(model2.summary())
OLS Regression Results
=======================================================================================
Dep. Variable: y R-squared (uncentered): 0.968
Model: OLS Adj. R-squared (uncentered): 0.966
Method: Least Squares F-statistic: 480.7
Date: Wed, 22 Dec 2021 Prob (F-statistic): 2.94e-35
Time: 14:01:26 Log-Likelihood: -73.676
No. Observations: 50 AIC: 153.4
Df Residuals: 47 BIC: 159.1
Df Model: 3
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
x1 0.5201 0.191 2.725 0.009 0.136 0.904
x4 2.1311 0.151 14.160 0.000 1.828 2.434
x3 1.7593 0.277 6.362 0.000 1.203 2.316
==============================================================================
Omnibus: 0.426 Durbin-Watson: 2.274
Prob(Omnibus): 0.808 Jarque-Bera (JB): 0.584
Skew: -0.110 Prob(JB): 0.747
Kurtosis: 2.518 Cond. No. 4.63
==============================================================================
拟合完美R^2=0.968
数据文件
链接:https://pan.baidu.com/s/12rI3jTX0cQ6UQu_R1jQpDA
提取码:hd5k