PCL中3D点云特征描述与提取(三)
PCL中3D点云特征描述与提取(三)
- 1 如何从一个深度图像中提取NARF特征
- 2 RoPs特征
-
- 2.1 理论基础
-
- 2.1.1 生物视觉认知学启示
- 2.1.2 局部参考坐标框架构建
- 2.1.3 RoPS特征描述
- 2.1.4 推荐算法参数及说明
- 2.2 PCL应用实例详解
- 3 基于惯性矩与偏心率的描述子
-
- 3.1 理论基础
- 3.2 源代码解析
- 4 BoundaryEstimation 进行边界提取
1 如何从一个深度图像中提取NARF特征
本小节将演示如何从一个深度图像中提取NARF特征点位置的NARF特征描述子。可执行程序能够加载一个点云(如果用户没有给定,则自动创建随机点云),从中提取特征点,然后在这些位置估算特征描述子,接着在一个深度图像和三维视图中可视化这些特征点位置。
首先创建一个工作空间narf_feature_extraction,然后再在工作空间创建一个文件夹src用于存放源代码:
mkdir -p narf_feature_extraction/src
接着,在narf_feature_extraction/src路径下,创建一个文件并命名为narf_feature_extraction.cpp,拷贝如下代码:
/* \author Bastian Steder */
#include \n\n"
<< "Options:\n"
<< "-------------------------------------------\n"
<< "-r angular resolution in degrees (default " <<angular_resolution<<")\n"
<< "-c coordinate frame (default " << (int)coordinate_frame<<")\n"
<< "-m Treat all unseen points to max range\n"
<< "-s support size for the interest points (diameter of the used sphere - "
"default "<<support_size<<")\n"
<< "-o <0/1> switch rotational invariant version of the feature on/off"
<< " (default "<< (int)rotation_invariant<<")\n"
<< "-h this help\n"
<< "\n\n";
}
void setViewerPose (pcl::visualization::PCLVisualizer& viewer, const Eigen::Affine3f& viewer_pose)
{
Eigen::Vector3f pos_vector = viewer_pose * Eigen::Vector3f (0, 0, 0);
Eigen::Vector3f look_at_vector = viewer_pose.rotation () * Eigen::Vector3f (0, 0, 1) + pos_vector;
Eigen::Vector3f up_vector = viewer_pose.rotation () * Eigen::Vector3f (0, -1, 0);
viewer.setCameraPosition(pos_vector[0],
pos_vector[1],
pos_vector[2],
look_at_vector[0],
look_at_vector[1],
look_at_vector[2],
up_vector[0],
up_vector[1],
up_vector[2]);
}
int main (int argc, char** argv)
{
/* 解析命令行参数 */
if (pcl::console::find_argument (argc, argv, "-h") >= 0)
{
printUsage (argv[0]);
return 0;
}
if (pcl::console::find_argument (argc, argv, "-m") >= 0)
{
setUnseenToMaxRange = true;
cout << "Setting unseen values in range image to maximum range readings.\n";
}
if (pcl::console::parse (argc, argv, "-o", rotation_invariant) >= 0)
{
cout << "Switching rotation invariant feature version "<< (rotation_invariant ? "on" : "off")<<".\n";
}
int tmp_coordinate_frame;
if (pcl::console::parse (argc, argv, "-c", tmp_coordinate_frame) >= 0)
{
coordinate_frame = pcl::RangeImage::CoordinateFrame (tmp_coordinate_frame);
cout << "Using coordinate frame "<< (int)coordinate_frame<<".\n";
}
if (pcl::console::parse (argc, argv, "-s", support_size) >= 0)
{
cout << "Setting support size to "<<support_size<<".\n";
}
if (pcl::console::parse (argc, argv, "-r", angular_resolution) >= 0)
{
cout << "Setting angular resolution to "<<angular_resolution<<"deg.\n";
}
angular_resolution = pcl::deg2rad (angular_resolution);
/* 读取pcd文件,或者如果没有给出,则创建一个样本点云 */
pcl::PointCloud<PointType>::Ptr point_cloud_ptr (new pcl::PointCloud<PointType>);
pcl::PointCloud<PointType>& point_cloud = *point_cloud_ptr;
pcl::PointCloud<pcl::PointWithViewpoint> far_ranges;
Eigen::Affine3f scene_sensor_pose (Eigen::Affine3f::Identity ());
std::vector<int> pcd_filename_indices = pcl::console::parse_file_extension_argument (argc, argv, "pcd");
if (!pcd_filename_indices.empty ())
{
std::string filename = argv[pcd_filename_indices[0]];
if (pcl::io::loadPCDFile (filename, point_cloud) == -1)
{
cerr << "Was not able to open file \""<<filename<<"\".\n";
printUsage (argv[0]);
return 0;
}
scene_sensor_pose = Eigen::Affine3f (Eigen::Translation3f (point_cloud.sensor_origin_[0],
point_cloud.sensor_origin_[1],
point_cloud.sensor_origin_[2])) *
Eigen::Affine3f (point_cloud.sensor_orientation_);
std::string far_ranges_filename = pcl::getFilenameWithoutExtension (filename)+"_far_ranges.pcd";
if (pcl::io::loadPCDFile (far_ranges_filename.c_str (), far_ranges) == -1)
{
std::cout << "Far ranges file \""<<far_ranges_filename<<"\" does not exists.\n";
}
}
else
{
setUnseenToMaxRange = true;
cout << "\nNo *.pcd file given => Genarating example point cloud.\n\n";
for (float x=-0.5f; x<=0.5f; x+=0.01f)
{
for (float y=-0.5f; y<=0.5f; y+=0.01f)
{
PointType point; point.x = x; point.y = y; point.z = 2.0f - y;
point_cloud.points.push_back (point);
}
}
point_cloud.width = (int) point_cloud.points.size (); point_cloud.height = 1;
}
/* 从点云中创建深度图像 */
float noise_level = 0.0;
float min_range = 0.0f;
int border_size = 1;
boost::shared_ptr<pcl::RangeImage> range_image_ptr (new pcl::RangeImage);
pcl::RangeImage& range_image = *range_image_ptr;
range_image.createFromPointCloud (point_cloud,
angular_resolution,
pcl::deg2rad (360.0f),
pcl::deg2rad (180.0f),
scene_sensor_pose,
coordinate_frame,
noise_level,
min_range,
border_size);
range_image.integrateFarRanges (far_ranges);
if (setUnseenToMaxRange)
{
range_image.setUnseenToMaxRange ();
}
/* 打开3D可视化窗口,并添加点云 */
pcl::visualization::PCLVisualizer viewer ("3D Viewer");
viewer.setBackgroundColor (1, 1, 1);
pcl::visualization::PointCloudColorHandlerCustom<pcl::PointWithRange> range_image_color_handler (range_image_ptr, 0, 0, 0);
viewer.addPointCloud (range_image_ptr, range_image_color_handler, "range image");
viewer.setPointCloudRenderingProperties (pcl::visualization::PCL_VISUALIZER_POINT_SIZE, 1, "range image");
viewer.initCameraParameters ();
setViewerPose (viewer, range_image.getTransformationToWorldSystem ());
/* 显示深度图像 */
pcl::visualization::RangeImageVisualizer range_image_widget ("Range image");
range_image_widget.showRangeImage (range_image);
/* 提取NARF关键点 */
pcl::RangeImageBorderExtractor range_image_border_extractor;
pcl::NarfKeypoint narf_keypoint_detector;
narf_keypoint_detector.setRangeImageBorderExtractor (&range_image_border_extractor);
narf_keypoint_detector.setRangeImage (&range_image);
narf_keypoint_detector.getParameters ().support_size = support_size;
pcl::PointCloud<int> keypoint_indices;
narf_keypoint_detector.compute (keypoint_indices);
std::cout << "Found "<<keypoint_indices.points.size ()<<" key points.\n";
// -----在深度图像窗口显示关键点-----
//for (size_t i=0; i
//range_image_widget.markPoint (keypoint_indices.points[i]%range_image.width,
//keypoint_indices.points[i]/range_image.width);
/* 在三维视图中显示关键点 */
pcl::PointCloud<pcl::PointXYZ>::Ptr keypoints_ptr (new pcl::PointCloud<pcl::PointXYZ>);
pcl::PointCloud<pcl::PointXYZ>& keypoints = *keypoints_ptr;
keypoints.points.resize (keypoint_indices.points.size ());
for (size_t i=0; i<keypoint_indices.points.size (); ++i)
{
keypoints.points[i].getVector3fMap () = range_image.points[keypoint_indices.points[i]].getVector3fMap ();
}
pcl::visualization::PointCloudColorHandlerCustom<pcl::PointXYZ> keypoints_color_handler (keypoints_ptr, 0, 255, 0);
viewer.addPointCloud<pcl::PointXYZ> (keypoints_ptr, keypoints_color_handler, "keypoints");
viewer.setPointCloudRenderingProperties (pcl::visualization::PCL_VISUALIZER_POINT_SIZE, 7, "keypoints");
/* 为特征点提取NARF描述子 */
std::vector<int> keypoint_indices2;
keypoint_indices2.resize (keypoint_indices.points.size ());
for (unsigned int i=0; i<keypoint_indices.size (); ++i)
{
keypoint_indices2[i]=keypoint_indices.points[i]; //要得到正确的向量类型,这一步是必要的
}
pcl::NarfDescriptor narf_descriptor (&range_image, &keypoint_indices2);
narf_descriptor.getParameters ().support_size = support_size;
narf_descriptor.getParameters ().rotation_invariant = rotation_invariant;
pcl::PointCloud<pcl::Narf36> narf_descriptors;
narf_descriptor.compute (narf_descriptors);
cout << "Extracted "<<narf_descriptors.size ()<<" descriptors for "
<<keypoint_indices.points.size ()<< " keypoints.\n";
cout << narf_descriptors << endl;
while (!viewer.wasStopped ())
{
range_image_widget.spinOnce ();
viewer.spinOnce ();
pcl_sleep(0.01);
}
}
【解释说明】
下面对上述源代码的关键语句进行解释说明,首先解析命令行参数,读取一个点(如果没有给出则自行创建一个点云),然后创建一个深度图像并从中提取NARF关键点,所有这些步骤在之前的NARF关键点提取中已经涉及了。
std::vector<int> keypoint_indices2;
keypoint_indices2.resize (keypoint_indices.points.size ());
for (unsigned int i=0; i<keypoint_indices.size (); ++i)
{
keypoint_indices2[i]=keypoint_indices.points[i]; //要得到正确的向量类型,这一步是必要的
}
此处,我们建立NARF关键点索引的向量,此矢量作为NARF特征计算的输入来使用。
pcl::NarfDescriptor narf_descriptor (&range_image, &keypoint_indices2);
narf_descriptor.getParameters ().support_size = support_size;
narf_descriptor.getParameters ().rotation_invariant = rotation_invariant;
pcl::PointCloud<pcl::Narf36> narf_descriptors;
narf_descriptor.compute (narf_descriptors);
cout << "Extracted "<<narf_descriptors.size ()<<" descriptors for "
<<keypoint_indices.points.size ()<< " keypoints.\n";
cout << narf_descriptors << endl;
这段代码实现了NARF描述子的计算,它首先创建了 NarfDescriptor 对象,并给了此对象输入数据(特征点索引和深度图像)。然后设置了两个重要的参数,support_size 确定了计算描述子时考虑的区域大小,在此区域内的点用来估算查询关键点的描述子,如果设置旋转不变(围绕法线旋转),则应该使用旋转不变的NARF描述子的版本。然后我们创建Narf36的点类型输出点云对象并进行实际计算。最后,打印输出特征点的数目和提取的描述子的数目。这两个数目有可能不同,一方面,特征点的描述子的估算可能失败,因为深度图像中有可能没有足够多的点(分辨率太低)进行计算某些特征点的描述子,或者在同一地方可能会有多个描述子,但是针对不同的主旋转(dominant rotations),生成的点云类型是Narf36类型(见common/include/pcl/point_types.h),是由36个浮点数元组成的描述子,以及x、y、z、roll、pitch、yaw来描述局部坐标系,在此坐标系中计算相应的特征值。后续就可以基于描述子进行比较分析做相应的配准识别等应用处理,例如:使用 Manhattan 距离(绝对误差和)进行对比等。剩余的代码只是在 range image widget 和3D viewer中对深度图像和特征点位置进行可视化。
【编译和运行程序】
在工作空间根目录narf_feature_extraction下,编写CMakeLists.txt文件如下:
cmake_minimum_required(VERSION 2.6 FATAL_ERROR)
project(narf_feature_extraction)
find_package(PCL 1.3 REQUIRED)
include_directories(${PCL_INCLUDE_DIRS})
link_directories(${PCL_LIBRARY_DIRS})
add_definitions(${PCL_DEFINITIONS})
add_executable (${PROJECT_NAME}_node src/narf_feature_extraction.cpp)
target_link_libraries (${PROJECT_NAME}_node ${PCL_LIBRARIES})
在工作空间根目录narf_feature_extraction下创建一个build文件夹,用于存放编译过程中产生的文件,然后执行编译:
mkdir build
cd build
cmake ..
make
此时,会在build文件夹下生成一个可执行文件narf_feature_extraction_node,运行该可执行文件:
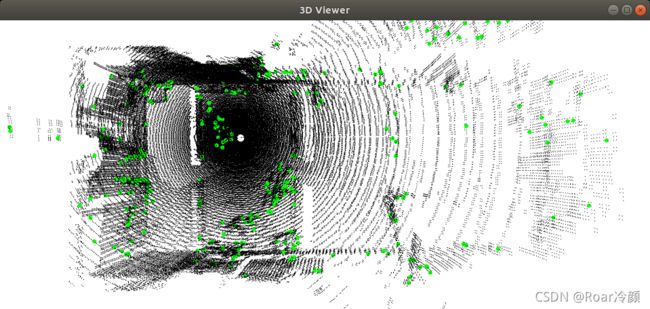
./narf_feature_extraction_node -m
运行上述命令后,如下图将自动生成一个呈矩形的点云,检测的特征点处在角落处。参数-m是必要的,因为矩形周围的区域观测不到,但属于边界部分,因此系统无法检测到这部分区域的特征点,选项-m将看不到的区域改变到最大范围读数,从而使系统能够使用这些边界区域。
也可以加载一个现有的点云文件来进行测试,把原始点云文件放置在build目录下,运行如下命令:
./narf_feature_extraction_node room_scan1.pcd
输出结果如下图所示,在三维视窗和二维深度图像视窗中,特征点以不同的显示方式凸显出来,可以直观地看到特征点地位置分布在空间物体地边缘处或空间变化明显地区域。
2 RoPs特征
RoPS为Rotational Projection Statistics 的简写,即旋转投影统计特征。RoPS特征具有对点云旋转和平移(即姿态变化)的不变性,具备很强的鉴别力以及对噪声和数据分辨率变化等干扰的良好稳健性。该特征目前已成功应用于三维目标识别、三维模型重建以及三维人脸识别等场景,均获得了优异的性能。此外,在多个数据集下的测试结果表明,其性能优于多个现有特征。
本节将首先分析RoPS特征描述算法的理论基础进而给出在PCL中的应用实例。RoPs特征理论基础及实验分析详见参考文献,PCL实例部分参考了PCL官网说明文档。
2.1 理论基础
2.1.1 生物视觉认知学启示
生物视觉认知学的相关实验研究结果表明,幼儿对三维物体的识别能力与其观察物体的角度数密切相关。若幼儿从多个角度观察物体,则其识别物体的能力将大大提高。此外,幼儿把持及观察物体的方式在很大程度上影响其识别物体的能力。研究结果认为,实现三维物体在人脑中的统一表示需要对来自物体多个视点的信息进行融合,而该融合则依赖于物体主轴所确定的参考框架。因此,幼儿如何旋转观察物体对信息融合的效果具有十分关键的作用。
上述认知学实验结果启示我们,在构建特征描述子时,若能将从多个视点获得的物体表面信息进行融合,将有助于提高特征描述子的鉴别力。此外,在生成特征描述子时,亦可依据物体的表面信息构建一个参考坐标框架,从而获得特征描述子对物体旋转和平移的不变性。
受此启发,提出了RoPS特征提取算法。该RoPS算法包含两个部分,即局部参考坐标框架构建和RoPS特征描述,详见下文叙述。
2.1.2 局部参考坐标框架构建
如下图所示,给定一个关键点 p p p 和支撑半径 r r r, 首先得到离关键点 p p p 的距离小于 r r r的局部表面 S S S,该局部表面包含 N N N 个三角形和 M M M 个顶点。对于第 i i i 个三角形,假设其顶点为 p i 1 p_{i1} pi1, p i 1 p_{i1} pi1 和 p i 1 p_{i1} pi1,则三角形中的任意一个点均可表示为:
p i ( s , t ) = p i 1 + s ( p i 2 − p i 1 ) + t ( p i 3 − p i 1 ) (1) p_{i}\left ( s,t \right ) = p_{i1} + s\left ( p_{i2}-p_{i1} \right ) + t\left ( p_{i3}-p_{i1} \right ) \tag{1} pi(s,t)=pi1+s(pi2−pi1)+t(pi3−pi1)(1)
其中, 0 ⩽ s , t ⩽ 1 , s + t ⩽ 1 0\leqslant s, t \leqslant 1, s+t\leqslant 1 0⩽s,t⩽1,s+t⩽1
则第 i i i 个三角形上点的散布矩阵 C i C_{i} Ci 可计算为:
C i = 1 12 ∑ j = 1 3 ∑ k = 1 3 ( p i j − p ) ( p i k − p ) T + 1 12 ∑ j = 1 3 ( p i j − p ) ( p i j − p ) T (2) C_{i} = \frac{1}{12}\sum_{j=1}^{3}\sum_{k=1}^{3} \left ( p_{ij}- p \right ) \left ( p_{ik}- p \right )^{T} + \frac{1}{12}\sum_{j=1}^{3} \left ( p_{ij}- p \right ) \left ( p_{ij}- p \right )^{T} \tag{2} Ci=121j=1∑3k=1∑3(pij−p)(pik−p)T+121j=1∑3(pij−p)(pij−p)T(2)
那么,局部表面 S S S 上所有点的总散布矩阵 C C C 可以计算为所有三角形散布矩阵的加权和,即:
C = ∑ i = 1 N w i 1 w i 2 C i (3) C = \sum_{i=1}^{N} w_{i1}w_{i2} C_{i} \tag{3} C=i=1∑Nwi1wi2Ci(3)
其中, w i 1 w_{i1} wi1 是第 i i i 个三角形的面积与局部表面 S S S 总面积的比值:
w i 1 = ∣ ( p i 2 − p i 1 ) × ( p i 3 − p i 1 ) ∣ ∑ i = 1 N ∣ ( p i 2 − p i 1 ) × ( p i 3 − p i 1 ) ∣ (4) w_{i1} = \frac{\left | \left ( p_{i2}-p_{i1} \right ) \times \left ( p_{i3}-p_{i1} \right ) \right |}{\sum_{i=1}^{N} \left | \left ( p_{i2}-p_{i1} \right ) \times \left ( p_{i3}-p_{i1} \right ) \right |} \tag{4} wi1=∑i=1N∣(pi2−pi1)×(pi3−pi1)∣∣(pi2−pi1)×(pi3−pi1)∣(4)
w i 2 w_{i2} wi2 是与关键点到第 i i i 个三角形中心距离相关的权值:
w i 2 = ( r − ∣ p − p i 1 + p i 2 + p i 3 3 ∣ ) 2 (5) w_{i2}= \left ( r - \left | p - \frac{p_{i1} + p_{i2} + p_{i3}}{3} \right | \right )^{2} \tag{5} wi2=(r−∣∣∣∣p−3pi1+pi2+pi3∣∣∣∣)2(5)
对该总散布矩阵 C C C 进行特征值分解,即:
C V = E V (6) CV = EV \tag{6} CV=EV(6)
其中, E E E 是由 C C C 的降序排列的特征值 { λ 1 , λ 2 , λ 3 } \left \{ \lambda _{1}, \lambda _{2}, \lambda _{3} \right \} {λ1,λ2,λ3} 构成的对角矩阵, V V V 包含了对应的特征向量 { v 1 , v 2 , v 3 } \left \{ v _{1},v _{2}, v _{3} \right \} {v1,v2,v3}。这三个相互正交的特征向量构成了局部参考坐标框架的基础。然而,这些特征向量的方向是随机的,因此目前得到的局部参考坐标框架不具有良好的可重复提取性。
为消除局部参考坐标框架坐标轴方向的二义性,将每个特征向量指向多数散布向量所指向的方向,因此特征向量与散布向量的内积符号可用于定义特征向量的不模糊方向。具体而言,不模糊特征向量 v ~ 1 \tilde{v}_{1} v~1 定义为:
v ~ 1 = v 1 ⋅ s i g n ( ∑ i = 1 N w i 1 w i 2 ( 1 6 ∑ j = 1 3 ( p i j − p ) v 1 ) ) (7) \tilde{v}_{1} = v_{1}\cdot sign\left ( \sum_{i=1}^{N} w_{i1}w_{i2}\left ( \frac{1}{6} \sum_{j=1}^{3}\left ( p_{ij}-p \right ) v_{1} \right ) \right ) \tag{7} v~1=v1⋅sign(i=1∑Nwi1wi2(61j=1∑3(pij−p)v1))(7)
其中 s i g n ( ⋅ ) sign(·) sign(⋅) 为符号函数。类似的,不模糊特征向量 v ~ 3 \tilde{v}_{3} v~3 可计算为:
v ~ 3 = v 3 ⋅ s i g n ( ∑ i = 1 N w i 1 w i 2 ( 1 6 ∑ j = 1 3 ( p i j − p ) v 3 ) ) (8) \tilde{v}_{3} = v_{3}\cdot sign\left ( \sum_{i=1}^{N} w_{i1}w_{i2}\left ( \frac{1}{6} \sum_{j=1}^{3}\left ( p_{ij}-p \right ) v_{3} \right ) \right ) \tag{8} v~3=v3⋅sign(i=1∑Nwi1wi2(61j=1∑3(pij−p)v3))(8)
给定两个不模糊向量 v ~ 1 \tilde{v}_{1} v~1 和 v ~ 3 \tilde{v}_{3} v~3 ,向量 v ~ 2 \tilde{v}_{2} v~2 定义为 v ~ 3 × v ~ 1 \tilde{v}_{3} \times \tilde{v}_{1} v~3×v~1。由此,得到了关键点 p p p 的不模糊局部参考坐标框架。在该框架中,原点为关键点 p p p ,三个坐标轴分别为 v ~ 1 \tilde{v}_{1} v~1 、 v ~ 2 \tilde{v}_{2} v~2 和 v ~ 3 \tilde{v}_{3} v~3。采用该局部参考坐标框架,从而可获得一个对姿态变化具有不变性的局部特征描述子。
2.1.3 RoPS特征描述
RoPS特征描述子的生成过程如下图所示。对于一幅输入点云或其Mesh表示(如下图(a)所示),首先获得每个关键点 p p p 上对应于支撑半径 r r r 的局部表面(如下图(b)所示),进而计算点 p p p 上的局部参考坐标框架。局部表面 S S S 上的三角形顶点可构成点云 Q = { q 1 , q 2 , . . . , q M } Q = \left \{ q_{1}, q_{2},...,q_{M} \right \} Q={q1,q2,...,qM} ,将该点云变换到局部参考坐标框架下以获得局部特征描述子对物体姿态变化的旋转和平移不变性。变换后的点云记为 Q ′ = { q 1 ′ , q 2 ′ , . . . , q M ′ } Q^{'} = \left \{ q^{'}_{1}, q^{'}_{2},...,q^{'}_{M} \right \} Q′={q1′,q2′,...,qM′}。

RoPS特征描述子的具体提取步骤如下:
(1)将点云 Q ′ Q^{'} Q′ 绕 x x x 轴旋转角度 θ k \theta _{k} θk,得到旋转后的点云 Q ′ ( θ k ) Q^{'}\left ( \theta _{k} \right ) Q′(θk),如上图 ( c ) (c) (c)所示。进而将点云 Q ′ ( θ k ) Q^{'}\left ( \theta _{k} \right ) Q′(θk) 投影到 x y xy xy、 x z xz xz 和 y z yz yz 三个坐标平面上以获得投影点云 Q ~ i ′ ( θ k ) , i = 1 , 2 , 3 \tilde{Q}^{'}_{i} \left ( \theta _{k} \right ) , i = 1,2,3 Q~i′(θk),i=1,2,3 。由于二维投影较好地保留了局部表面在该视角下的几何形状信息,对点云进行投影可实现三维局部表面的简洁高效描述。
(2)对于投影点云 Q ~ i ′ ( θ k ) \tilde{Q}^{'}_{i} \left ( \theta _{k} \right ) Q~i′(θk),将其二维包围框均匀划分成 L × L L \times L L×L 个单元格(如上图(d)所示),并统计落入每个单元格内的投影点数量,从而获得一个 L × L L \times L L×L 的分布矩阵 D D D(如上图(e)所示)。将分布矩阵 D D D 归一化以使得所有单元格中的数值之和为1,从而获得对数据分辨率变化的不变性。
(3)提取分布矩阵 D D D 的中心矩和香农熵。分布矩阵 D D D 的 m + n m+n m+n 阶中心矩 μ m n \mu _{mn} μmn 定义为:
μ m n = ∑ i = 1 L ∑ j = 1 L ( i − i ˉ ) m ( j − j ˉ ) n D ( i , j ) (9) \mu _{mn}= \sum_{i=1}^{L} \sum_{j=1}^{L} \left ( i-\bar{i} \right )^{m} \left ( j-\bar{j} \right )^{n} D\left ( i,j \right ) \tag{9} μmn=i=1∑Lj=1∑L(i−iˉ)m(j−jˉ)nD(i,j)(9)
分布矩阵 D D D 的香农熵 e e e 定义为:
e = − ∑ i = 1 L ∑ j = 1 L D ( i , j ) l o g ( D ( i , j ) ) (10) e= - \sum_{i=1}^{L} \sum_{j=1}^{L} D\left ( i,j \right ) log\left ( D\left ( i,j \right ) \right ) \tag{10} e=−i=1∑Lj=1∑LD(i,j)log(D(i,j))(10)
将这些中心矩与香农熵组合起来以得到一个统计向量,如上图(f)所示。进一步将 x y xy xy、 x z xz xz 和 y z yz yz 平面上的三个统计向量组合起来以得到子特征 f x ( θ k ) f_{x}\left ( \theta _{k} \right ) fx(θk)。该子特征 f x ( θ k ) f_{x}\left ( \theta _{k} \right ) fx(θk) 代表了点云绕 x x x 轴的第 k k k 次旋转所得到的统计量,如上图(g)所示。
(4)为全面记录局部表面的信息,将点云 Q ′ Q^{'} Q′ 绕 x x x 轴旋转一系列角度 { θ k } , k = 1 , 2 , … , T \left \{ \theta _{k} \right \}, k=1,2,…,T {θk},k=1,2,…,T,从而得到一系列子特征 { f x ( θ k ) } , k = 1 , 2 , … , T \left \{ f_{x}\left ( \theta _{k} \right ) \right \}, k=1,2,…,T {fx(θk)},k=1,2,…,T。然后,将点云 Q ′ Q^{'} Q′ 绕 y y y 轴旋转一系列角度以得到一系列子特征 { f y ( θ k ) } , k = 1 , 2 , … , T \left \{ f_{y}\left ( \theta _{k} \right ) \right \}, k=1,2,…,T {fy(θk)},k=1,2,…,T。最后,将点云 Q ′ Q^{'} Q′ 绕 z z z 轴旋转一系列角度以得到一系列子特征 { f z ( θ k ) } , k = 1 , 2 , … , T \left \{ f_{z}\left ( \theta _{k} \right ) \right \}, k=1,2,…,T {fz(θk)},k=1,2,…,T。
(5)将所有子特征连接起来便得到最终的RoPS特征描述子,即:
f = { { f x ( θ k ) } , { f y ( θ k ) } , { f z ( θ k ) } } , k = 1 , 2 , . . . , T (11) f = \left \{ \left \{ f_{x}\left ( \theta _{k} \right ) \right \},\left \{ f_{y}\left ( \theta _{k} \right ) \right \}, \left \{ f_{z}\left ( \theta _{k} \right ) \right \} \right \}, k = 1,2,..., T \tag{11} f={{fx(θk)},{fy(θk)},{fz(θk)}},k=1,2,...,T(11)
由于RoPS特征描述子从多个角度记录了局部表面的几何信息,因此其拥有很高的鉴别力。事实上,RoPS特征提取算法与生物认知学机理存在许多相通之处。首先,RoPS算法中将关键点支撑域内的邻域点绕三个坐标轴进行旋转并投影到三个坐标平面以得到一系列投影点分布矩阵的过程,类似于人眼从多个视点对三维物体进行二维成像的过程。其次,该算法采用少量统计矩记录每个投影点云分布矩阵信息的过程则类似人脑对图像信息的抽象理解过程。最后,该算法将所有统计矩信息连接得RoPS特征描述子的过程类似人脑对多视图像信息的融合理解及记忆过程。
2.1.4 推荐算法参数及说明
实验表明,如下参数能取得很好的性能:包围矩形划分单元格数 L L L 取为5,绕每个坐标轴的旋转次数 T T T 取为3,每个分布矩阵 D D D 采用向量 { μ 11 , μ 12 , μ 21 , μ 22 , e } \left \{ \mu _{11},\mu _{12},\mu _{21},\mu _{22}, e \right \} {μ11,μ12,μ21,μ22,e} 描述。
需要注意的是,上述中只给出了mesh数据格式(包含点和面元信息)下计算关键点 p p p处局部参考坐标框架的方法。若数据为点云表示(没有面元信息),则有两种解决方案。一是首先将点云采用三角化算法转化为mesh数据格式,然后采用上述方法计算局部参考坐标框架和RoPS特征描述子;二是采用其他算法(如SHOT)中的局部参考坐标框架模块计算局部参考坐标框架,而后在该局部参考坐标框架的基础上计算RoPS特征描述。
2.2 PCL应用实例详解
下文具体给出采用PCL计算点云RoPS特征的程序实例,源码是在PCL官方提供的源码基础上添加了对直方图可视化。
首先创建一个工作空间rops_feature,然后再在工作空间创建一个文件夹src用于存放源代码:
mkdir -p rops_feature/src
接着,在rops_feature/src路径下,创建一个文件并命名为rops_feature.cpp,拷贝如下代码:
#include &cloud,
const std::string &field_name,
const int index,
const std::string &id, int win_width, int win_height),但本例中的pcl::Histogram <135>是没用POINT_CLOUD_REGISTER_POINT_STRUCT注册过,即没有field_name,简单的显示方式就是把想显示
的点对应的特征向量,作为单独一个新的点云来对待,就可以显示*/
plotter->spin();
return (0);
}
【解释说明】
首先加载点云到cloud对象:
pcl::PointCloud<pcl::PointXYZ>::Ptr cloud (new pcl::PointCloud<pcl::PointXYZ> ());
if (pcl::io::loadPCDFile (argv[1], *cloud) == -1)
{
return (-1);
}
加载点云中需要计算RoPS特征的关键点的标号 indices。若对点云中的每一个点均需要计算RoPS特征,则可以将以下代码注释:
pcl::PointIndicesPtr indices = boost::shared_ptr <pcl::PointIndices> (new pcl::PointIndices ());
std::ifstream indices_file;
indices_file.open (argv[2], std::ifstream::in);
for (std::string line; std::getline (indices_file, line);)
{
std::istringstream in (line);
unsigned int index = 0;
in >> index;
indices->indices.push_back (index - 1);
}
indices_file.close ();
加载Mesh的面元信息 triangles 。若输入的为纯点云(没有面元信息)而非Mesh,则将下述代码替换为三角化( triangulation )程序。这里注意,该rops算法并非针对点云数据,而需求点之间拓扑信息,所以读者在使用中必须要有三角化这一步骤。
std::vector <pcl::Vertices> triangles;
std::ifstream triangles_file;
triangles_file.open (argv[3], std::ifstream::in);
for (std::string line; std::getline (triangles_file, line);)
{
pcl::Vertices triangle;
std::istringstream in (line);
unsigned int vertex = 0;
in >> vertex;
triangle.vertices.push_back (vertex - 1);
in >> vertex;
triangle.vertices.push_back (vertex - 1);
in >> vertex;
triangle.vertices.push_back (vertex - 1);
triangles.push_back (triangle);
}
设置用于RoPS特征提取的参数:设置局部邻域大小的支撑半径 support _radius,该数值越大,包含的表面信息越多,但同时受遮挡和背景干扰的影响也越大。极端的情况,若该支撑半径能将一个场景的所有点云均包含进去,则提取到的特征为全局特征。推荐设置为点云分辨率的15倍;设置获得分布矩阵的投影平面划分单元格数 number_of_partition_bins,推荐设置为5;设置绕每个坐标轴的旋转次数 number_of_rotations ,推荐设置为3。
float support_radius = 0.0285f;
unsigned int number_of_partition_bins = 5;
unsigned int number_of_rotations = 3;
设置特征提取算法中使用到的邻域点搜索函数,如k-d树:
pcl::search::KdTree<pcl::PointXYZ>::Ptr search_method (new pcl::search::KdTree<pcl::PointXYZ>);
search_method->setInputCloud (cloud);
实例化pcl::ROPSEstimation类:
pcl::ROPSEstimation <pcl::PointXYZ, pcl::Histogram <135> > feature_estimator;
feature_estimator.setSearchMethod (search_method);
feature_estimator.setSearchSurface (cloud);
feature_estimator.setInputCloud (cloud);
feature_estimator.setIndices (indices);
feature_estimator.setTriangles (triangles);
feature_estimator.setRadiusSearch (support_radius);
feature_estimator.setNumberOfPartitionBins (number_of_partition_bins);
feature_estimator.setNumberOfRotations (number_of_rotations);
feature_estimator.setSupportRadius (support_radius);
计算RoPS特征:
pcl::PointCloud<pcl::Histogram <135> >::Ptr histograms (new pcl::PointCloud <pcl::Histogram <135> > ());
feature_estimator.compute (*histograms);
【编译和运行程序】
在工作空间根目录rops_feature下,编写CMakeLists.txt文件如下:
cmake_minimum_required(VERSION 2.8 FATAL_ERROR)
project(rops_feature)
find_package(PCL 1.8 REQUIRED)
include_directories(${PCL_INCLUDE_DIRS})
link_directories(${PCL_LIBRARY_DIRS})
add_definitions(${PCL_DEFINITIONS})
add_executable (${PROJECT_NAME}_node src/rops_feature.cpp)
target_link_libraries (${PROJECT_NAME}_node ${PCL_LIBRARIES})
在工作空间根目录rops_feature下创建一个build文件夹,用于存放编译过程中产生的文件,然后执行编译:
mkdir build
cd build
cmake ..
make
此时,会在build文件夹下生成一个可执行文件rops_feature_node,然后把points.pcd、indices.txt和triangles.txt三个文件放入到build文件夹,最后运行该可执行文件:
./rops_feature_node points.pcd indices.txt triangles.txt
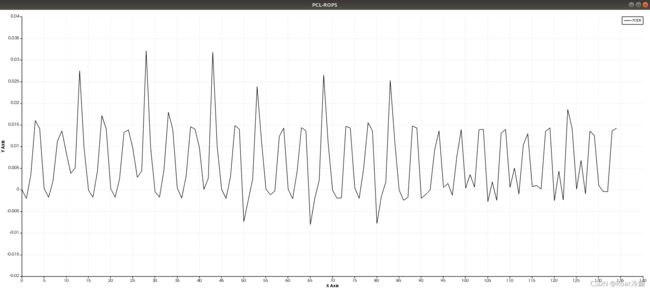
运行上述命令后,可视化结果如下所示:
3 基于惯性矩与偏心率的描述子
本小节我们将学习如何利用 pcl:: MomentOflnertiaEstimation 类获取基于惯性矩(moment of inertia )与偏心率( eccentricity )的描述子,该类的另一功能是提取有向包围盒OBB(Oriented Bounding Box )和坐标轴对齐包围盒AABB(Axis-Aligned Bounding Box )。但是请读者注意,所提取的有向包围盒OBB并不一定是最小的包围盒,这里提到的包围盒常用于物理模拟或可视化中用到的碰撞检测等。
3.1 理论基础
该特征提取的核心思想如下:首先计算点云的协方差矩阵,然后提取特征值和特征向量,并且构造局部坐标系,以点云重心为坐标系原点,得到的特征向量已被归一化,并且以主特征向量( Major Eigen Vector )作为X轴,最小特征值对应的特征向量(Minor Eigen Vector )作为Z轴,剩下的特征向量作为Y轴,符合右手坐标系原则。接下来进行迭代计算,每一次迭代,主特征向量即X轴按照顺序绕其他两个轴(YZ轴)旋转,实现当中具体是外循环绕Y轴0到90度,内循环绕Z轴0到360度,每次添加一定的角度(用step_变量控制),最终的X轴正方向遍历了整个Z轴负方向的半球离散方向,我们将这个旋转主向量X轴作为当前轴。对于每个当前轴,计算一个惯性矩。另外,利用当前轴也可以计算一个偏心率,具体是将当前轴正向即旋转后的X轴正向视为假设平面的法向量,然后将输入点云投影到该假设平面上。接下来,根据获取的投影就可以构造一个偏心率,其中长轴和短轴的数值是通过投影后点云的协方差矩阵得到。这样就在每个当前轴上得到一个惯性矩和一个偏心率,迭代完成后得到两个向量来存储惯性矩和偏心率作为特征。类pcl: MomentOfInertiaEstimation不仅提供了对上述特征的获取过程,并且可以输出AABB(与坐标系本身的轴向对应),以及OBB,其中OBB就是局部坐标系对应的AABB。
3.2 源代码解析
首先创建一个工作空间MomentOfInertiaEstimation,然后再在工作空间创建一个文件夹src用于存放源代码:
mkdir -p MomentOfInertiaEstimation/src
接着,在MomentOfInertiaEstimation/src路径下,创建一个文件并命名为moment_of_inertia.cpp,拷贝如下代码:
#include 【解释说明】
下面对上述源代码中的关键语句进行解析。
pcl::MomentOfInertiaEstimation <pcl::PointXYZ> feature_extractor;
feature_extractor.setInputCloud (cloud);
feature_extractor.compute ();
对 pcl::MomentOfInertiaEstimation 进行实例化,然后,设置输入点云,并开始特征计算。
std::vector <float> moment_of_inertia; // 存储惯性矩阵的特征向量
std::vector <float> eccentricity; // 存储偏心率的特征向量
pcl::PointXYZ min_point_AABB;
pcl::PointXYZ max_point_AABB;
pcl::PointXYZ min_point_OBB;
pcl::PointXYZ max_point_OBB;
pcl::PointXYZ position_OBB;
Eigen::Matrix3f rotational_matrix_OBB;
float major_value, middle_value, minor_value;
Eigen::Vector3f major_vector, middle_vector, minor_vector;
Eigen::Vector3f mass_center;
以上几行代码用于声明所有必要的变量,这些变量用于存储特征向量和描述包围盒的几何位置方向等。
feature_extractor.getMomentOfInertia (moment_of_inertia); // 获取惯性矩特征
feature_extractor.getEccentricity (eccentricity); // 获取偏心率特征
feature_extractor.getAABB (min_point_AABB, max_point_AABB); // 获取AABB对应的左下角和右上角坐标
feature_extractor.getOBB (min_point_OBB, max_point_OBB, position_OBB, rotational_matrix_OBB); // 获取OBB对应的相关参数
feature_extractor.getEigenValues (major_value, middle_value, minor_value); // 求解三个特征值
feature_extractor.getEigenVectors (major_vector, middle_vector, minor_vector); // 求解三个特征向量
feature_extractor.getMassCenter (mass_center); // 求解点云中心坐标
以上代码用于获取计算所得的特征向量和其他相关参数,后续代码用于可视化OBB和AABB。
【编译和运行程序】
在工作空间根目录MomentOfInertiaEstimation下,编写CMakeLists.txt文件如下:
cmake_minimum_required(VERSION 2.8 FATAL_ERROR)
project(moment_of_inertia)
find_package(PCL 1.8 REQUIRED)
include_directories(${PCL_INCLUDE_DIRS})
link_directories(${PCL_LIBRARY_DIRS})
add_definitions(${PCL_DEFINITIONS})
add_executable (${PROJECT_NAME}_node src/moment_of_inertia.cpp)
target_link_libraries (${PROJECT_NAME}_node ${PCL_LIBRARIES})
在工作空间根目录MomentOfInertiaEstimation下创建一个build文件夹,用于存放编译过程中产生的文件,然后执行编译:
mkdir build
cd build
cmake ..
make
此时,会在build文件夹下生成一个可执行文件moment_of_inertia_node,运行该可执行文件:
./moment_of_inertia_node lamppost.pcd
运行上述命令后,有向包围盒OBB,轴对齐包围盒AABB,和特征向量的可视化结果如下图所示。绿色的包围盒为OBB,红色的包围盒为AABB,从图中可以看出,输入点云的OBB其实就是以构造的局部坐标系对应的AABB,而输入点云的AABB与全局坐标系对应。
4 BoundaryEstimation 进行边界提取
边界数据属于一种常用的特征数据,本小节将学习如何求一个输入点云数据的边界点云,利用pcl中提供的 pcl :: BoundaryEstimation类完成。
首先创建一个工作空间boundary,然后再在工作空间创建一个文件夹src用于存放源代码:
mkdir -p boundary/src
接着,在boundary/src路径下,创建一个文件并命名为boundary.cpp,拷贝如下代码:
#include 【解释说明】
下面解析上述源代码的关键语句。我们先声明了 BoundaryEstimation 结构和 NormalEstimation 等类对应的头文件:
#include 随后我们在边界估计的函数中创建定义了存储边界估计结果的对象 boundaries,进行边界特征估计的对象 boundEst ,以及法线估计对象 normEst。 这里有多个参数需要用户根据自己的数据进行调整,其中影响主要是估计法线的半径设置 normEst.setRadiusSearch(reforn)。设置为分辨率的10倍时,效果较好,主要是对于法线估计。邻域半径选择太小了,噪声较大,估计的法线就容易出现错误,而搜索邻域半径设置太大估计速度就比较慢。boundEst.setRadiusSearch(re),也设置10倍,太小则内部的很多点就都当成边界点了。最后一个参数是边界判断时的角度阈值,默认值为PI/2,此处设置为PI/4,用户也可以根据需要进行更改。
pcl::PointCloud<pcl::Boundary> boundaries;
pcl::BoundaryEstimation<pcl::PointXYZ, pcl::Normal, pcl::Boundary> boundEst;
pcl::NormalEstimation<pcl::PointXYZ, pcl::Normal> normEst;
pcl::PointCloud<pcl::Normal>::Ptr normals(new pcl::PointCloud<pcl::Normal>);
pcl::PointCloud<pcl::PointXYZ>::Ptr cloud_boundary (new pcl::PointCloud<pcl::PointXYZ>); // 存储最终判断为边界点的点云对象
normEst.setInputCloud(pcl::PointCloud<pcl::PointXYZ>::Ptr(cloud));
normEst.setRadiusSearch(reforn);
normEst.compute(*normals); // 估计法线
boundEst.setInputCloud(cloud);
boundEst.setInputNormals(normals);
boundEst.setRadiusSearch(re);
boundEst.setAngleThreshold(M_PI/4);
boundEst.setSearchMethod(pcl::search::KdTree<pcl::PointXYZ>::Ptr (new pcl::search::KdTree<pcl::PointXYZ>));
boundEst.compute(boundaries); // 估计边界
/* 存储估计为边界的点云数据 */
for(int i = 0; i < cloud->points.size(); i++)
{
if(boundaries[i].boundary_point > 0)
{
cloud_boundary->push_back(cloud->points[i]);
}
}
类 BoundaryEstimation 的输出为 pcl::PointCloud,从pcl内部源码分析可以知道,返回的值赋给 pcl::Boundary 是bool型,也就是 pcl::Boundary 等于0时,表示判断为非边界,而大于0时为边界。这样我们就用一个for循环,将所有边界点,存储在另一个点云对象中,方便可视化。
下面是对原始点云和估计结果进行可视化的代码,此处不再细讲。可视化的主要目的是为了用户根据自己的数据调整上述的参数。
/* 创建含有两个视口的可视化对象,分别将原始点云和估计的边界点云进行可视化 */
boost::shared_ptr<pcl::visualization::PCLVisualizer> MView (new pcl::visualization::PCLVisualizer ("BoundaryEstimation"));
int v1(0);
MView->createViewPort (0.0, 0.0, 0.5, 1.0, v1);
MView->setBackgroundColor (0.3, 0.3, 0.3, v1);
MView->addText ("Raw point clouds", 10, 10, "v1_text", v1);
int v2(0);
MView->createViewPort (0.5, 0.0, 1, 1.0, v2);
MView->setBackgroundColor (0.5, 0.5, 0.5, v2);
MView->addText ("Boudary point clouds", 10, 10, "v2_text", v2);
MView->addPointCloud<pcl::PointXYZ> (cloud, "sample cloud",v1);
MView->addPointCloud<pcl::PointXYZ> (cloud_boundary, "cloud_boundary",v2);
MView->setPointCloudRenderingProperties (pcl::visualization::PCL_VISUALIZER_COLOR, 1,0,0, "sample cloud",v1);
MView->setPointCloudRenderingProperties (pcl::visualization::PCL_VISUALIZER_COLOR, 0,1,0, "cloud_boundary",v2);
MView->addCoordinateSystem (1.0);
MView->initCameraParameters ();
MView->spin();
【编译和运行程序】
在工作空间根目录MomentOfInertiaEstimation下,编写CMakeLists.txt文件如下:
cmake_minimum_required(VERSION 2.8 FATAL_ERROR)
project(moment_of_inertia)
find_package(PCL 1.8 REQUIRED)
include_directories(${PCL_INCLUDE_DIRS})
link_directories(${PCL_LIBRARY_DIRS})
add_definitions(${PCL_DEFINITIONS})
add_executable (${PROJECT_NAME}_node src/moment_of_inertia.cpp)
target_link_libraries (${PROJECT_NAME}_node ${PCL_LIBRARIES})
在工作空间根目录boundary下创建一个build文件夹,用于存放编译过程中产生的文件,然后执行编译:
mkdir build
cd build
cmake ..
make
此时,会在build文件夹下生成一个可执行文件boundary_node,运行该可执行文件:
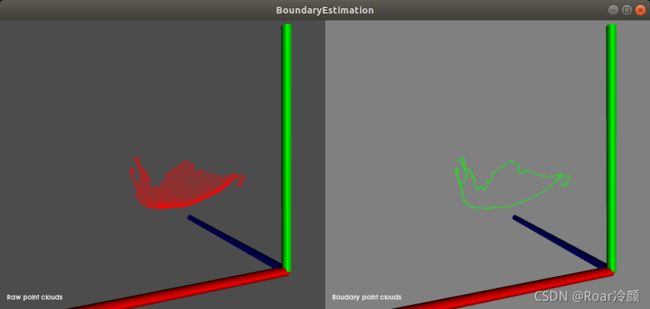
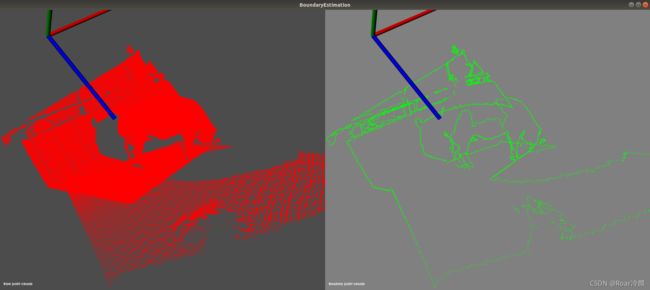
./boundary_node 1.pcd 0.05 0.05
会看到如下图所示类似的结果,命令行参数中,第一个为输入点云,第二个为估计法线的半径,第三个为边界估计时,搜索的邻域范围半径。博主测试了分割后对象的边界提取和整个场景的边界提取:对于分割后对象一般可以用来进一步计算和对象本身相关的信息;而整个场景的边界提取结果,就可以作为其他特征提取的输入,比如直线提取等,也可以作为配准数据时对应区域来对待,以提高配准速度。