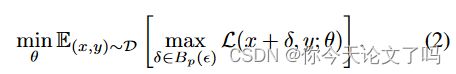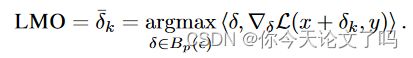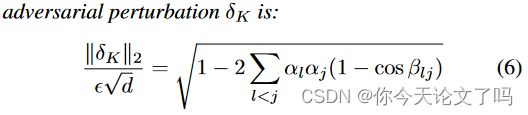Understanding and Increasing Efficiency of Frank-Wolfe Adversarial Training

AT存在灾难性的过拟合，在训练过程中对抗精度下降，尽管已经提出了改进，但它们增加了训练时间，鲁棒性与多步 AT 相去甚远。我们开发了一个使用 FW 优化 (FW-AT) 进行对抗训练的理论框架，揭示了损失情况与 ℓ∞ FW 攻击的 ℓ2 失真之间的几何联系。我们分析表明，FW 攻击的高失真相当于攻击路径上的小梯度变化。然后在各种深度神经网络架构上通过实验证明，针对鲁棒模型的 ℓ∞ 攻击实现了接近最大的失真，而标准网络具有较低的失真。实验表明，灾难性过拟合与 FW 攻击的低失真密切相关。这种数学透明度将 FW 与投影梯度下降 (PGD) 优化区分开来。为了证明我们的理论框架的实用性，我们开发了 FW-AT-Adapt，这是一种新颖的对抗性训练算法，它使用简单的失真度量来调整训练期间的攻击步骤数量，从而在不影响鲁棒性的情况下提高效率。 FW-AT-Adapt 提供与单步快速 AT 方法相当的训练时间，并缩小了快速 AT 方法和多步 PGD-AT 之间的差距，同时在白盒和黑盒设置中的对抗精度损失最小。

文章主要贡献：

•我们根据经验证明，针对鲁棒模型的FW攻击在各种网络架构中实现了接近最大的失真。
•我们的经验表明，即使只有2个步骤，FW攻击的失真也与灾难性过度拟合密切相关。
•推导出了将FW攻击的失真与攻击路径上的梯度变化相关的理论保证，这意味着通过几个步骤计算的高失真攻击会导致损失的增加。
•受失真和攻击路径梯度变化之间的联系启发，我们提出了一种自适应步长Frank Wolfe对抗性训练算法FW-AT-ADAPT，与单步AT相比，该算法实现了卓越的鲁棒性/训练时间权衡，并在针对强白盒和黑盒攻击进行评估时，弥补了此类方法与多步AT变体之间的差距。

Background and Previous Work

AT：训练分类器的流行方式是通过经验风险最小化ERM：

使用ERM原理（1）训练神经网络在测试集上提供了高精度，但使网络容易受到对抗性攻击。
最流行和有效的防御措施之一是对抗性训练（AT）[20]，它不使用ERM原则，而是将对抗性风险降至最低。

 为了在给定的输入x处构建对抗性攻击，这些防御使用投影梯度下降（PGD）来使用固定数量的步骤来近似受约束的内部最大化。PGD使用迭代更新计算对抗性扰动：

 该方法的计算成本主要取决于用于近似内部最大化的步骤数，因为K步PGD近似最大化涉及通过网络的K个正向反向传播。虽然使用较少的PGD步骤可以降低这一成本，但这些步骤会导致较弱的攻击，从而导致梯度混淆，这是一种现象，网络通过使损失场景高度非线性和不太鲁棒的模型来学习抵御基于梯度的攻击。许多防御已经被证明可以被新的攻击所规避，而对抗性训练已经被证明能够保持最先进的鲁棒性。这种性能仅通过半监督方法得到改善。

Frank Wolfe（FW）优化算法起源于凸优化，尽管最近已证明在更一般的设置中表现良。该方法首先优化原始问题的线性近似，称为线性最大化Oracle（LMO）

 

 我们提出了Frank Wolfe对抗训练（FW-AT），它用Frank Wolfe优化器代替PGD内部优化。FW-AT实现了与其PGD对应物类似的鲁棒性。使用FW攻击路径的封闭形式表达式，我们导出了攻击失真和沿攻击路径的损失梯度变化之间的几何关系。这一关键见解导致FW-AT的简单修改，其中每个时期的步长根据ℓ2攻击的失真，并且被证明可以减少训练时间，同时提供强大的鲁棒性而不会遭受灾难性的过度拟合。

许多快速AT方法依赖于单个梯度步长，这可能导致灾难性的过度拟合（CO），这是一种现象，即模型对多步攻击的性能收敛到一个较高的值，但随后突然下降。这表明该模型对单步训练攻击的权重过拟合

Multi-step High Distortion Attacks are Inefficient

我们分析FW攻击失真的主要工具，FW-AT在数学上比PGD-AT更透明的一个主要原因，是将FW攻击表示为LMO迭代的凸组合。我们将优化过程中采取的步骤称为攻击路径。

定理1： Higher distortion is equivalent to lower gradient variation throughout the attack path.（较高的失真相当于整个攻击路径的较低梯度变化。）

 

具体地说，攻击的每一步之间符号变化的累积减少了失真。在极度扭曲攻击的极端情况下，这意味着攻击位于ℓ∞ 在进攻路径上的任何一步之间，球的梯度符号可能没有变化。因此，每个步骤都是恒定的，攻击相当于FW（1）攻击或FGSM。这在图1中以图形方式进行了说明。进一步遵循这一逻辑，我们能够根据最终失真来量化不同阶跃攻击之间的距离。

定理2：Multi-step attacks with high distortion are inefficient.（具有高失真的多级攻击是低效的。） 

这表明，在FW-AT期间，使用大量步骤来近似对抗性风险，一旦达到攻击的高失真，就会导致回报减少，因为最后一步将接近早期步骤。另一个方向也是正确的：
受到低失真扰动攻击的模型可以从更多步骤的训练中受益 

Frank-Wolfe Adversarial Training Algorithm

算法2中提供了自适应弗兰克·沃尔夫对抗训练方法（FW-AT-ADAPT）的伪码。对PGD-AT进行了以下修改：

（i）使用FW优化方案（算法1）计算对抗攻击

（ii）对于每个历元的前Bm批，监测FW（2）攻击的失真。如果这些批次的平均失真高于阈值r，则攻击步骤K的数量在历元的剩余时间内降至K/2。或者，如果它低于r，则K增加2

 虽然深度神经网络中的损失函数L（fθ（x+δ），y）通常是非凸的，但我们做出以下假设

 

 界限（9）断言，在高失真设置中，由高阶FW攻击获得的梯度以及因此的权重更新接近于低阶FW进攻的梯度。因此，期望使用所提出的自适应算法实现类似水平的对抗鲁棒性。

Choosing the Target Distortion Ratio

推论1告诉我们，FW（2）的失真是x处和FGSM攻击时损失梯度的符号变化比数的函数。