计量经济学 学习笔记(长篇 未完成)
文章目录
- 前言
- 一、基本模型
-
- 1、一元线性回归模型
- 2、多元线性回归模型
- 3、可线性化的非线性模型
- 二、数据特征
-
- 1、处理异方差
- 2、自相关
- 3、多重共线性
- 4、虚拟变量的应用
- 5、F,LR,Wald,JB检验
- 三、面板数据类型
-
- 1、混合模型
- 2、固定效应模型
- 3、随机效应模型
- 四、其他
- 总结
前言
2021年暑假自学的内容,现由纸质笔记整理到CSDN上。
一、基本模型
1、一元线性回归模型
回归线的定义
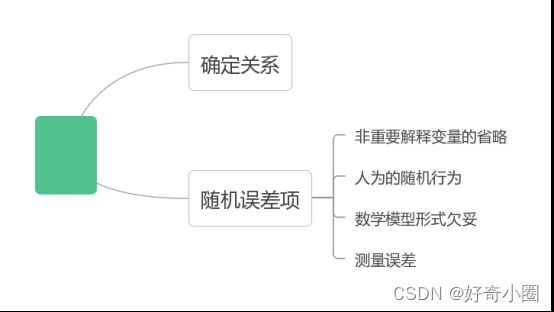
回归线的基本假定
关于模型关系的假设:模型设定正确假设、线性回归假设;
关于解释变量的假设:确定性假设、与随机项不相关假设、观测值变化假设、无完全共线性假设、样本方差假设(随着样本容量的无限增加。解释变量x的样本方差趋于一有限常数,时间序列);
关于随机项的假设:0均值假设
E ( μ i ∣ X i ) = 0 , i = 1 , 2 , ⋯ , n E\left(\mu_{i} \mid X_{i}\right)=0, i=1,2, \cdots, n E(μi∣Xi)=0,i=1,2,⋯,n
同方差假设
Var ( μ i ∣ X i ) = σ 2 , i = 1 , 2 , ⋯ , n \operatorname{Var}\left(\mu_{i} \mid X_{i}\right)=\sigma^{2}, i=1,2, \cdots, n Var(μi∣Xi)=σ2,i=1,2,⋯,n
序列不相关假设
Cov ( μ i , μ j ∣ X i , X j ) = 0 , i , j = 1 , 2 , ⋯ , n , i ≠ j \operatorname{Cov}\left(\mu_{i}, \mu_{j} \mid X_{i}, X_{j}\right)=0, i, j=1,2, \cdots, n, i \neq j Cov(μi,μj∣Xi,Xj)=0,i,j=1,2,⋯,n,i=j;
随机项的正态性假设:正态性假设
μ i ∼ N ( 0 , σ 2 ) → μ i ∼ NID ( 0 , σ 2 ) \mu_{i} \sim N\left(0, \sigma^{2}\right) \rightarrow \mu_{i} \sim \operatorname{NID}\left(0, \sigma^{2}\right) μi∼N(0,σ2)→μi∼NID(0,σ2)
平方和
y i ^ = Y i ^ − Y i ˉ \widehat{y_{i}}= \widehat{Y_{i}}- \bar{Y_{i}} yi =Yi −Yiˉ
∑ y i 2 = ∑ y i ^ 2 + ∑ u i ^ 2 \sum y_{i}^2=\sum \widehat{y_i}^2+\sum \widehat{u_i}^2 ∑yi2=∑yi 2+∑ui 2
u i ^ = U i ^ \widehat{u_i}=\widehat{U_i} ui =Ui
总平方和(波动程度)TSS:
∑ y i 2 \sum y_{i}^2 ∑yi2
解释平方和ESS:
∑ y i ^ 2 \sum \widehat{y_i}^2 ∑yi 2
残差平方和RSS( y i y_{i} yi的波动,没有被 x i x_{i} xi解释的部分):
∑ u i ^ 2 \sum \widehat{u_i}^2 ∑ui 2
拟合优度定义及含义
可决系数 R 2 R^2 R2:被解释变量的波动程度,由解释变量解释的那一部分
R 2 = E S S / T S S = 1 − R S S / T S S R^2=ESS/TSS=1-RSS/TSS R2=ESS/TSS=1−RSS/TSS
相关性r:常见的有斯皮尔曼相关性(不要求正态分布)、皮尔逊相关性(要求正态分布)
随机干扰项方差的置信区间
( n − 2 ) δ ^ 2 δ 2 \frac{(n-2) \widehat{\delta}^2}{ \delta ^2} δ2(n−2)δ 2服从卡方分布,其中 δ 2 \delta^2 δ2置信区间为 ( n − 2 ) δ ^ 2 x a / 2 2 , ( n − 2 ) δ ^ 2 x 1 − a / 2 2 ] \frac{(n-2)\widehat{\delta}^2}{x_{a/2}^2},\frac{(n-2)\widehat{\delta}^2}{x_{1-a/2}^2}] xa/22(n−2)δ 2,x1−a/22(n−2)δ 2]
假设检验略
均值预测和个体预测
个体预测: x 0 x_0 x0相对应 y y y的个别值,回归线上的值+随机误差项
均值预测:回归线上的点(用历史点预测)
对于方差:个体预测>均值预测
检验步骤:
(1)散点图(k个点)
(2)线性回归(得到方程和t统计量) R 2 、 S e 、 T R^2、Se、T R2、Se、T
(3)回归系数的显著性检验(设 H 0 H_0 H0、 H 1 H_1 H1,显著性水平为 x x x, t a 2 ( k ) t_{\frac{a}{2}}(k) t2a(k))为临界值,看t统计量是否超过该临界值,超过则拒绝原假设。
注意:y=ax+b,b是否通过显著性检验都不应该删去
2、多元线性回归模型
多元回归模型的矩阵表达形式
Y = [ y 1 y 2 ⋮ y n ] , X = [ 1 x 11 ⋯ x 1 p 1 x 21 ⋯ x 2 p ⋮ ⋮ ⋮ 1 x n 1 ⋯ x n p ] , ϵ = [ ϵ 1 ϵ 2 ⋮ ϵ n ] , β = [ β 0 β 1 ⋮ β p ] Y=\left[\begin{array}{c} y_{1} \\ y_{2} \\ \vdots \\ y_{n} \end{array}\right], X=\left[\begin{array}{cccc} 1 & x_{11} & \cdots & x_{1 p} \\ 1 & x_{21} & \cdots & x_{2 p} \\ \vdots & \vdots & & \vdots \\ 1 & x_{n 1} & \cdots & x_{n p} \end{array}\right], \epsilon=\left[\begin{array}{c} \epsilon_{1} \\ \epsilon_{2} \\ \vdots \\ \epsilon_{n} \end{array}\right], \beta=\left[\begin{array}{c} \beta_{0} \\ \beta_{1} \\ \vdots \\ \beta_{p} \end{array}\right] Y=⎣⎢⎢⎢⎡y1y2⋮yn⎦⎥⎥⎥⎤,X=⎣⎢⎢⎢⎡11⋮1x11x21⋮xn1⋯⋯⋯x1px2p⋮xnp⎦⎥⎥⎥⎤,ϵ=⎣⎢⎢⎢⎡ϵ1ϵ2⋮ϵn⎦⎥⎥⎥⎤,β=⎣⎢⎢⎢⎡β0β1⋮βp⎦⎥⎥⎥⎤
Y = X ⋅ β + ϵ Y=X \cdot \beta+\epsilon Y=X⋅β+ϵ
最小二乘法(略)
可决系数
R ˉ 2 = 1 − R S S / ( N − k − 1 ) T S S / ( N − 1 ) = 1 − N − 1 N − k − 1 ⋅ T S S − E S S T S S \bar{R}^2=1-\frac{RSS/(N-k-1)}{TSS/(N-1)}=1-\frac{N-1}{N-k-1}\cdot\frac{TSS-ESS}{TSS} Rˉ2=1−TSS/(N−1)RSS/(N−k−1)=1−N−k−1N−1⋅TSSTSS−ESS
R ˉ 2 = 1 − N − 1 N − k − 1 ⋅ ( 1 − R 2 ) \bar{R}^2=1-\frac{N-1}{N-k-1}\cdot(1-R^2) Rˉ2=1−N−k−1N−1⋅(1−R2)
指标
回归均方MSE:解释平方和ESS除以自由度k,这里的k为解释变量的个数
误差均方MSR:残差平方和RSS除以自由度N-k-1
由上述可得:
F = M S R M S E = E S S / k R S S / N − k − 1 ∼ F ( k , N − k − 1 ) F=\frac{MSR}{MSE}=\frac{ESS/k}{RSS/N-k-1}\sim F(k,N-k-1) F=MSEMSR=RSS/N−k−1ESS/k∼F(k,N−k−1)
预测误差: e i = Y i ^ − Y i e_{i}=\widehat{Y_{i}}-Y_{i} ei=Yi −Yi
相对误差: P E = ( Y i ^ − Y i ) / Y i PE=(\widehat{Y_{i}}-Y_{i})/Y_{i} PE=(Yi −Yi)/Yi
误差均方根: R M S = 1 T ∑ ( Y i ^ − Y i ) 2 RMS=\sqrt{\frac{1}{T}\sum(\widehat{Y_{i}}-Y_{i})^2} RMS=T1∑(Yi −Yi)2
相对误差绝对值平均: M A P E = 1 T ∑ ∣ Y i ^ − Y i Y i ∣ MAPE=\frac{1}{T}\sum|\frac {\widehat{Y_{i}}-Y_{i}}{Y_{i}}| MAPE=T1∑∣YiYi −Yi∣
Theil不等系数(衡量预测值偏离实际发生值的程度):越接近0,误差越小
标准化
Y i − Y S ( Y i ) = β 1 ⋅ X i 1 − X 1 ˉ S ( X i 1 ) + β 2 ⋅ X i 2 − X 2 ˉ S ( X i 2 ) + u i \frac{Y_i-Y}{S(Y_i)}=\beta_1 \cdot \frac{X_{i1}-\bar{X_1}}{S(X_{i1})}+\beta_2 \cdot \frac{X_{i2}-\bar{X_2}}{S(X_{i2})}+u_i S(Yi)Yi−Y=β1⋅S(Xi1)Xi1−X1ˉ+β2⋅S(Xi2)Xi2−X2ˉ+ui
注意:回归模型的残差项中没有自相关和异方差,解释变量中没有多重共线性,而且解释变量应该满足外生性假定。稳定性要强,超样本特性要好。
步骤
1.散点图,判断能否线性回归
2.建立模型 Y t = β 0 + β 1 ⋅ x 1 t . . . + u t Y_t=\beta_0 + \beta_1 \cdot x_{1t}...+u_t Yt=β0+β1⋅x1t...+ut
3.数据处理得 β 0 , β 1 . . . . \beta_0,\beta_1.... β0,β1....、t统计量、 t a 2 ( k ) t_{\frac{a}{2}}(k) t2a(k)判断显著性,再利用可决系数 R 2 R^2 R2、自相关性DW等判断拟合优度
4.样本外预测(可一点):点估计、区间估计。样本内预测(稳健性判断)
3、可线性化的非线性模型
标准线性:对变量线性、对参数线性
多项式函数模型:倒数函数模型、对数函数模型、指数函数模型、幂函数函数模型、生长曲线函数模型
多项式函数模型
y = β 0 + β 1 ⋅ x i + β 2 ⋅ x i 2 + . . . + β k ⋅ x i k + u i y=\beta_0+\beta_1 \cdot x_i+\beta_2 \cdot x_i^2+...+\beta_k \cdot x_{i}^k+u_i y=β0+β1⋅xi+β2⋅xi2+...+βk⋅xik+ui
转为:
y = β 0 + β 1 ⋅ z 1 + β 2 ⋅ z 2 + . . . + β k ⋅ z k + u i y=\beta_0+\beta_1 \cdot z_1+\beta_2 \cdot z_2+...+\beta_k \cdot z_k+u_i y=β0+β1⋅z1+β2⋅z2+...+βk⋅zk+ui
常用的有二次、三次,二次:总成本函数模型。三次:边际成本函数模型、平均成本函数模型。
倒数、对数、指数、幂函数模型
倒数: y i = β 0 + β 1 / x i + u i y_i=\beta_0+\beta_1/x_i+u_i yi=β0+β1/xi+ui转为 y i = β 0 + β 1 ⋅ x i ∗ + u i y_i=\beta_0+\beta_1 \cdot x_{i}^{*}+u_i yi=β0+β1⋅xi∗+ui
对数: y i = β 0 + β 1 ⋅ L n ( x i ) + u i y_i=\beta_0+\beta_1 \cdot Ln(x_i)+u_i yi=β0+β1⋅Ln(xi)+ui转为 y i = β 0 + β 1 ⋅ x i ∗ + u i y_i=\beta_0+\beta_1 \cdot x_{i}^{*}+u_i yi=β0+β1⋅xi∗+ui
指数: y i = β 0 e β 1 ⋅ x i + u i y_i=\beta_0 e^{\beta_1 \cdot x_i+u_i} yi=β0eβ1⋅xi+ui转为 l n ( y i ) = l n ( β 0 ) + β 1 ⋅ ln(y_i)=ln(\beta_0)+\beta_1 \cdot ln(yi)=ln(β0)+β1⋅转为 y i ∗ = β 0 ∗ + β 1 ⋅ x i + u i y_{i}^{*}=\beta_0^*+\beta_1 \cdot x_{i}+u_i yi∗=β0∗+β1⋅xi+ui
△ Y Y = β 1 ⋅ △ x \frac{\vartriangle Y}{Y}=\beta_1 \cdot \vartriangle x Y△Y=β1⋅△x
既将Y的相对变化与x的绝对变化的关系,若将x转为△t则可视为增长模型
幂函数(全对数模型): y i = β 0 x i β 1 e u i y_i=\beta_0 x_i^{\beta_1}e^{u_i} yi=β0xiβ1eui转为 l n ( y i ) = l n ( β 0 ) + β 1 ⋅ l n ( x i ) + u i ln(y_i)=ln(\beta_0)+ \beta_1 \cdot ln(x_i)+u_i ln(yi)=ln(β0)+β1⋅ln(xi)+ui转为 y i ∗ = β 0 ∗ + β 1 ⋅ x i ∗ + u i y_{i}^{*}=\beta_0^*+\beta_1 \cdot x_{i}^*+u_i yi∗=β0∗+β1⋅xi∗+ui应用如生产函数
生长曲线logistics模型
k y = 1 + β i e − β 0 t + u t \frac{k}{y}=1+\beta_i e^{-\beta_0 t+u_t} yk=1+βie−β0t+ut转为 l n ( k y − 1 ) = l n ( β 1 ) − β 0 t + u t ln(\frac{k}{y}-1)=ln(\beta_1)-\beta_0 t+u_t ln(yk−1)=ln(β1)−β0t+ut转为 y i ∗ = β 0 ∗ − β 1 ⋅ x i + u i y_{i}^{*}=\beta_0^*-\beta_1 \cdot x_{i}+u_i yi∗=β0∗−β1⋅xi+ui
函数选择
1.边际函数、弹性函数
2.不能过分强调 R 2 R^2 R2这个指标
二、数据特征
1、处理异方差
2、自相关
3、多重共线性
4、虚拟变量的应用
5、F,LR,Wald,JB检验
三、面板数据类型
1、混合模型
2、固定效应模型
3、随机效应模型
四、其他
总结
提示:这里对文章进行总结:
例如:以上就是今天要讲的内容,本文仅仅简单介绍了pandas的使用,而pandas提供了大量能使我们快速便捷地处理数据的函数和方法。