计量经济学笔记1:简介
目录
什么是计量经济学?
计量经济学方法论
1. 理论或假说的陈述
2.消费的数学模型设定
3.消费的计量经济模型设定
变量间的函数关系
变量间的统计关系
4.获取数据
5.计量经济模型的参数估计
R软件一元线性回归分析简介
6.假设检验
7.预报或预测
8.利用模型进行控制或制定政策
什么是计量经济学?
从字面上解释,计量经济学(econometrics) 意谓“经济测量”。计量经济学可定义为这样的社会科学:它把经济理论、数学和统计推断作为工具,应用于经济现象的分析。
经济理论所作的陈述或假说大多数是定性的。例如,微观经济理论声称,在其他条件不变的情况下,一种商品的价格下降可望增加对该商品的需求量,即经济理论设想商品价格与其需求量之间存在一负向或逆向关系。但此理论并没有对两者的关系提供任何数值度量,也就是说,它没有说出随着商品价格的某一变化,需求量将会增加或者减少多少。计量经济的工作就是要提供这一数值估计。数理经济学的主要问题,是要用数学形式(方程式)来表述经济理论,而不管该理论是否可以量化或是否能够得到实证支持;而计量经济学对大多数的经济理论赋予经验内容,计量经济学的主要兴趣在于经济理论的经验论证。我们将看到,计量经济学常常使用数理经济学家所提供的数学方程式,但要把这些方程式改造成适合于经验检验的形式。这种从数学方程到计量经济方程的转换需要有许多的创造性和实际技巧。
经济统计学的问题主要是收集、加工并通过图表的形式来展现经济数据。经济统计学收集国内生产总值(GDP)、国民生产总值(GNP)、就业、失业、价格等数据,这些数据从此构成了计量经济工作的原始资料。但是经济统计的工作到此为止,不进一步考虑怎样利用所收集的数据去检验经济理论。
在计量经济学中,建模者通常面对的是观测(observational)数据而非实验(experimental)数据,即数据并非受控的实验结果(大多数经济数据的独特性)。这对计量经济学中的经验建模有两方面重要含义:首先,要求建模者掌握与分析实验数据极为不同的技巧;其次,数据搜集者与分析者的分离要求建模者十分熟悉所用数据的性质和结构。
计量经济学方法论
对于一个经济问题,计量经济学家是怎样进行分析的呢?他们的方法论是什么?尽管关于计量经济学的思想方法有了若干学派,但我们这里讲述的主要是至今仍在经济学及其他社会和行为科学领域的经验研究中占统治地位的传统(traditional) 或经典(classical) 方法论。
大致说来,传统的计量经济学方法论按如下路线进行:
- 理论或假说的陈述;
- 理论的数学模型设定;
- 统计或计量经济模型设定;
- 获取数据;
- 计量经济模型的参数估计;
- 假设检验;
- 预报或预测;
- 利用模型进行控制或制定政策。
为了说明以上步骤,让我们考虑如下著名的凯恩斯消费理论。
1. 理论或假说的陈述
凯恩斯说:基本的心理定律……是,通常或平均而言,人们倾向于随着他们收入的增加而增加其消费,但不如收入增加的那么多。
简言之,凯恩斯设想,边际消费倾向(marginal propensity to consume, MPC),即收入每变化一个单位的消费变化率,大于零而小于 ![]() .
.
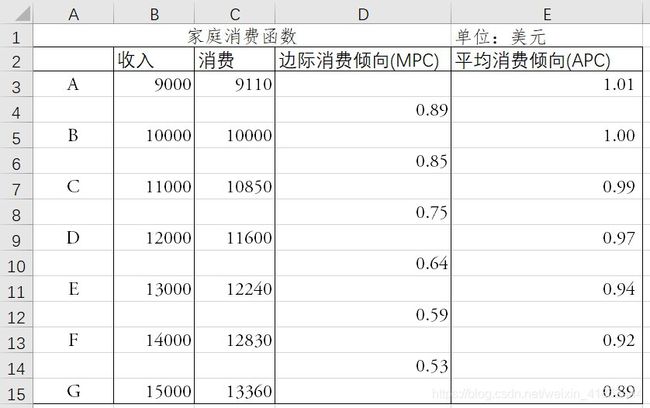
关于收入和消费的关系,凯恩斯认为,存在一条基本心理规律:随着收入的增加,消费也会增加,但是消费的增加不及收入的增加多,消费和收入的这种关系被称作消费函数或消费倾向,用公式表示是:![]() . 假定消费和收入之间有下表所示的关系:
. 假定消费和收入之间有下表所示的关系:
增加的消费与增加的收入之比率,也就是增加的一单位收入中用来消费的比率,被称为边际消费倾向(MPC). 边际消费倾向的公式为:![]()
> income<-c(9000,10000,11000,12000,13000,14000,15000)
> consumption<-c(9100,10000,10850,11600,12240,12830,13360)
> mpc<-numeric(length = length(consumption)-1)
>
> for (i in seq_along(mpc)) #函数seq_along(arg)有一个输入参数
+ #该函数根据参数变量的长度(length)创建相同长度的序列
+ {
+ mpc[i]<-(consumption[i+1]-consumption[i])/(income[i+1]-income[i])
+ }
> mpc
[1] 0.90 0.85 0.75 0.64 0.59 0.53
> install.packages("ggplot2")
> library(ggplot2)
> data=data.frame(income[-1],mpc)
> income=income[-1]
> consumption=consumption[-1]
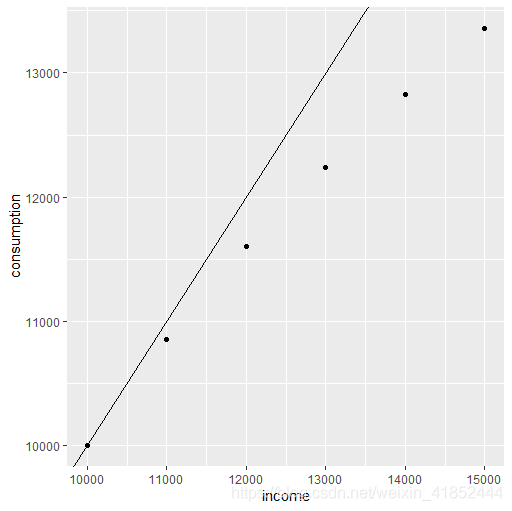
> ggplot(data,aes(income,consumption))+geom_point()+geom_abline(intercept=0,slope=1)
注意<是 R 的提示符,不是输入的命令的一部分,行号是微博编辑器加上的。R 代码生成的图像:
图中直线的斜率为1. 注意横纵坐标并非从 0 开始。
2.消费的数学模型设定
虽然凯恩斯假设消费与收入之间存在正向关系,但他没有明确指出二者之间准确的函数关系。为简单起见,数理经济学家也许建议采用如下形式的凯恩斯消费函数:
![]()
其中 ![]() 消费支出,
消费支出,![]() 收入,而被称为模型参数(parameter) 的
收入,而被称为模型参数(parameter) 的 ![]() 和
和 ![]() 分别代表截距(intercept) 和斜率(slope)系数。
分别代表截距(intercept) 和斜率(slope)系数。
斜率系数 ![]() 度量了边际消费倾向,为说明其几何意义,将(1)表示如图:
度量了边际消费倾向,为说明其几何意义,将(1)表示如图:
该方程表明消费与收入有线性关系。这种关系仅是消费与收入关系即经济学中所称的消费函数(consumption function)数学模型的一个例子。所谓数学模型就是一组数学方程,如果模型只有一个方程,像上例那样,就称之为单方程模型(single-equation model); 如果模型有不止一个方程,就称之为多方程模型(multiple-equation model)(后者将在以后讨论)。
出现在 ![]() 等号左边的变量称为因变量(dependent variable), 而出现在右边的变量(一个或多个)则称为自变量(independent variable)或解释变量(explanatory). 这样,在代表凯恩斯消费函数的方程(1)中,消费(支出)是因变量,而收入是解释变量。
等号左边的变量称为因变量(dependent variable), 而出现在右边的变量(一个或多个)则称为自变量(independent variable)或解释变量(explanatory). 这样,在代表凯恩斯消费函数的方程(1)中,消费(支出)是因变量,而收入是解释变量。
3.消费的计量经济模型设定
由方程(1)给出的消费函数纯数学模型,假定消费与收入之间有一个准确的或确定性的关系,因此它对计量经济学家的用处是有限的。一般地说,经济变量之间的关系是非准确的。例如,我们获得了(比如说)500个美国家庭消费支出和可支配收入的一个样本数据,并把这些数据画在以消费支出为纵坐标,以可支配收入为横坐标的图纸上,我们不能指望所有的观测值都恰好落在 Figure I.1 这条直线上,因为除了收入外,还有其他变量影响着消费支出。比方说,家庭规模、家庭成员的年龄、家庭的宗教信仰等,都对消费有一定的影响。
考虑到经济变量之间的非准确关系,计量经济学家会把确定性的消费函数(1)修改如下:
![]()
其中 ![]() 被称为干扰项(disturbance) 或误差项(error term), 是一个随机变量(random variable, stochastic variable), 它有良好定义的概率性质。干扰项
被称为干扰项(disturbance) 或误差项(error term), 是一个随机变量(random variable, stochastic variable), 它有良好定义的概率性质。干扰项 ![]() 可用来代表所有未经指明的对消费者有所影响的那些因素。
可用来代表所有未经指明的对消费者有所影响的那些因素。
变量间的函数关系
互有联系的经济现象及经济变量之间关系的紧密程度各不一样。一种极端的情况是一个变量的变化能完全决定另一个变量的变化。例如,一家保险公司承保汽车5万辆,每辆保费收入为1000元,则该保险公司汽车承保总收入为5000万元。如果把承保总收入记为 ![]() , 承保汽车辆数记为
, 承保汽车辆数记为 ![]() , 则
, 则 ![]() .
. ![]() 与
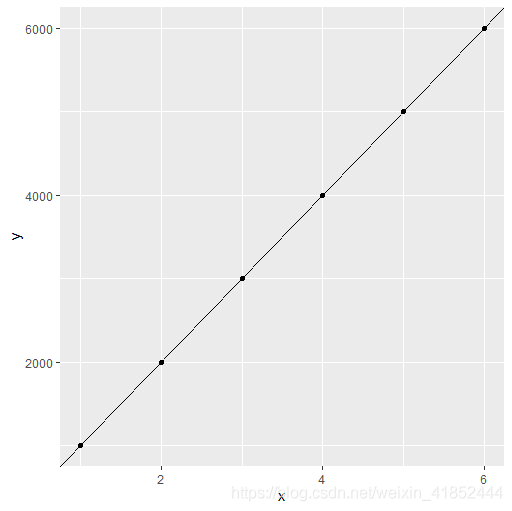
与 ![]() 两个变量间完全表现为一种确定性关系,即函数关系,如下图所示:
两个变量间完全表现为一种确定性关系,即函数关系,如下图所示:
生成图像的 R 代码
> x<-1:6
> y<-1000*x
> library(ggplot2)
> data=data.frame(x,y)
> ggplot(data,aes(x,y))+geom_point()+geom_abline(intercept=0,slope=1000)又如,银行的一年期存款利率为 2.55%, 存入的本金用 ![]() 表示,到期的本息用
表示,到期的本息用 ![]() 表示,则
表示,则 ![]() . 这里
. 这里 ![]() 与
与 ![]() 仍表现为一种线性函数关系。对于任意两个变量间的函数关系,可以表述为下面的数学形式
仍表现为一种线性函数关系。对于任意两个变量间的函数关系,可以表述为下面的数学形式
![]()
我们可以将变量 ![]() 与
与 ![]() 个变量
个变量 ![]() 之间存在的某种函数关系用下面的形式表示
之间存在的某种函数关系用下面的形式表示
![]()
物理学中的自由落体距离公式、初等数学中的许多计算公式等表示的都是变量间的函数关系。
变量间的统计关系
然而,现实世界中还有不少情况是两事物之间有着密切的联系,但它们密切的程度没有到由一个可以完全确定另一个。下面举几个例子:
- 我们都知道某种高档消费品的销售量与城镇居民的收入密切相关,居民收入高,这种消费品的销售量就大。但是居民收入
 并不能完全确定某种高档消费品的销售量
并不能完全确定某种高档消费品的销售量  , 因为这种高档消费品的销售量还受人们的消费习惯、心理因素、其他消费品的吸引程度及价格的高低等诸多因素的影响。这样变量
, 因为这种高档消费品的销售量还受人们的消费习惯、心理因素、其他消费品的吸引程度及价格的高低等诸多因素的影响。这样变量  与变量
与变量  就是一种非确定的关系。
就是一种非确定的关系。 - 粮食产量
 与施肥量
与施肥量  之间有密切的关系,在一定的范围内,施肥量越多,粮食产量就越高。但是,施肥量并不能完全确定粮食产量,因为粮食产量还与其他因素有关,如降雨量、田间管理水平等。因此粮食产量
之间有密切的关系,在一定的范围内,施肥量越多,粮食产量就越高。但是,施肥量并不能完全确定粮食产量,因为粮食产量还与其他因素有关,如降雨量、田间管理水平等。因此粮食产量  与施肥量
与施肥量  之间不存在确定的函数关系。
之间不存在确定的函数关系。 - 储蓄额与居民的收入密切相关,但是由居民收入并不能完全确定储蓄额。因为影响储蓄额的因素很多,如通货膨胀、股票价格指数、利率、消费观念、投资意识等。因此尽管储蓄额与居民收入有密切的关系,但它们之间并不存在一种确定性关系。
再如广告费支出与商品销售额、工业产值与用电量等。这方面的例子不胜枚举。以上三个例子中变量间关系的一个共同特征是尽管密切,但却是一种非确定性关系。由于经济问题的复杂性,有许多因素因为我们的认知以及其他客观因素的局限,并没有被考虑在内,或者由于试验误差、测量误差以及其他种种偶然因素的影响,使得当一个或者一些变量取定值后,另外一个或一些变量的取值带有一定的随机性。在推断统计中,我们把上述变量间具有密切关联而又不能由一个或某一些变量唯一确定另外一个变量的关系称为变量间的统计关系或相关关系。这种统计关系的规律性是统计学中研究的主要对象,现代统计学中关于统计关系的研究已形成两个重要的分支,它们叫回归分析和相关分析。
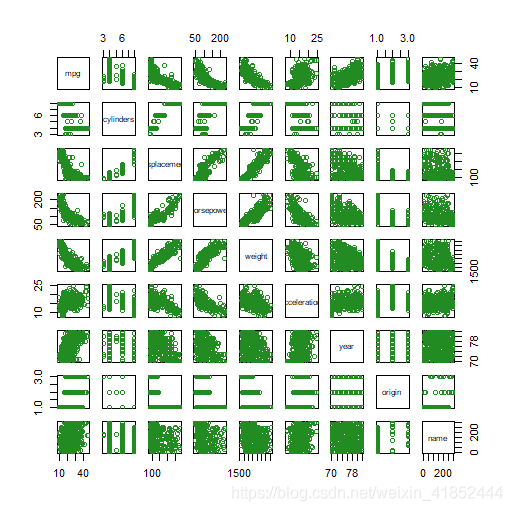
先简要讨论一个数据来自真实世界的、变量之间为统计关系的例子 Auto. Auto 数据的数据格式为数据框(data frame). 当数据被载入后,用 fix() 函数可以开启一个电子表格窗口来浏览数据。
> install.packages("ISLR")
> library(ISLR)
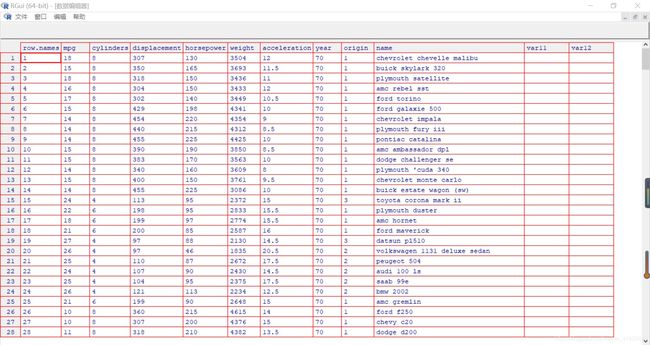
> fix(Auto)
将 fix() 函数弹出的窗口最大化,
然而,在有新的 R 命令被应用之前这个窗口需要被关闭。在某个数据集被正确加载后,因为 R 假定变量名称也是数据的一部分,所以会在数据的第一行列出这些变量名。na.omit()用来剔除有缺失数据的行
> library(ISLR)
> dim(Auto)
[1] 392 9
> Auto[1:6,]
mpg cylinders displacement horsepower weight acceleration year origin name
1 18 8 307 130 3504 12.0 70 1 chevrolet chevelle malibu
2 15 8 350 165 3693 11.5 70 1 buick skylark 320
3 18 8 318 150 3436 11.0 70 1 plymouth satellite
4 16 8 304 150 3433 12.0 70 1 amc rebel sst
5 17 8 302 140 3449 10.5 70 1 ford torino
6 15 8 429 198 4341 10.0 70 1 ford galaxie 500
> Auto=na.omit(Auto)
> dim(Auto)
[1] 392 9
> names(Auto)
[1] "mpg" "cylinders" "displacement" "horsepower" "weight" "acceleration"
[7] "year" "origin" "name"
用 pairs() 函数可建立一个对任何指定数据集中每一对变量的散点图矩阵。
> pairs(Auto,col="forestgreen")回到
![]()
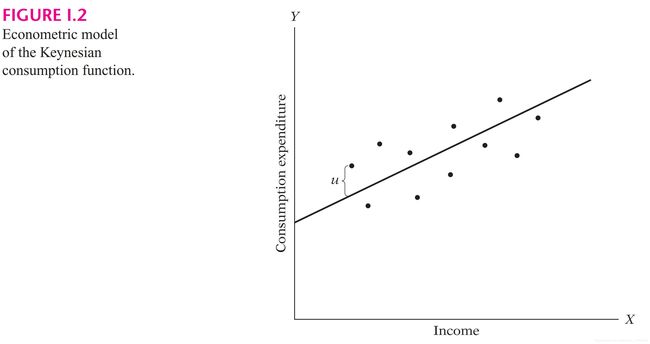
方程(2) 是计量经济模型(econometric model) 之一例。更技术地讲,它是本书主要论述的线性回归模型(linear regression model) 之一例。该计量经济消费函数假设了因变量 ![]() (消费)与解释变量
(消费)与解释变量 ![]() (收入)之间存在线性关系。然而两者的关系不是准确的,它随着家庭的变化而有所变化。
(收入)之间存在线性关系。然而两者的关系不是准确的,它随着家庭的变化而有所变化。
可把消费函数的计量经济模型描绘成图 I.2 这样
4.获取数据
为了估计
![]()
给出的计量经济模型,也就是为了得到 ![]() 和
和 ![]() 的数值,需要有数据。虽然我们之后要更详细地讨论数据对经济分析的根本重要性,但现在不妨先看一下美国经济在 1960-2005 年间的数据,如表 I-1 所示:
的数值,需要有数据。虽然我们之后要更详细地讨论数据对经济分析的根本重要性,但现在不妨先看一下美国经济在 1960-2005 年间的数据,如表 I-1 所示:
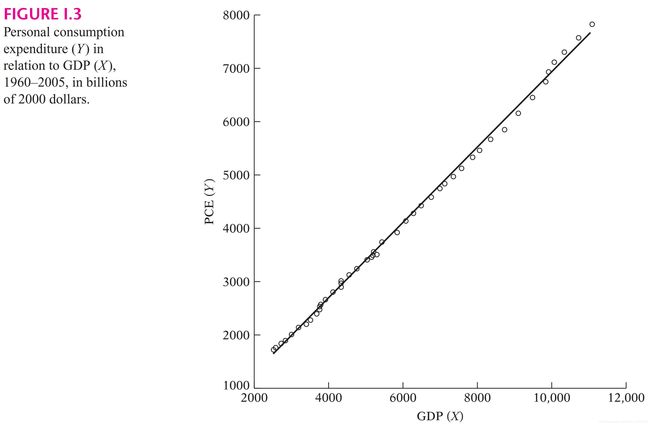
该表中的 ![]() 变量是(整个国家)个人消费支出(PCE, personal consumption expenditure) 的加总,而
变量是(整个国家)个人消费支出(PCE, personal consumption expenditure) 的加总,而 ![]()
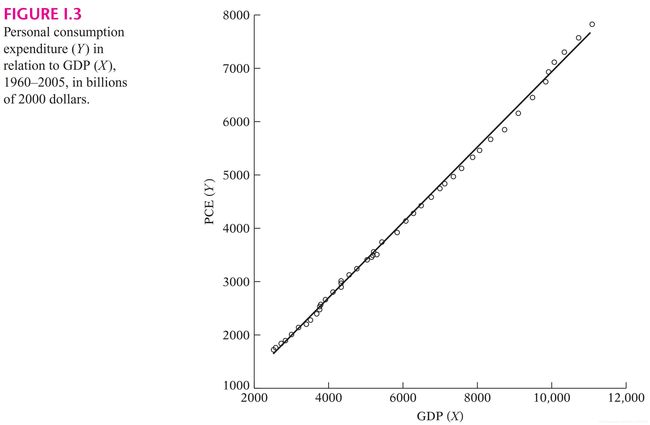
![]() 变量是国内生产总值(GDP), 度量了美国的总收入,均以 2000 年不变美元价格计算,单位是十亿美元。因此,所列数据代表以 2000 年不变价格计算的“真实”消费和“真实”收入。现将这些数据描绘在图 I.3 上,暂不考虑图中所画的直线。
变量是国内生产总值(GDP), 度量了美国的总收入,均以 2000 年不变美元价格计算,单位是十亿美元。因此,所列数据代表以 2000 年不变价格计算的“真实”消费和“真实”收入。现将这些数据描绘在图 I.3 上,暂不考虑图中所画的直线。
5.计量经济模型的参数估计
有了数据之后,下一步的任务就是估计消费函数中的参数。参数的数值估计将对消费函数赋予经验内容。估计参数的具体步骤将在之后的博文中说明。这里仅指出,回归分析(regression analysis) 的统计学方法是获得估计值的主要手段。利用这种方法以及表 I.1 所给的数据,我们便得到 ![]() 和
和 ![]() 的估计值为
的估计值为 ![]() 和
和 ![]() . 于是所估计的消费函数是
. 于是所估计的消费函数是
![]()
![]() 顶上的帽符表示它是估计值。图 I.3 给出了估计的消费函数(即回归线)。之后的博文中将介绍给出这些估计值最小二乘统计方法(least squares),这里暂且不去管它们是怎样得来的、为什么截距是负值。
顶上的帽符表示它是估计值。图 I.3 给出了估计的消费函数(即回归线)。之后的博文中将介绍给出这些估计值最小二乘统计方法(least squares),这里暂且不去管它们是怎样得来的、为什么截距是负值。
R软件一元线性回归分析简介
这里所用到的数据变量之间为统计关系而非确定的函数关系。在回归分析中,把变量分成两类。一是因变量,它们通常是实际问题中所关心的一些指标,通常用 ![]() 表示,而影响因变量取值的另一些变量称为自变量,它们用
表示,而影响因变量取值的另一些变量称为自变量,它们用 ![]() 来表示。
来表示。
在回归分析中研究的主要问题是:
- 确定
 与
与 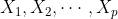 间的定量关系表达式,这种表达式称为回归方程;
间的定量关系表达式,这种表达式称为回归方程; - 对求得的回归方程的可信度进行检验;
- 判断自变量
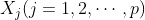 对
对  有无影响;
有无影响; - 利用所求得的回归方程进行预测和控制。
先从最简单的情况开始讨论,只考虑一个因变量 ![]() 与一个自变量
与一个自变量 ![]() 之间的关系。下面我们通过一个例子来说明如何寻找
之间的关系。下面我们通过一个例子来说明如何寻找 ![]() 与
与 ![]() 之间的定量关系表达式。
之间的定量关系表达式。
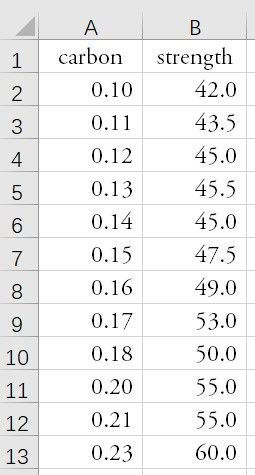
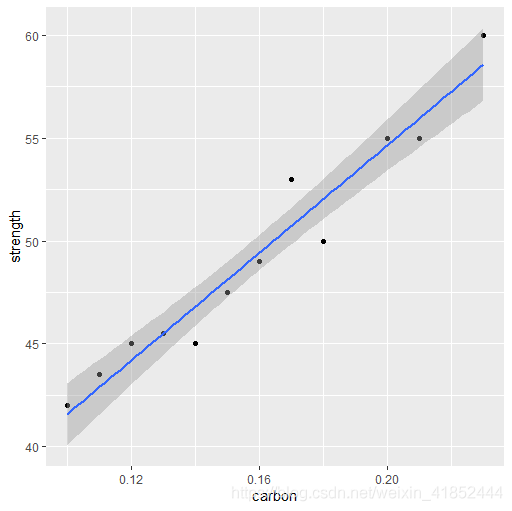
由专业知识知道,合金的强度 ![]() 与合金中碳含量
与合金中碳含量 ![]() 有关。为了了解它们间的关系,从生产中收集了一批数据
有关。为了了解它们间的关系,从生产中收集了一批数据 ![]() , 具体数据见下表:
, 具体数据见下表:
为了直观起见,可画一张“散点图”,以 ![]() 为横坐标,
为横坐标,![]() 为纵坐标,每一数据对
为纵坐标,每一数据对 ![]() 为
为 ![]() 坐标中的一个点,
坐标中的一个点,![]() ,如下图所示:
,如下图所示:
library(ggplot2)
ggplot(data, aes(carbon,strength)) + geom_point() + geom_smooth(method="lm")在本例中,从散点图上发现,上面例子的样本数据点 ![]() 大致分别落在一条直线附近。这说明变量
大致分别落在一条直线附近。这说明变量 ![]() 与 变量
与 变量 ![]() 之间具有很明显的线性关系。从图上还可以看到,这些样本点又不在一条直线上,这表明
之间具有很明显的线性关系。从图上还可以看到,这些样本点又不在一条直线上,这表明 ![]() 和
和 ![]() 的关系并没有确切到给定
的关系并没有确切到给定 ![]() 就可以唯一确定
就可以唯一确定 ![]() 的程度。每个样本点与直线的偏差就可以看作其他随机因素的影响。
的程度。每个样本点与直线的偏差就可以看作其他随机因素的影响。
> attach(data)
The following objects are masked from data (pos = 3):
carbon, strength
> lm.carb<-lm(strength~carbon)
> summary(lm.carb)
Call:
lm(formula = strength ~ carbon)
Residuals:
Min 1Q Median 3Q Max
-2.0431 -0.7056 0.1694 0.6633 2.2653
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 28.493 1.580 18.04 5.88e-09 ***
carbon 130.835 9.683 13.51 9.50e-08 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.319 on 10 degrees of freedom
Multiple R-squared: 0.9481, Adjusted R-squared: 0.9429
F-statistic: 182.6 on 1 and 10 DF, p-value: 9.505e-08
计算结果的第一部分(Call:) 列出了相应的回归模型的公式。第二部分(Residuals:) 列出的是残差的最小值点、![]() 分位点,中位数点,
分位点,中位数点,![]() 分位点和最大值点。在计算结果的第三部分中, Estimate 表示回归方程参数的估计,即和
分位点和最大值点。在计算结果的第三部分中, Estimate 表示回归方程参数的估计,即和
![]()
对应的 ![]() . 更详细的内容将在今后的博文中进一步解释。
. 更详细的内容将在今后的博文中进一步解释。
回到图I.3
如图 I.3 所示,因为数据点很靠近回归线,所以回归线对数据拟合的相当好。从图 I.3 我们发现,在 1960-2005 年间,斜率系数(即 MPC)约为 0.72, 表明在此样本期间,真实收入每增加 1 美元,平均而言,真实消费支出将增加约 72 美分。我们说平均而言,是因为消费和收入之间没有准确的关系。这一点可以从图 I.3 中看出:并非所有的数据点都恰好位于回归线上。我们可以简单地说,根据我们的数据,真实收入每增加 1 美元,平均消费支出或消费支出均值会增加约72美分。
6.假设检验
假定所拟合的模型是现实的一个较好的近似,还必须制定适当的准则,借以判断如方程
![]()
中的估计值是否与待检验的理论预期相一致。根据米尔顿 • 弗里曼(Milton Friedman) 这样的 “实证” 经济学家的意见,凡是不能通过经验证据来证实的理论或假设,都不可作为科学探索的一个部分。
如前所述,凯恩斯曾预期 MPC 是正的,但小于 1. 在我们的例子中,我们求得 MPC 约为 0.72. 但在把这一发现看做是对凯恩斯消费理论的认可之前,还要追问这一估计值是否充分地低于 1,以使我们不再怀疑这个估计值仅是一次偶然的机会得来,或者怀疑我们用的数据太特殊了。换言之, 0.72 是不是在统计意义上小于 1? 如果是,就可用来支持凯恩斯理论。
以样本证据为依据去肯定或否定经济理论,是以所谓统计推断(statistical inference, 即假设检验 hypothesis testing) 这个统计理论分支为基础的。
7.预报或预测
如果所选的模型肯定了我们所考虑的假说或理论,就可以根据解释变量或预测变量(predictor variable) ![]() 的已知或预期未来值,来预测因变量或预报变量(forecast variable)
的已知或预期未来值,来预测因变量或预报变量(forecast variable) ![]() 的未来值。
的未来值。
为了便于说明,假设我们想预测 2006 年的平均消费支出。 2006 年 GDP 的值为 113194 亿美元(有 2006 年 PCE 和 GDP 的数据可用, 但我们在说明本节所讨论的专题时故意不用。如同我们在以后章节中所讨论的那样,留下一部分数据用来检查拟合模型对样本外观测的预测力如何,是一个很好的主意,这里公式中的单位均为十亿美元)。将 GDP 的这个数字代入
![]()
的右边,我们得到:
![]()
即约 78700 亿美元。 因此,给定 GDP 的值,预测的平均消费支出或消费支出的均值约为 78700 亿美元。2006 年报告的实际消费支出值为 80440 亿美元。于是估计模型 (3) 约低估(underpredicted) 了实际消费支出 1740 亿美元。我们可以说预测误差(forecast error) 约为 1740 亿美元, 占 2006 年实际 GDP 值的 1.5%. 当我们在之后的博文中详尽讨论了线性回归模型后,我们会发现这样的误差是“小”还是“大”。但目前重要的是注意到,给定这种分析的统计性质,这种预测误差无法避免。
模型 (3) 还有另外一个用处。假设总统决定减少所得税。这种政策对收入及消费支出和最终就业有什么影响呢?
假设政策改变的结果是投资有所下降,其对经济的影响将如何?宏观经济理论告诉我们,投资支出每改变 1 元, 收入的改变由收入乘数(income multiplier, M):
给出。如利用由方程 (3) 得到的 MPC=0.72, 此乘数就变成 M=3.57. 也就是说,投资减少(增加)1 美元,将最终导致收入减少(增加)4倍之多;注意,乘数的实现需要时间。
这一计算中 MPC 是个关键值,因为乘数的大小取决于它。但 MPC 的估计来自诸如(3) 的回归模型。所以, MPC 的数量估计为政策的制定提供了有价值的信息。一旦获知 MPC, 即可跟踪政府财政政策的改变,预测收入和消费支出的未来变化过程。
8.利用模型进行控制或制定政策
若我们已估计出由方程(3) 给出的凯恩斯消费函数,而且政府认为 87500 亿美元(以 2000 年美元计)的(消费)支出水平即可维持当前约 4.2% 的失业率(2006年初),那么,什么样的收入水平即可维持当前约 4.2% 的失业率(2006年初),那么,什么样的收入水平将保证消费支出达到这个目标水平呢?
如果消费函数 (3) 是合理的,简单的数学运算就得到:
![]()
解得 ![]() . 也就是说,给定 MPC 约为 0.72, 125370 亿美元的收入水平将导致约 87500 亿美元的消费支出。
. 也就是说,给定 MPC 约为 0.72, 125370 亿美元的收入水平将导致约 87500 亿美元的消费支出。
上述计算提示我们,一个已估计出来的模型可服务于控制或政策的目的。通过适当的财政与货币政策的配合,政府可操纵控制变量(control variable) ![]() 以实现目标变量(target variable)
以实现目标变量(target variable) ![]() 的某个理想水平。
的某个理想水平。