【异常检测】LSTM用于异常检测:DeepLog与Machine Unlearning
动态异常检测
分析系统运行日志可以检测出系统异常,Min Du ICDM’16的文章SPELL提出一个日志解析工具;基于这个工作,她在CSS’17提出了DeepLog,也是现在非常经典的baseline,无监督的检测系统运行日志;她在CCS’19的工作在DeepLog的基础上引入了恶意样本的信息,改进准确率和误报率,并且将模型适用场景泛化到了信用卡交易记录等。
一、DeepLog
《DeepLog: Anomaly Detection and Diagnosis from System Logs through Deep Learning》 (CCS’17)
1、Abstract
Log记录系统的状态和重要事件,这篇文章将Log当作自然语言序列来处理(实际上其实是更“干净”语言序列,因为相比语言log遵循严格的逻辑和控制流)。DeepLog本质是个深度学习模型,提取正常运行的log的模式特征,当log信息偏离训练的模型时检测出异常。这篇文章还提出如何在线更新迭代DeepLog模型。
2、Introduction
2.1、 Existing Work
总的来说还是基于传统统计方法(2017年之前)
- 基于log消息计数的PCA聚类
- invariant mining based methods to capture co-occurrence partterns between different log
keys - workflow-based方法识别程序逻辑流的执行异常
上述方法只在限定场景有效,不能防御线上场景中的各种攻击
2.2 Challenges
现有的一些方法使用rule-based方法,需要很强的领域知识。异常检测只有及时才有用,分类决策需要随着工作流产生。日志消息是并发的。
贡献
通过观察,系统日志中的条目是由执行结构化源代码产生的一系列事件(因此可以视为结构化语言)。模型先在一个小的、正常的log数据集上训练,然后在工作流中可以识别正常log,检测出异常情况。
在HDFS log、OpenStack log数据集上,DeepLog可以在1%的数据上训练,然后几乎100%预测剩下的99%的log。
DeepLog可以动态学习(online learning)。
3、Approach
3.1 日志解析
首先要把非结构化数据log解析成结构化数据,即从log entry中解析出“log key”。对于一个log entry的log key e e e 指源代码中打印语句中的字符串常数k,该字符串常数在执行该代码时打印出e。例如:
解析出来的数据格式如下:
key + [前一个log的时间差,parameter values] 模型就用这三种信息
3.2 Deeplog架构概览
( k + 1 ) (k+1) (k+1)个模型
三部分组成:
- log key异常检测模型(1个)
- parameter value异常检测模型(k个)
- workflow模型诊断异常
值得注意的是对于每个log key k k k,DeepLog各自训练一个模型( k k k个模型),用 k k k的参数向量序列来训练。
识别阶段,一个新来的log先被解析成log key + 参数向量序列。log key模型先检查来的log key是否异常,如果正常,再用log key对应的参数检查模型去检查参数向量序列是否异常。如果异常,送给用户诊断。
如果把白样本误报成了黑样本,模型可以迭代更新训练。
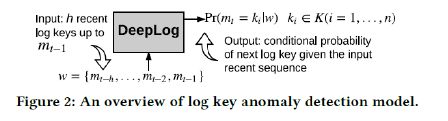
4、 异常检测
运行日志log key的词典大小 K = { k 1 , k 2 , … , k n } K=\left\{k_{1}, k_{2}, \ldots, k_{n}\right\} K={k1,k2,…,kn},模型是一个多类分类器,每次输入一个窗口长度的log key序列 w = { m t − h , … , m t − 2 , m t − 1 } w=\left\{m_{t-h}, \ldots, m_{t-2}, m_{t-1}\right\} w={mt−h,…,mt−2,mt−1} ,异常触发的条件是预测错(不在top g个预测中)。
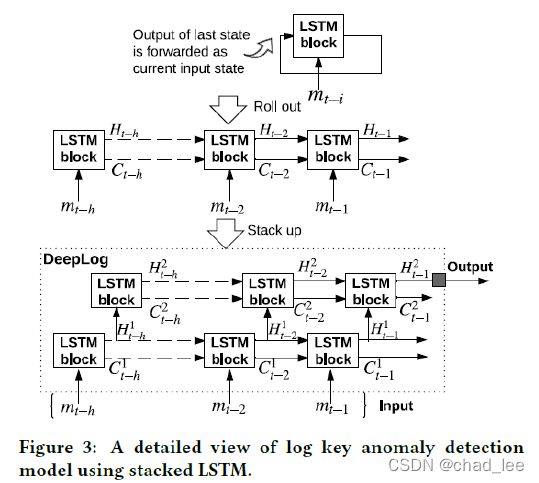
模型用的是多层LSTM,但是其实数据集和代码都比较简单,log key序列的词典大小只有28,并且观察数据集也比较有规律,有比较明显的区分(这也归功于作者自己ICDM16的工作)。
DeepLog剩下的k个LSTM模型是分析这个log key对应的log中的参数,以及log间隔时间。这部分序列主要可以识别出DoS攻击(间隔时间长)等。这个部分模型的作用感觉很弱,作者在报告时也没有很强调这部分,Github上开源的代码索性没实现这部分。
其他内容
文章还有很多内容是提出在线异常检测的工作流、online learning等等和我们现在的工作关系不大。
效果
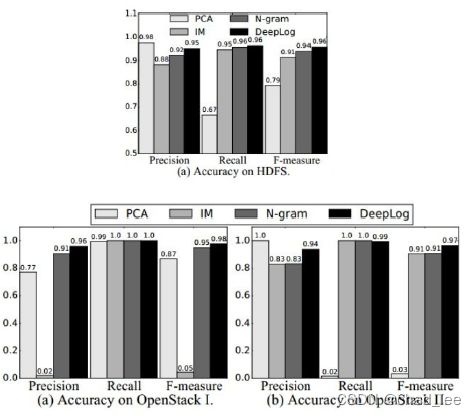
log key效果
作者在1%的数据集上训练,几乎可以预测出剩下99%的数据。
二、Lifelong Anomaly Detection Through Unlearning(CCS’19)
上文在DeepLog中,模型上线后的在线更新是:将误报的白样本(FN)提供给模型进行学习训练,那么问题来了:黑样本的信息从来没有被引入过,尽管存在可用的黑样本。所以本文增加了利用FP来更新模型。
但是Unlearning会带来梯度爆炸和catastrophic forgetting,文章也提出了解决办法。
LSTM异常检测
Unlearning 更新模型
对于一个黑样本,被误报成正常样本,即概率值超过了阈值:
Pr ( x t ) > τ (1) \operatorname{Pr}\left(x_{t}\right)>\tau \tag {1} Pr(xt)>τ(1)
其中 τ \tau τ是阈值,等价于损失函数低于了某个阈值:
L ( x t ) < τ ′ (2) \mathcal{L}\left(x_{t}\right)<\tau^{\prime}\tag {2} L(xt)<τ′(2)
我们为了减小 Pr ( x t ) \operatorname{Pr}\left(x_{t}\right) Pr(xt)的可能性,等价于增大损失函数 L ( x t ) \mathcal{L}\left(x_{t}\right) L(xt)的值,因此:
L unlearn ( x t ) = − L ( x t ) (3) \mathcal{L}_{\text {unlearn}}\left(x_{t}\right)=-\mathcal{L}\left(x_{t}\right)\tag {3} Lunlearn(xt)=−L(xt)(3)
同样的可以应用优化算法最小化 L unlearn ( x t ) \mathcal{L}_{\text {unlearn}}\left(x_{t}\right) Lunlearn(xt),得到梯度:
∇ θ L unlearn ( x t ) = ∇ θ ( − L ( x t ) ) = − ∇ θ L ( x t ) (4) \nabla_{\theta} \mathcal{L}_{\text {unlearn }}\left(x_{t}\right)=\nabla_{\theta}\left(-\mathcal{L}\left(x_{t}\right)\right)=-\nabla_{\theta} \mathcal{L}\left(x_{t}\right)\tag {4} ∇θLunlearn (xt)=∇θ(−L(xt))=−∇θL(xt)(4)
θ new ← θ old − η ⋅ ∇ θ L umlearn ( x t ) = θ old + η ⋅ ∇ θ L ( x t ) (5) \theta_{\text {new }} \leftarrow \theta_{\text {old }}-\eta \cdot \nabla_{\theta} \mathcal{L}_{\text {umlearn }}\left(x_{t}\right)=\theta_{\text {old }}+\eta \cdot \nabla_{\theta} \mathcal{L}\left(x_{t}\right)\tag {5} θnew ←θold −η⋅∇θLumlearn (xt)=θold +η⋅∇θL(xt)(5)
对于有标签的集合 S = { x t , l t } S = \{ x_t, l_t \} S={xt,lt}, L unlearn ( S ) \mathcal{L}_{\text {unlearn }}(S) Lunlearn (S):
L unlearn ( S ) = − ∑ t l t L ( x t ) (6) \mathcal{L}_{\text {unlearn }}(S)=-\sum_{t} l_{t} \mathcal{L}\left(x_{t}\right)\tag {6} Lunlearn (S)=−t∑ltL(xt)(6)
用SGD更新时:
θ n e w ← θ o l d + η ∑ t l t ⋅ ∇ θ L ( x t ) (7) \theta_{\mathrm{new}} \leftarrow \theta_{\mathrm{old}}+\eta \sum_{t} l_{t} \cdot \nabla_{\theta} \mathcal{L}\left(x_{t}\right)\tag {7} θnew←θold+ηt∑lt⋅∇θL(xt)(7)
梯度爆炸
最大化FN(黑样本误报白样本)的loss L ( x t ) \mathcal{L}\left(x_{t}\right) L(xt)可能会导致 L ( x t ) \mathcal{L}\left(x_{t}\right) L(xt)相当的大,这也会导致正常白样本的 L ( x i ) \mathcal{L}\left(x_{i}\right) L(xi)增大,从而导致模型完全失效了。
因此重新设计了loss function。对于一系列正常样本 x 1 , … , x t − 1 x_{1}, \ldots, x_{t-1} x1,…,xt−1, x t x_t xt是恶意样本:
∑ i = 1 t − 1 L ( x i ) − L ( x t ) (8) \sum_{i=1}^{t-1} \mathcal{L}\left(x_{i}\right)-\mathcal{L}\left(x_{t}\right)\tag {8} i=1∑t−1L(xi)−L(xt)(8)
如果不考虑最后一个负项,最小化目标就是减小每个独立 L ( x t ) \mathcal{L}\left(x_{t}\right) L(xt)的值(每项下界是0),假设最小化的值加起来是 τ \tau τ,那么对于每个 L ( x i ) \mathcal{L}\left(x_{i}\right) L(xi)的上界就是 τ \tau τ。那么 Pr ( x t ) \operatorname{Pr}\left(x_{t}\right) Pr(xt)就有一个下界(例如 e x p ( − τ ) exp(-\tau) exp(−τ)),因此我们可以根据这个下界来构建一个检测模型。
当考虑最后一个负项时,最小化目标可能导致只增大 L ( x t ) \mathcal{L}\left(x_{t}\right) L(xt),使得 L ( x i ) \mathcal{L}\left(x_{i}\right) L(xi)相当大,从而 P r ( x i ) Pr(x_i) Pr(xi)接近 0 % 0\% 0%。这会导致模型预测任何项都是恶意的。
为了应对这种情况,提出了两种方法:bounding loss和learning rate shrinking。
Bounding loss
ReLU ( B N D − l t L ( x t ) ) (9) \operatorname{ReLU}\left(B N D-l_{t} \mathcal{L}\left(x_{t}\right)\right)\tag{9} ReLU(BND−ltL(xt))(9)
L unlearn ( S ) = ∑ t ReLU ( B N D − l t L ( x t ) ) (10) \mathcal{L}_{\text {unlearn }}(S)=\sum_{t} \operatorname{ReLU}\left(B N D-l_{t} \mathcal{L}\left(x_{t}\right)\right)\tag {10} Lunlearn (S)=t∑ReLU(BND−ltL(xt))(10)
那么问题来了,边界BND怎么选,一个简单的想法是让 B N D = τ ′ BND = {\tau}^{\prime} BND=τ′, τ ′ \tau^{\prime} τ′是公式 ( 2 ) (2) (2)中的阈值。这样做的话一旦 L ( x t ) > τ \mathcal{L}\left(x_{t}\right)>\tau L(xt)>τ,unlearning algorithm就知道该停止了。但是这样做的话有个问题就是优化算法最小化公式 ( 10 ) (10) (10)时,可能会陷入公式(9)的局部最优,然而(9)依然还是一个而已样本。这样的话模型会将所有的FN预测为N(恶意->正常)。
一个实用的方法是让 B N D BND BND比 τ ′ \tau^{\prime} τ′稍微高一点,实验试出来是 B N D = 2 τ ′ B N D=2 \tau^{\prime} BND=2τ′最好。
learning rate shrinking
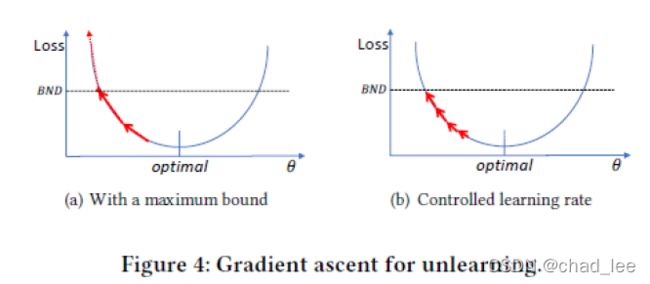
最大化 L ( x t ) \mathcal{L}\left(x_{t}\right) L(xt)时梯度的量级增大的很快,这个时候学习率不对应变化量级的话,模型性能下降的很快,尽管设置了 B N D BND BND,如图4(a)。RMSProp和Adam都不能解决这个问题。
所以这里设置学习率缩小为1%,可以unlearning的同时不伤害正常样本。另外,使学习过程更有效,可以在每次梯度更新后评估 L ( x t ) \mathcal{L}\left(x_{t}\right) L(xt),一旦其超过了边界 B N D BND BND,就停止。如图4(b).
阻止灾难性遗忘(catastrophic forgetting)
The basic idea is to keep the updated model “close" to the original model so that their performances on previously trained data are close as well.
实现:加正则化项:
L ( x t ) = ReLU ( B N D − l t L ( x t ) ) + λ 2 ⋅ ∥ θ − θ ⋆ ∥ 2 (11) \mathcal{L}\left(x_{t}\right)=\operatorname{ReLU}\left(B N D-l_{t} \mathcal{L}\left(x_{t}\right)\right)+\frac{\lambda}{2} \cdot\left\|\theta-\theta^{\star}\right\|^{2}\tag {11} L(xt)=ReLU(BND−ltL(xt))+2λ⋅∥θ−θ⋆∥2(11)
其中 θ ⋆ \theta^{\star} θ⋆是旧参数值。作者实验发现无论 λ \lambda λ设置多少,都会限制unlearning效果,因此修改为:
L ( x t ) = ReLU ( B N D − l t L ( x t ) ) + λ 2 ∑ i w i ( θ i − θ i ⋆ ) 2 (12) \mathcal{L}\left(x_{t}\right)=\operatorname{ReLU}\left(B N D-l_{t} \mathcal{L}\left(x_{t}\right)\right)+\frac{\lambda}{2} \sum_{i} w_{i}\left(\theta_{i}-\theta_{i}^{\star}\right)^{2}\tag {12} L(xt)=ReLU(BND−ltL(xt))+2λi∑wi(θi−θi⋆)2(12)
w i w_i wi计算方法:
w i = 1 ∣ M t ∣ ∑ x ∈ M t ( ∂ L ( x ) ∂ θ i ) 2 (13) w_{i}=\frac{1}{\left|M_{t}\right|} \sum_{x \in M_{t}}\left(\frac{\partial \mathcal{L}(x)}{\partial \theta_{i}}\right)^{2}\tag {13} wi=∣Mt∣1x∈Mt∑(∂θi∂L(x))2(13)
这个时候作者又维护了一个 M t M_t Mt:我们想让模型在时刻 t t t 时记住的一个有标签的小数据集。
感觉这个解决方案一点都不优雅,绕来绕去复杂又不直接。
和DeepLog效果对比
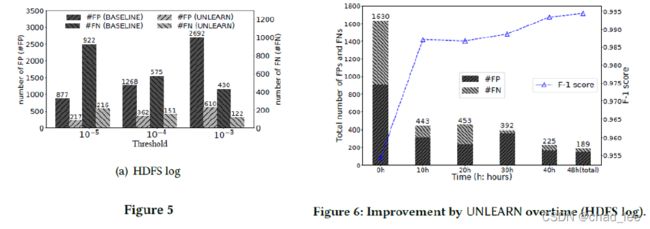
BASELINE是DeepLog,误报率低了很多,Fig 5。
并且随着时间推移可以提高准确率、减少误报,Fig 6。
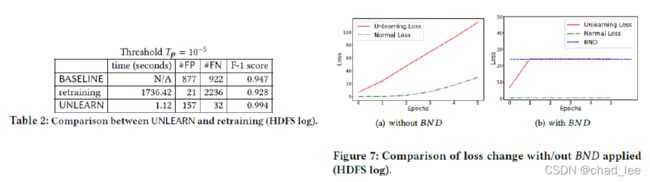
而且相较于重新训练,UNLEAN效果最好(主要是可以引入黑样本),Table 2。
为Unlearning loss加了上界,不会伤害正常的loss,Fig 7。