【推荐系统中的Hash 3】Deep Hash：Learning to Embed Categorical Features without Embedding Tables KDD‘21

三、深度哈希（id——embedding）

《Learning to Embed Categorical Features without Embedding Tables for Recommendation》Google KDD 2021 Research Track

文章以 NLP的视角切入推荐系统中embedding的问题：

• NLP中存在分词的机制，所以词表大小远远小于推荐中纯ID类的词表；
• NLP中的词表是静态的（因为词语是固定的），而推荐中词表需要经常更新（因为有新用户等进入）；
• 推荐中的高度偏移的数据分布，也就是如何处理长尾数据的embedding

文章提出Deep Hash Embeddings (DHE) 的方式来缓解以上问题，AUC相等的情况下模型参数量更少。

现有方法

One-hot full embedding

这种方式就是最常见的方法，即把所有类别特征进行编号，假设共 n 个特征。特征s 首先通过one-hot进行编码 $E(s)=b=\{0,1{\}}^n$ , 其中只有第 $b_s$ 项为1，其他都为0。接着通过一个可学习的线性变换矩阵（说白了就是embedding table，可以看作一层神经网络，但没有bias项）得到对应的embedding表示：$e=W^{T}b$ 。

这种方法的缺点：1、embedding table随特征数量线性增长（即内存问题）；2、无法处理新出现的特征（OOV）。

One-hot Hash Embedding

为了解决One-hot Full Embedding中的内存消耗巨大的问题，可以使用**「哈希函数」对类别特征进行「映射分桶」**，将原始的 n 维的 one-hot 特征编码映射为 m 维的 one-hot 特征编码（即m个桶，$m<<n$ ）。这样，embedding table只用存储m项，大大降低了参数量。

相比One-hot Full Embedding，编码部分变为：$E(s)=\mathbf{b}=\{0,1{\}}^m$，然后还是通过lookup查找得到embedding：$\mathbf{e}=W^T\mathbf{b}$

但是这也会带来哈希冲突的问题：多个id共享一个embedding，肯定会confuse模型。

解决方法可以用k个不同的哈希函数$\left\{H^{(1)},H^{(2)},\dots H^{(k)}\right\}$，按照上述方法生成k个one-hot编码：$\left\{{\mathbf{b}}^{(1)},{\mathbf{b}}^{(2)},\dots {\mathbf{b}}^{(k)}\right\}$，即一个特征分别落到了k个桶中，分别从embedding table取出向量，并且把最后的结果concat到一起或者做avg-pooling。

这种做法相当于利用特征组合构造独特性。 文章其实用NN把这句话做的更深！

Deep Hash Embeddings

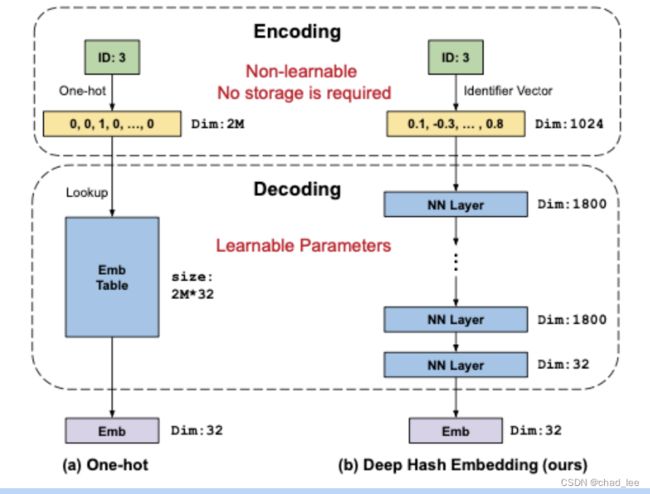
文章把 id --> emb 这个过程建模成 encoding- decoding的过程，one-hot的过程xxxx。

DHE是先通过多个(k=1024个)哈希函数将特征表示为稠密的Identifier vector, 解码阶段通过多层神经网络得到该特征的唯一表示。

Encoding阶段

文章首先提出如何衡量一个好的encoding function：

• 独特性：编码对每个特征值都应该是唯一的；
• 同质性：有唯一性并不足够,相似特征编码后也要足够相似.比如二进制编码,8(1000)和9(1001)就比8(1000)和7(0111)看着相似,这就会给模型带来困扰,误导后面的decoding过程.
• 高维：encode函数要让decode函数容易区分不同的特征值。由于高维空间通常被认为是更可分离的，而且信息包含的更多；但是one-hot的编码其实太稀疏对后续的decode其实不太容易；
• 高香农熵：香农熵测量每一维度包含的信息量，高香农熵意味着编码过程中信息损失很小（避免在一些维度所有特征值都一样），希望最大化每个维度上的熵来有效利用所有维度。例如，one-hot编码在每个维度上的熵都很低，因为任何维度上对于大多数特征值来说都是0。因此，one-hot编码需要极高的维度（即），效率非常低。

DHE运用 k 个哈希函数把每个类别特征（id）映射为一个 k 维的稠密向量。

具体的，每个哈希函数 $H^{(i)}$ 都将一个正整数 $\mathbb{N}$ 映射到 $\{1,2,\dots \mathrm{m}\}$, 本实验中取 $m=1e6$ 。因此， $k$ 个哈希函数就把1个正整数id $\mathbb{N}$ 映射成了 $k$ 维的向量 $E^{\prime }(s)=\left[H^{(1)}(s),H^{(2)}(s),\dots ,H^{(k)}(s)\right]$ ，向量中的每个元素都取自 $\{1,2,\dots \mathrm{m}\}$ 。实验中取 $\mathrm{k}=1024$。

然而，直接用上面得到的编码表示送入神经网络是不合适的，因此作者进行了两个变换操作来保证数值稳定性：

• 均匀分布（Uniform Distribution）：把 $E^{\prime }(s)$ 中的每个值映射到[-1,1]之间

• 高斯分布（Gaussian Distribution）：把经过均匀分布后的向量转化为高斯分布 $N(0,1)$。

作者说，这里是受到GAN网络的启发，用服从高斯分布的随机变量做GAN网络的输入。实验结果显示这二者相似，作者就默认用均匀分布。

作者说经过理论分析这样设计的encoding满足上面的4个条件，然后把理论分析放在附录，然后在附录写了一些莫名其妙的东西，直觉上感觉这种方法并不符合同质性：

Decoding

decoding阶段就是用多层神经网络，依赖的是“多层NN可以拟合任何函数”。但是由于参数量比embedding table少了很多，所以模型会欠拟合。

为了解决这一点作者引入MISH激活函数$f(x)=x\cdot \tanh \left(\ln \left(1+e^x\right)\right)$代替ReLU，引入更多的非线性从而提升表达能力：

同时还加了BN这种优化技巧。

加入辅助信息以增强泛化性(解决OOV问题)

作者也觉得他这种方法不能满足同质性Equal Similarity，因此提出对于物品ID、用户ID，在encode之后再拼接上属性（年龄、性别、品牌等），然后在输入到DHE中解码，为最终生成的embedding补充同质性。

所以附录里证明了个寂寞。

实验结果

• DHE取得了和one-hot相近的性能，但参数了极大的减小了。
• 其他方法虽然减小了参数量，但性能都下降了