python实现综合评价模型TOPSIS

原文：https://mp.weixin.qq.com/s/J9fZQ8T9TR1Ed7taPGYYjw

1 TOPSIS简介

有关综合评价的方法有多种， 根据赋权方法不同主要有两类：一类是主观赋值法， 如指数法、层次分析法、模糊综合评价法等；另一类是客观赋值法， 如因子分析法、TOPSIS 法、人工神经网络法等。

本文主要介绍 TOPSIS 法。TOPSIS( Technique for Order Preference by Similarity to an Ideal Solution) 法， 即理想解法， 由 C.L.Hwang 和 K.Yoon 于 1981 年首次提出， 可用于效益评价、决策、管理等多个领域。

该方法根据各测评对象与理想目标的接近程度进行排序，在现有研究对象中进行相对优劣评价。

其基本原理是通过测度各评价对象与最优解、最劣解的距离来进行排序， 若评价对象最靠近最优解同时又最远离最劣解，则为最优；否则不是最优。

TOPSIS 法的主要评价步骤(极大型指标)如下：

根据接近程度大小即$C_i(0<=C_i<=1)$的大小进行排序，$C_i$值越大，表明评价单元越接近理想状态， 评价结果越好。

也可以根据公式得出，当$S_i^{+}$越大时，$Z_{ij}$越接近最大值。

该方法对数据分布及样本含量没有严格限制，数据计算简单易行。

针对上述步骤中，在得到指标矩阵时，还需根据目标进行指标正向化，然后再归一化处理。接下来具体讲解指标正向化。

2 指标正向化方法

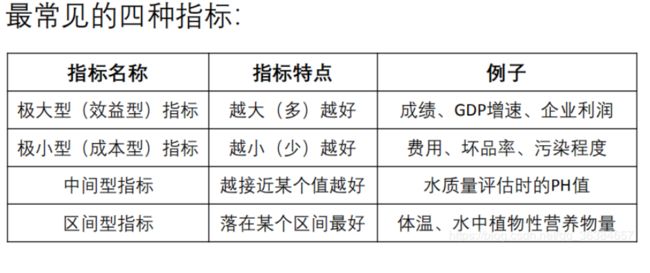
1）极大型指标

越高（大）越好，这样的指标称为极大型指标（效益型指标）。

$$x=\frac{x-x_{min}}{x_{max}-x_{min}}$$

如学习成绩：

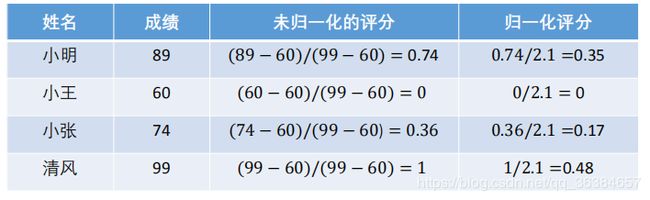
2）极小型指标

越少（越小）越好，这样的指标称为极小型指标（成本型指标）。

对于这类指标，正常是转为将所有的指标转化为极大型指标，即指标正向化。

极小型指标转换为极大型指标的公式：

$$x_{max}-x$$

如果所有极小型指标的数据都为整数，那么也可以用如下公式进行转换：

$$\frac{1}{x}$$

下图显示了将“与人争吵的次数”这一极小型指标转化为极大型指标的结果：

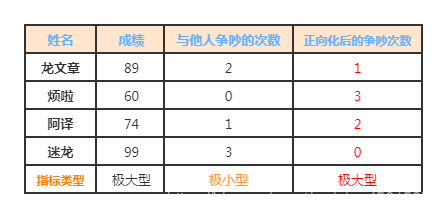
3）中间型指标

中间型指标的特点：指标的值既不要太大也不要太小，取某个特定的值最好。

做法也是转化为极大型指标。

设$\{x_i\}$是一组中间型指标序列，且最佳数值为$x_{best}$，则正向化公式：

$$M=\max \{x_i-x_{best}\},\widetilde{x_i}=1-\frac{|x_i-x_{best}|}{M}$$

例如： 水质量评估 PH 值指标正向化，PH值取7时水质最好：

4）区间型指标

区间型指标：指标落在某个区间内最好。

设$x_i$是一组区间型指标序列，且最佳的区间为[a,b]，那么正向化的公式如下：

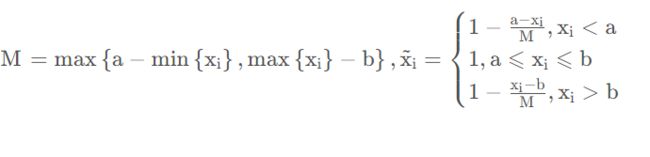
例如： 例如人的体温在36摄氏度~37摄氏度这个区间内最好：

3 python实现

TOPSIS一般结合熵权法使用。

import pandas as pd
import numpy as np

#逆向指标标准化
def normalization1(data):
    _range = np.max(data) - np.min(data)
    return (data - np.min(data)) / _range

#正向指标标准化
def normalization2(data):
    _range = np.max(data) - np.min(data)
    return (np.max(data) - data) / _range

#熵权法计算权重
def entropyWeight(data):
    P = np.array(data)
    # 计算熵值
    E = np.nansum(-P * np.log(P) / np.log(len(data)), axis=0)
    # 计算权系数
    return (1 - E) / (1 - E).sum()

def topsis(data, weight=None):  
    
    # 权重
    weight = entropyWeight(data) if weight is None else np.array(weight)
    
    # 最优最劣方案
    Z = pd.DataFrame([(data*weight.T).min(), (data*weight.T).max()], index=['负理想解', '正理想解'])
    #Z = pd.DataFrame([data.min(), data.max()], index=['负理想解', '正理想解'])
    
    # 距离
    Result = data.copy()
    #Result['正理想解'] = np.sqrt(((data - Z.loc['正理想解']) ** 2 * weight).sum(axis=1))
    #Result['负理想解'] = np.sqrt(((data - Z.loc['负理想解']) ** 2 * weight).sum(axis=1))
    Result['正理想解'] = np.sqrt(((weight*data - Z.loc['正理想解']) ** 2 ).sum(axis=1))
    Result['负理想解'] = np.sqrt(((weight*data - Z.loc['负理想解']) ** 2 ).sum(axis=1))

    # 综合得分指数
    Result['综合得分指数'] = Result['负理想解'] / (Result['负理想解'] + Result['正理想解'])
    Result['排序'] = Result.rank(ascending=False)['综合得分指数']

    return Result, Z, weight

if __name__=='__main__':
    data = pd.read_csv('testdata.csv',sep = ',',encoding='gbk',header=None)
    data1 = data.copy()
    data1[0] = normalization1(data1[0])
    data1[1] = normalization1(data1[1])
    data1[2] = normalization1(data1[2])
    data1[3] = normalization1(data1[3])
    [result,z1,weight] = topsis(data1)

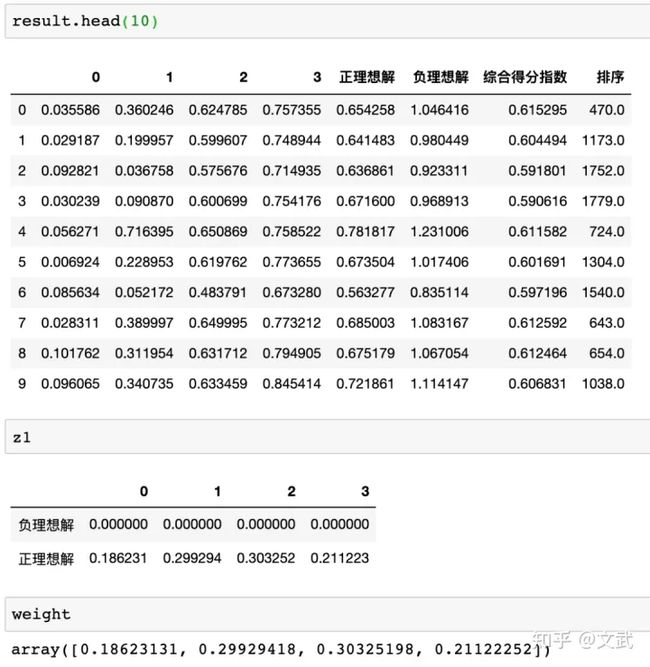
最终得到的评分结果（部分）、正负理想解和权重如下：

参考：
https://blog.csdn.net/qq_36384657/article/details/98188769
https://zhuanlan.zhihu.com/p/345513712
https://blog.csdn.net/qq_36384657/article/details/98188769