R语言基本用法(主要为时间序列分析方面)
前言
本文是我个人对于之前学习的R语言的一个复习,也是给同样学习R语言的同学们看一看,主要目的是便于理解和使用,文中并没有过多对于函数原理介绍,主要是公式何处应用和怎样应用,如果对于具体的原理感兴趣,可以查阅书籍或自行网上搜索。
R语言下载
如果您已经下载完毕,尽管跳过这一环节,毕竟这玩意没啥好说的。
首先是登陆CRAN的官网
http://cran.r-project.org
http://cran.r-project.org
这里试了两个方法输入网站。(毕竟我也第一次发布文章弄网站,不太懂,理论上来说第一个出现的网站是链接,第二个是可以像其他文章里的代码那样直接复制的,要是不行的话,就只能手动输入了)
接下来就很简单了,右侧的Download and Install R里根据自己电脑的操作系统进行选择
然后在网页里选择install R for the first time(第一次安装R)
最后选择最大的一行字Download R 4.1.2 for Windows (我觉得我在说废话,只要找到网页谁都会下(笑))。
再说一句废话,下载时注意不要把所有东西都扔到C盘。
R的正式使用
程序包的下载
下载完毕,这时候我们其实就已经可以使用R了,但我们首先需要学会程序包的下载。
程序包可以帮我们省很多事,本文的各种操作也需要不同程序包的支持。
进我文章的应该都是我一样的萌新,应该没有自己搞的大佬吧。真有大佬的话,如果大佬腿上缺个挂件,麻烦评论区说一声,我麻溜的去抱大腿。
R语言有多种下载与安装程序包的方式,这里说一下最简单的两种。毕竟我也只会两种
- 通过菜单栏选项下载安装
首先打开R进入操作系统。如下图所示

打开“程序包”,里面有个明晃晃的“安装程序包”,点开它,接下来选择镜像站。这个随便选就行了,我打字的时候国内九个选择,选哪个没啥建议,不保留工作映像下次打开还能选。
选完镜像站,它会弹出来如下窗口(可能会卡一下)

这里我们下载一下tseries,按字母排序找到tseries,点击确定,下载完成。(如果下不了可能网络状况不太好,如果网络没问题那就换个镜像站)
2. 直接输入指令下载安装
直接在对话窗口输入安装指令
install.packages("tserise")
然后回车键。如果此时还没选择镜像站,那系统会自动弹出选择界面。
程序包的使用
这没啥好说的,library()调用,拿刚才搞的tseries举例
library(tseries)
R语言基本规则
R可以在打开的控制台编辑,但每次回车,输入内容就会立刻运行,如果是一系列命令中间试图看一下运行结果,那之前的命令很容易就被顶到看不到的地方去了。如果不喜欢这样的模式,可以在“文件”中打开“新建程序脚本”,此时的命令回车只会换行而不会立刻执行,需要执行的时候,选择要执行的区域,(注意,在程序脚本中你必须鼠标手动选中所有你打算运行的程序,否则只会运行编辑位置所在的那一行)然后选择“编辑”里的“运行当前行或所选代码”即可。
输入的规则
输入函数错误时,R会直接提示你没有相应函数。但如果你输入的不全,比如,当输入sum(1,2,3时,按下回车键,R会自动出现一个红色的“+”号,这意味着你没有完成这个命令,话没说完,这时可以在+后面直接继续编辑,如果再按下回车,它就会继续提醒你“+”号,直到你加上右括号将其完善才结束。(sum为求和,这个后面还会说)
操作如图:

但如果你的错误R自己不认识,那就只能用万能的esc退出这条指令了。当你看到你的输入行的开头变成>,那就能输入新指令了。
赋值命令的写法
赋值永远是系统使用重要的一环。和其他软件赋值使用的“=”不同,R语言的标准写法是使用“<-”或者“->”表示赋值,具体情况拿例子更好解释。
例如,我们要完成x=3
那我们可以输入“x<-3”,也可以输入“3->x”,这两个作用是一样的。
给x赋完值我们可以直接输入x来看看x现在代表着什么。

要注意的两个小点
R本身区分大小写,x和X在R里是两个东西。
R的控制台上无法直接通过鼠标点击改变编辑位置,比如你输入library(tserise)你发现最后的e和s位置错了,你鼠标选中“se”,点击删除键,这时被删除的是右括号。只有键盘上的左右方向键才能改动编辑位置。上键则会显示上一条命令。
常用运算符号和常用函数表达式
常用运算符号
假装是竖线那个是我不知道怎么搞,直接加竖线就会把前面那个也分割开了,凑合一下看吧。
| 运算符 | 描述 |
|---|---|
| + | 加 |
| - | 减 |
| * | 乘 |
| / | 除 |
| ^ | 幂次运算 |
| < | 小于 |
| <= | 小于等于 |
| > | 大于 |
| >= | 大于等于 |
| == | 严格等于 |
| != | 不等于 |
| !x | 非x |
| x(假装是竖线)y | x或y |
| x&y | x和y |
常用函数
| 函数 | 描述 |
|---|---|
| abs(x) | 绝对值 |
| sqrt(x) | 平方根 |
| sin(x) | 正弦 |
| cos(x) | 余弦 |
| tan(x) | 正切 |
| log(x) | 自然对数 |
| log(x,base=n) | 以n为底求对数 |
| exp(x) | 指数 |
| mean(x) | 均值 |
| sum(x) | 求和 |
| range(x) | 值域 |
| diff(x) | 差分运算 |
| diff(x,n) | n步差分 |
| lag(x) | 延迟运算 |
| min(x) | 最小值 |
| max(x) | 最大值 |
| set.seed(n) | 产生以n为基数的随机种子 |
| runif(n) | 产生n个(0,1)区间的均匀分布随机数 |
| median(x) | 中位数 |
| var(x) | 方差 |
| sd(x) | 标准差 |
| quantile(x,probs) | 分位数 |
| rnorm(n) | 产生n个标准正态分布随机数 |
| pnorm(x) | 计算标准正态分布的分位点 |
| qnorm(q) | 标准正态分布函数为q的分位数 |
生成时间序列数据
直接录入
直接录入在数据比较少和练习的时候最好用,但数据一多就不行了,总不能几百几千行的数据一个个敲吧,那不得累死。
行输入
行输入是最常见的一种输入,直接说太耗费口舌,我们用例子来说明。我先放出输入和结果,然后再解释。
输入
>price<-c(101,82,66,35,31,7)
>price<-ts(price,start=c(2005,1),frequency=12)
>price
结果:

结果的第一行是月份的缩写,从一月开始到六月,下面一行是该月对应的数据。
首先简单说明每一行都在干什么:
第一行是往“price”这个变量里注入数据
第二行是为变量加上对应的横坐标
第三行是输出“price”看看现在是什么样子
然后具体说明一下:
第一行,c是指调用c函数,简单的说,c里的东西会被依次赋值给前面的变量。
第二行,添加时间横坐标的格式为
ts(变量名,start=c(年份,月份),frequency=)。
变量名不用太多解释。
start是开始的年份加上开始的月份,这个和后面的frequency也有关系。
frequency是每年读入数据的频率,比如半年半年的搞,frequency就等于2,一个季度一个季度的搞,frequency就等于4,一个月一个月的搞,frequency就等于12,一天一天的搞,frequency就等于365。
第三行,输出做好的变量“price”。
列输入
列输入ts操作和横坐标一样,我们只说一说改变的第一行。
列输入的模式是
>price<-scan
1:101
2:82
3:66
4:35
5:31
6:7
7:
具体来说的话,就是这样的:
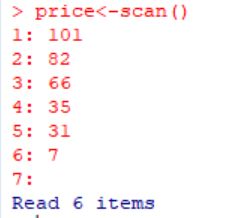
这里输入“price<-scan”后,按下回车键,后面的“1:”“2:”等都是R自己给你准备好的,直接往里输入数据就好了。输完一个数据按一下回车,数据输完后,在空白行回车,就表示输入完毕了,比如这里要输入六个数据,那在第七个数据该写的地方直接回车就好了。
外部数据导入(read.table)
这是最简单快速且有效的输入方式了,尤其是对于txt和csv格式,拿来就能直接用。txt文本不用说,csv是表格的一种格式,后缀不是csv的表格转换一般另存为换个格式就行了。
格式为
x<-read.table("文件地址",sep="文件的类型",header=)
注意:我这里的所有引号都是不能省略的。
文件地址,就是你要的数据的具体地址,比如“E:\R\file1.csv”.(在这里windows电脑在输入地址时应该是要把单斜线都变成变成双斜线,如果还不行的话把“\”变成“/”)。
由于R本身的一些原因,引用可能无法完成,接下来插播一条重要消息,也是一个重要的解决方法
插播一条重要消息(无法读取的解决方法)
有的人在正确的输入格式后,还是无法读取文件,下面给出这个问题的主要解决方法。
先输入
getwd()
确认一下当前的工作目录,(R只能对于放在他工作目录下的文件进行操作,比如如果工作目录是E盘,数据文件在C盘,就算文件地址没问题,大概率是无法读取的)如果工作目录并不是我们想的位置,不要慌,我们换一个。
setwd("想设定的地址")
比如:我想把工作目录变成E盘里叫“R”的文件夹,那么,我输入
setwd("E:\\R")
这样它的工作目录就变成了E盘里叫“R”的文件了。
回到刚才的问题
回到刚才的问题,为防止遗忘或观感差,我再写一遍:
x<-read.table("文件地址",sep="文件的类型",header=)
文件地址,就是你要的数据的具体地址,比如“E:\R\file1.csv”.
sep=“文件的类型”,sep等于什么,这得看你存数据用的是什么文件,如果是txt文件,那就是sep="\t",如果是csv文件,那就是sep=","。比如我刚才举例的是csv文件,那就是sep=","
header=,有两个选择,header=T或者header=F。T是第一行包含变量名,也就是第一行是不是像是yield,生产总值这样的介绍性文字,如果是,那就用T。但如果第一行就是要用的数据,那就用"F"。
插一句嘴,尽量还是在第一行写上具体的名称比如yield(收益率)之类的 ,这样操作起来方便,之后也能直接调用这一列。
把我上面的举例结合起来
x<-read.table("E:\\R\\file1.csv",sep=",",header=T)
结果太长就不演示了,只放出最开始的一小段截图。

注:header=T保留的就是year,yield,ln_yield这行的东西。
接下来一点,如何使用这里面的数据呢?
拿我的举例,直接输入yield是无法输出的,应该用
> 数据框$变量名
的方法,比如我的变量叫x,想导出yield的数据看一看,那就输入x$yield,就能看到yield这一列的所有数据了。
数据的处理
现在距离使用就差临门一脚了,只要知道如何对数据进行初步处理,那就可以开始真正的使用了。
变换
最简单最基础的数据处理手段,拿例子来说明
y<-log(x$yield)
给y赋值的时候把yield的数据全部变成原来的对数,这样的操作就叫变换。
子集(使用subset)
子集其实就是从原来的数据里拿出一部分。还是拿例子说明,毕竟例子最直观
z<-subset(x,year>1925,select=yield)
这句话作用是将1925年之前的数据剔除并只保留yield这一列。
x是变量名
year>1925,限定x里year列的数据大于1925
select=yield,往z里输入yield这一列的数据。结果部分截图如下:

把缺失的数据用插值填充(approx与spline)
有时候处理数据时,我们不得不面对有缺少数据的情况,这时候,缺失的数据地方会显示“NA”,意思是“not available”,无法获得。一旦出现这玩意,就算是只有一个R都得罢工,怎么处理呢?用插值补全数据,插值方法很多,这里暂时不一个个的说,不过常用的两个方法,线性插值法和样条插值法都能用zoo程序包提供,那就先下一个
zoo程序包,下载和使用程序包的方法开头就提到了
install.packages("zoo")
library(zoo)
接下来我们还是用个好懂的方法进行解释,举例子。
a<-c(1:7)
a[4]<-NA
a
y1<-na.approx(a)
y1
y2<-na.spline(a)
y2
前三行是人为做出一个缺失值并查看。
后面是分别利用线性插值法和样条插值法补全数据。不需要深入了解,会用即可。
数据导出(write.table)
得到了我们想要的数据,接下来当然是要数据导出来,导出来的格式为
> write.table(变量名,file="想存储的位置加导出的文件名",sep="存储的格式",row.names=F)
变量名也就是我们准备好的变量
file=的是应该存储的位置,但是我们要注意,在这里,我们存储的位置中间并不是正常位置的“\”而是“/”,举个例子,我要存到E盘的R文件里,并且它要叫“yield”,csv格式。那我就应该输入file=“E:/R/yield.csv”
sep=还是和上面一样,如果是txt文件,那就是sep="\t",如果是csv文件,那就是sep=","。如果你觉得这句话很熟悉,没错,这就是我直接把上面那句话复制黏贴的。
row.names=,这是看有没有行变量名,这里并没有行变量名,那就是row.names=F
接下来结合起来,做成一个例子:(这个例子与前面例子的连接的)
> ln_yield<-log(x$yield)
> x_new<-data.frame(x,ln_yield)
> write.table(x_new,file="E:/R/yield.csv",sep=",",row.names=F)
第一行把yield的数据做对数运算并赋值给ln_yield
第二行出现了一个新东西,data.frame,它的作用是把后面括号里的东西合在一起。也就是说,在这一行里,我们把x和新做出来的ln_yield合在了一起。
为了直观说明,我截一下最后的结果图(我之前里面就有一列ln_yield,所以它自己变成了ln_yield.1)
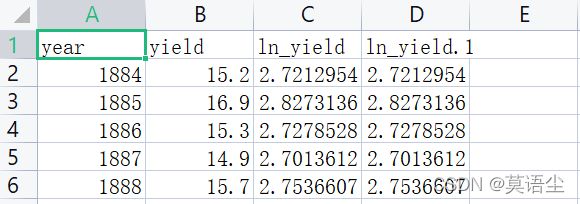
第三行是我们刚才说到的导出为文件。
write.table(x_new,file=“E:/R/yield.csv”,sep=",",row.names=F)
这里的x_new是我上面新赋值的变量
file="E:/R/yield.csv"在E盘的R文件夹创一个叫yield.csv的表格。这里把正常目录里的\换成/,否则可以运行,但不会出现文件。
这里和工作目录不一样,一个/就够了,虽然两个/效果也一样,但没必要多费工夫。
另外一点,这里存放位置不再受工作目录影响,除了C盘应该都能直接做一个。
sep=","这个应该不用说了
row.names=F,我没对每个行变量命名,所以是F。
画图(plot)
最简单版本的画图
plot(变量名)
没啥好说的,举个例子
y<-c(1,2,3,4,5)
y<-ts(y,start=2022)
plot(y)
相信都明白这三行是什么意思,按下回车它会出来一个弹窗,弹窗内容如下

但其实plot没有这么简单,实际上它的完全体很长:
plot(y,type="",lty=,pch=,lwd=,col=,main="",xlab="",ylab="",xlim=,ylim=)
不过使用的时候只要不用,那就不用提,比如刚才我除了指定变量名,后面的一个都不要,所以后面的一长串我都没打。不过为了美观,掌握这些还是比较需要的。一个个来说。
y是变量名
点线的类型(type)
type是控制点和线的有六种,p,只有点,l,只有线,b,点连线(线不穿过点),o,和b差不多,但是线穿过点,h,悬垂线(山洞顶的钟乳石那样的),s,阶梯线(顾名思义)
点的形状(pch)
pch是控制点的样子的,上面如果选择“l”那就不存在这个问题了,pch=对应的是数字,比如pch=2,pch=17这样的。对应的图片如下

线的类型(lty)
线的宽度(lwd)
lwd则是用来设置线的宽度的,lwd=1的时候是默认的宽度,lwd=k的时候则表示是默认宽度的k倍,lwd=-k的时候,则表示是默认宽度的1/k倍。
点线颜色(col)
col可以设置点线的颜色两种选择方式,一种是直接col=数字,另一种是col=“颜色的英语”,据说R语言有657个颜色,但我个人的看法来说,颜色的细微差别太难分清了,记住基本的几个就够了。

添加名称(main,xlab,ylab)
main 是用来添加标题的,xlab是添加横坐标名称,ylab是添加纵坐标名称。简单的说,如果打算把图像叫“某某年到某某年生产变化”,横坐标是年份,纵坐标是生产值,那这一部分就能写成
main="某某年到某某年生产变化",xlab="年份",ylab="生产值"
选取范围(xlim,ylim)
最后的xlim和ylim是分别指定x轴和y轴输出的范围,比如xlim=c(1,10)这就是输出图像只输出x在1-10时的图像。
添加参考线(abline)
参考线这里介绍两种,垂线和水平线,两种线都由abline调动
abline(v=,lty=)#垂线
abline(h=,lty=)#水平线
例子:在x=4的时候画个虚垂线
abline(v=4,lty=2)
在x=4和8的时候画个虚垂线
abline(v=c(4,8),lty=2)
水平线同理
自相关图(acf)
自相关系数是一个很重要的数据,这里不展开说它具体的原理的,只说它的形式和简单的看图方法。
acf(变量名,lag=延迟阶数)
一般直接acf(变量名)就行了,延迟阶数的话,看图说明好说明一点。
看图方式我们先看这个图:
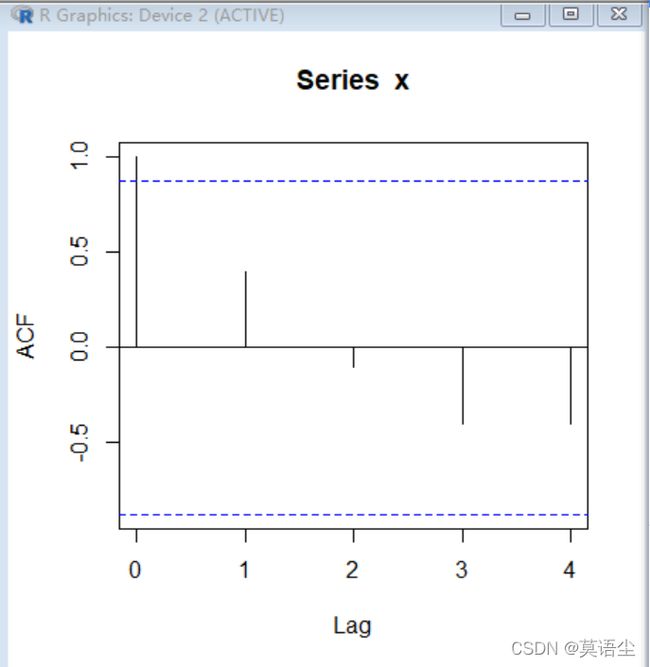
后面的竖线只要在上下两条虚线内,一般可以看作随机性强,如果有某一个竖线超过了虚线,但后面不再超出虚线,那么这个竖线是第几个,那么它就是输出滞后几阶的白噪声检验统计量,这个数字就是它的延迟阶数。
而像我图里这样的,自身减少的很有规律,可以视为有单调趋势。如果自相关系数一直在某一侧,这也是单调趋势,如果他自己还呈现出正弦函数一样的图像,那就代表他自己还有周期性,当然我这里是随便输的几个数,太少了没法具体判断。
偏自相关图(pacf)
和自相关系数一样是重要的一环,但原理不再赘述,使用方法和acf一样。
pacf(变量名,lag=延迟阶数)
前置工作终于全部准备完毕。经过前面漫长的介绍,快车终于要发动了。从现在开始,真正要开始应用了。
纯随机序列
纯随机序列是最理想的序列,简单的说,如果有一串数据,每个数据相互之间都是随机且没有关联,而且数值一直在0上下波动,那这就是纯随机序列。
纯随机序列也叫白噪声序列,因为最初人们发现白光有这样的性质。当然,其实不需要知道它命名的来历,知道它还叫白噪声序列就行了,因为后面我们还得经常提到它。
正态分布随机数生成(rnorm)
先直接上标准式子
rnorm(n=生成随机数的个数,mean=均值,sd=标准差)
n是打算生成的随机数的个数
mean=的是均值,也就是要围绕什么数波动,不输入默认为0
sd=的是标准差,也就是波动大小,不输入默认为1
也能简化为rnorm(生成随机数的个数,均值,标准差)
如果不用特殊设置均值和标准差,也可以直接rnorm(随机数个数)
纯随机性检验(Box.test)
纯随机性检验的目的是判断数据是否相互之间没有联系,是不是白噪声序列。
式子如下:
Box.test(x,type=,lag=)
x指变量名
type是检验统计量类型,白噪声检验有两个检验统计量,Q检验统计量和LB检验统计量,这里不展开说具体的原理,等会说完怎么看,会看即可。
type=’‘Box-Pierce’’,输出白噪声检验的Q统计量,这也是默认的选择
type=’‘Ljung-Box’’,输出白噪声的LB统计量
lag,延迟阶数,暂时用不太到。默认是滞后1阶的白噪声检验统计量。
举个例子,不规定其他数值,对变量x进行白噪声检验
Box.test(x)
最常见的延迟六阶和延迟十二阶:
Box.test(x,lag=6)
Box.test(x,lag=12)
结果长这样
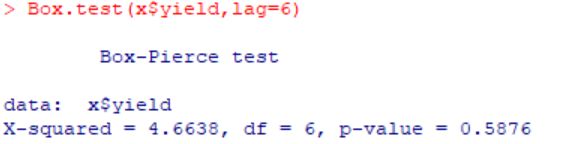
这张图怎么看呢?其实不部分都不用管,看最后p-value的数值就行了,它大于0.05(置信水平)则认为不能拒绝原假设,小于0.05则认为小概率事件发生,推翻原假设,拒绝原假设。
补充,循环语句(以及for对于随机性检验的加强)
相当经典的循环语句,我目前所知的语言都有for循环,相互之间的格式也大致相同,R里的for循环语句是
for(x, in, n1:n2) state
x是循环的变量名,一般用i比较多
in 是单纯的单词
n1:n2是循环的取值区间
state是要循环的条件
举个例子,刚才上面的那一段,同时输出延迟6阶和延迟12阶的结果。
for(i in 1:2) print(Box.test(x$yield,lag=6*i))
这样应该就直观多了。我们经常使用的检验也是这种6阶和12阶一起出来的检验方式
ARMA模型
ARMA是一个很有用的模型,这里不仔细说明它的运行原理,只说用法。在我们将模型(比如![]()
这样的模型。代入ARMA的拟合函数里运行后,我们继续在R里把图画出来,(无论画什么图都行,前面说的直接拟合plot就行,这里也能用plot的进阶版ts.plot,时间序列坐标轴,用法一样。或者看情况使用自相关图acf,随便选)
AR模型判别(arima.sim和filter)
arima.sim的用法
arima和arma其实是一个模型,这个模型的缺陷在于只能拟合平稳的序列。
在这里,拿刚才的例子
![]()
我们用ARMA的目的就是要判断这东西的平稳性
老规矩,先列出来原来的样子
arima.sim(n,list(ar=,ma=,order=),sd=)
n是要列出多少的序列,比如我们可以输入100,搞100个数
list里面的东西是指定具体的模型,
单一个AR是指拟合AR模型,它等于自回归系数,比如我们举的例子里,ar=0.8,如果是多个数,那就是ar=c(1,2,3)这样的形式。
单一个MA是指拟合MA模型,要给出移动平均数,这个我们等接下来的MA模型再说。
如果AR和MA同时存在,而没有order,那就是ARMA模型
如果三者都齐活了,那就是最终的ARIMA模型了,在这里,order=c(p,d,q),p为自回归阶数,d为差分阶数,q为移动平均阶数。这里不急着展开,后面还会说,现在我们先解决AR模型。
sd是指定序列的标准差,不特殊指定则默认为1。
接下来是命令图和结果图展示
命令图:
![]()
结果图:

这样的图也在平稳的范畴内,只要后面的不是绝对值越来越大基本上都能这么认为,接下来的filter里我们搞个不平稳的。
filter的用法
filter和arima.sim不同的地方是filter能直接拟合AR和MA序列而不用在乎它是否平稳
还是一样先举例子
![]()
然后说式子
filter(e,filter=,method=,circular=)
e是变量名,没错,我们如果用filter,那我们还需要构造变量,比如 e<-rnorm(100)。这个函数在上面说了,记不清的可以瞥一眼目录。
filter=是来指定模型系数的,对于AR模型那就是filter=c(,)这个样子,对于MA模型那就是c(1,-,-)(后面的横线是负数的意思,在原数据的基础上取负值)
method=指定是用AR模型还是MA模型如果是method="recursive"则为AR模型,如果是method="convolution"则为MA模型
circular=是拟合MA模型专用的选项,circular=T可以避免NA出现。
说着挺乱,那我们例子说话
e<-rnorm(100)
x2<-filter(e,filter=-1.1,method="recursive")
ts.plot(x2)
结果为
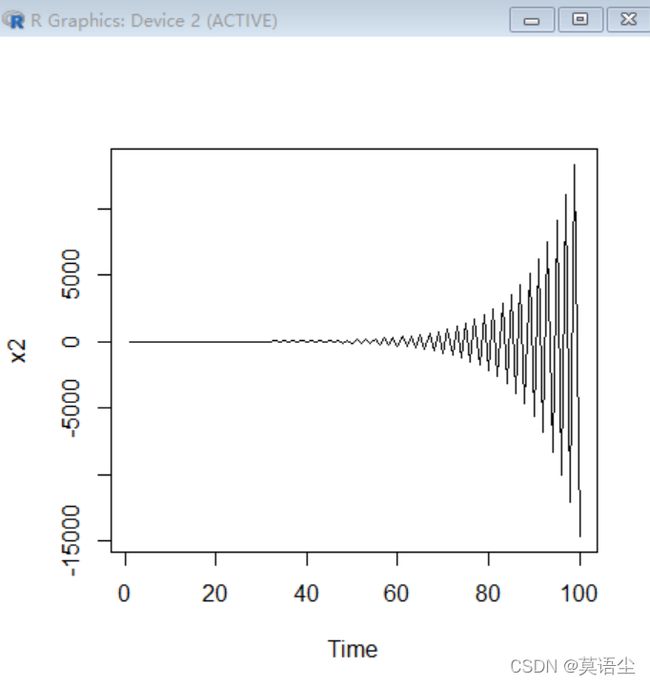
这个样子的图像就是典型的非平稳。
当然,我们也能用另外的方法判别是否平稳,比如在AR模型中,如果有一个自相关系数,比如我们第一个例子里的0.8,它的绝对值小于1,然后我们就能得出结论,它平稳。对于有两个系数的,比如这个
![]()
这里第二个系数绝对值为0.5小于1,两个系数相加等于0.5小于1,第二个系数减第一个系数等于-1.5小于1,所以这式子也平稳,这三个条件只要有一个不满足,那就是非平稳。
平稳的AR模型,它的后面的自相关系数不会超过上下两个虚线,看例子,还是第一个式子,我们把数取到1000
x1=arima.sim(n=1000,list(ar=0.8))
acf(x1)
MA模型判别(和AR其实一样)
和AR内容一样,举个例子就行了
arima.sim(n,list(ma=))
x3=arima.sim(n=1000,list(ma=c(-4/5,16/25)))
让我们看看它的自相关系数图

对于AR的自相关系数图,开始的时候有几条竖线超过虚线那么就是几阶截尾,但对于MA来说,第一条竖线一定会超出虚线,需要将超出虚线的竖线个数减一,比如这张图就是MA的二阶截尾。
其实AR和MA大部分操作是一样的,只是在细枝末节上有细微差别。但是我们根据看他们的自相关系数图和偏自相关系数图可以得到要调查的式子属什么模型:
| 模型 | 自相关系数 | 偏自相关系数 |
|---|---|---|
| AR( p ) | 拖尾 | p阶截尾 |
| MA( q ) | p阶截尾 | 拖尾 |
| ARMA (p,q) | 拖尾 | 拖尾 |
自动定阶(auto.arima)
其实光靠我们的肉眼,有时很容易出现失误,尤其是随机数的有一定的波动性,可能导致我们看着并不明显。这时候我们就要取出我们的一个法宝:auto.arima
但动用这个法宝是有前提的,必须先调动zoo和forecast两个程序包。
原式如下:
auto.arima(x,max.p=,max.q=,ic=)
接下来要说的,除了x要记住,其他的稍微了解就可以,大多数时候我们直接auto.arima(x)就可以了
x是需要定阶的序列名
max.p是自相关系数的最高阶数,不指定则为5
max.q是移动平均系数的最高阶数,不指定也为5
ic指定信息量的准则,有三个准则:“aicc”,“aic"和"bic”,系统默认为AIC准则。
参数估计(就是把数变成式子,arima)
我们现在可以对于序列分散的数分析,也可以对于ARMA模型的式子进行分析,那我们有没有办法把这两样东西合二为一呢?还真有。
arima(x,order=,include.mean=,method=)
我们可以在自动定阶完成的基础上,靠它得出模型的样子。
x是序列名
order=是指定模型阶数,和之前那几个一样order=c(p,d,q),p为自回归阶数,d为差分阶数,q为移动平均阶数。p和q我们可以从刚说的自动定阶来得到,至于差分,暂时没差分,d现在当0就可以了。
include.mean=是是否需要拟合常数项,include.mean=T需要拟合常数项,这也是默认项,include.mean=F不需要拟合常数项。
method=是指定参数估计要用啥办法
method="CSS-ML"是条件最小二乘估计和极大似然估计混合方法,method="ML"是极大似然估计,method="CSS"是条件最小二乘估计。
拿个例子说结果更好理解一些:
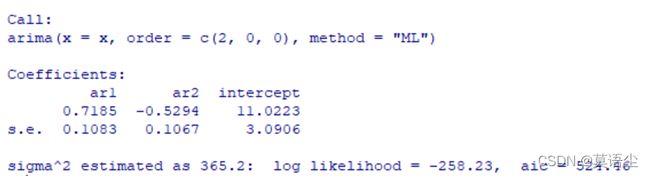
这是结果的全图,我们只需要注意一小部分就行了


靠它我们可以得到式子:
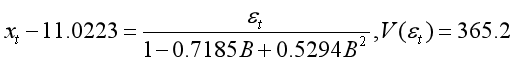
或者可以等价的进一步写成
![]()
(下面式子8.9383大致能看成11.0223*(1-0.7185+0.5294),当然后面肯定和它有误差,这和保留位数有点关系)
模型的显著性检验(用白噪声检验残差)
模型构建完毕,我们需要对于模型进行分析,我们要的是什么模型呢?残差要在0附近上下波动,换个我们已经见过的词,白噪声序列。只要残差满足白噪声,那说明我们的模型有效。这里我们要说到一个词residual,利用它我们可以得到残差,并以此来进行白噪声检验
以例子来说明
for(i in 1:2) print(Box.test(x.fit$residual,lag=6*i))
在变量里不需要有residual这一列,residual是用来算变量的残差的。
结果的看法和白噪声是一样的(就是一个东西)
参数的显著性检验(pt)
参数的显著性检验主要目的是判断答案是否非零,格式为:
pt(t,df=,lower.tail=)
t是t统计量的值,这个过会儿举例子就好说了
df是自由度,这个不用多说
lower.tail是确定计算概率的方向,这个和t有关,如果t是正数,那么lower.tail=F,如果t是负数,那么lower.tail=T。
那刚才我们的那个图举例

这里检验第一个系数需要的t统计量就是0.7185/0.1083,分子分母本来都是正数,所以lower.tail=F,式子为
t1<-0.7185/0.1083
pt(t1,df=56,lower.tail=F)
第二个系数的t统计量为0.5294/0.1067(不加正负号,算绝对值),分子本来是负数分母本来是正数,所以lower.tail=T
t2<-0.5294/0.1067
pt(t2,df=56,lower.tail=T)
常数项操作步骤一样,得到结果小于0.05就可以认为显著非零。
上面的东西小总结
目前来说,给我们一组数据,我们可以先把数据存在一个变量里,然后对数据自动定阶,得到order=c(p,d,q),看看是AR还是MR或者是ARMR,然后可以靠参数估计得到模型的样子,也就是式子的样子,接下来可以判断一下模型是否平稳,我们这一部分刚开始的时候说了arima.sim和filter直观的判别,接着可以用白噪声检测残差,用pt检测参数,看看是不是我们要求的模型。
这里我们顺便说一下AIC准则怎么用,我们在带入数计算后,有时候一组数同时符合两种模型,对于两种模型分别参数估计,找到最后的AIC=的数字,哪个数字小哪个就更好。
预测(forecast)
这是一个很有意思的工具,我们可以靠已有数据来预测之后的数。
在使用之前先调用forecast程序包,然后
forecast(object,h=,level=)
object是拟合信息的文件名,其实搞个变量名也一样。
h是你打算预测多少期
level是置信区间的置信水平,不特殊指定,默认为80%和95%的置信区间,举个例子:
x.fore<-forecast(x.fit,h=5)
接下来直接x.fore可以直接得到预测的数
直接plot(x.fore)可以得到图像,由于我们没特殊指定,所以图像上不只有预测的点连成的线,在预测的值上下会出现两个区域,大的是80%置信区间的,小的是95%置信区间的。
在这里我们之前提到的“画图”的东西也能用,可以自己调着玩一玩。
趋势分析
趋势分析,顾名思义就是要研究趋势,把时间作为自变量,要搞的数据作为因变量,建立随时间变化的回归模型。
线性拟合(lm)
直接上式子
lm(Y~,a+X1+X2+...+Xn,data=)
Y是因变量名,也就是y轴上的数据
a是判断是否需要常数项的,a=1,模型有非零常数项,这也是默认设置,a=0,模型不需要常数项
X1,X2,…,Xn是自变量的个数,如果不想一个个打可以直接不输入。
data=是数据框名,可以说是自变量,也就是x轴上的数据,一般是时间。
在搞定lm后,我们可以通过summary(x.fit)来看看拟合的具体信息,然后用x<-ts(x)把x变成时间序列,接着直接plot(x)作出原函数的线作为比较,abline(lm(x~t),col=2)做出拟合后的图像。
最后一点,如果想查看lm得出的结果,用summary(模型式子)
比方说
x<-c(11:15)
t<-c(1:5)
x.fit<-lm(x~t)
summary(x.fit)
x<-ts(x)
plot(x)
abline(lm(x~t),col=2)
不过我的数是随便取的,线重合了,可以随便取几个数看一看。
曲线拟合(nls)
有的数据看上去就不是线性的,那我们可以用曲线拟合。
还是先说拟合模型的本来面目
nls(Y~ f(X1,...,Xn),data=,start=)
y依然是响应变量
X1这些依然是自变量
data依然是数据框名
start是多出的东西,它的效果是如果需要迭代法计算未知参数,可以指定迭代初始值。
这次我们举例用二次型模型举例,即用下面这个模型来拟合,假设只有10个数
![]()
前面往x里输入数据不再赘述,直接上后面的,为了和lm比较,这里两个都写出来
t1<-c(1:10)
t2<-t1^2
x.fit1<-lm(x~t1+t2)
summary(x.fit1)
x.fit2<-nls(x~a+b*t1+c*t1^2,start=list(a=1,b=1,c=1))
summary(x.fit2)
这两种方法的结果是一致的

第一列数字即为各项的系数,前面的字母就是与系数对应的项。
平滑法
平滑法,是通过将已知的数据处理而使序列平滑化的方法。
移动平均法(SMA)
调用SMA首先需要加载TTR程序包并加载,命名的格式是
SMA(x,n=)
格式很短,x是变量名,n是移动平均期数,经过上面的洗礼,这个没啥好说的。
指数平滑法
详细的说,指数平滑法其实常用的有三种方法:简单指数平滑,Holt两参数指数平滑,Holt-Winters三参数指数平滑。但这三个共用一个格式
HoltWinters(x,alpha=,beta=,gamma=,seasonal=)
x还是那个x
alpha=,beta=,gamma=这三个能决定用的是哪个指数平滑法,单个来说
alpha是随机波动部分的参数
beta是趋势部分的参数
gamma是季节部分的参数
这三个确定指数平滑法的方法为:
alpha不指定,beta=F,gamma=F,为简单指数平滑模型
alpha和beta不指定,gamma=F,为Holt两参数指数平滑模型
三个参数都不指定,那就是拟合Holt-Winters三参数指数平滑模型
seasonal是在既含有季节又含有趋势的时候,指定季节和趋势的关系:
seasonal=“additive"表示加法关系,这也是默认项
seasonal="multiplicative"表示乘法关系,举个例子
x.fit<-HoltWinters(x,gamma=F)#Holt两参数指数平滑
x.fit<-HoltWinters(x)#Holt-Winters三参数指数平滑
综合分析(补充一个decompose)
在正式开始之前,我们再认识一个命令:确定性因素分解
decompose(x,type=)
x还是那个x
type是指是加法模型还是乘法模型。
type="additive"是加法模型,也是系统的默认选项
type="multiplicative"是乘法模型,简写为mult
接下来是正式的组合应用,拿例子总结好说明一点,这里还是不再写输入x这一步骤:
plot(x)
x.fit<-decompose(x,type="mult")
x.fit$figure#查看季节指数
plot(x.fit$figure,type="o")
x.fit$trend#查看趋势拟合值
plot(x.fit$trend)
x.fit$random
plot(x.fit$random)
x.fit#这时候我们可以直接看看一看各种数据和图像的汇总
差分运算(diff)
差分运算最基础好用的就是diff函数,格式如下:
diff(x,lag=,differences=)
x还是那个x
lag是差分的步长,默认为1
differences是差分的次数,不指定就视为是1
比如1阶差分就是diff(x),2阶差分就是diff(x,1,2),k阶差分就是diff(x,1,k),d步差分就是diff(x,d,1)直接写成diff(x,d)也行,玩点花的,先一阶差分后再进行d步差分diff(diff(x),d)
疏系数模型(加料版arima)
疏系数一般用arima函数拟合,命令为:
arima(x,order=,include.mean=,method=,transform.pars=,fixed=)
是不是有点眼熟?我们在参数估计里提到过,但这次的模型更长了。
x还是那个x
order与上面提到的order是一样的,基础型为order=c(p,d,q),p为自回归阶数,d为差分阶数,q为移动平均阶数
include.mean用于判断是否需要拟合常数项
include.mean=T,需要拟合常数项,include.mean=F,不需要拟合常数项
method用于指定参数估计的方法,在上面也有提到,
method="CSS-ML"是条件最小二乘估计和极大似然估计混合方法,method="ML"是极大似然估计,method="CSS"是条件最小二乘估计。
transform.pars是判断指定函数是否由系统自动完成,transform.pars=T,根据order设定自动完成参数估计,transform.pars=F,不能让系统根据模型的最高阶数自动完成所有参数的估计,我们还要人为干预。
fixed是对疏系数模型指定疏系数的位置,其他地方为0,比如fixed=c(NA,0,0,NA)就是1和4两个位置非零,2,3参数恒为0。
举例说明更好说一点,如果要拟合order=c(4,1,0),(这个可以用前面的函数得出来),疏系数模型ARIMA((1,4),1,0)的命令那就是
x.fit<-arima(x,order=c(4,1,0),transform.pars=F,fixed=c(NA,0,0,NA))
结果的看法和arima一致(本来就是一个命令不过加了点东西),记得最后对残差进行白噪声检验。
季节模型(再加料版arima)
季节模型是在疏系数模型的基础上又加了一个seasonal
arima(x,order=,include.mean=,method=,transform.pars=,fixed=,seasonal=)
同样的配方不再赘述,只说唯一多的seasonal
seasonal是指定季节模型的阶数与季节周期,命令格式为:
seasonal=list(order=c(P,D,Q),period=π)
如果是加法模型,则P=0,Q=0;如果是乘法模型,则P,Q不全为零。这里π代指数字。
举个例子,这个例子条件大致和上面那个例子差不多,但变成拟合加法模型ARIMA((1,4),(1,4),0):
x.fit<-arima(x,order=c(4,1,0),seasonal=list(order=c(0,1,0),period=4),transform.par=F,fixed=c(NA,0,0,NA))
加上一个ARIMA(1,1,1)*ARIMA(0,1,1)12模型作为比较:
x.fit<-arima(x,order=c(1,1,1),seasonal=list(order=c(0,1,1),period=12))
这样就好理解多了。当然别忘了对残差序列进行白噪声检验。
DW检验(dwtest)
DW检验全称是Durbin-Watson检验,使用前需要下载并调动调动lmtest程序包。语句起来很简单:
dwtest(x.fit)
x.fit其实就是要用的序列名
得到结果有两个,DW和p值,若DW值小于2且P值极小,那么就可以视为高度正相关。
Durbin h检验(dwtest加料版)
和DW检验不同在多了一个order.by
dwtest(x.fit,order.by=xlag)
后面那个xlag是指自变量。
看的方法和DW检验一样。
ARCH模型(主要是garch)
ARCH模型要用的命令还是比较多的,一共三步,首先需要完成LM检验,然后完成Portmantesu Q检验,最后拟合ARCH模型。
两个检验没啥要说的,看看命令就能明白,解释一下拟合模型:
garch(x,order=)
x还是那个x
order是拟合模型的阶数,拟合ARCH(q)模型那就是order=c(0,q);拟合GARCH(p,q)模型那就是order=c(p,q)
LM检验:
for(i in 1:5) print(ArchTest(x,lag=i))
Portmantesu Q检验:
for(i in 1:5) print(Box.test(x^2,lag=i))
拟合模型:
x,fit<-garch(x,order=c(0,3))
附:绘制条件异方差拟合的95%置信区间
x.pred<-predict(x.fit)
plot(x.pred)
小结
现在我们对于数据的处理可以变成读入数据,画图直观看一看,对差分序列(也就是diff(x))绘图,看自相关图,白噪声检验,接下来自动定阶或者肉眼看看对应的数据,然后参数估计拟合一下ARIMA模型,接下来残差白噪声检验,绘制预测图,Portmantesu Q检验,拟合GARCH模型,最后以绘制波动置信区间收尾。
plot(x)#画x的图像
plot(diff(x))#画差分序列
acf(diff(x))#差分序列的自相关图
pacf(diff(x))#差分序列的偏自系数
for(i in 1:2) print(Box.test(diff(x),lag=6*i))#对差分序列做白噪声检验
x.fit<-arima(x,order=c(,,)
x.fit#看看拟合的模型
for(i in 1:6) print(Box.test(x.fit$residual,type="Ljung-Box",lag=i))#残差白噪声检验
x.fore<-forecast(x.fit,h=365)#水平预测
plot(x.fore)#绘制水平预测图
for( i in 1:6) print(Box.test(x.fit$residual^2,type="Ljung-Box",lag=i))#Portmanteau Q检验
r.fit<-garch(x.fit$residual,order=c(,))#拟合模型
summary(r.fit)#看看模型
r.pred<-predict(r.fit)#和下面这一行合起来是绘制波动置信区间
plot(r.pred)
基础操作的组合结果就是这些。
多元函数(arimax)
首先有一个插曲,ccf(协相关图):
ccf(x,y)
其实这里的x和y的顺序并不太重要,ccf(x,y)是x比y滞后的情况,ccf(y,x)是y比x滞后的情况。
接下来是正餐,arimax:
arimax(y,order=,xreg=,xtransf=,transfer=)
y是要进行拟合的序列名
order是老朋友了,order=c(p,d,q)
xreg是输入的变量名(不需要转移函数变换)
xtransf也是输入的变量名,但这里是需要转移函数变换的
transfer是指定转移函数的模型阶数
针对于这里较为复杂,需要详细分情况举例:
(1)当输入变量是单变量,且不需要做转移函数变换,也就是下面这样的ARIMAX模型:

命令为:
y.fit<-arimax(y,order=c(p,0,q),xreg=x)
(2)当输入变量是多变量,比如两个变量,不需要转移函数变换,也就是和下面这个相符:

y.fit<-arimax(y,order=c(p,0,q),xreg=data.frame(x1,x2))
(3)假设输入变量为单变量,且需要做ARMA(m,n)转移函数变换,这就是这个:

此时命令为:
y.fit<-arimax(y,order=c(p,0,q),xtransf=x,transfer=list(c(m,n)))
(4)假设输入的是多变量,分别需要做ARMA(m1,n1)和ARMA(m2,n2)转移函数变换,也就是这个:
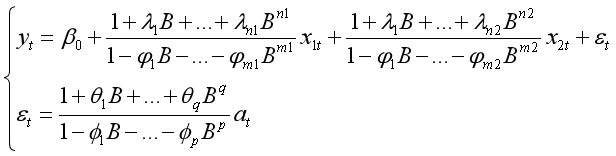
这时,命令为:
y.fit<-arimax(y,order=c(p,0,q),xtransf=data.frame(x1,x2),transfer=list(c(m1,n1),c(m2,n2)))
(5)假设输入变量既有不需要转换函数变换的,又有需要转移函数变换的,也就是这个样子的:
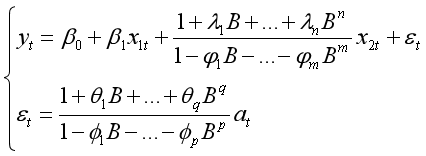
这时候命令为:
y.fit<-arimax(y,order=c(p,0,q),xreg=x1,xtransf=x2,transfer=list(c(m,n)))
单位根检验(sdfTest)
这是最后一部分,单位根检验是检验序列平稳性的统计方法,在使用它之前,我们需要下载并调用fUnitRoots包,它的本体命令如下:
sdfTest(x,lags=,type=)
x,这都到最后了,不用再说它是啥了
lags是延迟阶数,lags=1,这是默认设置,这时候进行DF检验,lags=n,n>1,这时进行ADF检验
type是检验类型,type=“nc”,无常数均值,无趋势类型;type=“c”,有常数均值,无趋势类型;type=“ct”,有常数均值,有趋势类型。
得出结果若高于显著水平,则可以视为非平稳序列。
结束
以上就是R语言进行时间序列分析的基本操作,供我自己回忆以及和广大网友们共勉。
说实话,我不觉得以我自己的描述水准能有人看下来并且看到结尾,如果真的有人看到这里,愿诸君共勉。
参考书:《时间序列分析-基于R》