数据结构堆介绍,图文详解分析——Java/Kotlin双版本代码
堆介绍
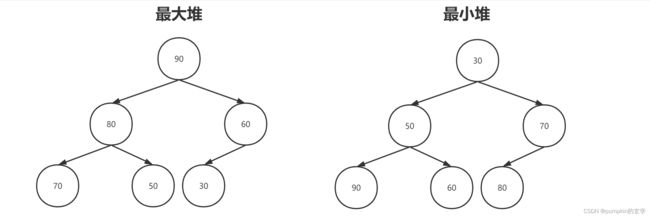
堆是一种特殊的树结构。根据根节点的值与子节点值的大小关系,堆又分为最大堆和最小堆。
最大堆:每个节点的值总是大于或者等于其任意子节点的值。所以最大堆中根节点即为最大值。
最小堆:每个节点的值总是小于或者等于其任意子节点的值。所以最小堆中根节点即为最小值。
堆的特点是最大值或最小值位于堆的顶部,只需要O(1)的时间就可以求出一个数据集合中的最大值或最小值,同时在堆中添加或删除元素的时间复杂度都是O(logn)。因此堆通常用来求一个动态的集合中的k个最大值或者最小值。
堆实现
堆通常使用完全二叉树实现,在完全二叉树中,除了最底层之外其他层均为填满,最底层则是从左到右的顺序排列。所以完全二叉树就可以使用数组进行实现,因此堆也可以使用数组进行实现。
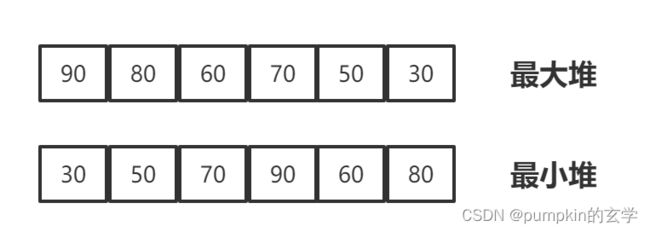
将堆的每一层从左到右的节点按照0,1,2的顺序进行排列。编号0放到数组0的位置,编号1放到数组1的位置,就可以将堆放到数组中去。比如上述最大堆和最小堆,可以使用下方的数据结构进行表示:
用数组表示堆**,如果一个元素在数组中的下表是i,则其在堆中的父节点在数组中的坐标为(i-1)/2,而它的左右子节点在数组中的下标分别为2i+1和2i+2**。
堆的增删
此处使用最大堆进行解释,最小堆和最大堆理论都一样的
最大堆添加节点
- 从上到下,从左右到找到第一个空缺的位置,将新的节点添加到空缺的位置上。
- 对比新节点的值和父节点的值,如果新节点的值比父节点的值大,则交换新节点和父节点的值。
- 重复步骤2,直到新节点的值大于或者等于父节点的值或者已经到达根节点。
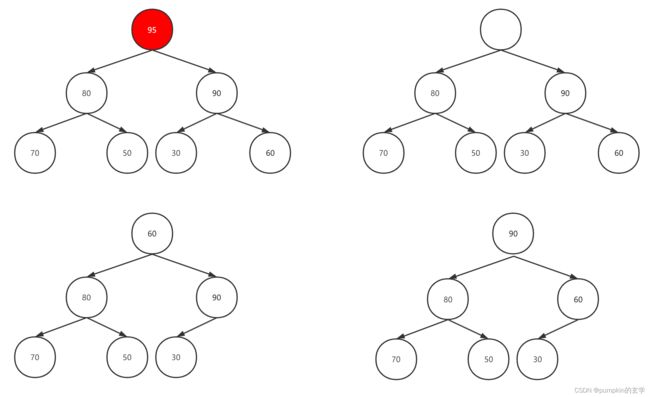
如下,在之前最大堆上添加新元素95,图解过程如下:
最大堆删除节点
通常只删除堆顶部节点,删除步骤如下:
- 删除最大堆顶部节点
- 将堆最底部最右边的节点移到堆的顶部
- 如果存在左右子节点的值大于顶部节点的值,则它和左右子节点值中的最大值进行交换
- 重复上述步骤,直到该节点的值大于或等于其左右子节点的值,或者抵达最后一层。
如下,删除最大堆元素95,图解过程如下:
时间复杂度
基于上述的描述,从堆里面获取最大值或者最小值的时间复杂度为O(1)。
对堆进行增减或者删除的时间复杂度为树高O(logn)。
堆的应用
java使用PriorityQueue实现了堆数据结构。PriorityQueue默认的情况下是一个最小堆,如果要使用最大堆则需要自己传入Comparator。
PriorityQueue实现了Queue接口,其常用的函数如下所示:
| 操作 | 抛异常 | 不抛异常 |
|---|---|---|
| 插入新的元素 | add(e) | offer(e) |
| 删除堆顶元素 | remove | poll |
| 返回堆顶元素 | element | peek |
通常使用堆求取一个动态数据集合中最大或者最小的k个元素。通常,使用最小堆求取集合中k个最大的元素,使用最大堆求取集合中k个最小的元素。
题目:设计一个数据结构,它每次从一个数据流中读取一个数字,并得出数据流已经读出的数字中第k(k>1)大的数字。该数据结构有一个构造器,构造器接受一个参数k(整数),另外接收一个数组(假设数组长度大于k)。还有一个函数add用来动态的添加数字,并返回此时读取中的第k大的值。
列如:当k=2,nums数组为[4,3,5,6],调用构造函数初始化之后,第一次调用add传入7此时应返回6,再次调用add传入8此时应该返回7。
分析:数据流相关的特点是输入的数据是动态添加且无限的。所以我们需要一个数据结构每次只保存之前k大的几个值,每次add的时候,只需要判断保存的值里面的最小值是否小于add的值,如果小于则替换即可。所以这里可以使用最小堆。
代码参考:
kotlin 版本
class HeapTest(val k: Int, num: Array<Int>) {
private val minHeap = PriorityQueue<Int>()
init {
for (i in num) {
add(i)
}
}
fun add(e: Int): Int {
if (minHeap.size < k) {
minHeap.offer(e)
} else if (minHeap.peek() < e) {
minHeap.poll()
minHeap.offer(e)
}
return minHeap.peek()
}
}
测试
val heapTest = HeapTest(3, arrayOf(4, 5, 8, 2))
println(heapTest.add(3))
println(heapTest.add(5))
//结果
第一次调用 传入3 返回4
第二次调用 传入5 返回5
java 版本
public class HeapTestJava {
private final PriorityQueue<Integer> minHeap = new PriorityQueue<>();
private final int k;
public HeapTestJava(int k, int[] num) {
this.k = k;
for (int i : num) {
add(i);
}
}
public int add(int v) {
if (minHeap.size() < k) {
minHeap.offer(v);
} else if (v > minHeap.peek()) {
minHeap.poll();
minHeap.offer(v);
}
return minHeap.peek();
}
}
♀️。欢迎技术探讨噢!