[ICLR19] IMPROVING MMD-GAN TRAINING WITH REPULSIVE LOSS FUNCTION
本篇是ICLR2019的oral paper。[github]
ABSTRACT
生成对抗性网络(GANs)被广泛用于学习数据采样过程,在有限的计算预算下,其性能可能在很大程度上取决于损失函数。本研究修正了用maximum mean discrepancy最大平均偏差(MMD)作为GAN损失函数的MMD-GAN,并提出了两个贡献。
- 首先,我们认为现有的MMD损失函数可能会阻碍学习数据中的细节,因为它试图缩小真实数据的识别器输出。为了解决这个问题,我们提出了一个排斥损失函数(repulsive loss function),通过简单地重新排列MMD中的公式来主动学习实际数据之间的差异。
- 其次,受hinge loss的启发,我们提出了一个有界高斯核来稳定具有排斥损耗函数的MMD-GAN的训练。该方法适用于CIFAR-10、STL-10、CelebA和LSUN卧室数据集上的无监督图像生成任务。
结果表明,在不增加计算成本的情况下,排斥损失函数较MMD损失函数有明显的改善,并优于其他具有代表性的损失函数。所提出的方法使用一个DCGAN网络和谱归一化(Spectral Normalization),在CIFAR-10数据集上获得了16.21的FID分数。
1 INTRODUCTION
生成对抗网络(GANs) (Goodfellow et al.(2014))是生成模型的一个分支,它学习模仿真实的数据生成过程。近年来,GANs得到了深入的研究,并获得了各种成功的应用(Karras et al. (2018); Li et al. (2017b); Lai et al. (2017); Zhu et al. (2017); Ho & Ermon (2016))。GANs的思想是联合训练一个试图生成人工样本的生成器网络和一个区分生成的样本和真实样本的判别器网络。与基于极大似然的方法相比,GANs更倾向于生成具有更清晰、更生动细节的样本,但需要更多的训练。
近年来关于改进GAN培训的研究主要集中在损失函数、网络结构和训练流程的设计上。损失函数,或简单的损失,定量地定义了鉴别器输出的差异之间的实际和生成的样本。利用损失函数梯度训练发生器和鉴频器。本研究关注的损失函数称为最大平均偏差(MMD),即两个概率分布之间的距离度量,广泛应用于核二样本检验(Gretton et al., 2012)。理论上,当且仅当两种分布相等时,MMD达到全局最小值为零。因此,MMD被用来直接将生成的样本与真实样本进行比较(Li et al. (2015);(Dziugaite et al.(2015)),并将其作为损失函数扩展到GAN框架(Unterthiner et al. (2018); Li et al. (2017a); Binkowski et al. (2018))。
在这篇文章中,我们解释了MMD损失的优化由判别器作为吸引和排斥过程的组合,类似于线性判别分析。我们认为,现有的MMD损失可能阻碍学习数据中的细节,因为判别器试图将其输出的组内方差最小化。为了解决这个问题,我们提出了一个斥性损失的判别器,显式地探索了实际数据之间的差异。该方法在图像生成方面比MMD方法有明显的改进了四个基准数据集的任务,而不产生任何额外的计算成本。在此基础上,提出了一种有界高斯核函数来稳定鉴别器的训练。因此,与Li等人(2017a)和Binkowski等人(2018)使用的线性组合内核相比,在MMD-GAN中使用单个内核就足够了。通过使用单个内核,可以在各种应用程序中潜在地降低MMD损失的计算成本。
论文组织如下。第2节回顾了使用MMD损失(MMDGAN)训练的GANs。我们在第3节中提出了判别器的排斥损耗,在第4节中介绍了稳定训练过程的两种实用技术,并在第5节中给出了大量实验结果。在最后一节中,我们将讨论模型和现有工作之间的联系。
2 MMD-GAN
在本节中,我们将介绍GAN模型和MMD损耗。考虑一个随机变量![]() ,它的经验数据分布为
,它的经验数据分布为![]() 。一个典型的GAN模型包含两个神经网络:生成器G和判别器D。生成器G映射一个隐层编码
。一个典型的GAN模型包含两个神经网络:生成器G和判别器D。生成器G映射一个隐层编码![]() 固定分布
固定分布![]() (如高斯)数据空间
(如高斯)数据空间![]() ,
,![]() 代表生成的样本分布
代表生成的样本分布![]() 。判别器评估分数
。判别器评估分数![]() 真正的或生成样本。这项研究侧重于图像生成任务使用卷积神经网络(CNN)的G和D。
真正的或生成样本。这项研究侧重于图像生成任务使用卷积神经网络(CNN)的G和D。
提出了几个损失函数来量化真实样本和生成样本之间的分数差:![]() ,包括极小值损失和非饱和损失(Goodfellow et al.(2014))、hinge损失(Tran et al.(2017))、Wasserstein损失(Arjovsky et al. (2017);Gulrajani等(2017)和maximum mean difference (MMD) (Li等(2017a);(见附录B.1)。其中,MMD使用核嵌入
,包括极小值损失和非饱和损失(Goodfellow et al.(2014))、hinge损失(Tran et al.(2017))、Wasserstein损失(Arjovsky et al. (2017);Gulrajani等(2017)和maximum mean difference (MMD) (Li等(2017a);(见附录B.1)。其中,MMD使用核嵌入![]() 与特征相关内核k,
与特征相关内核k,![]() 是无限维度
是无限维度![]() 。均方MMD在两个分布P和Q间的距离:
。均方MMD在两个分布P和Q间的距离:(1)。内核
![]() 评估a和b两个样本之间的相似性措施。Gretton et al. (2012)证明,使用一个特征内核
评估a和b两个样本之间的相似性措施。Gretton et al. (2012)证明,使用一个特征内核![]() ,当且仅当
,当且仅当![]() 时才相等地应用。
时才相等地应用。
在MMD-GAN中,判别器D可以解释为形成一个新内核与![]() 。如果D是单射的,
。如果D是单射的,![]() 是特点内核,
是特点内核,![]() 达到最小当且仅当
达到最小当且仅当![]() (Li et al. (2017a))。因此,G和D的目标函数可以为(Li et al. (2017a); Binkowski et al. (2018)):
(Li et al. (2017a))。因此,G和D的目标函数可以为(Li et al. (2017a); Binkowski et al. (2018)):
MMD- GAN已被证明比直接使用MMD作为生成器G的损耗函数的模型更有效(Li et al. (2017a))。
Liu等(2017)研究表明,相对于Jensen Shannon (JS)散度(与极小值损失相关)和总变差(TV)距离(与铰链损失相关),MMD和Wasserstein度量对GAN的目标函数较弱。其原因是,在js散度和电视距离下PG到PX的收敛性也意味着在MMD和Wasserstein度量下的收敛性。弱度量是可取的,因为它们提供了更多关于调整模型以适应数据分布的信息(Liu et al.(2017))。Nagarajan & Kolter (2017)证明了利用模型参数的极小极大损失梯度更新训练的GAN局部指数稳定,接近平衡,而利用Wasserstein损失训练的GAN则不稳定。在附录A中,我们证明了梯度下降训练的MMD-GAN在平衡附近是局部指数稳定的。
3 REPULSIVE LOSS FUNCTION
在本节中,我们将MMD-GAN(使用![]() )的训练解释为引力和斥力过程的结合,并通过重新排列
)的训练解释为引力和斥力过程的结合,并通过重新排列![]() 中的分量,为判别器提出了一个新的repulsive损失函数。
中的分量,为判别器提出了一个新的repulsive损失函数。
首先,考虑线性判别分析(LDA)模型作为判别器。的任务是找到一个投影w群体间的方差最大化![]() 和方差最小化
和方差最小化![]() ,
,![]() 是组均值和协方差。
是组均值和协方差。
在MMD-GAN中,神经网络判别器的工作原理与LDA相似。通过最小化![]() ,判别器D处理两个任务:1)D降低
,判别器D处理两个任务:1)D降低![]() ,即,使两组
,即,使两组![]() 相互排斥(见图1a橙色箭头),或使组间方差最大;2) D增加
相互排斥(见图1a橙色箭头),或使组间方差最大;2) D增加![]() ,即每组内收缩
,即每组内收缩![]() (见图1a蓝色箭头),或使组内方差最小化。我们将收缩真实数据得分的损失函数称为有吸引力的损失。
(见图1a蓝色箭头),或使组内方差最小化。我们将收缩真实数据得分的损失函数称为有吸引力的损失。
我们认为,有吸引力的损失![]() (Eq. 3)有两个问题,可能放缓GAN的训练
(Eq. 3)有两个问题,可能放缓GAN的训练
- 判别器D可能更关注真实样本之间的相似性(以便缩小{D(x)}),而不是区分它们的细节。最初,G生产低质量的样品,D学习{x}的共同特征,以便区分{x}和{y}可能是足够的。只有当{D(y)}足够接近{D(x)}时,D才会了解{x}的细节,以便能够将{D(x)}与{D(y)}分开。因此,D可能会在真实的样本中遗漏一些细节,因此G在训练过程中无法接触到这些细节。
- 如图1a所示,在
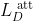 (即
(即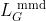 )中,引力(蓝色箭头)和斥力(橙色箭头)项对D(y)的梯度在训练过程中可能有相反的方向。即使D(y)离D(x)很远,它们的和也可能很小,这可能导致G局部停滞。
)中,引力(蓝色箭头)和斥力(橙色箭头)项对D(y)的梯度在训练过程中可能有相反的方向。即使D(y)离D(x)很远,它们的和也可能很小,这可能导致G局部停滞。
因此,我们提出D的排斥损失,以鼓励对真实数据的排斥值{D(x)}:
![]()
生成器G使用与以前相同的MMD损失![]() (见式2),因此,对手在于D通过使
(见式2),因此,对手在于D通过使![]() 最大化而收缩{D(y)}(见图1b),而G膨胀{D(y)}(见图1c)。此外,D也学会独立的真正的数据通过最小化
最大化而收缩{D(y)}(见图1b),而G膨胀{D(y)}(见图1c)。此外,D也学会独立的真正的数据通过最小化![]() 积极探讨了实际样品细节,可能会导致更多的有意义的梯度g .注意情商。4 D没有明确的平均分数离的{D (y)} {D (x)},因为它可能没有影响成对样本距离。但G的目标是匹配两组的平均得分。因此,我们认为,与使用
积极探讨了实际样品细节,可能会导致更多的有意义的梯度g .注意情商。4 D没有明确的平均分数离的{D (y)} {D (x)},因为它可能没有影响成对样本距离。但G的目标是匹配两组的平均得分。因此,我们认为,与使用![]() 和
和![]() 的模型相比,当{D(y)}和{D(x)}不同时,我们的
的模型相比,当{D(y)}和{D(x)}不同时,我们的![]() 和
和![]() 模型不太可能产生相反的梯度(见图1c)。在附录A中,我们证明了梯度下降训练的GAN和排斥MMD损失(L代表D, Lmmd G)是局部指数稳定的接近平衡。
模型不太可能产生相反的梯度(见图1c)。在附录A中,我们证明了梯度下降训练的GAN和排斥MMD损失(L代表D, Lmmd G)是局部指数稳定的接近平衡。
最后,我们确定了判别器D的一般损失函数形式:
λ是超参数。当λ< 0时,判别器损失![]() ,与λ= 1对应于原始的MMD损失
,与λ= 1对应于原始的MMD损失![]() ;当λ> 0,
;当λ> 0,![]() 是repulsive和λ= 1对应于
是repulsive和λ= 1对应于![]() 。有趣的是,当λ> 1时,判别器明确
。有趣的是,当λ> 1时,判别器明确![]() 通过最大化
通过最大化![]() ,这可能是一个惩罚,阻止了成对{D (x)}的距离增加过快。注意,
,这可能是一个惩罚,阻止了成对{D (x)}的距离增加过快。注意,![]() 有相同的计算成本一样
有相同的计算成本一样![]() ,我们只有重置
,我们只有重置![]() 。
。
4 REGULARIZATION ON MMD AND DISCRIMINATOR
在本节中,我们提出了两种方法来稳定MMD-GAN的训练:1)一个有界核,以避免由于过于自信的判别器引起的饱和问题;2)采用广义幂迭代法估计卷积核的谱范数,在本研究的所有实验中,除另有规定外,均采用广义幂迭代法对判别器进行谱归一化。
4.1 KERNEL IN MMD
对于MMD-GAN,使用了以下两个内核:
- 高斯径向基函数(RBF),或高斯内核(Li et . (2017)),
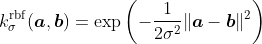 ,σ> 0是内核规模或带宽。
,σ> 0是内核规模或带宽。 - Rational quadratic kernel(Binkowski et al . (2018)),
 ,在内核规模α> 0对应的混合高斯内核与γ(α,1)之前在逆内核尺度
,在内核规模α> 0对应的混合高斯内核与γ(α,1)之前在逆内核尺度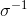 。
。
有趣的是,这两项研究都使用了五种不同核尺度的内核的线性组合,即(见图2和2 c插图)。我们怀疑原因是当ka bk与核尺度相比过大或过小时,单个核k(a, b)饱和(见图2b和2d),这可能导致训练过程中的梯度减小。Li等(2017a)和Binkowski等(2018)都对鉴别器参数进行了惩罚,但对MMD损失本身没有进行惩罚。因此,饱和问题可能仍然存在。使用具有不同内核规模的内核的线性组合可以缓解这个问题,但不能根除它。
受hinge损耗的启发(见附录B.1),我们提出了一个有界RBF (RBF- b)核用于鉴别器。这个想法是为了防止D将{D(x)}推得离{D(y)}太远而导致饱和。对于式3中的L att D, RBF-B核为
对![]() 式4中,RBF-B核为:
式4中,RBF-B核为:
其中bl和bu是下界和上界。因此,单一的内核是充分的和我们设置![]() 实验为简单起见为未来的工作和离开他们的调优。需要注意的是,与铰链损耗的情况一样,RBF-B核仅用于鉴别器,以防止它过于自信。该发生器始终使用原始RBF核进行训练,因此我们保留了MMD损失L MMD G的解释作为度量。
实验为简单起见为未来的工作和离开他们的调优。需要注意的是,与铰链损耗的情况一样,RBF-B核仅用于鉴别器,以防止它过于自信。该发生器始终使用原始RBF核进行训练,因此我们保留了MMD损失L MMD G的解释作为度量。
RBF-B核是解决饱和问题和稳定MMD-GAN训练的众多方法之一。我们发现随机抽样内核规模、实例噪声(Sønderby et al .(2017))和标签平滑(Szegedy et al。(2016);Salimans等(2016))也可能改善模型性能和稳定性。然而,RBF-B核的计算成本相对较低。
4.2 SPECTRAL NORMALIZATION IN DISCRIMINATOR
在没有任何Lipschitz约束的情况下,判别器D可以简单地增加输出的大小,使判别器损失最小化,从而导致训练不稳定3。谱归一化将每一层的权矩阵除以其谱范数,对D的每一层的输出量和梯度大小施加一个上界(Miyato et al.(2018))。然而,为了估计卷积核的频谱范数,Miyato等人(2018)将核重构为矩阵。我们提出了一种直接估计卷积核光谱范数的广义幂迭代方法(详见附录C),并在所有实验中将光谱归一化应用于判别器。在附录D.1中,我们探讨了使用梯度惩罚来施加Lipschitz约束(Gulrajani et al. (2017);Binkowski等(2018);Arbel等人(2018))提出的排斥损失。
5 EXPERIMENTS
6 DISCUSSION
本研究扩展了前人在MMD-GAN (Li et al. (2017a))方面的工作,有两个贡献。首先,我们将MMD损失的优化解释为吸引和排斥过程的结合,并提出了一个针对主动学习真实数据之间差异的鉴别器的排斥损失。其次,我们提出了一个有界高斯RBF (RBF- b)核来解决饱和问题。经验上,我们观察到由于初始化(附录A.2)、学习率(图3b)和对鉴别器的Lipschitz约束(附录C.3)等因素,排斥损失可能导致训练不稳定。在许多情况下,RBF-B内核成功地稳定了MMD-GAN训练。在RBF-B内核中调整超参数或使用其他正则化方法可以进一步改善我们的结果。
MMD-GAN的理论优势要求鉴别器是单射的。提出的排斥力损失(式4)试图通过显式地最大化实际样品之间的成对距离来实现这一点。Li等人(2017a)采用鉴频器作为编码器,辅助网络作为解码器重构真实生成的样本,实现了注入特性,其计算范围比我们提出的方法更为广泛。另一方面,Binkowski等(2018);Arbel等(2018)通过梯度惩罚对MMD-GAN中的鉴别器施加了Lipschitz约束,这可能并不一定促进单射鉴别器。
排斥真实样本分数的观点与现有研究一致。集成标签可以显著提高生成样本的质量,这已被广泛接受(Odena et al. (2017);Miyato,小山(2018);Zhou等(2018))甚至是k-means方法生成的伪标签(Grinblat等(2017))。原因可能是标签有助于集中来自同一个类的数据,并将它们从不同的类中分离出来。使用预训练的分类器也可以帮助生成生动的图像样本(Huang et al.(2017)),因为学习到的真实样本在分类器隐藏层中的表示方式往往能够很好地分离/组织,并可能对生成器产生更有意义的梯度。