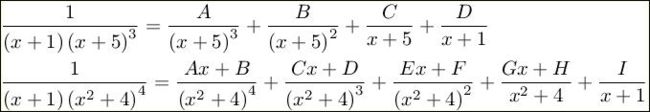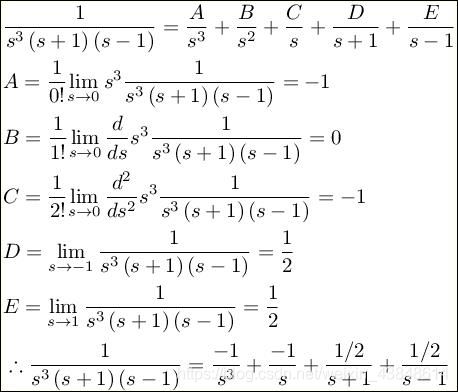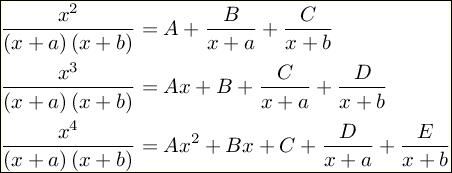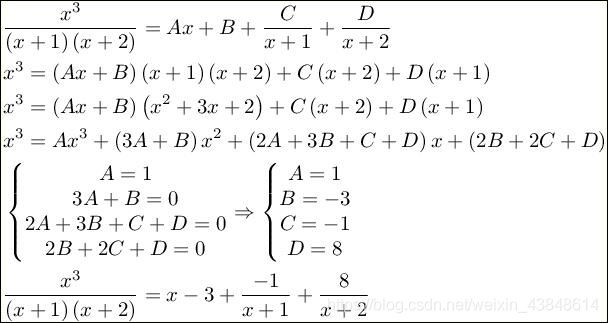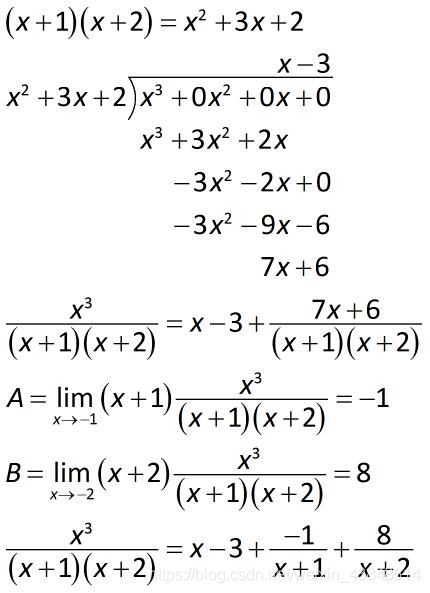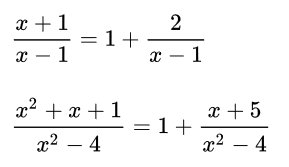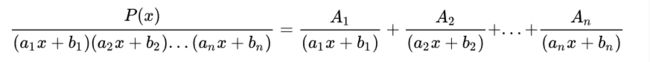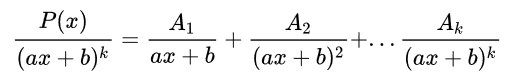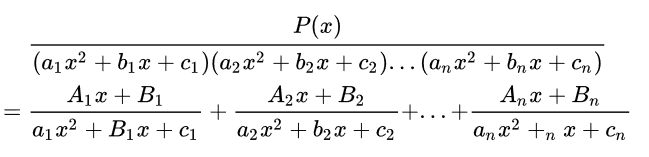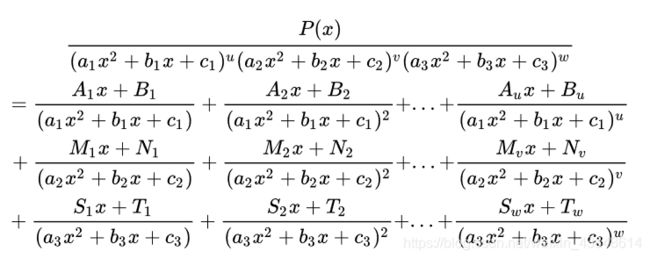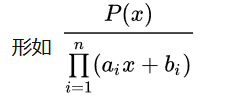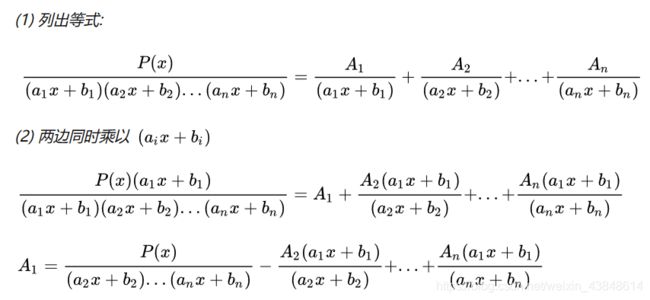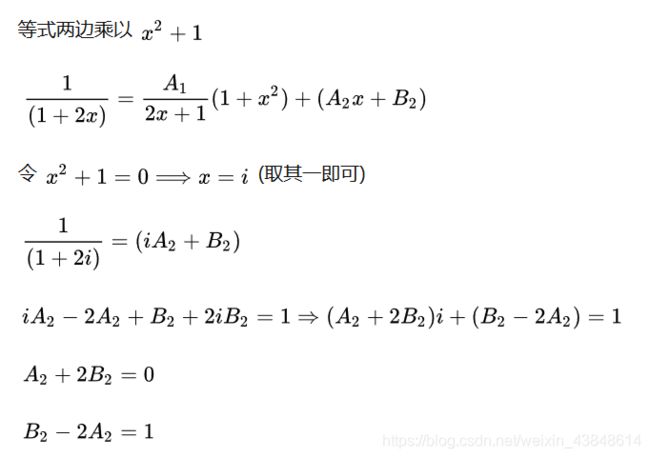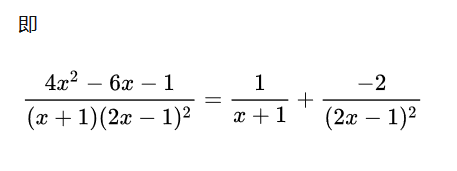【数学】有理分式的拆解技巧

仅做个人学习总结使用
参考的文章：
https://www.jianshu.com/p/1f6025995502
https://zhuanlan.zhihu.com/p/69471608

相信大家都不会陌生，经常遇见含有这些分式的积分类型
现在说说有哪些技巧可以简单应付

一个真分式，分子的次数 < 分母的次数
我们把一个真分式拆解为几个小分式，通常第一步会先把分母进行因式分解，然后按照那个因式分裂为小分式

对于小分式，分子的次数 总会 比分母的次数少1次方：deg(分子) = deg(分母) - 1
例如分母是二阶 $a{x}^2+bx+c$，则分子为$Ax+B$
若分母是一阶 $ax+b$，则分子为常数A

不过，对于高阶极点来说，小分式的个数 = 分母的因式个数
例如$(x+5{)}^3$，因式为$(x+5{)}^3$，$(x+5{)}^2$，$(x+5)$，共三个因式
$(x^2+4 )4，因式为(x2+4)4，(x2+4)3，(x2+4)2，(x^2+4)，共四个因式

常用的方法无非都是那几种：
添项减项法：这个方法对

$\frac{1}{(x+a)(x+b)}$

$1/[(x+a)(x+b)]$

型有效
待定系数法：即小分式通分后，把分子与原式的分子恒等，从而解出对应系数
留数法：即通过消去零因式来解出系数，分母要求为线性(ax+b)型因式，可以是高阶极点
这个方法其实跟z变换类似

添项减项法 和 待定系数法：

留数法：

留数法对于一次因式，一阶极点的因式时最好用的
例如：

而待定系数法，则需要对联立多元方程有很好的运算技巧
通常对于二次或以上的因式最好用
例如：

下面是练习，你们可以试试：

如果分子的次数 ≥ 分母的次数，这是假分式，设法自然会有些改变

这个可依旧运用待定系数法：

或者多项式除法：

图5留数法第二道题解答有点错误，应该对A那个式子求导。希望作者更正下。☺☺☺

https://zhuanlan.zhihu.com/p/69471608

分解步骤总览：

1. 判别真假分式.

2. 真分式分解出待定式.

3. 待定系数求解方法: 实根法(一次式), 复根法(二次式), 求导法(一次n重), 极限法(一、二次的二重)

4. 判别真假分式

形如 $\frac{P(x)}{Q(x)}$
的分式, 若分子指数等于或高于分母, 则要化为真分式.[1]

化简方法: 做多项式除法[2]

例如:

2. 真分式分解

[公式] 重一次因式

形如: $\frac{P(x)}{(Ax+b{)}^k}$

当 $k=1$时

其中$A_i$为待定系数.

当 $k>1$ 时

例如:

$A_i,B_i,C_i$ 为待定系数.

$k$ 二次因式

形如

$\frac{P(x)}{(a{x}^2+bx+c{)}^k}$

当$k=1$时,

当$k>1$时,

例如:

3. 待定系数求解[3]

   无特征——反解方程法

将各项通分合并, 将分子与原式的分子做系数比对, 写出关于待定系数的方程, 进行求解

多个不同的一次式, 且无重因式——实根代入法