光流法简介
光流是指在连续的两帧图像中由于图像中的物体移动或者摄像头的移动导致的目标中目标像素的移动,光流是二维矢量场,表示了一个点从第一帧到第二帧的位移。
光流法的工作原理基于如下假设:
- 相邻帧之间的亮度恒定;
- 相邻视频帧的取帧时间连续,或者,相邻帧之间物体的运动比较“微小”;
- 同一子图像的像素点具有相同或相似的运动。
传统算法——Lucas-Kanade算法:
第一帧中的像素 I ( x , y , t ) I(x, y, t) I(x,y,t)表示在时刻t时像素 I ( x , y ) I(x, y) I(x,y)的值,在经过 Δ t \Delta t Δt时间后,该像素在下一帧中移动了 ( Δ x , Δ y ) (\Delta x, \Delta y) (Δx,Δy),在假设中,这些像素在理想情况下应当是相等的,即:
I ( x , y , t ) = I ( x + Δ x , y + Δ y , t + Δ t ) I(x, y, t)=I(x + \Delta x, y + \Delta y, t + \Delta t) I(x,y,t)=I(x+Δx,y+Δy,t+Δt)
假设移动很小,那么右式可以用泰勒公式展开:
I ( x + Δ x , y + Δ y , t + Δ t ) = I ( x , y , t ) + ∂ I ∂ x Δ x + ∂ I ∂ y Δ y + ∂ I ∂ t Δ t + ϵ I(x + \Delta x, y + \Delta y, t + \Delta t) = I(x, y, t) + \frac{\partial I}{\partial x}\Delta x + \frac{\partial I}{\partial y}\Delta y + \frac{\partial I}{\partial t}\Delta t + \epsilon I(x+Δx,y+Δy,t+Δt)=I(x,y,t)+∂x∂IΔx+∂y∂IΔy+∂t∂IΔt+ϵ
其中 ϵ \epsilon ϵ是高阶无穷小,那么就可以得到:
∂ I ∂ x Δ x + ∂ I ∂ y Δ y + ∂ I ∂ t Δ t = 0 ⇒ ∂ I ∂ x Δ x Δ t + ∂ I ∂ y Δ y Δ t + ∂ I ∂ t = 0 \frac{\partial I}{\partial x}\Delta x + \frac{\partial I}{\partial y}\Delta y + \frac{\partial I}{\partial t}\Delta t = 0 \Rightarrow \frac{\partial I}{\partial x}\frac{\Delta x}{\Delta t} + \frac{\partial I}{\partial y}\frac{\Delta y}{\Delta t} + \frac{\partial I}{\partial t} = 0 ∂x∂IΔx+∂y∂IΔy+∂t∂IΔt=0⇒∂x∂IΔtΔx+∂y∂IΔtΔy+∂t∂I=0
将上式简写为:
I x u + I y v + I t = 0 I_{x}u + I_{y}v + I_{t} = 0 Ixu+Iyv+It=0
u u u和 v v v是两个未知数,因此仅有上述一个式子无法求解。回到一开始介绍的假设3,我们可以假设在一个大小为 m × m ( n = m 2 ) m \times m (n=m^{2}) m×m(n=m2)的窗口内,图像的光流是一个恒定值。那么就可以得到以下方程组:
I x 1 u + I y 1 v = − I t 1 I x 2 u + I y 2 v = − I t 2 ⋮ I x n u + I y n v = − I t n I_{x1}u + I_{y1}v = -I_{t1}\\ I_{x2}u + I_{y2}v = -I_{t2}\\ \vdots\\ I_{xn}u + I_{yn}v = -I_{tn} Ix1u+Iy1v=−It1Ix2u+Iy2v=−It2⋮Ixnu+Iynv=−Itn
矩阵化上述式子,可以得到:
[ I x 1 I y 1 I x 2 I y 2 ⋮ ⋮ I x n I y n ] [ u v ] = [ − I t 1 − I t 2 ⋮ − I t n ] ⇒ A V ⃗ = − b \begin{bmatrix} I_{x1} & I_{y1} \\ I_{x2} & I_{y2} \\ \vdots & \vdots \\ I_{xn} & I_{yn} \end{bmatrix} \begin{bmatrix} u \\ v \end{bmatrix}= \begin{bmatrix} -I_{t1} \\ -I_{t2} \\ \vdots \\ -I_{tn} \end{bmatrix}\Rightarrow \mathbf{A} \vec{\mathbf{V}} = -\mathbf{b} ⎣⎢⎢⎢⎡Ix1Ix2⋮IxnIy1Iy2⋮Iyn⎦⎥⎥⎥⎤[uv]=⎣⎢⎢⎢⎡−It1−It2⋮−Itn⎦⎥⎥⎥⎤⇒AV=−b
用最小二乘法解此方程得:
V ⃗ = ( A T A ) − 1 ) A T ( − b ) \vec{\mathbf{V}}=(\mathbf{A}^{T} \mathbf{A})^{-1}) \mathbf{A}^{T}(-\mathbf{b}) V=(ATA)−1)AT(−b)
即
[ u v ] = [ ∑ i = 1 n I x i 2 ∑ i = 1 n I x i I y i ∑ i = 1 n I x i I y i ∑ i = 1 n I y i 2 ] − 1 [ − ∑ i = 1 n I x i I t i − ∑ i = 1 n I y i I t i ] \begin{bmatrix} u \\ v \end{bmatrix}= \begin{bmatrix} \sum\limits_{i=1}^{n}I_{xi}^{2} & \sum\limits_{i=1}^{n}I_{xi}I_{yi}\\ \sum\limits_{i=1}^{n}I_{xi}I_{yi} & \sum\limits_{i=1}^{n}I_{yi}^{2} \end{bmatrix}^{-1} \begin{bmatrix} -\sum\limits_{i=1}^{n}I_{xi}I_{ti}\\ -\sum\limits_{i=1}^{n}I_{yi}I_{ti} \end{bmatrix} [uv]=⎣⎢⎡i=1∑nIxi2i=1∑nIxiIyii=1∑nIxiIyii=1∑nIyi2⎦⎥⎤−1⎣⎢⎡−i=1∑nIxiIti−i=1∑nIyiIti⎦⎥⎤
深度学习算法——FlowNet/FlowNet2.0
输入为待估计光流的两张图像,输出为图像每个像素点的光流。
使用EPE(End-Point-Error)作为损失,该损失定义为预测的光流和groundtruth之间的欧氏距离:
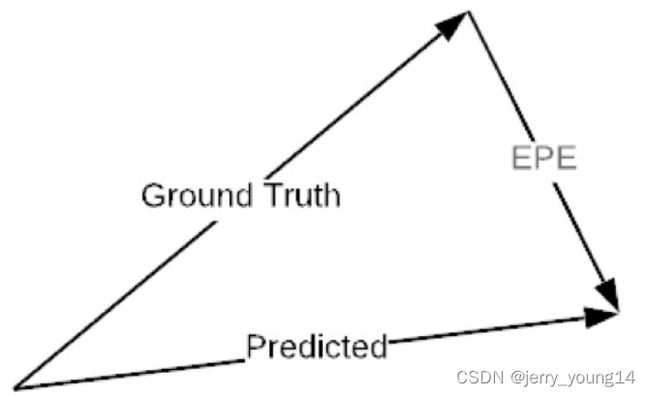
-
FlowNet
对于网络结构,包括Encoder模块和Decoder模块,作者设计两种不同的网络模式:FlowNetSimple和FlowNerCorr。
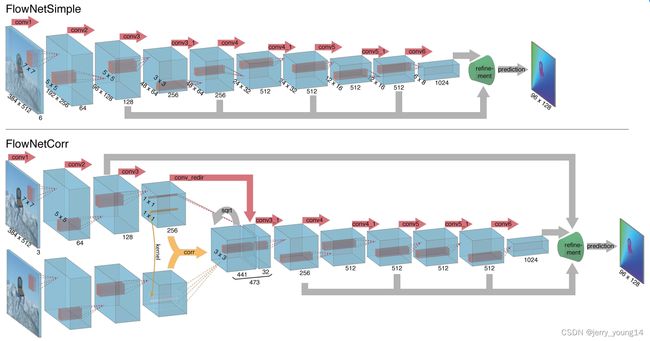
第一种就是简单的两张图象进行通道的拼接,即将两张 h × w × 3 h \times w \times 3 h×w×3的图像合并成 h × w × 6 h \times w \times 6 h×w×6;第二种则是先对两张图像分别进行卷积,获得高层特征后再进行相关性运算,将信息合并。相关性的运算类似于卷积,只不过是两张图像之间的卷积:
c ( x 1 , x 2 ) = ∑ o ∈ [ − k , k ] × [ − k , k ] ⟨ f 1 ( x 1 + o ) , f 2 ( x 2 + o ) ⟩ c(x_{1}, x_{2})=\sum_{o\in [-k, k]\times [-k, k]}\big\langle f_{1}(x_{1}+o), f_{2}(x_{2}+o)\big\rangle c(x1,x2)=o∈[−k,k]×[−k,k]∑⟨f1(x1+o),f2(x2+o)⟩
设置匹配的范围 d d d,那么搜索的范围就为 ( 2 d + 1 ) × ( 2 d + 1 ) (2d+1) \times (2d+1) (2d+1)×(2d+1)的区间,设置像素块尺寸(也即卷积核) 2 k + 1 2k+1 2k+1,那么每一对匹配的像素块需要的计算量为 c ( 2 k + 1 ) 2 c(2k+1)^{2} c(2k+1)2,其中 c c c为通道数,对于每一个像素点,其需要计算的像素块对为 ( 2 d + 1 ) 2 (2d+1)^2 (2d+1)2个,因此总计算量为 w × h × ( 2 d + 1 ) 2 × c ( 2 k + 1 ) 2 w \times h \times (2d+1)^{2} \times c(2k+1)^{2} w×h×(2d+1)2×c(2k+1)2,将每一个像素块对的计算结果按通道数排列,最终得到的特征图尺寸就为 w × h × ( 2 d + 1 ) 2 w \times h \times (2d+1)^{2} w×h×(2d+1)2。图中的 s q r t sqrt sqrt代表开方操作,如果两个图中的像素块一致,那么开方后会得到原有像素块内容, c o n v _ r e d i r conv\_redir conv_redir代表使用 1 × 1 1 \times 1 1×1卷积降维。
refinement为Decoder模块,该模块主体部分是通过反卷积进行升维,其结果如下:
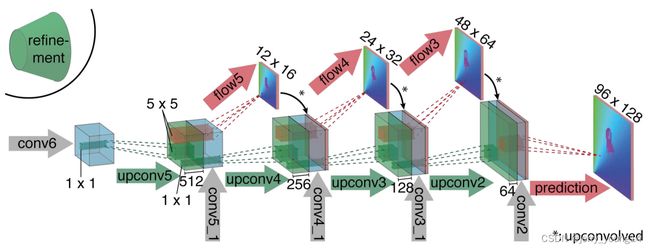
该模块的输入有三个部分,Encoder模块的跳接输入,上一模块的反卷积输出,以及上一模块的光流反卷积输出。红箭头代表卷积,绿箭头代表反卷积,灰箭头代表输入。
-
FlowNet2.0
该网络是对FlowNet的改进,其基于FlowNet中提出的FlowNetSimple(FlowNetS)和FlowNetCorr(FlowNetC)两中网络形式的堆叠组合:
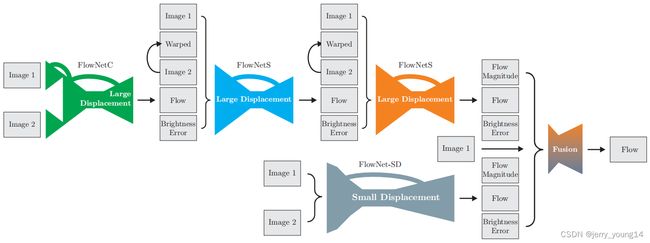
首先,上层模块是FlowNetC和FlowNetS的堆叠组合,首先将两张图片通过FlowNetC,输出一张光流图Flow,将此光流图作用到图2上,即为使用估计的每个像素偏移,偏移图2的每一个像素,使其与图1对齐,该操作得到图即为Warped图。光流估计可能不够准确,因此Warped图与图1存在偏差,将图1的亮度减去Warped图的亮度,即可得到亮度误差图Brightness Error。最后将这5个输出堆叠起来,作为下一个FlowNetS的输入。FlowNet2.0堆叠了两个FlowNetS。原始的FlowNet存在小偏移(Small Displacement)估计不准确的问题,因此在下层模块,作者设计了适合小偏移的FlowNet-SD,其修改了FlowNet中卷积核和 s t r i d e stride stride的大小,使其更适合小偏移。具体的变化为,将FlowNet中 7 × 7 7 \times 7 7×7和 5 × 5 5 \times 5 5×5的卷积核改为 3 × 3 3 \times 3 3×3的卷积核,更小的卷积核意味着更加精细的处理,因此更加适合小偏移估计的问题,并且将 s t r i d e = 2 stride=2 stride=2改为了 s t r i d e = 1 stride=1 stride=1。最后将上下层输出混合,得到最后的光流估计。