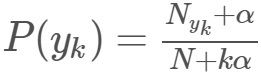MultinomialNB
贝叶斯之多项式朴素贝叶斯
概要:贝叶斯定理是关于随机事件A和B的条件概率(或边缘概率)的一则定理。其中P(A|B)是在B发生的情况下A发生的可能性。多项式朴素贝叶斯多用于高维度向量分类,最常用的场景是文章分类。
语言:python
领域:机器学习
多项式朴素贝叶斯
sklearn.naive_bayes.MultinomialNB(alpha=1.0, fit_prior=True, class_prior=None)
主要用于离散特征分类,例如文本分类单词统计,以出现的次数作为特征值
先验概率 P ( y k ) = N y k + α N + k α P\big(y_k\big)=\frac{N_{yk}+ \alpha }{N+k\alpha} P(yk)=N+kαNyk+α
N是总的样本个数,k是总的类别个数,Nyk是类别为yk的样本个数,α是平滑值
条件概率 P ( x i ∣ y k ) = N y k , x i + α N y k + n α P\big(x_i|y_k\big)=\frac{N_{y_k,x_i}+ \alpha }{N_{y_k}+n\alpha} P(xi∣yk)=Nyk+nαNyk,xi+α
n是特征的维数,Nyk,xi是类别为yk的样本中,第i维特征的值是xi的样本个数,其余参数同上
参数说明:
- alpha:浮点型,可选项,默认1.0,添加拉普拉修/Lidstone平滑参数。当α=1时,称作Laplace平滑,当0<α<1时,称作Lidstone平滑,α=0时不做平滑。
- fit_prior:布尔型,可选项,默认True,表示是否学习先验概率,参数为False表示所有类标记具有相同的先验概率
- class_prior:类似数组,数组大小为(n_classes,),默认None,类的先验概率
| class_prior | fit_prior | class_log_prior_ |
|---|---|---|
| 指定类的先验概率 | True/False | l n ( c l a s s ln(class ln(class_ p r i o r ) prior) prior) |
| None | False | l n 1 k ln\frac{1}{k} lnk1 |
| None | True | l n N y k N ln\frac{N_{yk}}{N} lnNNyk |
| class_prior | fit_prior | 最终先验概率 |
|---|---|---|
| 指定类的先验概率 | True | P ( y k ) = c l a s s P\big(y_k\big)=class P(yk)=class_ p r i o r prior prior |
| 无意义 | False | P ( y k ) = 1 k P\big(y_k\big)=\frac{1}{k} P(yk)=k1 |
| None | True | P ( y k ) = N y k N P\big(y_k\big)=\frac{N_{yk}}{N} P(yk)=NNyk |
N是总的样本个数,k是总的类别个数,Nyk是类别为yk的样本个数,α是平滑值
属性说明:
- class_log_prior_ :各类标记的 平滑 先验概率 对数值,其取值与fit_prior和class_prior参数相关
- intercept_ :其值和class_log_propr相同
- feature_log_prob_ :指定类的各特征概率(条件概率)对数值,返回形状为(n_classes, n_features)数组
- coef_ :其值和feature_log_prob相同
- class_count_ :各类别对应的样本数,按类的顺序排序输出
- feature_count_:各类别各个特征出现的次数,返回形状为(n_classes, n_features)数组:即"类别数"个行,"属性数"个列的矩阵
方法说明:
- predict_proba(X):输出测试样本划分到各个类别的概率值
- score(X, y, sample_weight=None):输出对测试样本的预测准确率的平均值
- set_params(params):设置估计器的参数
- get_params(deep=True):获取分类器的参数,以各参数字典形式返回
- partial_fit(X, y, classes=None, sample_weight=None):对于数据量大时,提供增量式训练,在线学习模型参数,参数X可以是类似数组或稀疏矩阵,在第一次调用函数,必须制定classes参数,随后调用时可以忽略
- predict(X):在测试集X上预测,输出X对应目标值
- predict_log_proba(X):测试样本划分到各个类的概率对数值
- fit(X, y, sample_weight=None):根据X、Y训练模型,即根据【样本X】和【类别Y】拟合线性模型。
参数含义分析:
(1)利用MultinomialNB建立简单模型
import numpy as np
from sklearn.naive_bayes import MultinomialNB
X = np.array([[1,2,3,4],[1,3,4,4],[2,4,5,5],[2,5,6,5],[3,4,5,6],[3,5,6,6]])
y = np.array([1,1,4,2,3,3])
clf = MultinomialNB(alpha=2.0)
clf.fit(X,y)
#clf=MultinomialNB(alpha=2.0, class_prior=None, fit_prior=True)
(2)经过训练后,观察各个属性值
- class_log_prior_:各类标记的平滑先验概率对数值,其取值会受fit_prior和class_prior参数的影响
①指定 class_prior=[0.3,0.1,0.3,0.2] , fit_prior=True/False
则class_log_prior_取值是class_prior转换成log后的结果[log(0.3),log(0.1),log(0.3),log(0.2)]
import numpy as np
from sklearn.naive_bayes import MultinomialNB
X = np.array([[1,2,3,4],[1,3,4,4],[2,4,5,5],[2,5,6,5],[3,4,5,6],[3,5,6,6]])
y = np.array([1,1,4,2,3,3])
#exam1 #fit_prior为True
clf = MultinomialNB(alpha=2.0,fit_prior=True,class_prior=[0.3,0.1,0.3,0.2])
clf.fit(X,y)
print(clf.class_log_prior_)
print(np.log(0.3),np.log(0.1),np.log(0.3),np.log(0.2))
#exam2 #fit_prior为False
clf1 = MultinomialNB(alpha=2.0,fit_prior=False,class_prior=[0.3,0.1,0.3,0.2])
clf1.fit(X,y)
print(clf1.class_log_prior_)
>>output:
[-1.2039728 -2.30258509 -1.2039728 -1.60943791]
-1.20397280433 -2.30258509299 -1.20397280433 -1.60943791243
[-1.2039728 -2.30258509 -1.2039728 -1.60943791]
②class_prior=None , fit_prior=False
则各类标记的先验概率相同等于类标记总个数N分之一: P©=1/4
import numpy as np
from sklearn.naive_bayes import MultinomialNB
x = np.array([[1,2,3,4],[1,3,4,4],[2,4,5,5],
[2,5,6,5],[3,4,5,6],[3,5,6,6]]) #样本属性数据
y = [1,1,4,2,3,3] #样本分类结果
clf = MultinomialNB(alpha=1.0,fit_prior=False,class_prior=None)
clf.fit(x,y)
print(clf.class_log_prior_)#总共4类,所以为log(1/4)
print(np.log(1/4))
>>output:
[-1.38629436 -1.38629436 -1.38629436 -1.38629436]
-1.38629436112
③class_prior=None , fit_prior=True
则各类标记的先验概率,等于各类标记个数除以各类标记个数之和
import numpy as np
from sklearn.naive_bayes import MultinomialNB
X = np.array([[1,2,3,4],[1,3,4,4],[2,4,5,5],[2,5,6,5],[3,4,5,6],[3,5,6,6]])
y = np.array([1,1,4,2,3,3])
clf = MultinomialNB(alpha=2.0,fit_prior=True)
clf.fit(X,y)
print(clf.class_log_prior_)#按类标记1、2、3、4的顺序输出
print(np.log(2/6),np.log(1/6),np.log(2/6),np.log(1/6))
>>output:
[-1.09861229 -1.79175947 -1.09861229 -1.79175947]
-1.09861228867 -1.79175946923 -1.09861228867 -1.79175946923
属性含义分析:
intercept_:将多项式朴素贝叶斯解释的class_log_prior_映射为线性模型,其值和class_log_propr相同
clf.class_log_prior_
>>output:array([-1.09861229, -1.79175947, -1.09861229, -1.79175947])
clf.intercept_
>>output:array([-1.09861229, -1.79175947, -1.09861229, -1.79175947])
feature_log_prob_:指定类的各特征概率(条件概率)对数值,返回形状为(n_classes, n_features)数组
特征的条件概率=(指定类下指定特征出现的次数+alpha)/(指定类下所有特征出现次数之和+类的可能取值个数*alpha)
#(clf见最上面的例子)
clf.feature_log_prob_
##>>output:
array([[-2.01490302, -1.45528723, -1.2039728 , -1.09861229],
[-1.87180218, -1.31218639, -1.178655 , -1.31218639],
[-1.74919985, -1.43074612, -1.26369204, -1.18958407],
[-1.79175947, -1.38629436, -1.23214368, -1.23214368]])
#分类1计算过程
print(
np.log((1+1+2)/(1+2+3+4+1+3+4+4+4*2)),
np.log((2+3+2)/(1+2+3+4+1+3+4+4+4*2)),
np.log((3+4+2)/(1+2+3+4+1+3+4+4+4*2)),
np.log((4+4+2)/(1+2+3+4+1+3+4+4+4*2)) )
##>>output:
-2.01490302054 -1.45528723261 -1.20397280433 -1.09861228867
#解释如下:
#alpha=2.0
#已知x为各个样本对应的向量,值的大小为出现次数
#因此对于分类1(即1)为第1,2两个样本,所以这两个向量相加
#得到 [指定类下指定属性中值出现的次数] [1,2,3,4]+[1,3,4,4]:1+1,2+3,3+4,4+4jfeature_count_:各类别各个特征出现的次数,返回形状为(n_classes, n_features)数组
# [指定类下所有特征出现次数之和] 为1+1+2+3+3+4+4+4
# [类的可能取值个数] 4个属性(1,4,2,3),为4
#特征的条件概率=(指定类下指定特征出现的次数+alpha)/(指定类下所有特征出现次数之和+类的可能取值个数*alpha)=((1+1,2+3,3+4,4+4)+2)/((1+1+2+3+3+4+4+4)+4*2)
x = np.array([[1,2,3,4],
[1,3,4,4],
[2,4,5,5],
[2,5,6,5],
[3,4,5,6],
[3,5,6,6]]) #样本属性数据
y = [1,1,4,2,3,3] #样本分类结果
**coef_:**将多项式朴素贝叶斯解释feature_log_prob_映射成线性模型,其值和feature_log_prob相同
clf.coef_
>>output:
array([[-2.01490302, -1.45528723, -1.2039728 , -1.09861229],
[-1.87180218, -1.31218639, -1.178655 , -1.31218639],
[-1.74919985, -1.43074612, -1.26369204, -1.18958407],
[-1.79175947, -1.38629436, -1.23214368, -1.23214368]])
class_count_:训练样本中各类别对应的样本数,按类的顺序排序输出
clf.class_count_
>>output:
array([ 2., 1., 2., 1.])
feature_count_:各类别各个特征出现的次数,返回形状为(n_classes, n_features)数组
clf.feature_count_
>>output:
array([[ 2., 5., 7., 8.],
[ 2., 5., 6., 5.],
[ 6., 9., 11., 12.],
[ 2., 4., 5., 5.]])
(3)方法
-
fit(X, y, sample_weight=None):根据X、y训练模型
x:样本对应的向量(如向量中各个值的大小为单词出现次数)
y:各样本类别标签
import numpy as np
from sklearn.naive_bayes import MultinomialNB
X = np.array([[1,2,3,4],[1,3,4,4],[2,4,5,5],[2,5,6,5],[3,4,5,6],[3,5,6,6]])
y = np.array([1,1,4,2,3,3])
clf = MultinomialNB(alpha=2.0,fit_prior=True)
clf.fit(X,y)
>>output:MultinomialNB(alpha=2.0, class_prior=None, fit_prior=True)
例子
(1)样本x_ini : 一共6个样本
[['my','my','my','has', 'dog', 'has'],
['not','not', 'take', 'him', 'dog', 'stupid'],
['my', 'cute'],
['stupid', 'garbage'],
[ 'my', 'steak', 'to', 'him'],
['quit', 'dog', 'stupid']]
(2)属性
将单词作为属性,值为单词出现次数
一共有12种单词:从样本中提取,得到12种
['garbage', 'to', 'has', 'him', 'quit', 'my', 'not', 'steak', 'cute', 'take', 'stupid', 'dog']
(3)x: 样本向量
每个样本有12个属性值,值为对应单词在该样本中出现的次数
例如:第一个样本中"my"出现3次,那么在下面第6个值为3
[0, 0, 2, 0, 0, 3, 0, 0, 0, 0, 0, 1]
[0, 0, 0, 1, 0, 0, 2, 0, 0, 1, 1, 1]
[0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0]
[1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0]
[0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0]
[0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1]
(4)y: 类别标签
[0, 1, 0, 1, 0, 1]#第2,4,6个样本属于第1类;第1,3,5个样本属于第二类
numpy.set_printoptions(suppress=True,precision=4)#设置输出精度
print clf.predict_proba(X[0:6]),clf.predict(X[0:6])#predict的结果为概率大的
>>output:
[[0.999 0.001 ]
[0.0071 0.9929]
[0.9168 0.0832]
[0.103 0.897 ]
[0.9529 0.0471]
[0.0683 0.9317]]
[0, 1, 0, 1, 0, 1]
- get_params(deep=True):获取分类器的参数,以各参数字典形式返回
clf.get_params(True)
>>output:{'alpha': 2.0, 'class_prior': None, 'fit_prior': True}
- partial_fit(X, y, classes=None, sample_weight=None):对于数据量大时,提供增量式训练,在线学习模型参数,参数X可以是类似数组或稀疏矩阵,在第一次调用函数,必须制定classes参数,随后调用时可以忽略
import numpy as np
from sklearn.naive_bayes import MultinomialNB
x = np.array([[1,2,3,4],[1,3,4,4],[2,4,5,5],[2,5,6,5],[3,4,5,6],[3,5,6,6]])
y = np.array([1,1,4,2,3,3])
clf = MultinomialNB(alpha=2.0,fit_prior=True)
clf.partial_fit(x,y,classes=[1,2])
clf.partial_fit(x,y)
MultinomialNB(alpha=2.0, class_prior=None, fit_prior=True)
- predict(X):在测试集X上预测,输出X对应目标值
clf.predict([[1,3,5,6],[3,4,5,4]])
>>output:
array([1, 1])
- predict_log_proba(X):测试样本划分到各个类的概率对数值
import numpy as np
from sklearn.naive_bayes import MultinomialNB
x = np.array([[1,2,3,4],[1,3,4,4],[2,4,5,5],[2,5,6,5],[3,4,5,6],[3,5,6,6]])
y = np.array([1,1,4,2,3,3])
clf = MultinomialNB(alpha=2.0,fit_prior=True)
clf.fit(x,y)
MultinomialNB(alpha=2.0, class_prior=None, fit_prior=True)
clf.predict_log_proba([[3,4,5,4],[1,3,5,6]])
>>output:
array([[-1.27396027, -1.69310891, -1.04116963, -1.69668527],
[-0.78041614, -2.05601551, -1.28551649, -1.98548389]])
- predict_proba(X):输出测试样本划分到各个类别的概率值
clf.predict_proba([[3,4,5,4],[1,3,5,6]])
>>output:
array([[ 0.27972165, 0.18394676, 0.35304151, 0.18329008],
[ 0.45821529, 0.12796282, 0.27650773, 0.13731415]])
- score(X, y, sample_weight=None):输出对测试样本的预测准确率的平均值
clf.score([[3,4,5,4],[1,3,5,6]],[1,1])
>>output:
0.5
- set_params(**params):设置估计器的参数
clf.set_params(alpha=1.0)
>>output:
MultinomialNB(alpha=1.0, class_prior=None, fit_prior=True)