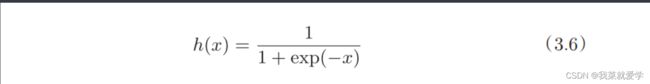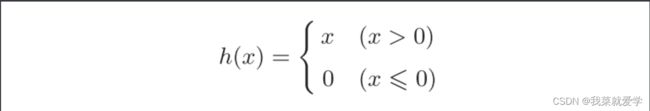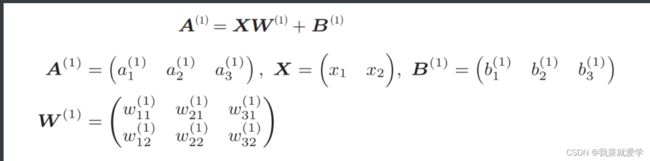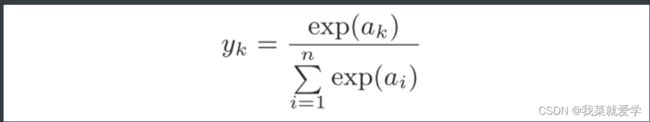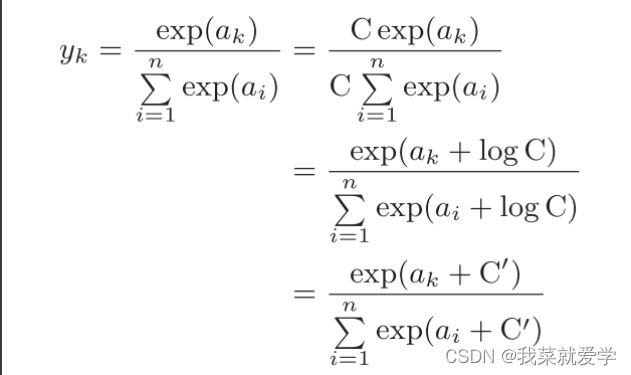【深度学习入门】- 神经网络

欢迎浏览本博客
大家好，我是：我菜就爱学一名刚刚入行的小白
从事方向：计算机视觉
我菜就爱学，分享有误，欢迎大佬指出
本篇介绍：由感知机过度到神经网络，初识神经网络

---

说明：神经网络能够解决感知机的缺陷，可以自动的从数据中学习到合适的权重参数。

1 从感知机到神经网络

1.1 神经网络例子

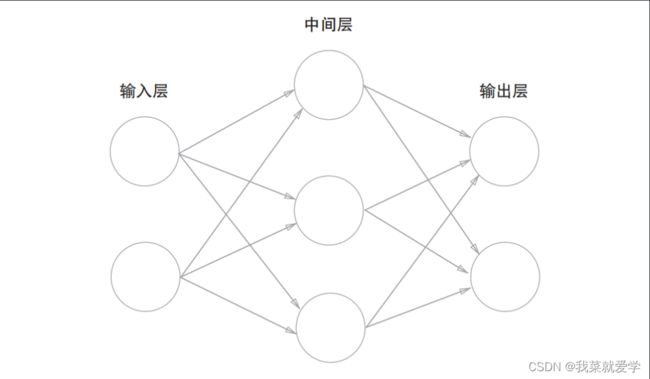
用图表示神经网络的话，把最左边称为输入层，最右边称为输出层。中间的称为中间层，也叫隐藏层。

1.2 激活函数

在感知机中，输入信号的总和会被h(x)转换成输出的信号。h(x)这种函数称为激活函数。
$$y=h(b+w1\ast x1+w2\ast x2)$$
将上面的式子改写之后，先计算输入信号的加权总和
$$a=b+w1\ast x1+w2\ast x2$$
用h()函数将a转换为输出y
$$y=h(a)$$

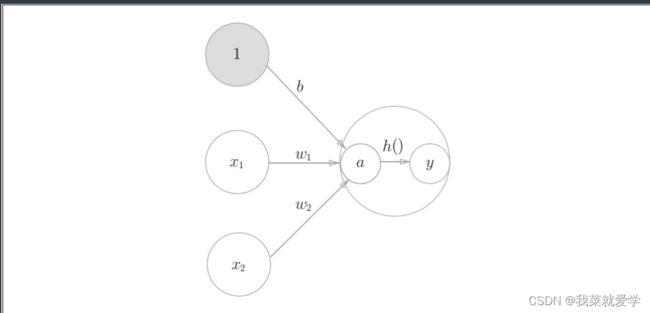
上述图可以看出表示神经元的O显示激活函数的计算过程，即信号的加权总和节点a，然后节点a被激活函数h()转换成节点y。

2 激活函数

说明：在上一节中，感知机的激活函数是以阈值为界，一旦超过阈值，就切换输出。这种激活函数也叫做阶跃函数。若把感知机的阶跃函数换成其他函数，就进入了神经网络。

2.1 sigmoid函数

说明：神经网络中经常使用的一个激活函数就是sigmoid函数。其中exp(-x)表示e(−x)。

2.2 阶跃函数的实现

说明：阶跃函数其实结果就是非0即1.

import numpy as np
x=np.array([-1.0,1.0,2.0])
print(x)
#y作为布尔类型的变量：
#   1、数组x>0的元素被转换为True
#   2、数组<0的元素被转换为False
y=x>0
print(y)
#   再把元素的布尔类型转换为int
y=y.astype(np.int32)
print(y)

画图：

def function(x):
    return np.array(x>0,dtype=np.int32)
x=np.arange(-5.0,5.0,0.1)
y=function(x)
plt.plot(x,y)
plt.ylim(-0.1,1.1)# 指定y轴的范围
plt.show()

2.3 sigmoid函数的实现

1）补充：Numpy广播

若一个2 x 2矩阵A和标量10进行乘法运算，则标量10会自动被扩展成为2 x 2的形状。

A=np.array([[1,2],[3,4]])
B=np.array([10,20])
print(A)
print(A*10)
print(A*B)
'''
[[1 2]
 [3 4]]
 
[[10 20]
 [30 40]]
 
[[10 40]
 [30 80]]
'''

2）sigmoid函数

def sigmoid(x):
    return 1/(1+np.exp(-x))

x=np.arange(-5.0,5.0,0.1)
y=sigmoid(x)
plt.plot(x,y)
plt.ylim(-0.1,1.1)
plt.show()

2.4 阶跃函数和sigmoid函数的比较

def function(x):
    return np.array(x>0,dtype=np.int32)
def sigmoid(x):
    return 1/(1+np.exp(-x))

x=np.arange(-5.0,5.0,0.1)
y1=function(x)
y2=sigmoid(x)
plt.plot(x,y1,linestyle='--',label='jieyue')
plt.plot(x,y2,label='sigmoid')
plt.legend()
plt.ylim(-0.1,1.1)
plt.show()

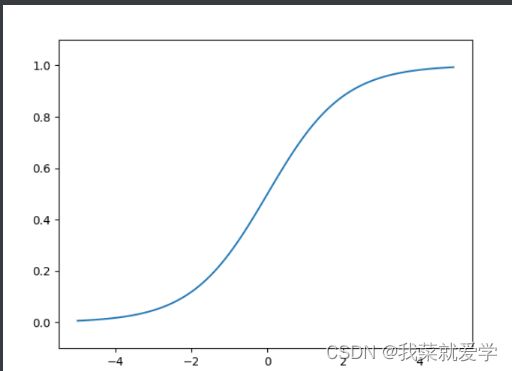
• sigmoid函数是一条平滑的曲线，阶跃函数输出会发生急剧的变化
• 阶跃函数只能返回0和1，而sigmoid返回的是连续的实数

2.5 非线性函数

说明：函数本来是输入某个值之后会返回一个值的转换器，向这个转换器输入某个值后，输出值是输入值常数倍的函数称为线性函数。

神经网络的激活函数必须使用非线性函数。因为线性函数在多层结构中，不管加多少层在隐藏层中都是等效的效果。如h(x)=cx，y(x)=h(h(h(x)))也就是y(x)=c * c * c * x

2.6 ReLU函数

ReLU函数的定义就是在输入函数大于0时，直接输出该值。在输入小于等于0时，输出0。

def reul(x):
    return np.maximum(0,x)

x=np.arange(-5.0,5.0,0.1)
y=reul(x)
plt.plot(x,y)
plt.show()

3 多维数组的运算

3.1 多维数组

1）生成1维数组，查看数组、数组的维度和数组的形状

A=np.array([1,2,3,4])
print(A)
print(A.ndim)
print(A.shape)
print(A.shape[0])
'''
[1 2 3 4]
1
(4,)
4
'''

2）生成一个3 x 2的数组B，表示第一个维度（列）【对应0维】有三个元素，第二个维度（行）【对应1维】有两个元素。同时二维数组也叫做矩阵。

B=np.array([[1,2],[3,4],[5,6]])
print(B)
print(B.ndim)
print(B.shape)
'''
[[1 2]
 [3 4]
 [5 6]]
2
(3, 2)
'''

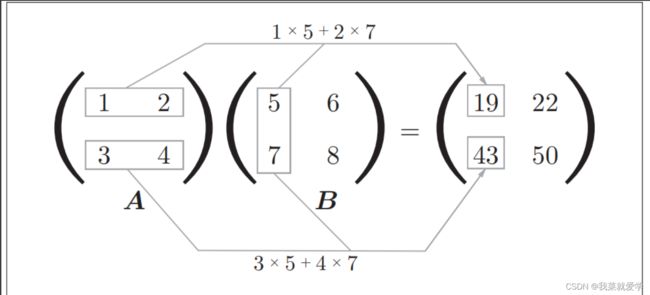
3.2 矩阵乘法

这个线性代数，也有介绍。代码中使用np.dot()作为矩阵的乘法。

A=np.array([[1,2],[3,4]])
B=np.array([[5,6],[7,8]])
print(A)
'''
[[1 2]
 [3 4]]
'''
print(B)
'''
[[5 6]
 [7 8]]
'''
C=np.dot(A,B)
print(C)
'''
[[19 22]
 [43 50]]
'''

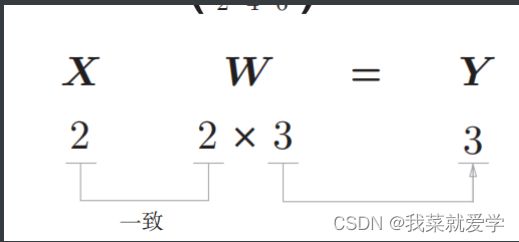
3.3 神经网络的内积

说明：这个时候把X和W分别设置成为可以做矩阵乘法的矩阵。满足如下规则：

X=np.array([1,2])
print(X.shape)  # (2,)->1X2
W=np.array([[1,3,5],[2,4,6]])
print(W.shape)  #(2, 3)->2X3
Y=np.dot(X,W)
print(Y.shape)  #(3,) -> 1X3
print(Y)
# [ 5 11 17]

4 3层神经网络的实现

4.1 符号确认

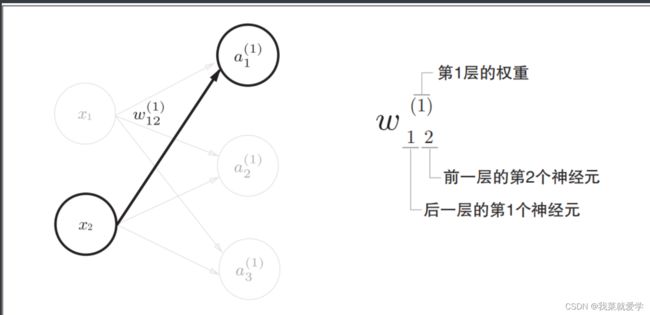
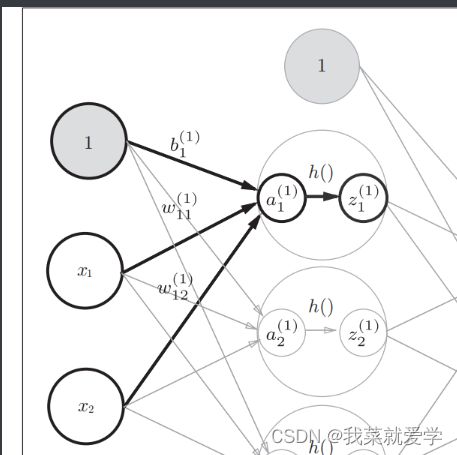
下图显示了从输入层神经元x2到后一层的神经元a1的权重。权重和隐藏层的神经元的右上角有一个“(1)"，它表示权重和神经元的层号（即第1层的权重、第1层的神经元)。权重的右下角还有两个数字，它们是后一层的神经元和前一层的神经元的索引号。如下，表示前一层的第2个神经元x2到后一层的第一个神经元a1的权重。

4.2 各层间信号传递的实现

1）对于如下神经元a1通过加权信号和偏置的方式计算如下：

2）若使用矩阵的乘法运算，则将第一层的加权和表示成下面式子：

3）下面用多维数组代码实现：

X=np.array([1.0,0.5])
W1=np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])
B1=np.array([0.1,0.2,0.3])
print(X.shape)  #   (2,)
print(W1.shape) #   (2, 3)
print(B1.shape) #   (3,)
A1=np.dot(X,W1)+B1
print(A1)
'''
[0.3 0.7 1.1]
'''

4）得到的加权和，再利用加权函数得到Z

def sigmoid(x):
    return 1/(1+np.exp(-x))
 Z1=sigmoid(A1)
print(Z1)
#   [0.57444252 0.66818777 0.75026011]   

5）实现第一层到第二层传递

W2=np.array([[0.1,0.4],[0.2,0.5],[0.3,0.6]])
B2=np.array([0.1,0.2])
print(Z1.shape) #   (3,)
print(W2.shape) #   (3, 2)
print(B2.shape) #   (2,)
A2=np.dot(Z1,W2)+B2
Z2=sigmoid(A2)
print(Z2)   #   [0.62624937 0.7710107 ]

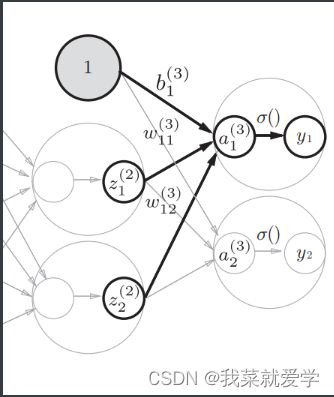
6）第2层到输出层的信号传递。这里最后的激活函数与隐藏层的不同

def function(x):
    return np.array(x>0,dtype=np.int32)
W3=np.array([[0.1,0.3],[0.2,0.4]])
B3=np.array([0.1,0.2])
A3=np.dot(Z2,W3)+B3
print(Z2.shape) #   (2,)
print(W3.shape) #   (2, 2)
print(B3.shape) #   (2,)
Y=function(A3)
print(Y)    #   [1 1]

5 输出层的设计

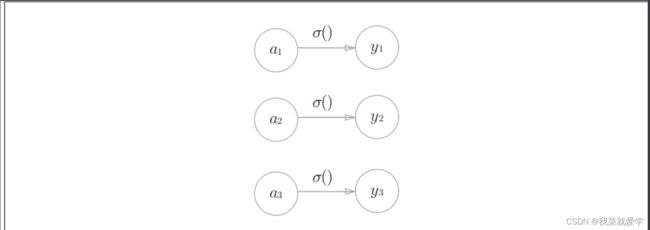
神经网络分别用在分类问题和回归问题上，根据自己所需改变输出层的激活函数。通常回归问题用恒等函数，回归问题是根据某个输入预测一个数值的问题，如根据一个人的图像预测这个人的体重的问题。分类问题用softmax函数，分类问题是数据属于哪一个类别的问题，如区分图像中的人是男性还是女性。

5.1 恒等函数

恒等函数会将输入按原样输出，对于输入的信息，不加以任何改动地直接输出。

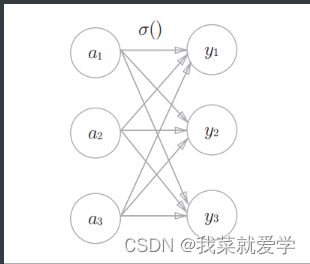
5.2 softmax函数

分类问题使用softmax函数，如下列式子。exp(x)是表示e(x)的指数函数(e=2.7182…)。假设输出层有n个神经元，计算第k个神经元的输出y(k)。softmax函数的分子是输入信号a(k)的指数函数，分母是所有输入信号的指数函数的和。

a=np.array([0.3,2.9,4.0])
exp_a=np.exp(a)
print(exp_a)
# [ 1.34985881 18.17414537 54.59815003]
sum_exp_a=np.sum(exp_a)
print(sum_exp_a)
# 74.1221542101633
y=exp_a/sum_exp_a
print(y)
# [0.01821127 0.24519181 0.73659691]

1）softmax函数的缺陷

由于softmax函数的实现是要进行指数函数的运算，指数函数的运算结果很大，造成溢出，返回一个无穷大的inf。

a=np.array([1010,1000,990])
y=np.exp(a)/np.sum(np.exp(a))
print(y)
#得到
#[nan nan nan]

2）改进softmax函数

说明：对于如下式子，分子分母都乘上C这个任意的常数，任何把C移动到指数函数(exp)中，即logC。logC即为常数，用C’代替。也就是说在进行softmax函数运算的时候，加速（减去）某个常数并不会改变运算的结果。C’一般取输入信号的最大值。

c=np.max(a)
print(c)
y1=np.exp(a-c)/np.sum(np.exp(a-c))
print(y1)
# [9.99954600e-01 4.53978686e-05 2.06106005e-09]

3）softmax函数的特性

a=np.array([0.3,2.9,4.0])
b=np.array([0.03,29,0.4])
y=sofamax(a)
y1=sofamax(b)
print(y)
print(np.sum(y))
'''
[0.01821127 0.24519181 0.73659691]
1.0
'''
print(y1)
print(np.sum(y1))
'''
[2.62113180e-13 1.00000000e+00 3.79470324e-13]
1.0
'''

如上所示，softmax函数输出是0.0-1.0之间的实数。且softmax函数的输出值的总和是1。如上述y的输出结果可以清楚的看出，y[0]的概率为1.8%，y[1]的概率为24.5%，y[2]的概率为73.7%。也可以这样理解，有三个类别，有74%的概率属于第2个类别，有25%的概率属于第1个类别，有1%的概率属于第0个类别。

5.3 输出层的神经元数量

对于输出层的神经元数量需要根据具体的情况来判断。也就是说对于分类问题，输出层的神经元数量一般设定为类别的数量。如接下来手写数字识别的项目中，就是将输出层是神经元数量定义为0到9.