动态规划(一)
前言:动态规划(DP)是运筹学的一个分支,是将决策不断最优化的求解过程。动态规划算法与分治法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解中得到原问题的解。与分治法不同的是,适合于用动态规划求解的问题,经分解得到的子问题往往不是互相独立的。若用分治法来解这类问题,则分解得到的子问题数目太多,有些子问题被重复计算了很多次。如果我们能够保存已解决的子问题的答案,而在需要时再找出已求得的答案,这样就可以避免大量的重复计算,节省时间。
目录
1、动态规划题型总结
2、例题
2.1 最值问题
2.2 计数问题
2.3 存在性问题
1、动态规划题型总结
下面三种类型的题目可以使用动态规划算法求解:①最值问题;②计数问题;③存在性问题。动态规划算法一般可以分4步完成:
第一步:确定状态(最后一步+子问题);
第二步:转移方程;
第三步:初始条件和边界情况
第四步:计算顺序(多数是从小到大计算)
下面通过三个例题分别讲解如何用动态规划算法解决这三种类型的题目。
2、例题
2.1 最值问题
【题目1】有三种硬币,分别面值2元,5元和7元,每种硬币都有足够多,买一本书需要27元,如何用最少的硬币组合正好付清,不需要对方找钱。
【解决方案】第一步:确定状态(最后一步+子问题)
虽然我们不知道最优策略是什么,但是可以肯定的是该最优策略中的k枚硬币的面值加起来等于27,所以一定有一枚最后的硬币![]() ,除了这枚硬币,前面硬币的面值加起来等于
,除了这枚硬币,前面硬币的面值加起来等于![]() 。
。
关键点1:我们不关心前面的![]() 枚硬币是怎样拼出
枚硬币是怎样拼出![]() 的,而且我们现在甚至还不知道
的,而且我们现在甚至还不知道![]() 和
和![]() 的具体值,但是我们确定前面的所有硬币拼出了
的具体值,但是我们确定前面的所有硬币拼出了![]() 。
。
关键点2:因为是最优策略,所以拼出![]() 的硬币数一定是最少的,否则就不是最优策略了。
的硬币数一定是最少的,否则就不是最优策略了。
综上,子问题就变为:令![]() ,f(X)=最少用多少枚硬币拼出X。我们虽然还不知到最后一枚硬币
,f(X)=最少用多少枚硬币拼出X。我们虽然还不知到最后一枚硬币![]() 是多少,但可以确定
是多少,但可以确定![]() 只能是2,5,7
只能是2,5,7
1)若![]() ,
,![]()
2)若![]() ,
,![]()
3)若![]() ,
,![]()
因为要求最少的硬币数,所以:
![]()
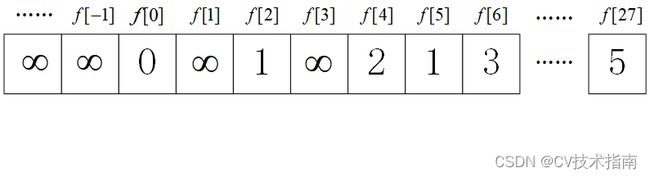
第二步:转移方程(创建数组,用来记录已求解子问题的答案,就是将前面的()变成[])
设状态f[X]=最少用多少枚硬币拼出X,对于任意X,有:
![]()
第三步:初始条件和边界情况
在这一步,我们需要思考两个问题:X-2,X-5或X-7小于0怎么办?什么时候停下来?
定义如果![]() ,就令
,就令![]() ,举个例子:
,举个例子:
![]() ,表示拼不出1。
,表示拼不出1。
另外,初始条件![]()
第四步:计算顺序
本题语境下采用从小到大的计算顺序,其优势就是当计算到f[X]时,f[X-2]、f[X-5]和f[X-7]都已经知道结果了。
分析完了解题思路,上代码:
public class Demo {
//测试代码
public static void main(String[] args) {
int r;
int[] A = {2, 5, 7};
r =coinChange(A, 27);
System.out.println(r);
}
//DP算法部分
public static int coinChange(int[] A, int M) {
int n = A.length;
int[] f = new int[M + 1];
int i, j;
f[0] = 0;
for (i = 1; i <= M; i++) {
f[i] = Integer.MAX_VALUE;
for (j = 0; j < n; j++) {
if (i >= A[j] && f[i - A[j]] != Integer.MAX_VALUE && f[i - A[j]] + 1 < f[i]) {
f[i] = f[i - A[j]] + 1;
}
}
}
if (f[M] == Integer.MAX_VALUE) {
return -1;
} else {
return f[M];
}
}
}2.2 计数问题
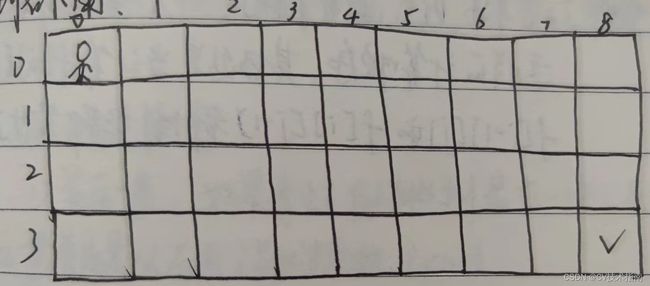
【题目2】给定m行n列的网格,有一个机器人从左上角(0,0)出发,每次只能向下或向右走一步,问有多少种不同的方式走到右下角?
【解决方案】 第一步:确定状态
①最后一步:右下角的坐标为![]() ,那么前一步机器人一定是在
,那么前一步机器人一定是在![]() 或者
或者![]() 。如果有
。如果有![]() 种方式到达
种方式到达![]() ,有
,有![]() 种方式到达
种方式到达![]() ,则有
,则有![]() 种方式可以到达
种方式可以到达![]() 。
。
②子问题:有多少种方式可以走到![]() 和有多少种方式可以走到
和有多少种方式可以走到![]()
第二步:转移方程
![]()
第三步:初始条件和边界情况
①初始条件: f[0][0]=1,定义机器人只有一种方式到左上角,就是不动。
②边界情况:如果i=0或j=0,则此时前一步只能由一个方向走过来,即f[0][j]=1,f[i][0]=1
第四步:计算顺序
先算第0行,再算第1行,……,最后算最后一行,每行中从左到右计算。这样的计算顺序其优势是当计算f[i][j]时,f[i-1][j]和f[i][j-1]都刚好计算过了。
代码实现如下:
public class Demo {
public static void main(String[] args) {
int r=uniquePaths(6,6);
System.out.println(r);
}
public static int uniquePaths(int m, int n) {
int[][] f = new int[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (i == 0 || j == 0) {
f[i][j] = 1;
} else {
f[i][j] = f[i - 1][j] + f[i][j - 1];
}
}
}
return f[m - 1][n - 1];
}
}
2.3 存在性问题
【题目3】有n块石头分别在x轴的0,1,2,……,n-1位置上,一只青蛙在石头0,想跳到石头n-1, 假设青蛙在第i块石头上最多可以向前跳距离![]() ,请问青蛙能否跳到石头n-1上?
,请问青蛙能否跳到石头n-1上?
【解决方案】第一步:确定状态
①最后一步:如果青蛙能跳到最后一块石头n-1上,那么最后一步肯定是从石头i跳过来的,其中![]()
②子问题:原问题就转化为青蛙能不能跳到石头i上
第二步:转移方程
设![]() 表示青蛙能不能跳到石头
表示青蛙能不能跳到石头![]() 上,
上,
![]()
上式表示遍历所有可能的石头,能跳到石头j必须满足两个条件:1)能跳到石头i上;2)能从石头i跳到石头j上。
第三步:初始条件和边界情况
![]() ,因为一开始青蛙就在石头0上,无边界情况
,因为一开始青蛙就在石头0上,无边界情况
第四步:计算顺序
先计算f[1],在计算f[2],……,最后计算f[n-1]
代码实现如下:
public class Demo {
public static void main(String[] args) {
int[] A = {2, 3, 1, 1, 4};
boolean r = jump(A);
System.out.println(r);
}
public static boolean jump(int[] A) {
if (A == null || A.length == 0) {
return false;
}
int n = A.length;
boolean[] f = new boolean[n];
f[0] = true;
for (int j = 0; j < n; j++) {
for (int i = 0; i < j; i++) {
if (f[i] && i + A[i] >= j) {
f[j] = true;
break;
}
}
}
return f[n - 1];