隐马尔可夫模型HMM笔记——HMM原理介绍、python hmmlearn库的使用

隐马尔可夫模型HMM是序列标注模型最基础的一种，由字构词是序列标注模型的一种应用。序列标注指的就是给定一个序列x=x1x2…xn，找出序列中每个元素对应标签y=y1y2…yn，其中y所有可能的取值集合称为标注集（在NLP，x通常是字符或词语，y则是待预测的组词角色或词性等标签）。例如，输入一个自然数序列，输出它们的奇偶性。

中文分词、词性标注以及命名实体识别，都可以转化为序列标注问题。

本文按照隐马尔可夫模型需要的理论来逐步讲解HMM，基础知识（比如随机过程）大概理解一下就好，因为理论知识是循序渐进的，如果跳过了前面的铺垫知识后面理解不了的话，可以再跳回来看一下。

一、隐马尔可夫模型理论知识

1. 随机过程

其实简单理解就是随着时间t的发展，检测到的一系列值X(t)。

随机过程中有平稳随机过程，马尔可夫随机过程。

2. 平稳随机过程

 类似于某一时间段的分布函数和另一时间段的分布函数是一样的。

3. 隐马尔可夫模型的两个假设前提

我删去了原本的隐马尔可夫模型的描述，这里用自己的语言尝试去描述这个模型。

隐马尔可夫模型常用作序列标注类的问题。这里首先提出一个问题，它是如何用某一模型去描述序列标注的问题呢？

我们思考一下序列标注是做什么的，它是把一个句子中所有的词都标注上词性之类的tag，像是NER（命名实体识别）的话，就是把一个句子中所有的词分类成人物、地点、时间之类的tag。所以我们可以简化描述一下，就是把一个句子中的词都打上它所属的tag。

那么在HMM中认为，某一句话的产生，是由其背后一个个tag所确定的。比如说一句话“我 在 上海”，背后就是由“人称代词 介词 名词”决定的，如果换成“名词 介词 名词”，那可能会产生“书 在 上海”这种句子，但是产生不了“我 在 上海”这类句子了

这是HMM的一个基本框架，在这个基础之上，我们还需要其他的一些限定：这就是必须要记住的HMM的两个假设前提。

隐马尔可夫模型的两个假设前提：

假设一：当前状态Yt仅仅依赖于前一个状态Y(t-1)，连续多个状态构成隐马尔可夫链y；

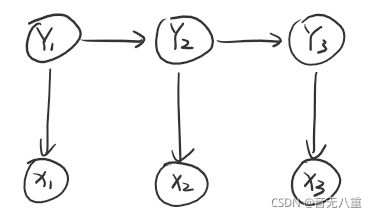
假设二：任意时刻的观测x只依赖于该时刻的状态Yt，与其他时刻的状态或观测独立无关。用箭头表示事件的依赖关系（箭头终点是结果），则隐马尔可夫模型可表示为下图：

这两个假设前提的意思就是说，对于每个隐含状态y，只有前一个隐含状态影响当前隐含状态，而每个观测状态x仅由对应的隐含状态y决定，并不受其他隐含状态的影响。

这里隐含状态就可以理解成tag标签序列，而观测状态就是“我 在 上海”这类的输出。隐含状态之所以叫隐含就是因为词性之类的tag是我们所看不见、观测不到的，我们直接看到的是观测序列。

对于接下来的关于HMM的一系列概念，我这里参考知乎上的回答的例子，用骰子来形象的举例。

4. 隐马尔科夫模型的马尔可夫链、隐含序列、观测序列、转移概率、输出概率

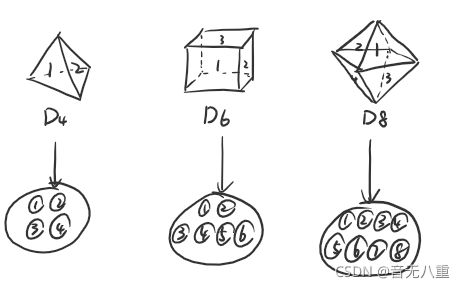
我们假设有三个骰子，骰子D6是六面体，骰子D4是四面体，骰子D8是八面体（如下图）：

D4骰子有可能产生的数字是1~4，每个数字产生的概率都是1/4；

D6骰子有可能产生的数字是1~6，每个数字产生的概率都是1/6；

D8骰子有可能产生的数字是1~8，每个数字产生的概率都是1/8。

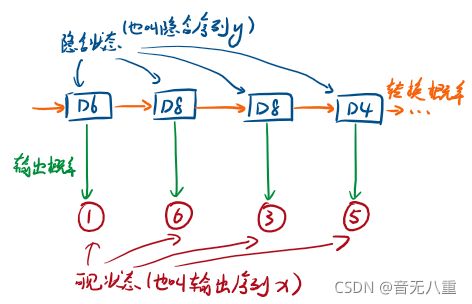
我们投骰子10次，每次都要先选择骰子（即每个骰子被选择的概率为1/3），选择骰子时我们假设当前选择的骰子只受上一个骰子的影响，这就是转移概率。然后投骰子。假设我们投了10次后的得到的数字为：1 6 3 5 2 7 3 5 2 4，那么这就是可见序列（也叫可见状态链）。

在这个例子里，隐含序列（也叫隐含状态链）就是用的骰子的序列：D6 D8 D8 D6 D4 D8 D6 D6 D4 D8。

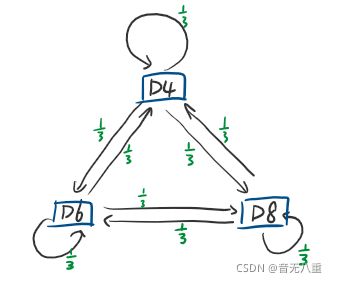
一般HMM中说到的马尔可夫链其实就是隐含状态链，因为隐含状态存在转换概率，本例子中每个骰子被转换到的概率都是1/3（那么实际上也可以是不平均的概率值）（上图）。（马尔可夫链实际上就是一个有向图，所以马尔可夫模型也所属于图模型中的有向图模型的动态贝叶斯网络的分类）

每个骰子在被选择后，它的输出会有很多种可能性，比如骰子D4输出1的可能性是1/4，输出2的可能性也是1/4，某一隐含状态到可见状态之间有一个概率叫输出概率，就是指的这个概率。

总的HMM模型如下图：

 

 5. HMM模型表达

HMM可以用五个元素来描述{S,O,π,,}，包括2个状态集合和3个概率矩阵：

（1）隐含状态S

这些状态之间满足马尔可夫性质，是马尔可夫模型中实际所隐含的状态。这些状态通常无法通过直接观测得到。（就像4中的D6 D8…）

（2）可观测状态O

在模型中与隐含状态相关联，可通过之间观测得到。

（注：可观测状态数目不一定要和隐含状态数目一致）

（3）初始状态概率矩阵

表示隐含状态在初始时刻t=1时的概率矩阵。

（4）隐含状态转移概率矩阵A

描述了HMM模型中各个状态之间的转移概率。

=, 1≤,≤

表示在t时刻、状态为Si条件下，在t+1时刻状态是Sj的概率。

（5）观测状态转移概率矩阵B

（英文名为Confusion Matrix，直译混淆矩阵）

令N代表隐含状态数目，M代表可观测状态数目，则：

=, 1≤≤, 1≤≤

表示在t时刻、隐含状态是Sj条件下，观察状态为Oi的概率。（那应该就是4中提到的输出概率了，选定骰子，投出某数字Oi的概率）

通常情况下，可以用λ=(,,)三元组来简洁表示一个隐马尔可夫模型。

6. HMM的三个问题

（1）评估问题（概率问题）：前向算法

（2）解码问题：Viterbi算法

（3）学习问题：Baum-Welch算法（向前向后算法）

（1）评估问题

简单版解释：给定模型参数和X，给出X可能出现的概率。

详细版解释：给定观测序列O=123…和模型参数λ=(,,)，怎样有效计算某一观测序列的概率，进而对该HMM作出相关评估。通常是利用forward算法分别计算每个HMM产生给定观测序列O的概率，然后从中选出最优的HMM模型。

经典例子：语音识别。每个单词生成一个对应的HMM，每个观测序列由一个单词的语音构成，单词的识别是通过评估进而选出最有可能产生观测序列所代表的读音的HMM实现。

（2）解码问题

简单版解释：给定模型参数和X，给出最有可能的隐含序列Y。

详细版解释：给定观测序列O=123…和模型参数λ=(,,)，怎样寻找某种意义上最优的隐状态序列。在这类问题中，我们更加关注的是 马尔可夫模型中的隐含状态，通常利用Viterbi算法（一种动态规划算法）来寻找。

经典例子：中文分词，即如果划分一个句子的构成。句子的分词方法可以看成是隐含状态，而句子可以看成是给定的可观测状态，从而通过建立HMM来寻找最可能正确的分词方法。

（3）学习问题

即HMM的模型参数λ=,,未知，如何调整这些参数以使观测序列O=123…的概率尽可能的大。通常使用Baum-Welch算法以及Reversed Viterbi算法解决。

HMM的学习过程就是在学习两个概率矩阵A和B（按照4中的定义，大小分别为N*N，M*N）

二、HMM实现（调用python第三方库：hmmlearn）

1. HMM常用的三种模型：  

1.GaussianHMM 观测状态连续型且符合高斯分布  
2.GMMHMM 观测状态连续型且符合混合高斯分布  
3.MultinomialHMM 观测状态离散型  

2. 隐马可夫模型参数设置，属性设置，模型函数

模型参数：  
n_components : 隐藏状态数目  
covariance_type: 协方差矩阵的类型  
min_covar : 最小方差，防止过拟合  
startprob_prior : 初始概率向量  
transmat_prior : 转移状态矩阵  
means_prior, means_weight : 均值  
covars_prior, covars_weight : 协方差  
algorithm : 所用算法  
random_state : 随机数种子  
n_iter : 最大迭代次数  
tol : 停机阈值  
verbose : 是否打印日志以观察是否已收敛  
params : 决定哪些参数在迭代中更新  
init_params : 决定哪些参数在迭代前先初始化  

模型属性:  
n_features：n维高斯分布  
monitor_：收敛监测  
transmat_：转移矩阵  
startprob_：初始向量  
means_：均值  
covars_：方差  

模型常用函数调用:  
decode(X, lengths=None, algorithm=None)，返回最可能的隐藏状态  
sample(n_samples=1, random_state=None)， 随机生成一个模型的Z和X  
fit(X, lengths=None) ，估计模型参数  
predict(X, lengths=None) ，预测最可能的隐藏状态 
predict_proba(X, lengths=None) ，预测各状态的概率  
score(X, lengths=None) ，当前模型下出现X的概率  

3. MultinomialHMM使用实例

import numpy as np
from hmmlearn import hmm
import math

#代码在jupyter notebook上运行，print之类的语法可能不同

#from IPython.core.interactiveshell import InteractiveShell
#InteractiveShell.ast_node_interactivity = 'all'

#隐藏状态(2个)
states = ['Rainy','Sunny']
n_states = len(states)   #长度

#可观察状态(3个)
observations = ['walk','shop','clean']
n_observations = len(observations)

#初始转移概率矩阵pai（隐藏状态有俩，所以矩阵shape=（1，2））
start_probability = np.array([0.6,0.4])

#状态转移矩阵A（矩阵shape=（2，2））
transition_probability = np.array([
    [0.7,0.3],
    [0.4,0.6]
])

#观测状态转移矩阵B（每个状态有3种可观察状态，所以矩阵shape=（2，3））
emission_probability = np.array([
    [0.1,0.4,0.5],
    [0.6,0.3,0.1]
])

#构建了一个MultinomialHMM模型，模型包括开始的转移概率、转移矩阵A和B
model = hmm.MultinomialHMM(n_components=n_states)
model.startprob_ = start_probability
model.transmat_ = transition_probability
model.emissionprob_ = emission_probability

#给出一个可见序列
bob_Actions = np.array([[2,0,1,1,2,0]]).T

#解决问题1：解码问题——已知模型和X，估计最可能的Z（Vertibi算法）
logbrop, weathers = model.decode(bob_Actions,algorithm="viterbi")   #输出是拟合评价，预测结果
print("Bob Actions:"+",".join(map(lambda x:observations[x],bob_Actions.T.reshape(-1))))    #把bob_Actions中的元素都转换成对应的状态词  
print("weathers:"+", ".join(map(lambda x: states[x], weathers)))
print(logbrop)    #反映模型拟合的好坏，数值越大越好

#解决问题2：概率问题——已知模型参数和X，估计X出现的概率
score = model.score(bob_Actions,lengths=None)
print(score)       ##其实真正的概率是以自然数e为底数ln(P) = -6.892170869,所以概率P = 0.00101570648021
print("概率为："+str(math.exp(score)))

#解决问题3：学习问题——仅给出X，估计模型参数，Baum-Welch算法（实际上是基于EM算法的求解）
# 解决这个问题需要X的有一定的数据量，然后通过model.fit(X, lengths=None)来进行训练然后自己生成一个模型
# 并不需要设置model.startprob_,model.transmat_,model.emissionprob_
states = ["Rainy", "Sunny"]##隐藏状态
n_states = len(states)##隐藏状态长度
  
observations = ["walk", "shop", "clean"]##可观察的状态
n_observations = len(observations)##可观察序列的长度
  
model = hmm.MultinomialHMM(n_components=n_states, n_iter=1000, tol=0.01)  #设置模型，和前两点不一样的就是设置训练轮数和阈值
  
X = np.array([[2, 0, 1, 1, 2, 0],[0, 0, 1, 1, 2, 0],[2, 1, 2, 1, 2, 0]])
model.fit(X)
print(model.startprob_)
print(model.transmat_)
print(model.emissionprob_)

# 可以进行多次fit,然后拿评分最高的模型，就可以预测了
print("predict:")
# 预测最可能的隐藏状态
print(model.predict(bob_Actions, lengths=None))

# 预测各个隐藏状态的概率
print("probability:")
print(model.predict_proba(bob_Actions, lengths=None))

# 在生成的模型中，可以随机生成随机生成一个模型的Z和X
X,Z = model.sample(n_samples=5, random_state=None)
print("Bob Actions:", ", ".join(map(lambda x: observations[x], X.T.reshape(-1))))
print("weathers:", ", ".join(map(lambda x: states[x], Z)))

本文就是在参考各个文章学习后，自己总结整合的学习笔记，因此也仅作笔记用。具体参考的内容链接如下：

深度学习 --- 受限玻尔兹曼机RBM（马尔科夫过程、马尔科夫链）

如何用简单易懂的例子解释隐马尔可夫模型？

隐马尔可夫模型

隐马尔科夫模型模型：原理、实现