RANSAC算法理解

RANSAC是“RANdom SAmple Consensus（随机抽样一致）”的缩写。它可以从一组包含“局外点”的观测数据集中，通过迭代方式估计数学模型的参数。它是一种不确定的算法——它有一定的概率得出一个合理的结果；为了提高概率必须提高迭代次数。

RANSAC的基本假设是： 
（1）数据由“局内点”组成，例如：数据的分布可以用一些模型参数来解释； 
（2）“局外点”是不能适应该模型的数据； 
（3）除此之外的数据属于噪声。 
局外点产生的原因有：噪声的极值；错误的测量方法；对数据的错误假设。 
RANSAC也做了以下假设：给定一组（通常很小的）局内点，存在一个可以估计模型参数的过程；而该模型能够解释或者适用于局内点。

一、示例 

一个简单的例子是从一组观测数据中找出合适的2维直线。假设观测数据中包含局内点和局外点，其中局内点近似的被直线所通过，而局外点远离于直线。简单的最小二乘法不能找到适应于局内点的直线，原因是最小二乘法尽量去适应包括局外点在内的所有点。相反，RANSAC能得出一个仅仅用局内点计算出模型，并且概率还足够高。但是，RANSAC并不能保证结果一定正确，为了保证算法有足够高的合理概率，我们必须小心的选择算法的参数。 
 

 

 二、概述

RANSAC算法的输入是一组观测数据，一个可以解释或者适应于观测数据的参数化模型，一些可信的参数。 
RANSAC通过反复选择数据中的一组随机子集来达成目标。被选取的子集被假设为局内点，并用下述方法进行验证： 
1.首先我们先随机假设一小组局内点为初始值。然后用此局内点拟合一个模型，此模型适应于假设的局内点，所有的未知参数都能从假设的局内点计算得出。 
2.用1中得到的模型去测试所有的其它数据，如果某个点适用于估计的模型，认为它也是局内点，将局内点扩充。 
3.如果有足够多的点被归类为假设的局内点，那么估计的模型就足够合理。 
4.然后，用所有假设的局内点去重新估计模型，因为此模型仅仅是在初始的假设的局内点估计的，后续有扩充后，需要更新。 
5.最后，通过估计局内点与模型的错误率来评估模型。 
整个这个过程为迭代一次，此过程被重复执行固定的次数，每次产生的模型有两个结局： 
1、要么因为局内点太少，还不如上一次的模型，而被舍弃， 
2、要么因为比现有的模型更好而被选用。
 

三、算法

伪码形式的算法如下所示： 
输入： 
data —— 一组观测数据 
model —— 适应于数据的模型 
n —— 适用于模型的最少数据个数 
k —— 算法的迭代次数 
t —— 用于决定数据是否适应于模型的阀值 
d —— 判定模型是否适用于数据集的数据数目 
输出： 
best_model —— 跟数据最匹配的模型参数（如果没有找到好的模型，返回null） 
best_consensus_set —— 估计出模型的数据点 
best_error —— 跟数据相关的估计出的模型错误
 

iterations = 0
best_model = null
best_consensus_set = null
best_error = 无穷大
while ( iterations < k )
maybe_inliers = 从数据集中随机选择n个点
maybe_model = 适合于maybe_inliers的模型参数
consensus_set = maybe_inliers

for ( 每个数据集中不属于maybe_inliers的点 ）
if ( 如果点适合于maybe_model，且错误小于t ）
将点添加到consensus_set
if （ consensus_set中的元素数目大于d ）
已经找到了好的模型，现在测试该模型到底有多好
better_model = 适合于consensus_set中所有点的模型参数
this_error = better_model究竟如何适合这些点的度量
if ( this_error < best_error )
我们发现了比以前好的模型，保存该模型直到更好的模型出现
best_model =  better_model
best_consensus_set = consensus_set
best_error =  this_error
增加迭代次数
返回 best_model, best_consensus_set, best_error

 

RANSAC算法的可能变化包括以下几种： 
（1）如果发现了一种足够好的模型（该模型有足够小的错误率），则跳出主循环。这样可能会节约计算额外参数的时间。 
（2）直接从maybe_model计算this_error，而不从consensus_set重新估计模型。这样可能会节约比较两种模型错误的时间，但可能会对噪声更敏感。

其实核心就是随机性和假设性。随机性用于减少计算了，那个循环次数就是利用正确数据出现的概率。所谓的假设性，就是说随机抽出来的数据我都认为是正确的，并以此去计算其他点，获得其他满足变换关系的点，然后利用投票机制，选出获票最多的那一个变换。
 

四、优点与缺点 

RANSAC的优点是它能鲁棒的估计模型参数。例如，它能从包含大量局外点的数据集中估计出高精度的参数。RANSAC的缺点是它计算参数的迭代次数没有上限；如果设置迭代次数的上限，得到的结果可能不是最优的结果，甚至可能得到错误的结果。RANSAC只有一定的概率得到可信的模型，概率与迭代次数成正比。RANSAC的另一个缺点是它要求设置跟问题相关的阀值。 
RANSAC只能从特定的数据集中估计出一个模型，如果存在两个（或多个）模型，RANSAC不能找到别的模型。
 

 五、应用

1） 三维点云处理中的模型提取，比如直线、球、圆柱、平面等的拟合与分割。常用到RANSC算法。

点云配准中的粗配准阶段：（一般粗配准之后还需要ICP精配准）

采样一致性初始配准算法（Sample Consensus Initial Aligment , SAC-IA)  此算法依赖于点特征直方图，所以在执行此算法之前，应该先计算点云的FPFH，算法的大致思路如下：

 (1) 从待配准点云P中选取n个采样点，为了尽量保证所采样的点具有不同的FPFH特征，采样点两两之间的距离应满足大于预先给定最小距离阈值d。

 (2) 在目标点云Q中查找与点云P中采样点具有相似FPFH特征的一个或多个点，从这些相似点中随机选取一个点作为点云P在目标点云Q中的一一对应点。

 (3) 计算对应点之间刚体变换矩阵, 然后通过求解对应点变换后的“距离误差和”函数来判断当前配准变换的性能。此处的距离误差和函数多使用Huber罚函数表示， 记为：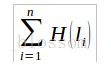

其中：

式中：mi为一预先给定值，li为第i组对应点变换之后的距离差。上述配准的最终目的是在所有变换中找到一组最优的变换，使得误差函数的值最小，此时的变换即为最终的配准变换矩阵，进一步可得到配准结果。  SAC-IA得到的变换矩阵不精确，所以它只能用于粗配准，在PCL库中的registration模块可实现SAC-IA算法。  在点数量较多时，计算FPFH特征较慢，使得SAC-IA算法效率很低，此时，需要先对点云进行下采样处理，以减少点的数量，但这会造成部分特征点丢失，使得配准准确度降低。
 

2）解决误匹配的问题。

RANSAC算法经常用于计算机视觉，例如同时求解相关问题与估计立体摄像机的基础矩阵，在图像拼接时求变换矩阵的时候。

利用到SLAM中，经常被用于滤除误匹配。