Sloan中性群落模型(NCM)推断群落构建原理及其R实现
目录
-
-
- 1.中性理论原理介绍
- 2. R语言实现
- 3. 参考文献
- 4. 其它推断群落构建的方法
- 5. 测试文件与R代码及运行效果
-
许多SCI文章都使用了一种叫NCM的方法来对微生物群落构建(中性理论 or 生态位理论?)进行预测,本文将对NCM的实现原理及其R实现做介绍。在介绍其原理的过程中会有一些数学公式,不要对这些数学公式产生抵触情绪,我会解释其每一项的生态学含义。与原理相比,其R实现则相对简单,阅读完后可将原理与R实现进行对比。
1.中性理论原理介绍
In order for an assemblage to change, an individual must die or leave the system. It is then immediately replaced by an individual either by a birth from within the community or by an immigrant from a source community
只有当物种死亡或离开这个系统时,群落结构才会发生改变。此时,离开个体的生态位就会空余出来,其它个体会通过来自群落外的迁移或群落内部的繁殖来填补空出的生态位。因此可以把群落的动态描述为死亡——繁殖/扩散——死亡这样的循环。
根据上述的原理,如果我知道 t0 时刻:
- 物种 i 的在本地群落(local community)内的个体数为 N i N_i Ni ,即OTU table(行名:sample ID,列名:species ID)中的每个单元格的数字。
- 物种 i 在宏群落(meta-community)内的相对丰度为 p i p_i pi,即OTU table中列的和/OTU表的和
- 该本地群落(local community)总的个体数为 N T N_T NT,即OTU table中行的和
- 个体死亡后被宏群落中的物种替换的概率为 m m m
- 物种 i 的繁殖率与所有物种的平均繁殖率的比值 α i \alpha_i αi
当群落中1个个体(individual)死亡时,我们记此时的时间为 t1。此时会有以下几种可能:
- 可能1: 死亡的是物种 i 。其概率为: N i / N T N_i/N_T Ni/NT
- 可能1.1: 物种 i 的个体死亡后空余的生态位被群落内的物种通过繁殖的方式取代。其概率为: 1 − m 1-m 1−m
- 可能1.1.1: 被群落内相同的物种取代。其概率为: ( 1 + α i ) ( N i − 1 ) / ( N T − 1 ) (1+\alpha_i)(N_i-1)/(N_T - 1) (1+αi)(Ni−1)/(NT−1)
- 可能1.1.2: 被群落内不相同的物种取代。其概率为: ( 1 − α i ) ( N T − N i ) / ( N T − 1 ) (1-\alpha_i)(N_T - N_i)/(N_T - 1) (1−αi)(NT−Ni)/(NT−1)
- 可能1.2: 物种 i 的个体死亡后空余的生态位被群落外的物种通过扩散的方式取代。其概率为: m m m
- 可能1.2.1: 被群落外相同的物种取代。其概率为: p i p_i pi
- 可能1.2.2: 被群落外不相同的物种取代。其概率为: 1 − p i 1 - p_i 1−pi
- 可能1.1: 物种 i 的个体死亡后空余的生态位被群落内的物种通过繁殖的方式取代。其概率为: 1 − m 1-m 1−m
- 可能2: 死亡的不是物种 i。其概率为: ( N T − N i ) / N T (N_T - N_i)/N_T (NT−Ni)/NT
- 可能2.1: 非物种 i 的个体死亡后空余的生态位被群落内的物种通过繁殖的方式取代。 其概率为: 1 − m 1 - m 1−m
- 可能2.1.1: 被群落内的物种 i 取代。 ( 1 + α i ) N i / ( N T − 1 ) (1+\alpha_i)N_i/(N_T - 1) (1+αi)Ni/(NT−1)
- 可能2.1.2: 被群落内的非物种 i 取代。 ( 1 − α i ) ( N T − N i − 1 ) / ( N T − 1 ) (1-\alpha_i)(N_T - N_i - 1)/(N_T - 1) (1−αi)(NT−Ni−1)/(NT−1)
- 可能2.2: 非物种 i 的个体死亡后空余的生态位被群落外的物种通过扩散的方式取代。其概率为: m m m
- 可能2.2.1: 被群落外的物种 i 取代。 p i p_i pi
- 可能2.2.2: 被群落外的非物种 i 取代。 1 − p i 1 - p_i 1−pi
- 可能2.1: 非物种 i 的个体死亡后空余的生态位被群落内的物种通过繁殖的方式取代。 其概率为: 1 − m 1 - m 1−m
那么,与 t0 时刻相比 t1 时刻物种 i 的数量可能:减少 1个、不变和增加一个,即 t1 时刻物种 i 的数量可能为: N i − 1 N_i-1 Ni−1、 N i N_i Ni和 N i + 1 N_i+1 Ni+1,其可能的概率如下:
物种 i 增加一个的概率 = 可能2 * (可能2.1 * 可能2.1.1 + 可能2.2 * 可能2.2.1)
物种 i 不变的概率 = 可能1 * (可能1.1 * 可能1.1.1 + 可能1.2 * 可能1.2.1)+ 可能2 * (可能2.1 * 可能2.1.2 + 可能2.2 * 可能2.2.2)
物种 i 减少一个的概率 = 可能1 * (可能1.1 * 可能1.1.2 + 可能1.2 * 可能1.2.2)
写成数学表达式就是文献中的公式了:

但我认为文献中的公式有点小问题,我认为应该是下面的公式,与文献的公式有些出入,我用红色标出来了:
-
P r ( N i + 1 N i ) = ( N T − N i N T ) [ m p i + ( 1 + α i ) ( 1 − m ) ( N i N T − 1 ) Pr(\frac{N_i+1}{N_i})=(\frac{N_T-N_i}{N_T})[mp_i+(1+\alpha_i)(1-m)(\frac{N_i}{N_T-1}) Pr(NiNi+1)=(NTNT−Ni)[mpi+(1+αi)(1−m)(NT−1Ni)
-
P r ( N i N i ) = N i N T [ m p i + ( 1 + α i ) ( 1 − m ) ( N i − 1 N T − 1 ) ] + ( N T − N i N T ) [ m ( 1 − p i ) + ( 1 − α i ) ( 1 − m ) ( N T − N i − 1 N T − 1 ) ] Pr(\frac{N_i}{N_i})=\frac{N_i}{N_T}[mp_i+\textcolor{red}{(1+\alpha_i)}(1-m)(\frac{N_i-1}{N_T-1})]+(\frac{N_T-N_i}{N_T})[m(1-p_i)+\textcolor{red}{(1-\alpha_i)}(1-m)(\frac{N_T-N_i-1}{N_T-1})] Pr(NiNi)=NTNi[mpi+(1+αi)(1−m)(NT−1Ni−1)]+(NTNT−Ni)[m(1−pi)+(1−αi)(1−m)(NT−1NT−Ni−1)]
-
P r ( N i − 1 N i ) = N i N T [ m ( 1 − p i ) + ( 1 − α i ) ( 1 − m ) ( N T − N i N T − 1 ) ] Pr(\frac{N_i-1}{N_i})=\frac{N_i}{N_T}[m(1-p_i)+(1-\alpha_i)(1-m)(\frac{N_T-N_i}{N_T-1})] Pr(NiNi−1)=NTNi[m(1−pi)+(1−αi)(1−m)(NT−1NT−Ni)]
这个公式的意义就是当我们知道 t0 时刻的物种 i 的丰度时,我们就可以推断下一时刻 t1 时物种 i 的可能的数量。此时,令 x i = N i / N T x_i=N_i/N_T xi=Ni/NT,及 x i x_i xi表示物种 i 的相对丰度。根据forward Kolmogorov equation, x i x_i xi在 t 时刻的概率密度函数为: x i x_i xi的概率密度 ϕ i ( x i , t ) \phi_i(x_i,t) ϕi(xi,t)随时间 t 的变化为:
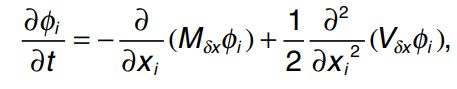
M δ x M_{\delta x} Mδx和 V δ x V_{\delta x} Vδx 中 M M M表示期望, V V V表示方差, δ x \delta x δx表示x的变化量。因此 M δ x M_{\delta x} Mδx 表示物种 i 相对丰度变化量的期望, V δ x V_{\delta x} Vδx表示物种 i 相对丰度变化量的方差。因此:
M δ x = 1 ∗ P r ( N i + 1 N i ) + ( − 1 ) ∗ P r ( N i − 1 N i ) M_{\delta x}=1 * Pr(\frac{N_i+1}{N_i})+(-1)*Pr(\frac{N_i-1}{N_i}) Mδx=1∗Pr(NiNi+1)+(−1)∗Pr(NiNi−1)
V δ x = 1 ∗ P r ( N i + 1 N i ) + 1 ∗ P r ( N i − 1 N i ) V_{\delta x}=1 * Pr(\frac{N_i+1}{N_i})+1*Pr(\frac{N_i-1}{N_i}) Vδx=1∗Pr(NiNi+1)+1∗Pr(NiNi−1)
可得:

这里 V δ x V_{\delta x} Vδx与 M δ x M_{\delta x} Mδx相比可以忽略不计,因为 N T N_T NT在OTU表中每个样点往往有成千上万条序列,即 N T > 1000 N_T>1000 NT>1000,而 0 < x i < 1 0
且 ∂ ϕ ∂ x = 0 \frac{ \partial \phi }{\partial x} = 0 ∂x∂ϕ=0,获得 ϕ i \phi_i ϕi的结果为

该分布是一个beta分布的概率密度函数。物种 i 占居的频率(occurrence frequency: row sums of binary OTU table/number of sites)为其概率密度函数的积分。
此时该分布是一个beta分布,我们就可以在R语言中利用beta分布对其进行拟合,获得参数m的评估值。
2. R语言实现
##Fits the neutral model from Sloan et al. 2006 to an OTU table and returns several fitting statistics. Alternatively, will return predicted occurrence frequencies for each OTU based on their abundance in the metacommunity
#Install the following packages if they haven't been availabled in your computer yet
library(Hmisc)
library(minpack.lm)
library(stats4)
#using Non-linear least squares (NLS) to calculate R2:
#spp: A community table with taxa as rows and samples as columns
spp<-read.csv('spp.txt',head=T,stringsAsFactors=F,row.names=1,sep = "\t")
spp<-t(spp)
#get the mean of abundance of each sample
N <- mean(apply(spp, 1, sum))
#get the mean of species relative abundance in metacommmunity
p.m <- apply(spp, 2, mean)
p.m <- p.m[p.m != 0]
#get the percentage of each species in metacommmunity
p <- p.m/N
#get the binary data of community abundance matrix
spp.bi <- 1*(spp>0)
#get the frequncy of species occurrence in metacommunity
freq <- apply(spp.bi, 2, mean)
freq <- freq[freq != 0]
#get a table record species percentage and occurrence frequency in metacommunity
C <- merge(p, freq, by=0)
#sort the table according to occurence frquency of each species
C <- C[order(C[,2]),]
C <- as.data.frame(C)
#delete rows containning zero
C.0 <- C[!(apply(C, 1, function(y) any(y == 0))),]
p <- C.0[,2]
freq <- C.0[,3]
names(p) <- C.0[,1]
names(freq) <- C.0[,1]
d = 1/N
##Fit model parameter m (or Nm) using Non-linear least squares (NLS)
m.fit <- nlsLM(freq ~ pbeta(d, N*m*p, N*m*(1 -p), lower.tail=FALSE),start=list(m=0.1))
m.fit #get the m value
m.ci <- confint(m.fit, 'm', level=0.95)
freq.pred <- pbeta(d, N*coef(m.fit)*p, N*coef(m.fit)*(1 -p), lower.tail=FALSE)
pred.ci <- binconf(freq.pred*nrow(spp), nrow(spp), alpha=0.05, method="wilson", return.df=TRUE)
# get the R2 value
Rsqr <- 1 - (sum((freq - freq.pred)^2))/(sum((freq - mean(freq))^2))
Rsqr
#data visulization
#Drawing the figure using grid package:
#p is the mean relative abundance
#freq is occurrence frequency
#freq.pred is predicted occurrence frequency
bacnlsALL <-data.frame(p,freq,freq.pred,pred.ci[,2:3])
inter.col<-rep('black',nrow(bacnlsALL))
inter.col[bacnlsALL$freq <= bacnlsALL$Lower]<-'#A52A2A'#define the color of below points
inter.col[bacnlsALL$freq >= bacnlsALL$Upper]<-'#29A6A6'#define the color of up points
library(grid)
grid.newpage()
pushViewport(viewport(h=0.6,w=0.6))
pushViewport(dataViewport(xData=range(log10(bacnlsALL$p)), yData=c(0,1.02),extension=c(0.02,0)))
grid.rect()
grid.points(log10(bacnlsALL$p), bacnlsALL$freq,pch=20,gp=gpar(col=inter.col,cex=0.7))
grid.yaxis()
grid.xaxis()
grid.lines(log10(bacnlsALL$p),bacnlsALL$freq.pred,gp=gpar(col='blue',lwd=2),default='native')
grid.lines(log10(bacnlsALL$p),bacnlsALL$Lower ,gp=gpar(col='blue',lwd=2,lty=2),default='native')
grid.lines(log10(bacnlsALL$p),bacnlsALL$Upper,gp=gpar(col='blue',lwd=2,lty=2),default='native')
grid.text(y=unit(0,'npc')-unit(2.5,'lines'),label='Mean Relative Abundance (log10)', gp=gpar(fontface=2))
grid.text(x=unit(0,'npc')-unit(3,'lines'),label='Frequency of Occurance',gp=gpar(fontface=2),rot=90)
#grid.text(x=unit(0,'npc')-unit(-1,'lines'), y=unit(0,'npc')-unit(-15,'lines'),label='Mean Relative Abundance (log)', gp=gpar(fontface=2))
#grid.text(round(coef(m.fit)*N),x=unit(0,'npc')-unit(-5,'lines'), y=unit(0,'npc')-unit(-15,'lines'),gp=gpar(fontface=2))
#grid.text(label = "Nm=",x=unit(0,'npc')-unit(-3,'lines'), y=unit(0,'npc')-unit(-15,'lines'),gp=gpar(fontface=2))
#grid.text(round(Rsqr,2),x=unit(0,'npc')-unit(-5,'lines'), y=unit(0,'npc')-unit(-16,'lines'),gp=gpar(fontface=2))
#grid.text(label = "Rsqr=",x=unit(0,'npc')-unit(-3,'lines'), y=unit(0,'npc')-unit(-16,'lines'),gp=gpar(fontface=2))
draw.text <- function(just, i, j) {
grid.text(paste("Rsqr=",round(Rsqr,3),"\n","Nm=",round(coef(m.fit)*N)), x=x[j], y=y[i], just=just)
#grid.text(deparse(substitute(just)), x=x[j], y=y[i] + unit(2, "lines"),
# gp=gpar(col="grey", fontsize=8))
}
x <- unit(1:4/5, "npc")
y <- unit(1:4/5, "npc")
draw.text(c("centre", "bottom"), 4, 1)
3. 参考文献
[1] https://github.com/Weidong-Chen-Microbial-Ecology/Stochastic-assembly-of-river-microeukaryotes
[2] Quantifying the roles of immigration and chance in
shaping prokaryote community structure
4. 其它推断群落构建的方法
- R语言并行计算beta-NTI代码和测试文件
- R语言并行计算RCbray-curtis距离
- R语言并行计算beta多样性零偏差值
5. 测试文件与R代码及运行效果
- 测试文件及代码:Sloan中性群落模型测试文件及R代码
- 运行效果:测试文件运行效果预览
- 更多R语言分析微生物生态学的资源可参考如下链接:
https://mianbaoduo.com/o/works/240342
