深度学习(十四)Reinforce Learning概述

---

前言

本文将会步入强化学习的殿堂，不过只是对强化学习进行概述，让大家对强化学习在做的事情有一个大体的认识

一、强化学习的概念

1.强化学习的定义

1. 强化学习是智能体（Agent）以“试错”的方式进行学习，通过与环境(Environment)进行交互获得的奖赏(Reward)驱动行为(Action)，目标是使智能体获得最大的奖赏。
2. 强化学习与前面所讲的监督学习有很大的不同，强化学习不需要依靠标签好的数据信息，甚至可以不需要大量的数据，强化学习通过自身学习去产生数据集，并且利用产生的数据集继续进行学习优化，找到最优的方式。
3. 强化学习中，随机性十分重要，无论在行为的选择*还是state的产生都是随机产生的，正正是因为这些随机性，Agent才有可能搜索并发现未知的动作和未知的策略

2.强化学习的总体框架

1. 首先我们可以看到一个environment，这个环境负责产生状态state(也叫观察值Observation)，我们以下围棋为例，棋盘中每一步都是一个状态，而我们将状态记为$S_n$
2. 然后我们将状态$S_n$输入到执行器Actor中 ，执行器中拥有一个处理状态的函数，负责计算出不同行为(Action)的概率，然后按照概率分布去随机选择其中一个行为去执行，也就是说即使是相同的状态输入，输出结果也不一定一样，因为它是按概率选择的(只要概率不为0都有可能被选中)，而每个被选择的行为我们记为$A_n$,我们继续以下围棋为例，这就是指下哪一步的决策
3. 我们将行为与状态归纳到一个元祖$\pi :(s_n,a_n)$，这个我们叫做这一个状态的选择策略，而这个策略$\pi$是一个概率密度函数，其中$\pi (a|s)=P(A=a|S=s)$
4. 最后我们将这个策略重新输入到Environment中，然后根据计算出其得分Reward，我们将这个奖励定义为$r_t$，并且更新新的状态$S_{n+1}$，以下围棋为例，这指的就是更新棋盘并且占优的统计

3.强化学习的步骤

1.function with unknown

这一个具有未知数的函数其实就是我们前面所说的Actor，是一个神经网络。

并且这个网络与前面所讲过的分类器是一模一样的，输入是一个像素集，中间的神经网络可以用CNN，RNN等经典神经网络来进行建模，输出是一个类似分类器的结果，通过一个softmax函数计算出一个概率分布，然后随机选择一个输出作为本次的Action

2. define loss

每执行一个action后得到一个reward值，将这些reward值全部加起来作为我们的目标函数，我们的目标就是要使这个reward值最大，这个就是强化学习的损失函数。

3.optimization

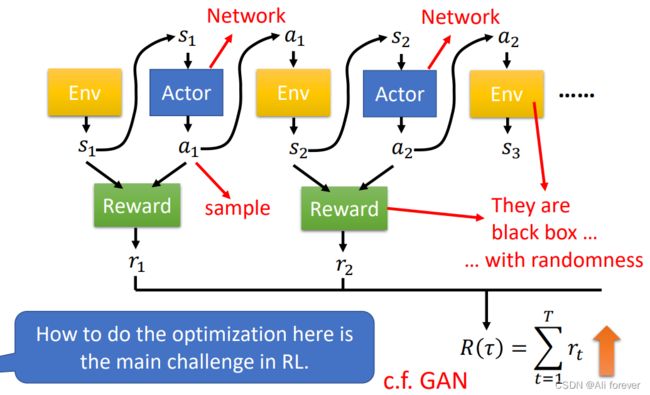
轨迹$\tau =(s_1,a_1,...,s_n,a_n)$，每一个reward都是$r_n=f(s_n,a_n)$，看上去十分类似一个RNN神经网络，但是事实上由于每一次输入相同的$s_n$，输出的$a_n$具有随机性，所以结果并不相同，大大加深了强化学习的复杂度。除此之外，environment是一个黑盒子，并不是一个神经网络，只是一个输入与输出的函数，往往也具有随机性，无法用神经网络的眼光去看待
但是可以跟生成对抗网络GAN进行比较，我们可以将Action看作生成器，而environment和reward则是判别器

4.其他重点基础概念

1. Action值函数：$Q_{\pi }(s_t,a_t)=E[U_t|S_t=s_t,A_t=a_t]$，其中这个$U_t$是奖励函数，Action值函数所表征的意义给定该策略后利用该执行器的期望得分值，如果我们的实际得分值比预期得分值要高，说明该策略是优秀的，否则就是差劣的。
2. 最优的Action值函数:$Q^{\ast }(s_t,a_t)=\underset{\pi }{\mathrm{argmax}}{Q}_{\pi }(s_t,a_t)$，这个函数表征的是最优的一个策略方式。
3. state价值函数:$V^{\pi }(s_t)=E_A[Q_{\pi }(s_t,A)]={\sum }_a\pi (a|s_t)\ast Q_{\pi }(s_t,a)$，该函数表征的是在策略$\pi$固定下状态的好坏情况，也就是快赢了还是快输了的情况。
4. reward函数:我们常用的reward函数一般为$U_t=r_1+\gamma r_2+...+{\gamma }^{n-t}{r}_n$，这样的reward函数不仅仅考虑到了后续结果对当前决策的影响，同时也注意到了后续结果对决策影响的重要性(可以看到越后前面的系数越小)，但是假设每个得分都很大时，该reward函数还需要正则化，使其有正有负，即现在还有另外一种reward函数。

二、DQN(Deep Q Network)

1.算法目的

我们上面说过，如果我们能获得最优的Action函数，那么我们在每次做决策的时候，总能十分优秀地往正确的决策方向去进行，但是事实上获取最优的Action函数是不合常理的，因为这需要我们具有预知未来的能力，很明显我们是无法做到的。
所以我们需要一个合适的方法去迫近这一个最优的Action函数，也就是我们所说的DQN，而这个迫近的神经网络为$Q(s,a;w)$

2.算法过程

首先训练出DQN，将状态$s_t$输入到DQN神经网络中，然后选出最佳的那一个行动$a_t，a_t={\mathrm{argmax}}_{a}Q(s_t,a;w)$,然后环境改变了状态得到新的状态$s_{t+1}\sim p(\cdot |s_t,a_t)$,然后循环上述过程即可

3.训练方法:基于Q-learning的TD算法

不需要对整个过程进行仿真，只需要看到一部分内容，即可以进行训练。
我们观察reward函数，发现其满足以下一个重要等式:$U_t=r_t+U_{t+1}$
TD算法满足以下这个式子$$\begin{gathered} Q(s_t,a_t;w)\approx r_t+\gamma Q(s_{t+1},a_{t+1};w) \\ =r_t+\gamma \underset{a}{\mathrm{argmax}}Q(s_{t+1},a_t;w) \end{gathered}$$$r_t$是一个真实值，并不是估计量，而Q的两项都是期望值，也就是说TD算法是用真实值与估计值去迫近估计值，我们的目标就是对$Q(s_t,a_t;w)$进行预测，获得该迫近的神经网络，从而获得最优的Action值函数

1. 首先先初始化Q函数和目标Q函数,也就是说训练的Q函数与执行的Q函数不是同一个
2. 给定状态s，基于Q采取行为a然后获取reward r和新状态s，将这些状态行为集合存放到缓冲区
3. 在缓冲区中采样状态行为集合$\{s_n,a_n\}$，然后计算目标y，更新参数去使Q函数的结果接近与y
4. 最后在每隔C步之后使目标Q函数与计算Q函数相同

4.蒙特卡罗算法

本质上就是拿观察值去近似统计量，来降低算法的复杂度或者去求解一些无法统计的统计量值，如最优价值函数中$Q^{\ast }(s_t,a_t)=E[R_t+\gamma \underset{a}{\max }{Q}^{\ast }(S_{t+1},a)]$的得分值$R_t$全部获取是不现实的，我们可以只取其中的一个观测值$r_t$即可。还有后面的那一个最优价值函数也同样只取观察值近似

三、Policy-based RL

1.算法目的

我们前面说过，策略函数的输入是状态，输出是一个概率分布，而想要获得一个最佳的输出值，需要穷尽所有的状态，才能找到最佳的Action分布
对于策略函数而言，如果状态不是有限个的(离散的)，我们就不可能一个个策略去尝试去找到最优的执行Action
所以我们需要用一个神经网络去近似我们的策略函数$\pi (a|s)$

2.算法过程

1. 我们首先将我们的策略函数转化成状态值函数，这样也就将策略的好坏转化为了状态的好坏并且结果与执行的值Action无关。
2. 我们的状态值函数的神经网络形式是$V(S;\theta )={\sum }_a\pi (a|s;\theta )\ast Q_{\pi }(s,a)$，我们只需要使状态值函数的期望最大时，则能近似得到最佳的策略函数$J(\theta )=E_S[V(S;\theta )]$
3. 随机选择其中一个状态$s_t$,然后利用蒙特卡罗算法去随机抽取一个行为$a_t$
4. 然后计算出相应的期望函数$Q_{\pi }(s_t,a_t)$，然后计算区分策略网络$d_{\theta ,t}$，最后得出策略梯度$g(a_t,{\theta }_t)$
5. 然后利用梯度上升算法去找到最佳的$\theta$值，$\theta \leftarrow \theta +\beta \frac{\partial V(S;\theta )}{\partial \theta }$

四、Action-Critic

1.算法目的

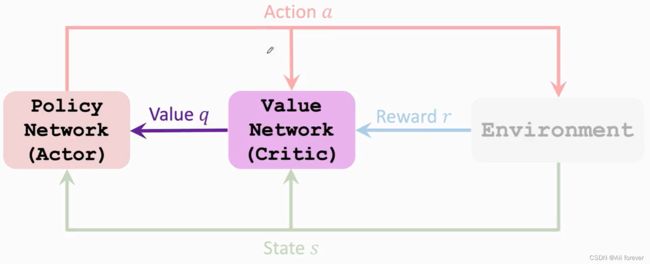
$V^{\pi }(S)={\sum }_a\pi (a|s)\ast Q_{\pi }(s,a)$中我们既不清楚策略函数也不清楚Action值函数，但如果我们用两个神经网络分别近似它们的话问题可能就能解决。
而这两个函数分别是策略网络(actor)$\pi (a|s;\theta )$和值网络(critic)$q(s,a;w)$

2.算法过程

策略网络是以值网络的好坏来作为评判标准的，值网络可以理解成裁判，会给策略网络的分布进行打分，促进网络的优化。而值网络一开始是没有任何标准的，是一个随机过程，然后以分数reward来作为根据而对评判的标准进行优化值网络。

五、No rewarding:Learning from demonstration

1.模仿学习

actor可以与environment交互，但是计算不出reward或者reward一直为0，这时候我们需要有一系列的示范数据，也就是我们模仿出的结果
当然我们会发现这与监督学习很像，因为我们也是利用人类已有的样本去进行学习去优化，但是我们会发现人类做的不一定是对的，如果纯模仿的话，就失去了强化学习的意义了。

2.inverse RL

原来我们是用reward function去推导出相应的行为action，现在我们使用收集到的示例去通过这个inverse RL去学习到这一个reward function，再去学习得到新的actor

1. 首先我们获得示范值，利用这个示范值获得的分数作为我们的teacher
2. 然后初始化actor，再每个actor里面与环境进行交互去获取新的执行集，然后重新得到一个reward函数，尽量使其优于teacher
3. 然后这个actor尝试基于这个reward函数去最大化reward值，最后输出整个系统的reward函数和actor

但事实上这就是一个生成对抗网络GAN，判别器就是teacher，生成器就是那个actor

六、近端策略优化(PPO)

1.在线策略与离线策略

1. 在线策略:需要学习的agent与输入到环境的agent是同一个agent，也就是说一边学习一边去执行任务action
2. 离线策略:需要学习的agent与输入到环境的agent不是同一个agent，这样就只需要利用一个数据集去更新，不需要每次更新一次都要重新收集数据集

2.important sampling

$$\begin{gathered} E_{x\sim p_{\theta }(x)}[f(x)]=\int f(x)p(x)dx=\int f(x)\frac{p(x)}{q(x)}q(x)dx \\ =E_{x\sim q_{\theta }(x)}[f(x)\frac{p(x)}{q(x)}] \end{gathered}$$
这样转化的原因是原函数中的分布很难获取，即使从里面随机抽取样本都极其困难，那我们就将其转化成另外一个与原概率分布很接近的分布进行计算
有了这个重要定理后，我们就可以实施我们的离线策略了，根据我们之前的累积函数，我们推导出一个新的累计函数用于输入到环境中
$$\nabla \overline{R_{\theta }}=E_{\tau \sim p_{\theta }(\tau )}[R(\tau )\nabla \log p_{\theta }(\tau )]$$
$$\nabla \overline{R_{\theta }}=E_{\tau \sim p_{\theta }^{\prime }(\tau )}[\frac{p_{\theta }(\tau )}{p_{\theta }^{\prime }(\tau )}R(\tau )\nabla \log p_{\theta }(\tau )]$$
我们要做的是利用我们假设的预估项${\theta }^{\prime }$去输入到环境中从而更新真实的项所产生的参数$\theta$
$$J^{{\theta }^{\prime }}(\theta )=E_{(s_t,a_t)\sim {\pi }_{\theta }^{\prime }}[\frac{p_{\theta }(a_t|s_t)}{p_{\theta }^{\prime }(a_t|s_t)}{A}^{{\theta }^{\prime }}(s_t,a_t)]$$
而在PPO中则加入了一个KL散度作为限制来使两个参数之间的值尽可能接近。
$$J_{PPO}^{{\theta }^{\prime }}(\theta )=J^{{\theta }^{\prime }}(\theta )-\beta KL(\theta ,{\theta }^{\prime })$$

总结

本文主要介绍了强化学习的概述，由于强化学习涉及到的方面很多，无法进入深入地讨论，只是在框架上留下印象，帮助理解强化学习的运用