数学基础知识回顾(二):集合论
集合论
- 前言
- 一、数论基础与计数基础
-
- 1.幂集
- 2.唯一析因定理(算术基本定理)
- 3.贝祖定理
- 4.同余定理
- 5.鸽巢原理(抽屉原理)
-
- 1.几个例子
- 2.一般性鸽巢原理
- 二、二元关系
-
- 1.关系及其表示
-
- 1.笛卡尔积
- 2.二元关系的定义
- 3.二元关系的一些概念
- 2.关系的性质
- 3.关系的闭包
- 4.等价关系与集合的划分
- 三、函数与映射
-
- 1.单射,满射与双射
-
- 1.定义
- 2.与关系矩阵和关系图的关系
- 3.函数的复合
- 4.几种常见函数
- 5.函数的势
- 四、偏序关系
-
- 1.定义
- 2.性质
- 3.积偏序与字典序
- 4.哈斯图
- 5.偏序集中的特殊元素
- 总结
前言
由于工业互联网通信里面图拓扑是不可避免需要讨论的一个方面,所以为了能促进后面研究的理解,本小节将会补充一些数学知识来促进我们对图拓扑的理解,而本文将不会对集合论的所有内容进行展开,而是对一些难以理解但又适用于工科数学的内容进行理解
一、数论基础与计数基础
1.幂集
假设A是集合,A的所有子集所组成的集合称作A的幂集,记作 P ( A ) = { x ∣ x ⊆ A } \mathscr{P}(A)=\{x|x\subseteq A\} P(A)={x∣x⊆A},很明显幂集里面所拥有的的元素集合数量是 2 ∣ A ∣ 2^{|A|} 2∣A∣个,其中 ∣ A ∣ |A| ∣A∣指的是集合A中元素的个数
2.唯一析因定理(算术基本定理)
设正整数 n > 1 n>1 n>1,则n可以唯一表示为 p 1 k 1 p 2 k 2 . . . p s k s p_1^{k_1}p_2^{k_2}...p_s^{k_s} p1k1p2k2...psks,其中 p 1 < p 2 . . . < p s p_1
3.贝祖定理
对不完全为0的整数 T 1 , T 2 T_1,T_2 T1,T2,存在其最大公约数 d = g c d ( T 1 , T 2 ) d =gcd(T_1,T_2) d=gcd(T1,T2),使得有整数解 m , n m,n m,n,使得方程 m T 1 + n T 2 = d mT_1+nT_2=d mT1+nT2=d成立。该定理映射了两个整数存在的一个等式关系,可以在工业互联网里面构造等式约束里面使用
4.同余定理
设n是正整数,a和b是整数,如果 n ∣ ( a − b ) n|(a-b) n∣(a−b),则一定有 a m o d n = b m o d n a \mod n =b\mod n amodn=bmodn,也就是说a与b关于n的余数相等,n被称为模,也叫同余定理,同时可以表示为 a = b + k n a=b+kn a=b+kn
引理: 若 a ≡ b ( m o d n ) , c ≡ d ( m o d n ) , 则 a c ≡ b d ( m o d n ) a \equiv b (mod \, n),c \equiv d (mod \, n),则ac \equiv bd (mod \, n) a≡b(modn),c≡d(modn),则ac≡bd(modn)
5.鸽巢原理(抽屉原理)
有n个鸽巢,如果有n+1只鸽子,则至少有一个鸽巢内有两只鸽子。
1.几个例子
- 从1,2,3,…,2n里面中任取n+1个数 a 1 , a 2 , . . . , a n + 1 a_1,a_2,...,a_{n+1} a1,a2,...,an+1,则 ∃ 1 ≤ i , j ≤ n + 1 \exists 1\leq i,j \leq n+1 ∃1≤i,j≤n+1,使得 a i ∣ a j a_i|a_j ai∣aj 或 a j ∣ a i a_j|a_i aj∣ai
证明:一个整数一定可以表示成 2 k d i 2^kd_i 2kdi,其中 d i d_i di是这个整数组里面可取到的奇数的个数,在本题里面很明显奇数的个数为n个(也就是说盒子只有n个),我们只需要利用n个盒子就能存放掉所有的苹果,题目说我们要抽n+1个数,说明至少有一个盒子里面有两个苹果,也就是可以把奇数约掉,只剩下前面的系数,而前面的系数是二的倍数,所以肯定可以整除 - 任意12个整数中一定存在两个整数,其差是11的倍数。
证明:利用前面同余定理,我们将上述描述转变为 ∃ a , b \exists a,b ∃a,b来源于12个不同的整数,使得 ( a − b ) ∣ 11 (a-b)|11 (a−b)∣11,也就是我们需要找到 a m o d 11 = b m o d 11 a\mod11=b\mod 11 amod11=bmod11,而又由于对11 求余只有11个不同的余数,而12个不同的数肯定有两个余数相等,所以得证
2.一般性鸽巢原理
设有 m 1 , m 2 . . . m n m_1,m_2...m_n m1,m2...mn个正整数,有 ∑ i = 1 n m i − ( n − 1 ) \sum_{i=1}^nm_i -(n-1) ∑i=1nmi−(n−1)个物体放在n个盒子当中,则至少对某个i而言,第i个巢中至少放了 m i m_i mi个物体
证明:假设每个盒子里面放的数量都不超过 m i m_i mi那么最多可以放的数量为 ∑ i = 1 n m i − 1 ∗ n \sum_{i=1}^nm_i-1*n ∑i=1nmi−1∗n,这个数量比原始物体要少,不成立
二、二元关系
1.关系及其表示
1.笛卡尔积
设A,B为两个集合,则笛卡尔积定义为A×B
A × B = { ( a , b ) ∣ a ∈ A 且 b ∈ B } A×B=\{(a,b)|a\in A 且b\in B \} A×B={(a,b)∣a∈A且b∈B}
笛卡尔积表示的是A的所有元素与B的所有元素两两组成的所有有序对的结合
部分性质与定理:
- 若A和B中有一个是空集,那么A×B就是空集,即 A × ∅ = ∅ × B = ∅ A×\emptyset=\emptyset×B=\emptyset A×∅=∅×B=∅
- 如果A和B都是有限集,那么A×B也是有限值,且 ∣ A × B ∣ = ∣ A ∣ × ∣ B ∣ |A×B|=|A|×|B| ∣A×B∣=∣A∣×∣B∣
2.二元关系的定义
需要原因:笛卡尔积不能表示现实中的配对关系,有一些配对情况不存在,所以需要通过定义关系来表述一些配对组,那就需要二元关系
定义:假设A,B是集合,A×B的子集R称为A到B的一个二元关系,也叫作关系。也就是说 ( a , b ) ∈ R (a,b)\in R (a,b)∈R时,称a与b具有关系R,记作 a R b aRb aRb
如果A=B,则称R为A上的一个二元关系
简单例子:集合A={张,白,宋,方},B={数据结构,离散数学,计网},而选课关系 R = { ( 张 , 计 网 ) , ( 白 , 计 网 ) , ( 宋 , 离 散 数 学 ) , ( 方 , 数 据 结 构 ) } ⊆ A × B R=\{(张,计网),(白,计网),(宋,离散数学),(方,数据结构)\}\subseteq A×B R={(张,计网),(白,计网),(宋,离散数学),(方,数据结构)}⊆A×B
几种常见关系:
- A上的恒等关系: I A = { ( a , a ) ∣ a ∈ A } I_A=\{(a,a)|a\in A\} IA={(a,a)∣a∈A}
- 幂集中的包含关系: R ⊆ = { ( x , y ) ∣ x , y ∈ P ( A ) 且 x ⊆ y } R_{\subseteq}=\{(x,y)|x,y \in \mathscr{P}(A)且x \subseteq y \} R⊆={(x,y)∣x,y∈P(A)且x⊆y}
3.二元关系的一些概念
- R的定义域 D o m ( R ) = { a ∣ a ∈ A , 存 在 b ∈ B 使 得 ( a , b ) ∈ R } Dom(R)=\{a|a\in A,存在b\in B使得(a,b)\in R\} Dom(R)={a∣a∈A,存在b∈B使得(a,b)∈R},即R中所有有序对的第一元素所构成的集合
- R的值域 R a n ( R ) = { b ∣ b ∈ B , 存 在 a ∈ A 使 得 ( a , b ) ∈ R } Ran(R)=\{b|b\in B,存在a\in A使得(a,b)\in R\} Ran(R)={b∣b∈B,存在a∈A使得(a,b)∈R},即R中所有有序对的第二元素所构成的集合
- 对于A中任一元素x,可以定义x的像集为 R ( x ) = { y ∈ B ∣ x R y } R(x)=\{y\in B|xRy\} R(x)={y∈B∣xRy}
- 而对于A中任一子集 A 1 A_1 A1,可以定义 A 1 A_1 A1的像集为 R ( A 1 ) = { y ∈ B ∣ x R y 对 某 x ∈ A 1 成 立 } R(A_1)=\{y\in B|xRy对某x\in A_1成立 \} R(A1)={y∈B∣xRy对某x∈A1成立},即 R ( A 1 ) = ⋃ x ∈ A 1 R ( x ) R(A_1)=\underset{x \in A_1}{\bigcup}R(x) R(A1)=x∈A1⋃R(x)
- R的逆: R − 1 = { ( b , a ) ∣ b ∈ B , a ∈ A , ( a , b ) ∈ R } ⊆ B × A R^{-1}=\{(b,a)|b \in B,a \in A,(a,b)\in R\}\subseteq B×A R−1={(b,a)∣b∈B,a∈A,(a,b)∈R}⊆B×A
- R和S的复合关系或合成关系:假设A、B、C是集合,R是A到B的关系,S是B到C的关系,而 S ∘ R = ( a , c ) ∣ a ∈ A , c ∈ C , 存 在 b ∈ B 使 得 ( a , b ) ∈ R 且 ( b , c ) ∈ S S\circ R ={(a,c)|a\in A,c \in C,存在b \in B使得(a,b)\in R且(b,c) \in S} S∘R=(a,c)∣a∈A,c∈C,存在b∈B使得(a,b)∈R且(b,c)∈S,复合关系具有保号性
- 假设A、B、C是集合,R是A到B的关系,S是B到C的关系,而对于A中任一子集 A 1 A_1 A1有 ( S ∘ R ) ( A 1 ) = S ( R ( A 1 ) ) (S\circ R)(A_1)=S(R(A_1)) (S∘R)(A1)=S(R(A1))
- 道路:假设A为集合, a , b ∈ A a,b\in A a,b∈A,集合A上关系R中从a到b长为n的道路是指A上的有限序列 a , x 1 , x 2 , . . . , x n − 1 , b a,x_1,x_2,...,x_{n-1},b a,x1,x2,...,xn−1,b如果满足 a R x 1 , x i R x i + 1 ( 1 ≤ i ≤ n − 2 ) , x n − 1 R b aRx_1,x_iRx_{i+1}(1\leq i \leq n-2),x_{n-1}Rb aRx1,xiRxi+1(1≤i≤n−2),xn−1Rb,则为道路n,但里面有n+1个结点
- 两个集合之间存在关系的充分条件: ( a , b ) ∈ R n (a,b)\in R^n (a,b)∈Rn,其中n为道路长度
- 关系的无穷次幂: R ∞ = ⋃ i = 1 ∞ R i R^\infty=\bigcup\limits_{i = 1}^\infty R^i R∞=i=1⋃∞Ri
2.关系的性质
- 如果 ( a , a ) ∈ R (a,a)\in R (a,a)∈R对于所有 a ∈ A a\in A a∈A都成立,则称R是自反的(也就是集合A中自己与自己有关系)
具有自反性的条件是当且仅当恒等关系是关系R的一个子集
关系图中每个顶点都有自环 - 如果 ( a , a ) ∉ R (a,a)\notin R (a,a)∈/R对于所有 a ∈ A a\in A a∈A都成立,则称R是非自反的(也就是集合A中所有元素自己与自己毫无关系)
具有非自反性的条件是当且仅当恒等关系不是关系R的一个子集
关系图中每个顶点都没有自环 - 如果对于任何 a , b ∈ A a,b\in A a,b∈A,若 ( a , b ) ∈ R (a,b)\in R (a,b)∈R必然有 ( b , a ) ∈ R (b,a)\in R (b,a)∈R都成立,则称R是对称的(对称用于描述有向还是无向)
具有对称性的条件是当且仅当关系等于关系的逆
如果两个顶点之间有边,一定是一对方向相反的边 - 如果对于任何 a , b ∈ A a,b\in A a,b∈A,若 ( a , b ) ∈ R (a,b)\in R (a,b)∈R必然有 ( b , a ) ∉ R (b,a)\notin R (b,a)∈/R都成立,则称R是非对称的
具有非对称性的条件是当且仅当关系与关系的逆相交是空集
两个顶点最多存在一条有向边,每个顶点都无自环 - 如果对于任何 a , b ∈ A a,b\in A a,b∈A,若 ( a , b ) ∈ R (a,b)\in R (a,b)∈R且 ( b , a ) ∈ R (b,a)\in R (b,a)∈R必然有 a = b a=b a=b都成立,则称R是反对称的
具有反对称性的条件是当且仅当关系与关系的逆相交是恒等关系
两个互异顶点最多存在一条有向边,每个顶点允许存在自环 - 如果对于任意 a , b , c ∈ A a,b,c\in A a,b,c∈A,若 ( a , b ) ∈ R (a,b)\in R (a,b)∈R且 ( b , a ) ∈ R (b,a)\in R (b,a)∈R必然有 ( a , c ) ∈ R (a,c)\in R (a,c)∈R都成立,则称R满足传递性
具有传递性的条件是当且仅当关系包含关系的幂
3.关系的闭包
问题引入:关系可以通过运算生成一些新的关系,但是会失去一些性质,希望通过给关系添加一些有序对让其满足特定性质,又希望添加的有序对尽可能少,以使得新的关系相差不大,引入了关系的闭包运算
定义:假设R是集合A中的关系,若存在另外一个A上的关系R’,使得满足以下性质则称为R’是R的闭包:
( 1 ) R ′ 满 足 某 些 确 定 的 性 质 ( 2 ) R ⊆ R ′ ( 3 ) 对 于 任 何 A 上 满 足 该 确 定 性 质 的 S , 如 果 R ⊆ S , 则 有 R ′ ⊆ S (1)R'满足某些确定的性质\\(2)R\subseteq R'\\(3)对于任何A上满足该确定性质的S,如果R\subseteq S,则有R'\subseteq S (1)R′满足某些确定的性质(2)R⊆R′(3)对于任何A上满足该确定性质的S,如果R⊆S,则有R′⊆S
其中1确定了新关系的性质,2确定了新关系是通过原关系添加有序对产生的,3确定了新关系包含原关系且具备该性质的最小集合
R的自反闭包为 r ( R ) r(R) r(R),对称闭包为 s ( R ) s(R) s(R),传递闭包为 t ( R ) t(R) t(R)
一些定理:
- r ( R ) = R ⋃ I A r(R)=R\bigcup I_A r(R)=R⋃IA因为满足恒等关系是该集合的一个子集
- s ( R ) = R ⋃ R − 1 s(R)=R\bigcup R^{-1} s(R)=R⋃R−1因为满足逆关系与关系都是该集合的一个子集
闭包与图的关系:
- 每个顶点如果没有自环则增加自环,得到的有向图则是该关系自反闭包的有向图
- 在关系的有向图中,如果有顶点i到顶点j的有向边且i≠j,则添加有向边(j,i)称为该关系的对称闭包的有向图,或者保留所有顶点,将有向边改为无向边,也能构造对称闭包的有向图
- 不断更新有向图,如果有顶点i到顶点j的道路,则将边(i,j)添加到有向图中直到无法添加为止,这个就能构造传递闭包的有向图
关系闭包在关系矩阵中的运算为:
- M r ( R ) = M R ∨ M I A M_{r(R)}=M_R\vee M_{I_A} Mr(R)=MR∨MIA
- M s ( R ) = M R ∨ M R − 1 M_{s(R)}=M_R\vee M_{R^{-1}} Ms(R)=MR∨MR−1
- M t ( R ) = M R ∨ M R 2 . . . ∨ M R n = M R ∨ ( M R ⊙ M R ) . . . ∨ ( M R ) ⊙ n M_{t(R)}=M_R\vee M_{R^2}...\vee M_{R^n}=M_R \vee (M_R \odot M_R)...\vee (M_R)^n_{\odot} Mt(R)=MR∨MR2...∨MRn=MR∨(MR⊙MR)...∨(MR)⊙n
4.等价关系与集合的划分
问题引入:等价关系中将具有某种共同性质的元素归并成类,从而将元素的研究转化为更简单对类的研究
定义:假设R是非空集合A的关系,那么如果R是自反的,对称的和传递的,那么我们则称R是A上的等价关系
一些性质:
- 假设R,S是两个等价关系,则 R ⋂ S R\bigcap S R⋂S也是等价关系
- 由于 R ⋃ S R\bigcup S R⋃S不一定具有传递性,但我们可以将其扩充到存在传递性,也就是说包含 R ⋃ S R\bigcup S R⋃S的最小等价关系为 ( R ⋃ S ) ∞ (R\bigcup S)^{\infty} (R⋃S)∞
- 等价类:假设R是非空集合A中的等价关系,元素 a ∈ A a \in A a∈A,集合R(a)称为a所在的等价类,记作[a];集合 { R ( a ) ∣ a ∈ A } \{R(a)|a\in A\} {R(a)∣a∈A}称作A关于R的商集,记作A/R;a是R(a)的一个代表元
集合的划分:也就是说将一个集合划分成互不相交的子集,并且这些子集的并集是原来的集合,每个集合都是一个划分块,也叫分块
划分构造等价关系:如果 π \pi π是集合A的一个划分,定义A上的关系R为aRb当且仅当a,b属于同一个划分块,那么我们称R是A中的一个等价关系
等价关系得到划分:设R是A上的一个等价关系,那么如果 a , b ∈ A a,b\in A a,b∈A则aRb当且仅当 R ( a ) = R ( b ) R(a)=R(b) R(a)=R(b)
三、函数与映射
1.单射,满射与双射
1.定义
- 设映射 f : A → B f:A\rightarrow B f:A→B,如果 R a n ( f ) = B Ran(f)=B Ran(f)=B,那么就是满射,也就是说 ∀ y ∈ B , 都 存 在 x ∈ A , 使 得 f ( x ) = y \forall y \in B,都存在x\in A,使得f(x)=y ∀y∈B,都存在x∈A,使得f(x)=y(y中所有的值都能被映射到)
- 设映射 f : A → B f:A\rightarrow B f:A→B,如果任意的 y ∈ R a n ( f ) y\in Ran(f) y∈Ran(f)都存在唯一的 x ∈ A x \in A x∈A使得 f ( x ) = y f(x)=y f(x)=y,则称单射,也就是说对于任意的 a , b ∈ A a,b \in A a,b∈A,如果a≠b,都有 f ( a ) ≠ f ( b ) f(a)≠f(b) f(a)=f(b)(函数值y与x一一对应,没有重复的)
- 如果f既是单射,又是满射,则称f是双射
2.与关系矩阵和关系图的关系
- 如果一个A到B的函数是单射,那么关系矩阵中每一列只会有一个1,如果它是满射,则每一列至少有一个1,如果是双射,每一行与每一列都恰好有一个1
- 对于关系图而言,如果A到B是单射,那么关系图每个顶点至多存在一条指向它的边(入度不超过1),如果A到B是满射,那么关系图每一个顶点至少存在一条指向它的边(入度不少于1),如果是双射,关系图中每个顶点都发出一条有向边,且恰好存在一条指向它的边
3.函数的复合
- 复合具有传递性,如果两个函数都是同一种射的话,复合之后也是同一个射
- 如果 g ∘ f g\circ f g∘f是单射,那么 f f f是单射
- 如果 g ∘ f g\circ f g∘f是满射,那么 g g g是满射
- 如果 g ∘ f g\circ f g∘f是双射,那么 f f f是单射, g g g是满射
4.几种常见函数
- 特征函数
设U为全集,对于任何集合 A ⊆ U A\subseteq U A⊆U,其特征函数定义为:
χ A ( a ) = { 1 , a ∈ A 0 , a ∉ A \chi_A(a)= \begin{cases} 1,a\in A \\ 0,a \notin A \\ \end{cases} χA(a)={1,a∈A0,a∈/A - 置换函数
假设非空优先集合S包含n个元素,S上的一个双射称为S的一个n元置换,其中n是置换的阶,表示为
π = ( x 1 x 2 . . . x n f ( x 1 ) f ( x 2 ) . . . f ( x n ) ) \pi= \begin{pmatrix} x_1&x_2&...&x_n\\ f(x_1)&f(x_2)&...&f(x_n)\\ \end{pmatrix} π=(x1f(x1)x2f(x2)......xnf(xn))
其中S的任意一个置换都有n!种表示
假设 π \pi π是集合S的一个置换,那么其周期一定存在,也就是说经过若干次置换后又会回到原来的顺序
假设有限集合S包含n个元素,以 ( a 1 , a 2 . . . a r ) (a_1,a_2...a_r) (a1,a2...ar)表示一个轮换,它的意思是,除了这r个映射映射到不同位置上,其他的映射都映射到自身,这个称为一个r-轮换
任一置换可以表示成任意不相交轮换的积 - 哈希函数(散列函数/杂凑函数)
作用:将任意长度的输入打乱,混合,压缩映射成一个定长的输出,可将数据量变少,然后将数据格式固定下来
定义:设A为有限集合,n为一个确定正整数,如果存在一个映射H,使得无限集合H: A ∗ → A n A^* \rightarrow A^n A∗→An,则称为哈希函数
造成问题:很明显,无限集合映射到有限集合并不是单射,所以一定存在多对一的情况,那么在工业互联网中的通信问题就会产生冲突碰撞,所以好的哈希函数应该减少碰撞的产生,并且散列值应该均匀的分布在整个值域范围内,实现负载均衡,就可以减少冲突的出现
5.函数的势
定义:如果A,B是两个集合,如果存在A到B的双射,那么我们说这两个集合是等势的,并且基数相等,记作|A|=|B|,等势关系也是一种等价关系
推论:
- 有限集合的真子集不与其等势,无限集合必与其某个真子集等势
- 不等势的集合是存在单射的前提下不满足双射,比如自然数集就与实数集不等势
四、偏序关系
1.定义
假设R是集合A上的关系,如果R是自反的,反对称的和传递的,则称R是A上的一个偏序关系,一般记作≤或者≥
所以任何的恒等关系,整除关系,包含关系,大于等于关系都是A上的偏序关系
2.性质
- 偏序关系具有保号性,也就说A是偏序集,如果 B ⊆ A B\subseteq A B⊆A,那么B也是偏序集
- 如果R是A上的偏序关系, R − 1 R^{-1} R−1也是A上的偏序关系,那么我们称之为R的对偶
- 如果(A,R)是偏序集, a , b ∈ A a,b\in A a,b∈A,如果 a ≤ b 或 b ≤ a a \leq b或b\leq a a≤b或b≤a成立,那么我们称a,b是可比的,如果对于任意的 a , b ∈ A a,b\in A a,b∈A都是可比的,那么我们称R为线序或全序,(A,R)是线序集或全序集,也称为链
- 如果集合是非自反的,但是满足传递关系,那么R一定是非对称的,R是A上的拟序关系
- 如果R是一个拟序关系,那么 r ( R ) = R ⋃ I A r(R)=R\bigcup I_A r(R)=R⋃IA是一个偏序关系,反之差集亦然
- 如果(A,≤)和(A’,≤’)是两个偏序集,如果函数 f : A → A ′ f:A\rightarrow A' f:A→A′是双射关系,如果当任意 a ≤ b a\leq b a≤b当且仅当 f ( a ) ≤ ′ f ( b ) f(a)\leq' f(b) f(a)≤′f(b),则称两者是一个同构关系,并且两个映射的逆也是同构
3.积偏序与字典序
假设 ( A , ≤ 1 ) 和 ( B , ≤ 2 ) (A,≤_1)和(B,≤_2) (A,≤1)和(B,≤2)都是偏序集,那么我们定义其笛卡尔乘积的偏序关系≤为 ( a , b ) ≤ ( a ′ , b ′ ) (a,b)\leq (a',b') (a,b)≤(a′,b′)当且仅当 a ≤ 1 a ′ , b ≤ 2 b ′ a\leq_1a',b\leq_2 b' a≤1a′,b≤2b′为积偏序,记作 ( A × B , ≤ ) = ( A , ≤ 1 ) × ( B , ≤ 2 ) (A×B,≤)=(A,≤_1)×(B,≤_2) (A×B,≤)=(A,≤1)×(B,≤2)
假设 ( A , ≤ 1 ) 和 ( B , ≤ 2 ) (A,≤_1)和(B,≤_2) (A,≤1)和(B,≤2)都是偏序集,那么我们定义其笛卡尔乘积的偏序关系≤为 ( a , b ) ≤ ( a ′ , b ′ ) (a,b)\leq (a',b') (a,b)≤(a′,b′)当且仅当 a ≤ 1 a ′ a\leq_1a' a≤1a′或 a = a ′ , b ≤ 2 b ′ a=a',b\leq_2 b' a=a′,b≤2b′为词偏序或字典序
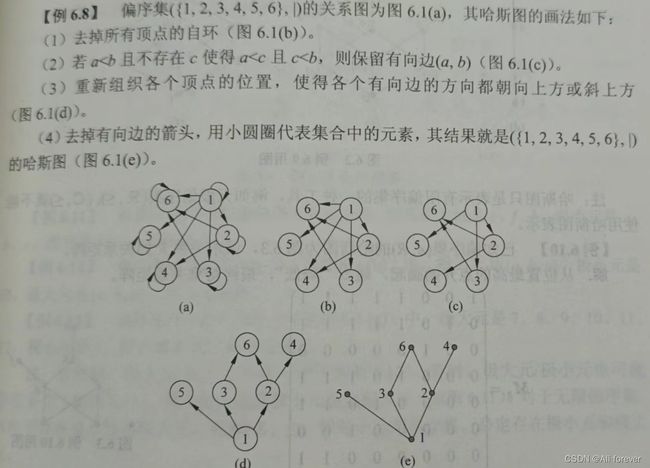
4.哈斯图
作用:哈斯图是用来表示有限偏序集的一种数学图表,它是一种图形形式的对偏序集的传递简约。
定理:假设 ( A , ≤ ) (A,≤) (A,≤)是偏序集,则在拟序集图中不存在道路长度超过1的节点(无闭环)
步骤:
- 去掉所有顶点的自环,得到拟序关系<的关系图
- 若a<b且不存在c使得a<c且c<b,那么保留有向边(a,b)
- 重新组织每个顶点的位置,使得每个有向边的方向都朝向上方或者斜上方
- 去掉边的箭头,用小圆圈代表集合中的元素
5.偏序集中的特殊元素
- 极大元与极小元:在偏序集里面只要存在 x ∈ A x\in A x∈A,并且不存在 a ∈ A a\in A a∈A使得 x < a ( a < x ) x<a(a<x) x<a(a<x),那么我们就称x是极大元(极小元)
极大元和极小元可能有多个,因为在这个偏序集里面不需要满足全可比,只需满足部分可比性就好了 - 最大元与最小元: 在偏序集里面存在 x ∈ A x\in A x∈A,对所有的 a ∈ A a\in A a∈A,使得 a ≤ x ( x ≤ a ) a\leq x(x\leq a) a≤x(x≤a),那么我们就称x是最大元(最小元)
最大元和最小元可能不存在,因为最大元与最小元的存在条件是整个偏序集是完全可比的,否则会出现无法比较的情形,所以最大元最小元最多只能有一个 - 假设元素x是集合B的上界(大元),如果对所有上界a都有 x ≤ a x\leq a x≤a,那么我们称这个为上确界,也叫最小上界,记作LUB(B)
- 假设元素x是集合B的下界(小元),如果对所有下界a都有 a ≤ x a\leq x a≤x,那么我们称这个为下确界,也叫最大下界,记作GLB(B)

上界与下界都需要对相应的元素是完全可比的,如果不可比则不存在
总结
本文主要介绍了集合论的重点内容作为后面研究的重点图论的基础知识,本文是综合清华大学离散数学书籍以及哈工大慕课视频进行的归纳总结,下一步将会介绍图论这一重要应用