搞机器学习不会线性代数？那怎么行

搞机器学习不会线性代数？那怎么行！

线性代数主要研究线性空间中对象的运动规律。

两个关键问题：

• 线性空间中的对象
• 线性空间中对象的运动规律

哈哈，有点废话文学

线性空间中的对象称为向量，通常是选定一组线性无关的基向量，通过基向量的线性组合来表示。

而线性空间中的运动被称为线性变换，描述了线性空间中的对象也就是向量是如何运动的。这种线性变换是通过矩阵的形式来描述的。

线性空间中使得某个对象（向量）发生某种运动（线性变换）的方法，就是用描述对应运动的矩阵去乘以表示对应对象的向量。

简单的说， 确定了线性空间中的一组线性无关的基向量后，线性空间中的任一对象都可以用向量来刻画，对象的运动则由矩阵乘以向量来表达。

而这个矩阵自身又可以看作线性空间基向量被施加了同一线性变换。【是不是感觉又统一起来 了】

1 直观真正理解向量

其实在初中阶段我们就接触过“向量”这个概念，知道向量具有方向和大小，大学阶段“向量”又变成了线性代数的基础概念。

一个典型的二维空间里的向量如下图所示：

向量在形式上表现为一系列有序数组，可以看作空间中具有方向和大小的一个箭头，而实际上向量可以表示任何符合向量规则的事物。

这里我们说一个问题，为什么以前的书上会标注这样一句话：“一般没有指明，默认向量为列向量”。

【原因】

虽然向量既可以写成行向量（一行数组），也可以写成列向量（一列数组），之所以会这样子说，这是因为矩阵乘积的习惯性写法是“先对象后操作”，即

$$Ax$$

所以要求向量x放置在矩阵A的右边。

由于矩阵A (m x n) 一般具有n列，根据矩阵乘法的规则要求，向量x (n x 1) 需要具有n 行，这样就清楚了，即要求向量 x 是列向量。

因此！为了符合矩阵乘法的标记习惯，我们一般所指的向量默认为列向量。

2 理解向量的加法与数乘

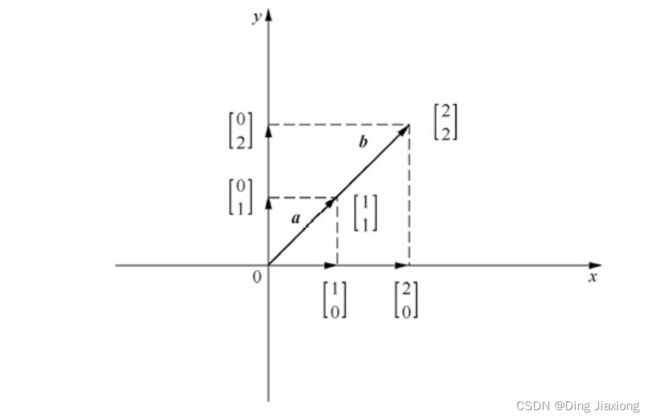
从物理视角来看，一个向量可以看作从原点出发沿着向量方向行走向量大小的距离所到达的位置，如果在此位置继续沿着某个向量行走，结果就应该是两个向量之和的位置。

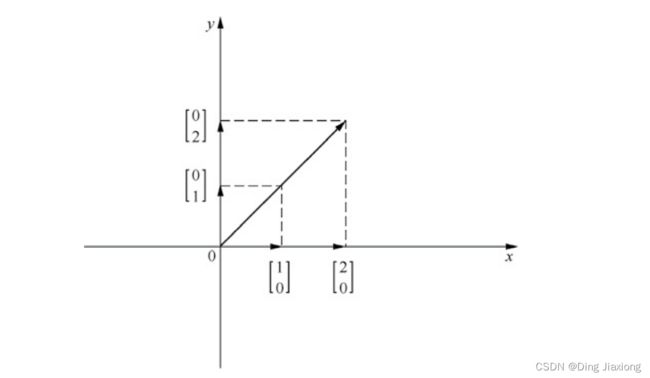
例如一个向量 $\left[\begin{array}{l}2\\ 2\end{array}\right]$ 从物理视角可以看作，从原点 $\left[\begin{array}{l}0\\ 0\end{array}\right]$ 出发，首先沿着x轴正方向行走2个单位长度，然后沿着y轴正方向行走2个单位长度。

上面过程的实质就是，将x轴的单位向量i沿着x轴正方向伸长2倍得到向量2i，即 $\left[\begin{array}{l}2\\ 0\end{array}\right]$ ，将y轴单位向量j沿着y轴正方向伸长2倍得到向量2j，即 $\left[\begin{array}{l}0\\ 2\end{array}\right]$ ，将这两个向量相加得到我们所求的向量

$$\left[\begin{array}{l}2\\ 0\end{array}\right]+\left[\begin{array}{l}0\\ 2\end{array}\right]=\left[\begin{array}{l}2\\ 0\end{array}\right]$$

这就是向量加法的实现过程。

向量加法中有一种特殊的情况，那就是向量数乘。λv表示λ个v向量相加，也就是将v向量拉伸（压缩）λ倍。

例如，3v表示将v向量沿着原来的向量方向拉伸3倍，-0.5v表示沿着v向量的反方向将其压缩为原来的1/2。

一般教科书中是这样描述向量数乘规则的：向量进行数乘运算时将标量与向量的每个元素分别相乘即可得到结果向量。

向量加法与数乘虽然简单，却是线性空间的基础，因为向量通过加法和数乘构成向量的线性组合。

3 理解向量乘法的本质

向量乘法分为向量内积和向量外积两种形式。

3.1 向量内积

向量内积也称向量点积或者数量积，有两种定义方式：代数方式和几何方式。

【1】向量内积的的代数定义

两个向量内积的运算规则是，参与向量内积的两个向量必须维度相等，向量内积运算时将两个向量对应位置上的元素分别相乘之后求和即可得到向量内积的结果。

向量内积的结果是一个标量。

例如：

设有两个维度相同的向量 a = [ a 1 a 2 a 3 ⋮ a n ] \boldsymbol{a}=\left[\begin{array}{c}a_1 \\ a_2 \\ a_3 \\ \vdots \\ a_n\end{array}\right] a= ​a1​a2​a3​⋮an​​ ​ 和 b = [ b 1 b 2 b 3 ⋮ b n ] ​ \boldsymbol{b}=\left[\begin{array}{c}b_1 \\ b_2 \\ b_3 \\ \vdots \\ b_n\end{array}\right]​ b= ​b1​b2​b3​⋮bn​​ ​​

那么这两个向量内积为
a ⋅ b = [ a 1 a 2 a 3 ⋮ a n ] ⋅ [ b 1 b 2 b 3 ⋮ b n ] = a 1 b 1 + a 2 b 2 + a 3 b 3 + ⋯ + a n b n \boldsymbol{a} \cdot \boldsymbol{b}=\left[\begin{array}{c} a_1 \\ a_2 \\ a_3 \\ \vdots \\ a_n \end{array}\right] \cdot\left[\begin{array}{c} b_1 \\ b_2 \\ b_3 \\ \vdots \\ b_n \end{array}\right]=a_1 b_1+a_2 b_2+a_3 b_3+\cdots+a_n b_n a⋅b= ​a1​a2​a3​⋮an​​ ​⋅ ​b1​b2​b3​⋮bn​​ ​=a1​b1​+a2​b2​+a3​b3​+⋯+an​bn​

【2】向量内积的几何定义

向量内积的几何定义用来表征向量a在向量b方向上的投影长度乘以向量b的模长，即

$$\mathbf{a}\cdot \mathbf{b}=|\mathbf{a}||\mathbf{b}|\cos \theta$$

如果向量b是单位向量（即模长为1），那么向量a与向量b的内积结果就等于向量a在向量b方向上的投影长度。

这就是向量内积的几何定义。

3.2 向量外积

向量外积又叫向量积、叉积，也是线性代数中一种常见的向量运算。

向量外积也可以从代数和几何两个角度来理解，两个向量外积的运算规则较为复杂，我们只考虑二维空间和三维空间中的情况。

【1】二维空间中向量外积

从代数角度考虑，二维空间中向量a和向量b的外积运算法则为
$$\mathbf{a}\times \mathbf{b}=\left[\begin{array}{l}{a}_1\\ a_2\end{array}\right]\times \left[\begin{array}{l}{b}_1\\ b_2\end{array}\right]=a_1{b}_2-a_2{b}_1$$

这种情况下，向量外积的结果是一个标量。

从几何角度考虑，二维空间中向量a和向量b外积的结果可以表达为
$$\mathbf{a}\cdot \mathbf{b}=|\mathbf{a}||\mathbf{b}|\sin \theta$$

它表示向量a和向量b张成的平行四边形的“面积”。如果向量a和向量b的夹角大于180度，那么向量外积的结果为负数。

例如，通过代码来求解向量a和向量b外积，可以发现外积与向量夹角度数有关。

二维空间中向量外积的计算结果如下：

import numpy as np

a = np.array([1, 2])
b = np.array([3, 4])

print(np.cross(a, b))
print("*" * 100)
print(np.cross(b, a))

【2】三维空间的向量外积

从代数角度考虑，三维空间中向量a和向量b的外积运算法则为
a × b = [ a 1 a 2 a 3 ] × [ b 1 b 2 b 3 ] = [ a 2 b 3 − a 3 b 2 a 3 b 1 − a 1 b 3 a 1 b 2 − a 2 b 1 ] \boldsymbol{a} \times \boldsymbol{b}=\left[\begin{array}{l} a_1 \\ a_2 \\ a_3 \end{array}\right] \times\left[\begin{array}{l} b_1 \\ b_2 \\ b_3 \end{array}\right]=\left[\begin{array}{c} a_2 b_3-a_3 b_2 \\ a_3 b_1-a_1 b_3 \\ a_1 b_2-a_2 b_1 \end{array}\right] a×b= ​a1​a2​a3​​ ​× ​b1​b2​b3​​ ​= ​a2​b3​−a3​b2​a3​b1​−a1​b3​a1​b2​−a2​b1​​ ​

这种情况下，向量外积的结果是一个向量。

从几何角度考虑，三维空间中向量a和向量b外积的结果是向量a和向量b张成平面的法向量。三维空间中，向量外积的结果是一个向量，而不是一个标量，并且两个向量的外积与这两个向量组成的坐标平面垂直。

例如，通过代码来求解三维空间中向量a和向量b外积，可以发现向量外积顺序不同会导致法向量方向不同。

三维空间中向量外积的计算结果如图下

# 三维空间
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])

print(np.cross(a, b))
print("*" * 100)
print(np.cross(b, a))

计算结果

4 理解基向量与线性无关

4.1 如何理解基向量

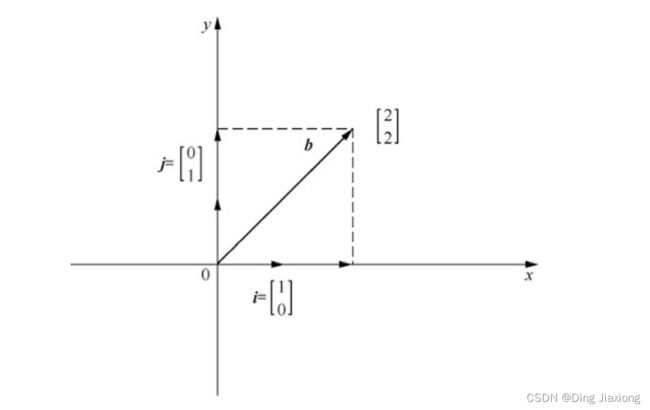
二维空间上一个向量 $a=\left[\begin{array}{l}1\\ 2\end{array}\right]$ 通常被理解为，一条在x轴上投影为1、y轴上投影为2的有向线段。

这种理解方式其实隐含着一个假设，即

$a=\left[\begin{array}{l}1\\ 2\end{array}\right]$ 是以 x轴和 y轴为正方向且 以长度为 1 的向量 $\left[\begin{array}{l}1\\ 0\end{array}\right]$ 和向量 $\left[\begin{array}{l}0\\ 1\end{array}\right]$ 为基准的一种表达方式。

一般来说，平面直角坐标系中以向量 $\left[\begin{array}{l}1\\ 0\end{array}\right]$ 和向量 $\left[\begin{array}{l}0 \ 1\end{array}\right] $ 作为基向量，

该坐标系内的任一向量 $\left[\begin{array}{l}x\\ y\end{array}\right]$ 都可以由基向量 $\left[\begin{array}{l}1\\ 0\end{array}\right]$ 和基向量 $\left[\begin{array}{l}0\\ 1\end{array}\right]$ 的线性组合 $x\left[\begin{array}{l}1\\ 0\end{array}\right]+y\left[\begin{array}{l}0\\ 1\end{array}\right]$ 得到

也就是说，某个向量的坐标表示与空间中基向量的选取密切相关，不同基向量下的坐标表示是不同的。

4.2 如何理解线性无关

看个问题，如果是在二维空间中，是否任意两个向量都可以作为基向量来表示空间中的任何向量呢？

先给出答案，是否定的。【并非任意两个向量都可以】

向量b与a共线的充要条件是：存在唯一实数λ，使得b=λa

例如：

二维空间中向量 $\left[\begin{array}{l}1\\ 0\end{array}\right]$ 和向量 $\left[\begin{array}{l}-1\\ 0\end{array}\right]$ 是共线向量。

向量 $ a= \left[\begin{array}{l}1 \ 2\end{array}\right]$ 就无法写成上面两个向量的某个线性组合形式。

因此 向量 $\left[\begin{array}{l}1\\ 0\end{array}\right]$ 和向量 $\left[\begin{array}{l}-1\\ 0\end{array}\right]$ 就无法作为一组基向量。

实际上n维空间中的基向量必须满足n维空间具有n个基向量，且这些基向量之间必须线性无关。

【所以什么是线性无关？】

例如向量 ${\mathbf{V}}_1,{\mathbf{V}}_2,{\mathbf{V}}_3,\cdots ,{\mathbf{V}}_m$ ，线性无关 实际上指的是这其中任何一个 向量 ${\mathbf{V}}_i$ 不能由其他向量的线性组合得到

用公式表示就是 $K_1{V}_1+K_2{V}_2+\cdots +K_m{V}_m=0$ 当且仅当 $K_1=K_2=\cdots K_m=0$ 时成立。

通俗的解释就是，由一组向量的线性组合得到零向量只能通过所有系数为0这种方式实现，那么这组向量就是线性无关的，反之则是线性相关的。【熟悉的知识有没有突然攻击你】

一组向量线性相关就是指这些向量中至少有一个向量对于生成最高维度的向量空间是“没有贡献”的（因为它可以由别的向量的线性组合得到）。

反过来讲，如果所有的向量都无法通过其他向量线性组合的方式得到，每个向量都给张成的新空间做出了“贡献”，也就是**“一个都不能少”**，那么就说这些向量是线性无关的。

5 真正理解矩阵

5.1 矩阵运算规则

矩阵是整个线性代数的核心和关键，它能够实现向量在空间中的映射变换。

【1】如何理解矩阵

以前我们 在书中看见的矩阵定义一般是：由 $m\times n$ 个数 $a_{ij}$ 排成的 m 行 n 列的数表，我们把它称为 m 行 n 列的矩阵，简称 $m\times n$ 矩阵，记作：

A = [ a 11 a 12 a 13 ⋯ a 1 n a 21 a 22 a 23 ⋯ a 2 n a 31 a 32 a 33 ⋯ a 3 n ⋮ ⋮ ⋮ ⋮ a m 1 a m 2 a m 3 ⋯ a m n ] \boldsymbol{A}=\left[\begin{array}{ccccc} a_{11} & a_{12} & a_{13} & \cdots & a_{1 n} \\ a_{21} & a_{22} & a_{23} & \cdots & a_{2 n} \\ a_{31} & a_{32} & a_{33} & \cdots & a_{3 n} \\ \vdots & \vdots & \vdots & & \vdots \\ a_{m 1} & a_{m 2} & a_{m 3} & \cdots & a_{m n} \end{array}\right] A= ​a11​a21​a31​⋮am1​​a12​a22​a32​⋮am2​​a13​a23​a33​⋮am3​​⋯⋯⋯⋯​a1n​a2n​a3n​⋮amn​​ ​

其实我们前面说的向量，它就是一种最简单的 矩阵。

例如n维行向量可以看作一个1×n的特殊矩阵，而n维列向量可以看作一个n×1的特殊矩阵。

一些特殊的矩阵：

① 方阵：方阵是行数和列数相等的矩阵，方阵的行数或列数称为阶数。
A = [ 1 2 3 4 5 6 7 8 9 ] \boldsymbol{A}=\left[\begin{array}{lll} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{array}\right] A= ​147​258​369​ ​

例如上面这个就是一个三阶方阵。

② 对角矩阵：对角矩阵是非主对角线元素全部为0的方阵。

主对角线：从左上到右下

例如矩阵 A = [ 1 0 0 0 5 0 0 0 9 ] ​ \boldsymbol{A}=\left[\begin{array}{lll} 1 & 0 & 0 \\ 0 & 5 & 0 \\ 0 & 0 & 9 \end{array}\right]​ A= ​100​050​009​ ​​ 这就是一个对角矩阵。记得：对角矩阵必然是方阵。

③ 单位矩阵：单位矩阵是主对角线元素为1的对角矩阵。

例如矩阵 A = [ 1 0 0 0 1 0 0 0 1 ] \boldsymbol{A}=\left[\begin{array}{lll} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right] A= ​100​010​001​ ​ 这就是个单位矩阵。记得：单位矩阵必然是对角矩阵，也必然是方阵。

④ 对称矩阵。对称矩阵是原始矩阵和它的转置矩阵相等的矩阵。

一个矩阵的转置矩阵是将该矩阵行和列上的元素进行位置互换之后的矩阵。

例如矩阵 A = [ 1 2 3 4 5 6 ] \boldsymbol{A}=\left[\begin{array}{lll} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{array}\right] A= ​135​246​ ​ 的转置矩阵为 $A^{\mathrm{T}}=\left[\begin{array}{lll}1& 3& 5\\ 2& 4& 6\end{array}\right]$ 。原始矩阵和它的转置矩阵相等，所以

A = [ 1 0 0 0 5 0 0 0 9 ] \boldsymbol{A}=\left[\begin{array}{lll} 1 & 0 & 0 \\ 0 & 5 & 0 \\ 0 & 0 & 9 \end{array}\right] A= ​100​050​009​ ​ 是一个对称矩阵。记得：对称矩阵必然是方阵。

【2】理解矩阵加法和数乘

矩阵加法【减法就是逆运算】只适用于规模相等的矩阵之间，也就是说只有矩阵之间的行数和列数分别相等才能够进行加法运算。

例如：
[ 1 2 3 4 5 6 ] + [ 2 3 4 1 5 2 ] = [ 1 + 2 2 + 3 3 + 4 4 + 1 5 + 5 6 + 2 ] = [ 3 5 7 5 10 8 ] \left[\begin{array}{ll} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{array}\right]+\left[\begin{array}{ll} 2 & 3 \\ 4 & 1 \\ 5 & 2 \end{array}\right]=\left[\begin{array}{ll} 1+2 & 2+3 \\ 3+4 & 4+1 \\ 5+5 & 6+2 \end{array}\right]=\left[\begin{array}{ll} 3 & 5 \\ 7 & 5 \\ 10 & 8 \end{array}\right] ​135​246​ ​+ ​245​312​ ​= ​1+23+45+5​2+34+16+2​ ​= ​3710​558​ ​

矩阵数乘是一类特殊的矩阵加法，它的结果就是将参与运算的标量数字分别与矩阵的各元素相乘，得到的结果作为新矩阵的各元素，例如：
$$2\left[\begin{array}{ccc}1& 4& 3\\ 4& -2& 2\end{array}\right]=\left[\begin{array}{lll}2\times 1& 2\times 4& 2\times 3\\ 2\times 4& 2\times (-2)& 2\times 2\end{array}\right]=\left[\begin{array}{ccc}2& 8& 6\\ 8& -4& 4\end{array}\right]$$

【3】理解矩阵乘法

矩阵乘法也只适用于具备某些条件的矩阵之间，两个矩阵相乘仅当第一个矩阵A的列数和另一个矩阵B的行数相等时才能定义。

例如A 是 $m\times n$ 矩阵和 B 是 $n\times p$ 矩阵，它们的乘积 C 是一个 $m\times p$ 矩阵，并将此乘积记为 $C=AB$

举个栗子：
[ 1 0 2 − 1 3 1 ] × [ 3 1 2 1 1 0 ] = [ ( 1 × 3 + 0 × 2 + 2 × 1 ) ( 1 × 1 + 0 × 1 + 2 × 0 ) ( − 1 × 3 + 3 × 2 + 1 × 1 ) ( − 1 × 1 + 3 × 1 + 1 × 0 ) ] = [ 5 1 4 2 ] \left[\begin{array}{lll} 1 & 0 & 2 \\ -1 & 3 & 1 \end{array}\right] \times\left[\begin{array}{ll} 3 & 1 \\ 2 & 1 \\ 1 & 0 \end{array}\right]=\left[\begin{array}{ll} (1 \times 3+0 \times 2+2 \times 1) & (1 \times 1+0 \times 1+2 \times 0) \\ (-1 \times 3+3 \times 2+1 \times 1) & (-1 \times 1+3 \times 1+1 \times 0) \end{array}\right]=\left[\begin{array}{cc} 5 & 1 \\ 4 & 2 \end{array}\right] [1−1​03​21​]× ​321​110​ ​=[(1×3+0×2+2×1)(−1×3+3×2+1×1)​(1×1+0×1+2×0)(−1×1+3×1+1×0)​]=[54​12​]

其实我们可以发现一些规律：

• 左边矩阵的列数必须和右边矩阵的行数相等才可以运算。
• 左边矩阵的行数和右边矩阵的列数决定了结果矩阵的行列数值。
• 结果矩阵中每个元素的数值等于左边矩阵对应行元素与右边矩阵对应列元素分别相乘再求和的结果。

5.2 矩阵和向量之间乘法的本质

矩阵乘以向量常写作Ax形式，其中左边是矩阵A，右边是列向量x。

矩阵向量乘法可以看作矩阵乘以矩阵的一种特例，特殊之处在于列向量可以看作列数为1的特殊矩阵。

例如矩阵 A = [ 1 2 3 4 5 6 ] \boldsymbol{A}=\left[\begin{array}{ll}1 & 2 \\ 3 & 4 \\ 5 & 6\end{array}\right] A= ​135​246​ ​ 和向量 $\mathbf{x}=\left[\begin{array}{l}1\\ 1\end{array}\right]$ 相乘的结果为 A x = [ 1 2 3 4 5 6 ] × [ 1 1 ] = [ 3 7 11 ] \boldsymbol{A x}=\left[\begin{array}{ll}1 & 2 \\ 3 & 4 \\ 5 & 6\end{array}\right] \times\left[\begin{array}{l}1 \\ 1\end{array}\right]=\left[\begin{array}{l}3 \\ 7 \\ 11\end{array}\right] Ax= ​135​246​ ​×[11​]= ​3711​ ​

即假设 二维空间中的一个坐标点(1,1)经过矩阵A作用后映射成了三维空间中的另一个坐标点(3,7,11)。

这个例子说明什么呢？

原始空间中的列向量x不仅发生了位置变化，连列向量x所在的空间也发生了改变。

从运动的视角来看，矩阵向量乘法可以理解为对线性空间中运动（线性变换）的一种描述。对于任意线性空间，只要选定一组线性无关的基向量就可以使用矩阵的形式来描述空间中的任意一个线性变换。

【1】什么是线性变换

变换本质上就是函数，函数的特点是接收输入内容并输出对应的结果，线性变换本质上也是一种函数。

线性变换这种函数的特别之处在于：接收的是向量，输出的也是向量。

之所以使用“线性变换”而不是“函数”来称呼这种关系，主要是为了强调这种函数关系的特点是“输入向量通过某种线性变换成为输出向量”。

所以 什么样的变换是线性变换？

假设线性空间V中有一种变换L，使得对于线性空间V中任意两个元素x和y，以及任意实数a和b，

总是有$L(ax+by)=aL(x)+bL(y)$ ，就称L为线性变换。

直观来讲，就是把空间想象成沿着各个坐标轴刻度画出网格线的空间，如果变换前后原点固定且网格线保持平行和等距分布，那么这种变换就是线性变换。

例如矩阵 $\left[\begin{array}{ll}0& -1\\ 1& 0\end{array}\right]$ 所描述的变换表示在空间中围绕原点逆时针旋转90度的变换，变换前后原点固定且网格线仍然保持平行和等距分布，因此这就是一种线性变换

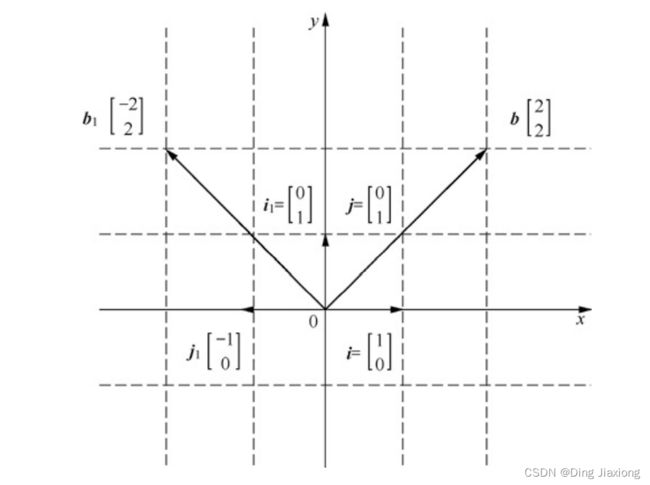
举个栗子：

上面的图中，向量b的原始基向量为i和j，向量$b=2i+2j$ 经过矩阵 $\left[\begin{array}{ll}0& -1\\ 1& 0\end{array}\right]$ 的线性变换后，映射为新的向量b1，且基向量变为i1和j1。有$b_1=2i_1+2j_1$

$$\left[\begin{array}{ll}0& -1\\ 1& 0\end{array}\right]\left[\begin{array}{l}2\\ 2\end{array}\right]=2\left[\begin{array}{l}0\\ 1\end{array}\right]+2\left[\begin{array}{l}-1\\ 0\end{array}\right]=\left[\begin{array}{l}-2\\ 2\end{array}\right]$$

牛逼

【2】矩阵向量乘法描述了线性变换

矩阵向量乘法描述的是线性空间中的一种线性变换，原始向量在矩阵所对应的线性变换作用下空间位置甚至空间维度和形态都发生了改变，这就是矩阵的空间映射作用。

从数值表示来看，矩阵A与列向量x的乘积Ax就等于将原始列向量x的默认基向量分别对应地变换为矩阵A
的各列，由矩阵A的各列作为目标向量的新基向量。

一个直观的方法就是关注并跟踪线性空间基向量的去向。

举个栗子：二维空间里面的任何一个向量 $\left[\begin{array}{l}x\\ y\end{array}\right]$ 都可以看作 $x\left[\begin{array}{l}1\\ 0\end{array}\right]+y\left[\begin{array}{l}0\\ 1\end{array}\right]$

根据线性变换的定义，我们可以得到线性变换之后的新向量$L\left(\left[\begin{array}{l}x\\ y\end{array}\right]\right)=xL\left(\left[\begin{array}{l}1\\ 0\end{array}\right]\right)+yL\left(\left[\begin{array}{l}0\\ 1\end{array}\right]\right)$

所以矩阵的数值描述了该线性变换导致原始线性空间中基向量变换后的形态。

假如某个线性变换使得原始基向量 $\left[\begin{array}{l}1 \ 0\end{array}\right] $和 $ \left[\begin{array}{l}0 \ 1\end{array}\right]$ 变换为新的基向量 $\left[\begin{array}{l}a \ c\end{array}\right] $和 $ \left[\begin{array}{l}b \ d\end{array}\right]​$

那么原来的任一向量 $\left[\begin{array}{l}x\\ y\end{array}\right]$ 都会变换为目标向量 $x\left[\begin{array}{l}a\\ c\end{array}\right]+y\left[\begin{array}{l}b\\ d\end{array}\right]$ 【没毛病】

如果将变换后基向量 $\left[\begin{array}{l}a \ c\end{array}\right] $和 $ \left[\begin{array}{l}b \ d\end{array}\right]$ 的坐标放在一个2×2的格子里，得到一个2×2的矩阵 $\left[\begin{array}{ll}a& b\\ c& d\end{array}\right]$

这个矩阵就描述了这个线性变换，其中矩阵的每一列就表示线性变换之后的基向量的去向。

实际上从上面的过程我们很容易理解矩阵向量乘法的规则，如
$$\left[\begin{array}{ll}a& b\\ c& d\end{array}\right]\left[\begin{array}{l}x\\ y\end{array}\right]=x\left[\begin{array}{l}a\\ c\end{array}\right]+y\left[\begin{array}{l}b\\ d\end{array}\right]=\left[\begin{array}{l}ax+by\\ cx+dy\end{array}\right]$$

就显得很自然和符合道理了。【牛逼牛逼】

【3】矩阵向量乘法实现空间映射

矩阵描述的是空间中的一种线性变换，矩阵向量乘法就是将这种线性变换施加于空间中的某个向量，这会使得向量位置甚至其所在空间的维度和形态都发生改变。

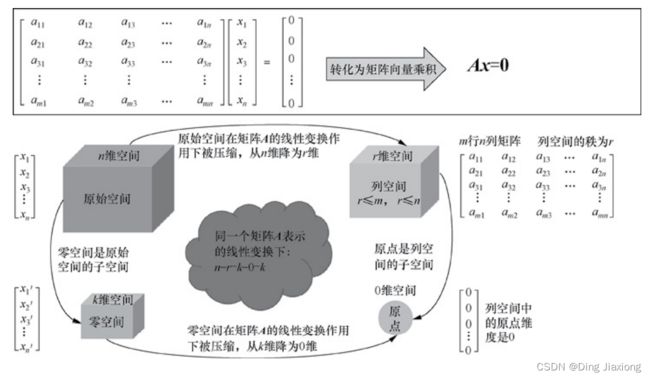
一般来说，矩阵A具有m行和n列，向量x是一个n维列向量，那么矩阵A与向量x的乘法Ax的结果就是，将原始基向量变换为矩阵A的各列，用矩阵A的各列作为新的基向量，向量x的各元素分别作为对应的系数，最终可以得到Ax的结果，如下所示。

[ a 11 a 12 a 13 ⋯ a 1 n a 21 a 22 a 23 ⋯ a 2 n a 31 a 32 a 33 ⋯ a 3 n ⋮ ⋮ ⋮ ⋮ a m 1 a m 2 a m 3 ⋯ a m n ] [ x 1 x 2 x 3 ⋮ x n ] = x 1 [ a 11 a 21 a 31 ⋮ a m 1 ] + x 2 [ a 12 a 22 a 32 ⋮ a m 2 ] + ⋯ + x n [ a 1 n a 2 n a 3 n ⋮ a m n ] \left[\begin{array}{ccccc} a_{11} & a_{12} & a_{13} & \cdots & a_{1 n} \\ a_{21} & a_{22} & a_{23} & \cdots & a_{2 n} \\ a_{31} & a_{32} & a_{33} & \cdots & a_{3 n} \\ \vdots & \vdots & \vdots & & \vdots \\ a_{m 1} & a_{m 2} & a_{m 3} & \cdots & a_{m n} \end{array}\right]\left[\begin{array}{c} x_1 \\ x_2 \\ x_3 \\ \vdots \\ x_n \end{array}\right]=x_1\left[\begin{array}{c} a_{11} \\ a_{21} \\ a_{31} \\ \vdots \\ a_{m 1} \end{array}\right]+x_2\left[\begin{array}{c} a_{12} \\ a_{22} \\ a_{32} \\ \vdots \\ a_{m 2} \end{array}\right]+\cdots+x_n\left[\begin{array}{c} a_{1 n} \\ a_{2 n} \\ a_{3 n} \\ \vdots \\ a_{m n} \end{array}\right] ​a11​a21​a31​⋮am1​​a12​a22​a32​⋮am2​​a13​a23​a33​⋮am3​​⋯⋯⋯⋯​a1n​a2n​a3n​⋮amn​​ ​ ​x1​x2​x3​⋮xn​​ ​=x1​ ​a11​a21​a31​⋮am1​​ ​+x2​ ​a12​a22​a32​⋮am2​​ ​+⋯+xn​ ​a1n​a2n​a3n​⋮amn​​ ​

一个原始空间经过矩阵A的线性变换作用后得到的对应空间就是矩阵A各列线性组合的集合，这个集合被称为矩阵A的列空间C(A)。

例如，一个3×2矩阵 A = [ 1 1 0 4 0 5 ] \boldsymbol{A}=\left[\begin{array}{ll}1 & 1 \\ 0 & 4 \\ 0 & 5\end{array}\right] A= ​100​145​ ​ 的列空间，就是矩阵A线性变换作用后的对应空间，也就是以矩阵A列的线性组合所构成的空间。

很显然，矩阵A的列空间C(A)就是列向量 [ 1 0 0 ] \left[\begin{array}{l}1 \\ 0 \\ 0\end{array}\right] ​100​ ​ 和 [ 1 4 5 ] \left[\begin{array}{l}1 \\ 4 \\ 5\end{array}\right] ​145​ ​ 所能张成的空间。列空间C(A)的维度为2，也称为列空间C(A)的秩为2。

上述矩阵A与列向量x相乘，有以下性质：

• 经过Ax乘法作用，x的n个n维基向量转换成了n个m维基向量。
• 是矩阵A的行数小于列数时，矩阵A呈现为“矮胖”形态，“矮胖”的矩阵A具有压缩原始空间的作用。
• 矩阵A的行数大于列数时，矩阵A呈现为“瘦高”形态，“瘦高”的矩阵A也可能具有压缩原始空间的作用。
• 矩阵A的行数等于列数时，矩阵A为方阵，方阵A也可能具有压缩原始空间的作用。

总结上述各种情况容易发现，矩阵A中各列的线性相关情况是决定矩阵A是否具有空间压缩作用的关键因素。矩阵A各列张成的空间的维度称为该矩阵A的秩，它等于矩阵A线性无关列的个数。

5.3 理解矩阵乘法的本质

以二维空间为例

在二维空间中，根据矩阵乘法规则，矩阵$\mathbf{A}=\left[\begin{array}{ll}a& b\\ c& d\end{array}\right]$ 与矩阵 $\mathbf{B}=\left[\begin{array}{ll}e& f\\ g& h\end{array}\right]$ 相乘是将左边矩阵的行元素与右边矩阵的列元素分别相乘，然后相加，即

$$\mathbf{AB}=\left[\begin{array}{ll}ae+bg& af+bh\\ ce+dg& cf+dh\end{array}\right]$$

对矩阵乘法本质的理解：矩阵本质上是空间中的某种线性变换，所以矩阵与矩阵相乘可以看作线性变换的复合作用，最后可以用一个新矩阵来表示这种复合线性变换的结果。

6 线性方程组求解的本质

求解线性方程组是一类经常碰到的问题，很多实际问题都可以用线性方程组来进行求解。一个典型的线性方程组如下所示。
$$\{\begin{array}{c}{a}_{11}{x}_1+a_{12}{x}_2+a_{13}{x}_3+\cdots +a_{1n}{x}_n=b_1\\ a_{21}{x}_1+a_{22}{x}_2+a_{23}{x}_3+\cdots +a_{2n}{x}_n=b_2\\ a_{31}{x}_1+a_{32}{x}_2+a_{33}{x}_3+\cdots +a_{3n}{x}_n=b_3\\ ⋮\\ a_{m1}{x}_1+a_{m2}{x}_2+a_{m3}{x}_3+\cdots +a_{mn}{x}_n=b_m\end{array}$$

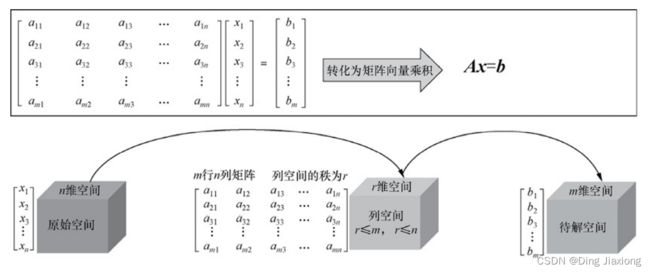
上面的式子包含m个方程、n个未知数，很容易将其转化为矩阵向量乘法的形式，如下所示。

[ a 11 a 12 a 13 ⋯ a 1 n a 21 a 22 a 23 ⋯ a 2 n a 31 a 32 a 33 ⋯ a 3 n ⋮ ⋮ ⋮ ⋮ a m 1 a m 2 a m 3 ⋯ a m n ] [ x 1 x 2 x 3 ⋮ x n ] = [ b 1 b 2 b 3 ⋮ b m ] \left[\begin{array}{ccccc} a_{11} & a_{12} & a_{13} & \cdots & a_{1 n} \\ a_{21} & a_{22} & a_{23} & \cdots & a_{2 n} \\ a_{31} & a_{32} & a_{33} & \cdots & a_{3 n} \\ \vdots & \vdots & \vdots & & \vdots \\ a_{m 1} & a_{m 2} & a_{m 3} & \cdots & a_{m n} \end{array}\right]\left[\begin{array}{c} x_1 \\ x_2 \\ x_3 \\ \vdots \\ x_n \end{array}\right]=\left[\begin{array}{c} b_1 \\ b_2 \\ b_3 \\ \vdots \\ b_m \end{array}\right] ​a11​a21​a31​⋮am1​​a12​a22​a32​⋮am2​​a13​a23​a33​⋮am3​​⋯⋯⋯⋯​a1n​a2n​a3n​⋮amn​​ ​ ​x1​x2​x3​⋮xn​​ ​= ​b1​b2​b3​⋮bm​​ ​

只需令

A = [ a 11 a 12 a 13 ⋯ a 1 n a 21 a 22 a 23 ⋯ a 2 n a 31 a 32 a 33 ⋯ a 3 n ⋮ ⋮ ⋮ ⋮ a m 1 a m 2 a m 3 ⋯ a m n ] , x = [ x 1 x 2 x 3 ⋮ x n ] , b = [ b 1 b 2 b 3 ⋮ b m ] \boldsymbol{A}=\left[\begin{array}{ccccc} a_{11} & a_{12} & a_{13} & \cdots & a_{1 n} \\ a_{21} & a_{22} & a_{23} & \cdots & a_{2 n} \\ a_{31} & a_{32} & a_{33} & \cdots & a_{3 n} \\ \vdots & \vdots & \vdots & & \vdots \\ a_{m 1} & a_{m 2} & a_{m 3} & \cdots & a_{m n} \end{array}\right], \boldsymbol{x}=\left[\begin{array}{c} x_1 \\ x_2 \\ x_3 \\ \vdots \\ x_n \end{array}\right], \boldsymbol{b}=\left[\begin{array}{c} b_1 \\ b_2 \\ b_3 \\ \vdots \\ b_m \end{array}\right] A= ​a11​a21​a31​⋮am1​​a12​a22​a32​⋮am2​​a13​a23​a33​⋮am3​​⋯⋯⋯⋯​a1n​a2n​a3n​⋮amn​​ ​,x= ​x1​x2​x3​⋮xn​​ ​,b= ​b1​b2​b3​⋮bm​​ ​

线性方程组就转化为我们熟悉的矩阵向量乘法形式 $Ax=b$

6.1 理解方程组的解

注意几个空间的含义：

• 原始空间。此处原始空间指代的是原始列向量x所在的空间。由于原始列向量x是一个n维列向量，因此原始空间的维度为n。
• 列空间。矩阵A是m行n列的矩阵，包含n个m维的列向量。这n个m维列向量的线性组合构成的空间就是矩阵A的列空间C(A)，这n个m维列向量中线性无关列向量的个数r就是列空间C(A)的维度，也称为列矩阵A的秩。
• 待解空间。向量b是一个m维的列向量。求解原始未知向量x的时候需要比较向量b所在空间与矩阵A的列空间C(A)之间的关系，因此可以暂时称向量b所在空间为待解空间。待解空间的维度就是列向量b的维度m。

任意线性方程组都可以写成矩阵向量乘法形式 $Ax=b$，只有当向量b可以写成矩阵A各列的线性组合形式时，这个方程组才有解。

求解示意：

【1】一定存在解的情况

【2】一定不存在解的情况

线性方程组一定不存在解的含义是指，假设向量b可以取任意值，这种情况下无法找到未知向量x使得 $Ax=b$ 成立。

【3】一定存在唯一解的情况

当列空间C(A)的维度r等于待解空间的维度m时且等于原始空间的维度 n 时，方程组 $Ax=b$ 一定有唯一解。

【4】一定存在无穷多个解 的情况

$r = m < n $ 时 ，方程组一定有无穷多个解。

【小结】

6.2 寻找解的表达式

步骤：

① 首先找到解空间中的任意点，即任意一个满足方程组 $Ax=b$ 的解，称其为特殊解$x_p$，即 $A{x}_p=b$

② 寻找矩阵A零空间的所有解的表达式，将特殊解 $x_p$ 与矩阵A零空间的所有解相加就是 $Ax=b$ 的解空间。

6.3 逆矩阵的本质

【1】什么是逆矩阵

假设有矩阵 $\mathbf{A}(m\times n)$ 与 $\mathbf{B}(n\times m)$ ，如果 $AB=BA=I$ 【$I$ 为单位矩阵】 ，那么我们就说A为可逆矩阵，B为A的逆矩阵，记为 $\mathbf{B}={\mathbf{A}}^{-1}$。 实际上满足上述定义要求的矩阵A和B一定是方阵

可逆矩阵有着广泛的用处，一个典型的用处就是线性方程组的求解。

例如 $3x+4y+5z=8、5x+6y+7z=9、3x+5y+8z=10$ 所构成的方程组，

可以将系数项 提取出来构成矩阵 A = [ 3 4 5 5 6 7 3 5 8 ] ​ \boldsymbol{A}=\left[\begin{array}{lll}3 & 4 & 5 \\ 5 & 6 & 7 \\ 3 & 5 & 8\end{array}\right] ​ A= ​353​465​578​ ​​

将常数项提取出来构成向量 y = [ 8 9 10 ] y = \left[\begin{array}{l}8 \\ 9 \\ 10\end{array}\right] y= ​8910​ ​ ，则上面的方程组可以表示为$Ax=y$

我们想求解向量x，只需要等式左右两侧同时乘以矩阵A的逆矩阵 $A^{-1}$，就可以得到 $x=A^{-1}y$

我们使用代码来求解

import numpy as np
from scipy import linalg

A = np.array([[3, 4, 5],
              [5, 6, 7],
              [3, 5, 8]])

y = np.array([8, 9, 10])
A_in = linalg.inv(A)
print(A_in)

print("*" * 100)
print(np.dot(A_in, y))

结果为

没毛病，答案确实是这么多。

【2】只有满秩方阵才有逆矩阵

7 行列式的本质

7.1 直观理解行列式

实际上我们可以把行列式看作一个函数，输入的是矩阵$A$，输出的是一个标量det$A$（或记作 |$A$| ）。

行列式的定义域为 $n\times n$ 的矩阵 $A$， 所以行列式一定全部是方阵。

在深入理解行列式之前，先再次明确以下几个概念：

• 矩阵 $A$ 的几何意义是多维空间中的一个线性变换，可以理解为对原来坐标系整体进行某种拉伸或压缩。那么，这种拉伸或者压缩的程度究竟有多大呢？
• 原来坐标系下的“单位面积”或者“单位体积”为 $V1$，经过矩阵$A$拉伸或压缩之后得到的新坐标系的“单位面积”或者“单位体积”为$V2$。
• 矩阵A对原来坐标系的拉伸或者压缩程度可以用（ $V1$ / $V2$ ）来表示，这个比值实际上就是行列式det$A$的值。

举个栗子

以二维空间为例，原始二维空间里面的“单位面积”或者“单位体积”为1×1=1，

经过矩阵 $\mathbf{A}=\left[\begin{array}{ll}2& 0\\ 0& 2\end{array}\right]$ 的线性变换后，坐标系单位向量都拉伸为原来的2倍了，变换后的“单位面积”或者“单位体积”为2×2=4。

原来坐标系下的“单位面积”或者“单位体积”为 |$A$|，经过矩阵A拉伸之后得到的新坐标系的“单位面积”或者“单位体积”为 $V _2 = 4 $ 。

矩阵A对原来坐标系的拉伸程度可以用（ $V1$ / $V2$ ）来表示，这个比值实际上就是行列式det$A$的值，即行列式det$A$的值为4。

行列式的本质就是线性变换所带来的变化率。

7.2 行列式性质

【1】行列式一条重要的性质，$\det \mathbf{A}\mathbf{B}=\det \mathbf{A}\det \mathbf{B}$

【2】“矩阵 $A$ 可逆” 等价于 “det $A$ ≠ 0”

【3】对角矩阵的行列式 $\mathrm{detdiag}\left(a_1,a_2,\cdots ,a_n\right)=a_1,a_2,\cdots ,a_n$

8 最小二乘法本质

8.1 如何求解无解的方程组

$$\{\begin{array}{l}{x}_1+x_2=0\\ 2x_1+x_2=0\\ x_1+x_2=2\end{array}$$

首先将上述线性方程组写成矩阵向量乘法形式 $Ax=b$ ，其中矩阵 A = [ 1 1 2 1 1 1 ] \boldsymbol{A}=\left[\begin{array}{ll}1 & 1 \\ 2 & 1 \\ 1 & 1\end{array}\right] A= ​121​111​ ​ ，向量 b = [ 0 0 2 ] \boldsymbol{b}=\left[\begin{array}{l}0 \\ 0 \\ 2\end{array}\right] b= ​002​ ​

目标是求解一个合理的向量 $\mathbf{x}=\left[\begin{array}{l}{x}_1\\ x_2\end{array}\right]$

这个方程组不存在精确解，按照相关公式求方程组的近似解：

【1】寻找近似解公式中 的矩阵$A$

首先找出列空间C(A)中的所有基向量，这些基向量组成近似解公式中的矩阵A。

因为矩阵 A = [ 1 1 2 1 1 1 ] \boldsymbol{A}=\left[\begin{array}{ll}1 & 1 \\ 2 & 1 \\ 1 & 1\end{array}\right] A= ​121​111​ ​ 的各列线性无关，因此近似解公式中的矩阵A就等于系数矩阵 A = [ 1 1 2 1 1 1 ] \boldsymbol{A}=\left[\begin{array}{ll}1 & 1 \\ 2 & 1 \\ 1 & 1\end{array}\right] A= ​121​111​ ​

【2】代入近似解公式求解
$$\{\begin{array}{l}\hat{\mathbf{x}}={\left({\mathbf{A}}^{\mathrm{T}}\mathbf{A}\right)}^{-1}{\mathbf{A}}^{\mathrm{T}}\mathbf{b}\\ \mathbf{p}=\mathbf{A}{\left({\mathbf{A}}^{\mathrm{T}}\mathbf{A}\right)}^{-1}{\mathbf{A}}^{\mathrm{T}}\mathbf{b}\\ \mathbf{P}=\mathbf{A}{\left({\mathbf{A}}^{\mathrm{T}}\mathbf{A}\right)}^{-1}{\mathbf{A}}^{\mathrm{T}}\end{array}$$

这里直接上代码了

import numpy as np
from scipy import linalg

A = np.array([[1, 1],
              [2, 1],
              [1, 1]])

b = np.array([0, 0, 2])

A_T_A = np.dot(A.T, A)
A_T_A_in = linalg.inv(A_T_A)
x_hat = np.dot(np.dot(A_T_A_in, A.T), b)
p = np.dot(A, x_hat)
p_matrix = np.dot(A, np.dot(A_T_A_in, A.T))

print("近似解x 为:")
print(x_hat)

print("\n投影向量p为:")
print(p)

print("\n 投影矩阵p为:")
print(p_matrix)

运行结果为

9 理解相似矩阵对角化

9.1 相似矩阵的定义

设$A$、$B$都是n阶方阵，若存在可逆矩阵$P$，使 $\mathbf{A}={\mathbf{P}}^{-1}\mathbf{BP}$

则称矩阵A、B是相似矩阵,记为A～B。

这里的可逆矩阵$P$是一个非常重要的矩阵，因为它揭示了“矩阵$A$和$B$实际上描述的是同一个线性变换”这个事实。可逆矩阵$P$描述的就是矩阵$A$所基于的基向量与矩阵$B$所基于的基向量之间的一个变换关系。

9.2 直观理解相似矩阵的本质

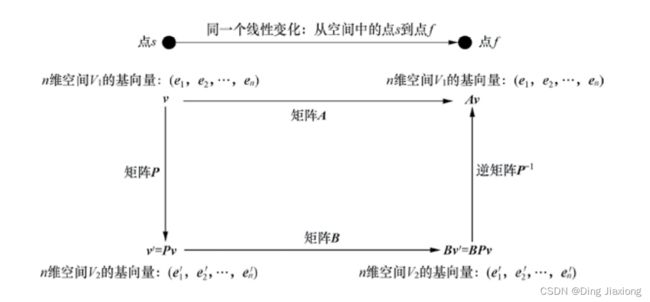
假设空间中有一个初始位置点$s$的向量在线性变换作用下发生了位置变化，从初始位置点$s$变换到了目标位置点$f$，那么上述过程的线性变换可以用矩阵来表示。

我们知道，不同的基底下同一个向量有不同的坐标表示，并且不同基底下空间中同一个向量的同一个位置变换，
用来表示的矩阵也是不同的。那么这些不同基底下，表示同一个向量的同一位置变换的不同矩阵之间存在什么样的关系呢？我们可以从以下角度进行分析。

【1】考虑n 维空间 $V_1$ 的情况

n维空间$V_1$的基向量是 $\left({\mathbf{e}}_1,{\mathbf{e}}_2,\cdots ,{\mathbf{e}}_n\right)$ ，其中有任一初始向量v。

初始向量v在n阶矩阵A的作用下发生了空间位置的变换，变换后的向量为Av，容易知道向量Av仍在n维空间$V_1$中。

其中，关键信息如下：第一，初始位置点s的向量为v；第二，目标位置点f的向量为Av；第三，从初始位置点s变换到了目标位置点f的线性变换矩阵表示为A。

n维空间V1的情况：

【2】考虑n 维空间 $V_2 $ 的情况

n维空间 $V_2 $ 的基向量是 $\left({\mathbf{e}}_1^{\prime },{\mathbf{e}}_2^{\prime },\cdots ,{\mathbf{e}}_n^{\prime }\right)$

上述点s用向量 v’ 来表示，而线性变化从点s变换到点 f’’ 则用矩阵B来表示，变换后的向量为 Bv’，容易知道向量 Bv’ 仍在n维空间 $V_2 $ 中。

其中，关键信息如下：第一，初始位置点s的向量为v’ ；第二，目标位置点f的向量为 Bv’ ；第三，从初始位置点s变换到了目标位置点f的线性变换用矩阵表示为B。

n维空间 $V_2 $ 的情况：

【3】初始向量v 和 v’ 的关系

可逆矩阵P代表n维空间V1中的某个线性变换，在其线性变换作用下n维空间V1中的所有向量都发生了位置变换，变换到了另一个n维空间V2中。

n维空间V1中的基向量 $\left({\mathbf{e}}_1,{\mathbf{e}}_2,\cdots ,{\mathbf{e}}_n\right)$ 变换成了n维空间V2中的一组新的基向量 $\left({\mathbf{e}}_1^{\prime },{\mathbf{e}}_2^{\prime },\cdots ,{\mathbf{e}}_n^{\prime }\right)$

n维空间V1中的任一向量v变换成了n维空间V2中的向量v＇。

容易知道有如下关系。

• 等式关系：$\{\begin{array}{c}{\mathbf{e}}_1^{\prime }=\mathbf{P}{\mathbf{e}}_1\\ {\mathbf{e}}_2^{\prime }=\mathbf{P}{\mathbf{e}}_2\\ {\mathbf{e}}_3^{\prime }=\mathbf{P}{\mathbf{e}}_3\\ ⋮\\ {\mathbf{e}}_n^{\prime }=\mathbf{P}{\mathbf{e}}_n\end{array}$
• 等式关系：v’ = Pv

【4】目标向量Av 和 Bv’ 的关系

空间位置点f的向量在n维空间V1中表示为Av，同一位置点f的向量在n维空间V2中表示为 Bv’，即BPv

10 特征值和特征向量

一个线性变换通常可以由其特征值和特征向量完全描述，特征值和特征向量表达了一个线性变换的最重要的特征。

10.1 特征值和特征向量是什么

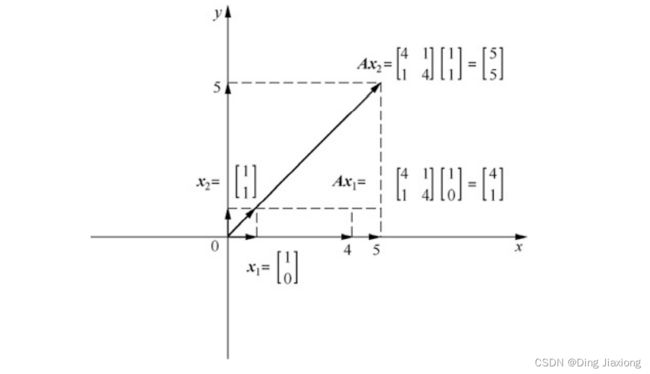
已知矩阵A和向量v，则矩阵向量乘积Av的几何意义是，在向量空间中对向量v进行旋转、平移和拉伸（压缩）等操作，

不难发现矩阵向量乘积Av在其维度空间内对向量v进行线性变换时，有些向量v只会发生数值大小变化（伸缩）而不会发生方向偏移，

这些只发生数值大小变化的向量（如x2）就是该矩阵（如矩阵A）的特征向量，对应向量数值大小变化的倍数就是特征值。