【论文阅读】Graph Transformer Networks
图转换网络
- 摘要
- 1 引言
- 2 相关工作
- 3 方法
-
- 3.1 准备工作
- 3.2 元路径生成
- 3.3 图转换网络
- 4 实验
摘要
GNN已被广泛应用于图的表示学习,并在节点分类和链路预测等任务中取得了最先进的性能。然而,大多数现有的GNN都被设计用来学习固定图和齐次图上的节点表示。当学习由各种类型的节点和边组成的异质图上的表示时,这些限制尤其成为问题。本文提出了能够生成新的图结构的图转换网络(GTN),它涉及识别原始图上未连接的节点之间的有用连接,同时以端到端的方式学习新图上的有效节点表示。GTN的核心层——图形变换层,它学习边类型和复合关系的软选择,从而生成有用的多跳连接,即所谓的元路径。实验表明,GTN在没有领域知识的情况下,根据数据和任务学习新的图结构,并通过卷积在新图上产生强大的节点表示。在没有针对特定领域的图预处理的情况下,GTN在所有三个基准节点分类任务中,与需要从领域知识中预先定义元路径的现状方法相比,都取得了最佳性能。
1 引言
近年来,GNN在图的各种任务中得到了广泛的应用,如图分类、链路预测和节点分类。GNN学习的表示已经被证明可以在各种图数据集中实现最先进的性能,如社交网络、引文网络、大脑的功能结构、推荐系统。GNN利用底层的图结构,通过将节点特征传递给邻居,直接在图上进行卷积操作,或者利用给定图的傅里叶基,即拉普拉斯算子的特征函数,在谱域中进行卷积操作。
然而,大多数GNN的一个局限性是,它们假设操作GNN的图结构是固定的、齐次图。由于上面讨论的图卷积是由固定的图结构决定的,一个有缺失/虚假连接的噪声图会导致图上有错误的邻居而无效卷积。此外,在一些应用中,构建一个图来操作GNN并不简单。例如,一个引文网络有多种类型的节点(如作者、论文、会议)和由其关系定义的边(如作者-论文、论文-会议),它被称为异质图。一个天真的方法是忽略节点/边的类型,把它们当作同质图(一个有一种类型的节点和边的标准图)。这显然是次优的,因为模型不能利用类型信息。最近的一种补救措施是手动设计元路径,即用异质边连接的路径,将异质图转化为由元路径定义的同质图。然后,传统的GNN可以对变换后的齐次图进行操作。这是一个两阶段的方法,需要针对每个问题手动设计元路径。这些元路径的选择会显著影响下游分析的准确性。
本文提出了图转换网络(GTN),它学习将异构输入图转化为针对每个任务有用的元路径图,并以端到端方式学习图上的节点表示。GTN可以看作是空间转换网络的图类比,它明确地学习输入图像或特征的空间转换。将异质图转换为由元路径定义的新图结构的主要挑战是元路径可能具有任意长度和边类型。例如,引文网络中的作者分类可能会受益于这样的元路径,作者-论文-作者(APA)或作者-论文-会议-论文-作者(APCPA)。此外,引文网络是有向图,GNN能操作的相对较少。为了解决这些挑战,我们需要一个模型,基于在异质图中与软选择的边类型连接的复合关系生成新的图结构,并且针对给定的问题通过卷积在学习的图结构上学习节点表示。
贡献:
- 提出了一个新的框架GTN来学习一种新的图结构,其中包括识别有用的元路径和多跳连接,以学习图上有效的节点表示。
- 图的生成具有可解释性,该模型能够为预测提供有效的元路径的见解。
- 证明了由GTN学习的节点表示的有效性,在异质图上的所有三个基准节点分类中,与另外使用领域知识的最先进方法相比,获得了最佳性能。
2 相关工作
GNN。通常分为两类方法:频谱与非频谱方法。基于谱图理论,可以利用给定图的傅里叶基在谱域中进行卷积,后来使用谱图卷积的一阶近似对此进行了简化。非频谱方法利用空间近邻,直接在图上定义卷积操作。例如,一种方法是对不同度的节点应用不同的权重矩阵,另一种方法是一种可学习的聚合函数,它总结了邻居的信息,用于图形表示学习。
基于GNN的节点分类。传统上,手动设计的特征已经被使用,如简单图统计、图核以及来自局部邻居结构的工程特征。这些特征不灵活,性能差。为了克服这一缺点,最近在DeepWalk ,LINE和node2vec中提出了通过图上随机游走的节点表示学习方法,并从深度学习模型(如skip-gram)中获得了一些性能上的改进。然而,所有这些方法都只基于图结构来学习节点表示。这些表示没有针对特定任务进行优化。 由于GNN在表示学习方面取得了显著的成功,GNN可以为给定的任务和数据学习一种强大的表示。为了提高性能或可扩展性,研究了基于谱卷积的广义卷积、邻域注意力机制、次采样和大图的归纳式表示。虽然这些方法显示出突出的结果,但所有这些方法都有一个共同的限制,只处理齐次图。
然而,许多现实世界的问题往往不能用一个单一的齐次图来表示。这些图是一个具有各种类型的节点和边的异质图。由于大多数GNN是为单个齐次图设计的,一个简单的解决方法是一个两阶段的方法。以多种边类型的复合关系的元路径作为预处理,将异质图转化为同质图,然后学习表示。metapath2vec通过使用基于元路径的随机游走来学习图表示,HAN通过将异质图转化为由元路径构建的同质图来学习图表示学习。然而,这些方法由领域专家手动选择元路径,因此可能无法捕获每个问题的所有有意义的关系。另外,元路径的选择也会对性能产生很大影响。与这些方法不同,本文介绍的GTN可以在异质图上进行操作,并根据任务对图进行转换,同时在转换后的图上以端到端方式学习节点表示。
3 方法
GTN的目标是生成新的图结构并同时学习图上的节点表示。不像图上的大多数CNN假设图是给定的那样,GTN 使用多个候选邻接矩阵寻找新的图结构 ,以执行更有效的图卷积和学习更强大的节点表示。学习新的图结构包括识别有用的元路径,即由异构边连接的路径以及多跳连接。
3.1 准备工作
GTN框架的一个输入是具有不同类型的节点和边的多个图结构。设 T v T^v Tv和 T e T^e Te分别是节点类型和边类型的集合。输入图s可以看作是一个异质图 G = ( V , E ) G = (V, E) G=(V,E),其中 V V V是节点集, E E E是可以观察到的边集,还有一个节点类型映射函数 f v : V → T v f_v:V→T^v fv:V→Tv,一个边类型映射函数 f e : E → T e f_e:E→T^e fe:E→Te。每个节点 v i ∈ V v_i∈V vi∈V都有一个节点类型,即 f v ( v i ) ∈ T v f_v(v_i)∈T^v fv(vi)∈Tv。同样地,对于 e i j ∈ E e_{ij}∈E eij∈E, f e ( e i j ) ∈ T e f_e(e_{ij})∈T^e fe(eij)∈Te。当 ∣ T e ∣ = 1 |T^e|=1 ∣Te∣=1和 ∣ T v ∣ = 1 |T^v|=1 ∣Tv∣=1时,它就成为了一个标准图。在本文中,考虑 ∣ T e ∣ > 1 |T^e|>1 ∣Te∣>1的情况。设 N N N表示节点数,即 ∣ V ∣ |V| ∣V∣。异质图可以用 一组邻接矩阵 { A k } k = 1 K \{A _k\}^K_{k=1} {Ak}k=1K 表示,其中 K = ∣ T e ∣ K=|T^e| K=∣Te∣, A k ∈ R N × N A _k∈R^{N×N} Ak∈RN×N是一个邻接矩阵,当从 j j j到 i i i有 k k k类型的边时, A k [ i , j ] A_k[i,j] Ak[i,j]非零。它可以被简写成一个张量 A ∈ R N × N × K A∈R^{N×N×K} A∈RN×N×K。还有一个特征矩阵 X ∈ R N × D X∈R^{N×D} X∈RN×D,这意味着每个节点的输入特征为 D D D维。
元路径
由 p p p表示,是异质图 G G G上由异构的边连接的一条路径,即 v 1 t 1 → v 2 t 2 → . . . t l → v l + 1 \text{ }v_1\text{ }\underrightarrow{t_1}\text{ }v_2\text{ }\underrightarrow{t_2}\text{ }...\text{ }\underrightarrow{t_l}\text{ }v_{l+1} v1 t1 v2 t2 ... tl vl+1,其中 t l ∈ T e t_l∈T^e tl∈Te 表示元路径中的一条 l l l类型的边。它定义了节点 v 1 v_1 v1和 v l + 1 v_{l+1} vl+1之间的一个复合关系 R = t 1 ◦ t 2 … ◦ t l R=t_1◦t_2…◦t_l R=t1◦t2…◦tl,其中 R 1 ◦ R 2 R_1◦R_2 R1◦R2表示关系 R 1 R_1 R1和 R 2 R_2 R2的组成。给定复合关系 R R R或边类型序列 ( t 1 , t 2 , . . . , t l ) (t_1,t_2,...,t_l) (t1,t2,...,tl),元路径 P P P的邻接矩阵 A P A_P AP是通过邻接矩阵的乘法得到的:
![]()
元路径的概念包含了多跳连接,在我们的框架中,新的图结构由邻接矩阵表示。例如,元路径作者-论文-会议(APC)可以表示为 A A P → P P C → C A\text{ }\underrightarrow{AP}\text{ }P\text{ }\underrightarrow{PC}\text{ }C A AP P PC C,通过 A A P A_{AP} AAP和 A P C A_{PC} APC的乘法生成邻接矩阵 A A P C A_{APC} AAPC。
图卷积网络(GCN)
使用GCN以端到端的方式学习节点分类的有用表示。设 H ( l ) H^{(l)} H(l)是GCN中第 l l l层的特征表示,前向传播为:
![]()
其中, A ~ = A + I ∈ R N × N \tilde{A}=A+I∈R^{N×N} A~=A+I∈RN×N是图 G G G的邻接矩阵 A A A加上自连接; D ~ \tilde{D} D~是 A ~ \tilde{A} A~的度矩阵,即 D ~ i i = ∑ i A ~ i j \tilde{D}_{ii}=\sum_i\tilde{A}_{ij} D~ii=∑iA~ij; W ( l ) ∈ R d × d W^{(l)}∈R^{d×d} W(l)∈Rd×d是一个可训练的权值矩阵。我们可以很容易地观察到,整个图上的卷积操作是由给定的图结构决定的,除了节点方面的线性变换 H ( l ) W ( l ) H^{(l)}W^{(l)} H(l)W(l)之外,它是不可学习的。因此,该卷积层可以理解为在图上经过节点线性变换后,由固定卷积后的激活函数 σ σ σ构成。由于我们学习图结构,我们的框架受益于不同的卷积,即 D ~ − 1 2 A ~ D ~ − 1 2 \tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}} D~−21A~D~−21,从学习的多个邻接矩阵中获得。该体系结构将在本节后面进行介绍。对于有向图(即非对称邻接矩阵),(2)式中的 A ~ \tilde{A} A~可以由入度对角矩阵 D ~ − 1 \tilde{D}^{-1} D~−1正则化,最终的图卷积形式变为 H ( l + 1 ) = σ ( D ~ − 1 A ~ H ( l ) W ( l ) ) H^{(l+1)}=σ(\tilde{D}^{-1}\tilde{A}H^{(l)}W^{(l)}) H(l+1)=σ(D~−1A~H(l)W(l))。
3.2 元路径生成
以前的工作需要手动定义元路径,并在元路径图上执行图形神经网络。相反,GTN学习给定数据和任务的元路径,并在学习到的元路径图上操作图的卷积。这给了一个找到更有用的元路径的机会,并使用多个元路径图导致几乎不同的图卷积。
在图转换(GT)层中新的元路径图生成包括两部分,如图1所示。首先,GT层从候选邻接矩阵 A \mathbb{A} A中软选择两个图结构 Q 1 Q_1 Q1和 Q 2 Q_2 Q2。然后,它通过两个关系的组合(即两个邻接矩阵 Q 1 Q_1 Q1和 Q 2 Q_2 Q2的矩阵乘法)来学习一个新的图形结构。

- 此图即表示GT层,它先从tensor A \mathbb{A} A(每一片就是一种边类型)中用权重选择adjacency matrices(即边类型)。权重选择的方式也可以理解成卷积,卷积后的两个matrices分别是两个图解构,表示为 Q 1 Q_1 Q1和 Q 2 Q_2 Q2。
- 选择matrices的两个卷积核是用softmax计算得出的(比如图中例子,一个卷积核说取最前面的matrices,一个卷积核说取最后面那个matrices),但实际上是带有权重分配的。
- 然后再将两个matrices组成新的图结构 A ( 1 ) A^{(1)} A(1)(即两个邻接矩阵的矩阵乘法, Q 1 Q 2 Q_1Q_2 Q1Q2)。
邻接矩阵 Q Q Q的选择方式如下:
![]()
其中, ϕ \phi ϕ是卷积层, W ϕ ∈ R 1 × 1 × K W_\phi∈\pmb{R}^{1×1×K} Wϕ∈RRR1×1×K是 ϕ \phi ϕ的参数。即 Q Q Q是将 A \mathbb{A} A和权重参数 W ϕ W_\phi Wϕ送去卷积层卷积得到的。
每一个 Q i Q_i Qi可以表示成:
∑ t l ∈ T e α t l ( l ) A t l \sum_{t_l∈T^e}\alpha_{t_l}^{(l)}A_{t_l} tl∈Te∑αtl(l)Atl
其中, T e T^e Te是边的类型集合, α t l ( l ) \alpha_{t_l}^{(l)} αtl(l)是第 l l l 种边类型 t l t_l tl 在第 l l l 层的权重。
以图1为例:
T e T^e Te有4个 { t 1 , t 2 , t 3 , t 4 } \{t_1,t_2,t_3,t_4\} {t1,t2,t3,t4},即对应4层matrices: { A 1 , A 2 , A 3 , A 4 } \{A_1,A_2,A_3,A_4\} {A1,A2,A3,A4}, W ϕ = { α 1 , α 2 , α 3 , α 4 } W_\phi=\{\alpha_1,\alpha_2,\alpha_3,\alpha_4\} Wϕ={α1,α2,α3,α4}。
得到 Q 1 Q_1 Q1和 Q 2 Q_2 Q2后,通过两个邻接矩阵的矩阵乘法 Q 1 Q 2 Q_1Q_2 Q1Q2得到新的元路径邻接矩阵。为了提高数值稳定性,通过该矩阵的度矩阵将归一化,即 A ( l ) = D − 1 Q 1 Q 2 A^{(l)}=D^{-1}Q_1Q_2 A(l)=D−1Q1Q2。
现在,我们需要检查GTN是否可以学习关于边类型和路径长度的任意元路径。 任意长度 l l l元路径的邻接矩阵可以表示为:

其中 A P A_P AP表示元路径的邻接矩阵, T e T^e Te是边的类型集合, α t l ( l ) \alpha_{t_l}^{(l)} αtl(l)是第 l l l 个GT层上边类型 t l t_l tl 的权重。当 α α α不是one-hot向量时, A P A_P AP可以看作是所有长度为 l l l 元路径邻接矩阵的加权和。因此,一个 l l l个GT层的堆栈可以学习任意长度的 l l l元路径图结构,如图2所示。这种结构的一个问题是,添加GT层总是增加元路径的长度,而不允许使用原始的边。在一些应用中,长元路径和短元路径都很重要。为了学习包含原始边的短元路径和长元路径(如果全部按照图中的生成,则每一条元路径都是基于原始边所生成的,也就忽略了原始边的本身的特征),我们在 A \mathbb{A} A中加入单位矩阵 I I I,即 A 0 = I A_0=I A0=I。这个技巧允许GTN学习任何长度的元路径,当 l l l个GT层堆叠时,元路径的长度可达 l + 1 l+1 l+1。

3.3 图转换网络
为了同时生成多种类型的元路径,图1中 1 × 1 1×1 1×1卷积的输出通道设置为 C C C。然后,GT层产生一组元路径,中间邻接矩阵 Q 1 Q_1 Q1和 Q 2 Q_2 Q2成为邻接张量 Q 1 Q_1 Q1和 Q 2 ∈ R N × N × C Q_2∈\pmb{R}^{N×N×C} Q2∈RRRN×N×C,如图2所示。通过多个不同的图结构学习不同的节点表示是有益的。在 l l l个GT层堆叠之后,将GCN应用于元路径张量 A ( l ) ∈ R N × N × C \mathbb{A}^{(l)}∈\pmb{R}^{N×N×C} A(l)∈RRRN×N×C的每个通道,并将多个节点的表示连接起来:
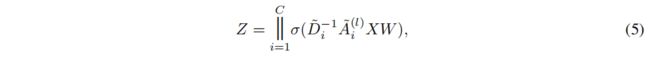
其中, ∣ ∣ || ∣∣为连接运算符, C C C表示通道数, A ~ i ( l ) = A i ( l ) + I \widetilde{A}_i^{(l)}=A_i^{(l)}+I A i(l)=Ai(l)+I表示张量 A ( l ) \mathbb{A}^{(l)} A(l)的第 l l l个通道的邻接矩阵, D ~ i \widetilde{D}_i D i是 A ~ i ( l ) \widetilde{A}_i^{(l)} A i(l)的度矩阵, W ∈ R d × d W∈\pmb{R}^{d×d} W∈RRRd×d是跨通道共享的可训练权重矩阵, X ∈ R N × d X∈\pmb{R}^{N×d} X∈RRRN×d是一个特征矩阵。
Z Z Z包含来自 C C C个不同的元路径图的节点表示,该图具有可变性、长度最多为 l + 1 l+1 l+1。它用于顶部的节点分类。损失函数是具有ground truth标签的节点上的标准交叉熵。
4 实验
参考博客:https://zhuanlan.zhihu.com/p/151065680
https://blog.csdn.net/qq_44015059/article/details/109248774
https://blog.csdn.net/mirrorssssssss/article/details/103797829