【GAMES101】作业3(提高)与法线贴图原理和渲染管线框架分析
目录
- 1. 作业描述
-
- 1.1 任务
- 1.2 编译与运行
- 1.3 框架与代码说明
- 2. 需要注意的问题
- 3. 解
-
- 3.1 rasterize_triangle
- 3.2 get_projection_matrix
- 3.3 texture_fragment_shader
- 3.4 phong_fragment_shader
- 3.5 bump mapping
-
- 3.5.1 bump_fragment_shader
- 3.5.2 displacement_fragment_shader
- 4. 效果
-
- 4.1 normal shader
- 4.2 phong fragment shader
- 4.3 texture fragment shader
- 4.4 displacement fragment shader
- 4.5 bump fragment shader
- 5. 提高
-
- 5.1 双线性插值
-
- 5.1.1 代码
- 5.1.2 效果
- 5.2 其他模型
-
- 5.2.1 修改部分
- 5.2.2 效果
- 6. 渲染管线
-
- 6.1 输入处理
- 6.2 顶点、三角形处理
- 6.3 光栅化、片元处理、帧缓冲处理
- 6.4 显示
- 7. 附件
1. 作业描述
1.1 任务
在这次编程任务中,我们会进一步模拟现代图形技术。我们在代码中添加了Object Loader(用于加载三维模型), Vertex Shader 与 Fragment Shader,并且支持了纹理映射。
而在本次实验中,你需要完成的任务是:
- 修改函数 rasterize_triangle(const Triangle& t) in rasterizer.cpp: 在此 处实现与作业 2 类似的插值算法,实现法向量、颜色、纹理颜色的插值。
- 修改函数 get_projection_matrix() in main.cpp: 将你自己在之前的实验中 实现的投影矩阵填到此处,此时你可以运行 ./Rasterizer output.png normal 来观察法向量实现结果。
- 修改函数 phong_fragment_shader() in main.cpp: 实现 Blinn-Phong 模型计 算 Fragment Color.
- 修改函数 texture_fragment_shader() in main.cpp: 在实现 Blinn-Phong 的基础上,将纹理颜色视为公式中的 kd,实现 Texture Shading Fragment Shader.
- 修改函数 bump_fragment_shader() in main.cpp: 在实现 Blinn-Phong 的 基础上,仔细阅读该函数中的注释,实现 Bump mapping.
- 修改函数 displacement_fragment_shader() in main.cpp: 在实现 Bump mapping 的基础上,实现 displacement mapping.
1.2 编译与运行
在课程提供的虚拟机上,下载本次实验的基础代码之后,请在 SoftwareRasterizer 目录下按照如下方式构建程序:
1 $ mkdir build
2 $ cd . / build
3 $ cmake . .
4 $ make
这将会生成命名为 Rasterizer 的可执行文件。使用该可执行文件时,你传入的第二个参数将会是生成的图片文件名,而第三个参数可以是如下内容:
• texture: 使用代码中的 texture shader. 使用举例: ./Rasterizer output.png texture
• normal: 使用代码中的 normal shader. 使用举例: ./Rasterizer output.png normal
• phong: 使用代码中的 blinn-phong shader. 使用举例: ./Rasterizer output.png phong
• bump: 使用代码中的 bump shader. 使用举例: ./Rasterizer output.png bump
• displacement: 使用代码中的 displacement shader. 使用举例: ./Rasterizer output.png displacement
当你修改代码之后,你需要重新 make 才能看到新的结果。
1.3 框架与代码说明
相比上次实验,我们对框架进行了如下修改:
- 我们引入了一个第三方.obj 文件加载库来读取更加复杂的模型文件,这部分库文件在 OBJ_Loader.h file. 你无需详细理解它的工作原理,只需知道这个库将会传递给我们一个被命名被 TriangleList 的 Vector,其中每个三角形都有对应的点法向量与纹理坐标。此外,与模型相关的纹理也将被一同加载。
注意:如果你想尝试加载其他模型,你目前只能手动修改模型路径。- 我们引入了一个新的 Texture 类以从图片生成纹理,并且提供了查找纹理颜色的接口:Vector3f getColor(float u, float v)
- 我们创建了 Shader.hpp 头文件并定义了 fragment_shader_payload,其中包括了 Fragment Shader 可能用到的参数。目前 main.cpp 中有三个 FragmentShader,其中 fragment_shader 是按照法向量上色的样例 Shader,其余两个将由你来实现。
- 主渲染流水线开始于 rasterizer::draw(std::vector &TriangleList).我们再次进行一系列变换,这些变换一般由 Vertex Shader 完成。在此之后,我们调用函数 rasterize_triangle.
- rasterize_triangle 函数与你在作业 2 中实现的内容相似。不同之处在于被设定的数值将不再是常数,而是按照 Barycentric Coordinates 对法向量、颜色、纹理颜色与底纹颜色 (Shading Colors)进行插值。回忆我们上次为了计算z value 而提供的 [alpha, beta,gamma],这次你将需要将其应用在其他参数的插值上。你需要做的是计算插值后的颜色,并将 Fragment Shader 计算得到的颜色写入framebuffer,这要求你首先使用插值得到的结果设置 fragment shader payload,并调用 fragment shader 得到计算结果。
2. 需要注意的问题
当所有需要修改的地方都没有问题了,但是运行程序时出现了访问越界的提示,大概率是获取纹理颜色的时候坐标越界了(这个问题当初卡了我好久):
Eigen::Vector3f getColor(float u, float v)
{
auto u_img = u * width;
auto v_img = (1 - v) * height;
auto color = image_data.at<cv::Vec3b>(v_img, u_img);
return Eigen::Vector3f(color[0], color[1], color[2]);
}
一般情况下,我们默认纹理图坐标范围是[0, 1]^2,而这里在定义getcolor方法的时候似乎是忘记了对坐标范围的限制,所以要在前面加上两句对坐标的限制:
u = std::fmin(1, std::fmax(u, 0));
v = std::fmin(1, std::fmax(v, 0));
调试时也有小技巧,写完每一个shader的时候可以单独运行调试,方便定位问题,不用全部写完再运行
3. 解
3.1 rasterize_triangle
这部分相较于上次作业来说并没有太大的修改,就是在计算出深度值以后判断遮挡,然后再插值计算法向量、颜色、纹理颜色与底纹颜色等传入fragment_shader_payload (因为是fragment shader,所以是用三角形三个顶点插值的方法),由它的active_shader来计算该点最后的颜色(本来想沿用上次作业的MSAA来抗锯齿,但是效果不好,而且运行还慢,有兴趣的朋友可以自己添加插值计算部分试一下效果:作业2)
void rst::rasterizer::rasterize_triangle(const Triangle& t, const std::array<Eigen::Vector3f, 3>& view_pos)
{
auto v = t.toVector4();
Vector3f color;
float alpha, beta, gamma, lmin=INT_MAX, rmax=INT_MIN, tmax=INT_MIN, bmin=INT_MAX, id;
for(auto &k:v){//找到bounding box的边界坐标
lmin = int(std::min(lmin,k.x()));
rmax = std::max(rmax,k.x());rmax = rmax == int(rmax) ? int(rmax)-1 : rmax;
tmax = std::max(tmax,k.y());tmax = tmax == int(tmax) ? int(tmax)-1 : tmax;
bmin = int(std::min(bmin,k.y()));
}
for(float i = lmin; i <= rmax; i++){
for(float j = bmin; j <= tmax; j++){//遍历bounding box像素
id = get_index(i,j);
if(insideTriangle(i+0.5, j+0.5, t.v)){//如果像素在三角形内
// If so, use the following code to get the interpolated z value.
std::tie(alpha, beta, gamma) = computeBarycentric2D(i+0.5, j+0.5, t.v);
float w_reciprocal = 1.0/(alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
z_interpolated *= w_reciprocal;
if (-z_interpolated < depth_buf[id]){//如果该像素的深度更小,更新像素深度、颜色表
auto interpolated_color = interpolate(alpha, beta, gamma, t.color[0], t.color[1], t.color[2], 1);//颜色插值
auto interpolated_normal = interpolate(alpha, beta, gamma, t.normal[0], t.normal[1], t.normal[2], 1).normalized();//法向量插值
auto interpolated_texcoords = interpolate(alpha, beta, gamma, t.tex_coords[0], t.tex_coords[1], t.tex_coords[2], 1);//纹理坐标插值
auto interpolated_shadingcoords = interpolate(alpha, beta, gamma, view_pos[0], view_pos[1], view_pos[2], 1);//着色点坐标插值
fragment_shader_payload payload(interpolated_color, interpolated_normal.normalized(), interpolated_texcoords, texture ? &*texture : nullptr);//将插值属性传入fragment_shader_payload
payload.view_pos = interpolated_shadingcoords;//传入原顶点坐标
depth_buf[id] = -z_interpolated;
frame_buf[id] = fragment_shader(payload);//使用shader计算颜色
// TODO : set the current pixel (use the set_pixel function) to the color of the triangle (use getColor function) if it should be painted.
set_pixel({i,j}, frame_buf[id]);
}
}
}
}
}
3.2 get_projection_matrix
之前的作业一直存在上下左右颠倒的问题,因为只是涉及左右手系的转换,所以没有管,但是这次的作业不转换过来的话不太美观,所以还是转换一下吧,这里只用把高度乘以一个负号即可,因为宽度由高度计算而来,就不用管了。
(注意:get_projection_matrix 中的 eye_fov 应该被转化为弧度制)
Eigen::Matrix4f get_projection_matrix(float eye_fov, float aspect_ratio, float zNear, float zFar)
{
// TODO: Use the same projection matrix from the previous assignments
Eigen::Matrix4f projection = Eigen::Matrix4f::Identity();
Eigen::Matrix4f proj, ortho;
eye_fov = (eye_fov/180.0)*MY_PI;
proj << zNear, 0, 0, 0,
0, zNear, 0, 0,
0, 0, zNear + zFar, -zNear * zFar,
0, 0, 1, 0;//透视投影矩阵
double w, h, z;
h = -zNear * tan(eye_fov / 2) * 2;
w = h * aspect_ratio;
z = zFar - zNear;
ortho << 2 / w, 0, 0, 0,
0, 2 / h, 0, 0,
0, 0, 2 / z, -(zFar+zNear) / 2,
0, 0, 0, 1;//正交投影矩阵,因为在观测投影时x0y平面视角默认是中心,所以这里的正交投影就不用平移x和y了
projection = ortho * proj * projection;
return projection;
}
通过rasterize_triangle把各项属性传入fragment_shader_payload以后,各类shader就可以调用这些属性来进行着色
3.3 texture_fragment_shader
texture_fragment_shader的主要难点在于blinn-phong模型的实现,前面的纹理颜色获取其实很简单,就是利用传入的payload的texture属性,调用它的getcolor()方法以获取纹理颜色,这里我用的是自定义的双线性插值的方法getColorBilinear()。
而blinn-phong模型的实现其实也很简单,分三部分计算,分别是环境光、漫反射和高光。
①环境光在这里简单看作一个常数,为了保证模型可见处不是全黑的,更贴近日常经验,也更方便观看(注意,这里的计算结果是一个三维颜色向量,所以计算时是用了cwiseProduct()方法来实现点对点乘):

②漫反射的反射光是向四面八方反射的,与观测角度和距离无关,只与传播距离衰减,入射角和物体表面法向量有关(影响光强),比如我们看墙面和桌面时就是这样的,计算时漫反射的系数和物体的底纹颜色有关。

③高光在光滑物体表面比较常见,因为是一种近似于镜面反射的光,所以一般只有入射角接近反射角时才容易看到高光,这里为优化计算斜率,使用入射角和观测角的半角与法向量进行比较判断高光。

计算时要注意,入射角和观测角一定要归一化normalized(),同理,半角和法向量也是,计算结果错误时看下这里是不是没有归一化
根据draw函数里面的定义,传入payload的三个顶点的坐标view_pos是只经过MV变换,没有经过P投影变换,说明shader里面默认都是在相机坐标系而不是世界坐标系下计算的,不要再多余对坐标转换了!
Eigen::Vector3f texture_fragment_shader(const fragment_shader_payload& payload)
{
Eigen::Vector3f return_color = {0, 0, 0};
if (payload.texture)//判断是否有纹理传入
{
// TODO: Get the texture value at the texture coordinates of the current fragment
return_color = payload.texture->getColorBilinear(payload.tex_coords.x(), payload.tex_coords.y());
}
Eigen::Vector3f texture_color;
texture_color << return_color.x(), return_color.y(), return_color.z();
Eigen::Vector3f ka = Eigen::Vector3f(0.005, 0.005, 0.005);
Eigen::Vector3f kd = texture_color / 255.f;
Eigen::Vector3f ks = Eigen::Vector3f(0.7937, 0.7937, 0.7937);//环境光、漫反射和高光系数
auto l1 = light{{20, 20, 20}, {500, 500, 500}};
auto l2 = light{{-20, 20, 0}, {500, 500, 500}};//灯光强度、位置
std::vector<light> lights = {l1, l2};
Eigen::Vector3f amb_light_intensity{10, 10, 10};//环境光强度
Eigen::Vector3f eye_pos{0, 0, 10};//眼睛观测位置
float p = 150;
Eigen::Vector3f color = texture_color;//纹理颜色
Eigen::Vector3f point = payload.view_pos;//着色点坐标
Eigen::Vector3f normal = payload.normal;//着色点法向量
Eigen::Vector3f amb, dif, spe, l, v;
Eigen::Vector3f result_color = {0, 0, 0};
for (auto& light : lights)
{
// TODO: For each light source in the code, calculate what the *ambient*, *diffuse*, and *specular*
// components are. Then, accumulate that result on the *result_color* object.
l = (light.position - point).normalized();
v = (eye_pos - point).normalized() + l;
dif = kd.cwiseProduct(light.intensity / ((light.position - point).dot(light.position - point))) * std::fmax(0, normal.dot(l));
spe = ks.cwiseProduct(light.intensity / ((light.position - point).dot(light.position - point))) * pow(std::fmax(0, normal.dot(v.normalized())), p);
amb = ka.cwiseProduct(amb_light_intensity);
result_color += (dif + spe + amb);
}
return result_color * 255.f;
}
3.4 phong_fragment_shader
和texture_fragment_shader基本一样,只是这里的颜色是模型自带颜色,不是纹理颜色
Eigen::Vector3f phong_fragment_shader(const fragment_shader_payload& payload)
{
Eigen::Vector3f ka = Eigen::Vector3f(0.005, 0.005, 0.005);
Eigen::Vector3f kd = payload.color;
Eigen::Vector3f ks = Eigen::Vector3f(0.7937, 0.7937, 0.7937);
auto l1 = light{{20, 20, 20}, {500, 500, 500}};
auto l2 = light{{-20, 20, 0}, {500, 500, 500}};
std::vector<light> lights = {l1, l2};
Eigen::Vector3f amb_light_intensity{10, 10, 10};
Eigen::Vector3f eye_pos{0, 0, 10};
float p = 150;
Eigen::Vector3f color = payload.color;
Eigen::Vector3f point = payload.view_pos;
Eigen::Vector3f normal = payload.normal;
Eigen::Vector3f result_color = {0, 0, 0};
Eigen::Vector3f amb, dif, spe, l, v;
for (auto& light : lights)
{
// TODO: For each light source in the code, calculate what the *ambient*, *diffuse*, and *specular*
// components are. Then, accumulate that result on the *result_color* object.
l = (light.position - point).normalized();
v = (eye_pos - point).normalized() + l;
dif = kd.cwiseProduct(light.intensity / ((light.position - point).dot(light.position - point))) * std::fmax(0, normal.dot(l));
spe = ks.cwiseProduct(light.intensity / ((light.position - point).dot(light.position - point))) * pow(std::fmax(0, normal.dot(v.normalized())), p);
amb = ka.cwiseProduct(amb_light_intensity);
result_color += (dif + spe + amb);
}
return result_color * 255.f;
}
3.5 bump mapping
在作业三更正公告里面助教提到了:
 bump_mapping其实就是改变物体表面法向量,使得最终呈现出凹凸感,在后面displacement_fragment_shader的实现效果也可以看出来,模型的高光出现在了一些之前没有出现过的地方,证明bump_mapping成功,这里只用照着注释写代码就行了,其余的注意事项也在图里,原理会在下面的课上解释,不想提前看原理的可以跳过下面这部分了。
bump_mapping其实就是改变物体表面法向量,使得最终呈现出凹凸感,在后面displacement_fragment_shader的实现效果也可以看出来,模型的高光出现在了一些之前没有出现过的地方,证明bump_mapping成功,这里只用照着注释写代码就行了,其余的注意事项也在图里,原理会在下面的课上解释,不想提前看原理的可以跳过下面这部分了。
首先我们看到bump_mapping所使用到的纹理贴图:

这副纹理图实际上是利用颜色记录了每个纹理像素的高度差(并没有实际改变高度,只是扰乱了法向量的计算让它看起来有高度差)
有了高度差怎么算被扰乱的法向量呢?我们先来看一个二维的例子:

我们设一个点上原本的法向量为(0,1),那么要求它的新法向量就要知道这个点上高度的导数(即它的微分dp),利用求得的微分,我么就可以得到这点的切向量(1,dp),得到了切向量,它的法向量就是切向量逆时针旋转90°,根据旋转公式,可得新法向量为(-dp,1).normalized()
求得了二维的,三维的自然也就是照猫画虎了:

最终得到法向量为(-dp/du,-dp/dv,1).normalized()
但是有个问题,我们这里一开始都是假设的该点原本的法向量是(0,0,1),证明是在以该点为原点的切向空间计算的结果,想要得到在世界坐标系下的法向量的话肯定还要经过一次转换,那有个怎么做呢?答案就是TBN矩阵:

其实TBN类似的坐标系转换矩阵我们在Lecture 04里面提到过,就是相机View转换的时候:
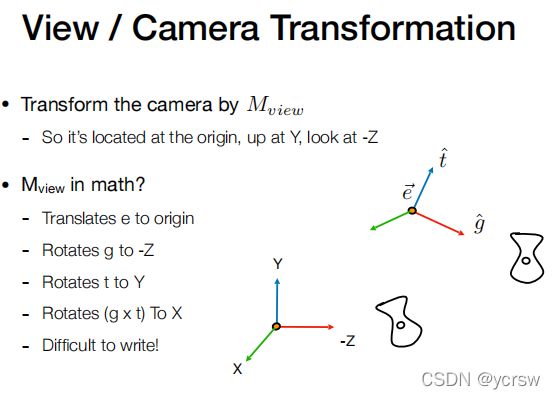

那么同理,我们求出了切向空间的三个归一化坐标轴向量T(Tangent切线),N是Normal法线不用求,B是Bitangent副切线,T叉乘N即可求得,接下来直接代入矩阵与求得的法向量相乘即可
3.5.1 bump_fragment_shader
Eigen::Vector3f bump_fragment_shader(const fragment_shader_payload& payload)
{
Eigen::Vector3f ka = Eigen::Vector3f(0.005, 0.005, 0.005);
Eigen::Vector3f kd = payload.color;
Eigen::Vector3f ks = Eigen::Vector3f(0.7937, 0.7937, 0.7937);
auto l1 = light{{20, 20, 20}, {500, 500, 500}};
auto l2 = light{{-20, 20, 0}, {500, 500, 500}};
std::vector<light> lights = {l1, l2};
Eigen::Vector3f amb_light_intensity{10, 10, 10};
Eigen::Vector3f eye_pos{0, 0, 10};
float p = 150;
Eigen::Vector3f color = payload.color;
Eigen::Vector3f point = payload.view_pos;
Eigen::Vector3f normal = payload.normal;
float kh = 0.2, kn = 0.1;
// TODO: Implement bump mapping here
// Let n = normal = (x, y, z)
// Vector t = (x*y/sqrt(x*x+z*z),sqrt(x*x+z*z),z*y/sqrt(x*x+z*z))
// Vector b = n cross product t
// Matrix TBN = [t b n]
// dU = kh * kn * (h(u+1/w,v)-h(u,v))
// dV = kh * kn * (h(u,v+1/h)-h(u,v))
// Vector ln = (-dU, -dV, 1)
// Normal n = normalize(TBN * ln)
float x, y, z;
Vector3f t, b;
x = normal.x(), y = normal.y(), z = normal.z();
t << x * y / sqrt(x * x + z * z), sqrt(x * x + z * z), z * y / sqrt(x * x + z * z);
b = normal.cross(t);
Matrix3f TBN;
TBN << t.x(), b.x(), normal.x(),
t.y(), b.y(), normal.y(),
t.z(), b.z(), normal.z();
float u, v, w, h;
u = payload.tex_coords.x();
v = payload.tex_coords.y();
w = payload.texture->width;
h = payload.texture->height;
float dU = kh * kn * (payload.texture->getColorBilinear(u + 1.0 / w,v).norm() - payload.texture->getColorBilinear(u,v).norm());
float dV = kh * kn * (payload.texture->getColorBilinear(u,v + 1.0 / h).norm() - payload.texture->getColorBilinear(u,v).norm());
Vector3f ln;
ln << -dU, dV, 1;
normal = (TBN * ln).normalized();
Eigen::Vector3f result_color = {0, 0, 0};
result_color = normal;
return result_color * 255.f;
}
3.5.2 displacement_fragment_shader
displacement mapping是比bump mapping更进一步的做法,因为bump mapping只是改变了法向量使得视觉上出现了凹凸,但是实际上会在边缘露馅,而位移贴图则是真的让三角形顶点进行了唯一,只不过有代价,就是必须保证三角形顶点足够细致:

Eigen::Vector3f displacement_fragment_shader(const fragment_shader_payload& payload)
{
Eigen::Vector3f ka = Eigen::Vector3f(0.005, 0.005, 0.005);
Eigen::Vector3f kd = payload.color;
Eigen::Vector3f ks = Eigen::Vector3f(0.7937, 0.7937, 0.7937);
auto l1 = light{{20, 20, 20}, {500, 500, 500}};
auto l2 = light{{-20, 20, 0}, {500, 500, 500}};
std::vector<light> lights = {l1, l2};
Eigen::Vector3f amb_light_intensity{10, 10, 10};
Eigen::Vector3f eye_pos{0, 0, 10};
float p = 150;
Eigen::Vector3f color = payload.color;
Eigen::Vector3f point = payload.view_pos;
Eigen::Vector3f normal = payload.normal;
float kh = 0.2, kn = 0.1;
// TODO: Implement displacement mapping here
// Let n = normal = (x, y, z)
// Vector t = (x*y/sqrt(x*x+z*z),sqrt(x*x+z*z),z*y/sqrt(x*x+z*z))
// Vector b = n cross product t
// Matrix TBN = [t b n]
// dU = kh * kn * (h(u+1/w,v)-h(u,v))
// dV = kh * kn * (h(u,v+1/h)-h(u,v))
// Vector ln = (-dU, -dV, 1)
// Position p = p + kn * n * h(u,v)
// Normal n = normalize(TBN * ln)
float x, y, z;
Vector3f t, b;
x = normal.x(), y = normal.y(), z = normal.z();
t << x * y / sqrt(x * x + z * z), sqrt(x * x + z * z), z * y / sqrt(x * x + z * z);
b = normal.cross(t);
Matrix3f TBN;
TBN << t.x(), b.x(), normal.x(),
t.y(), b.y(), normal.y(),
t.z(), b.z(), normal.z();
float u, v, w, h;
u = payload.tex_coords.x();
v = payload.tex_coords.y();
w = payload.texture->width;
h = payload.texture->height;
float dU = kh * kn * (payload.texture->getColorBilinear(u + 1.0 / w,v).norm() - payload.texture->getColorBilinear(u,v).norm());
float dV = kh * kn * (payload.texture->getColorBilinear(u,v + 1.0 / h).norm() - payload.texture->getColorBilinear(u,v).norm());
Vector3f ln;
ln << -dU, dV, 1;
point += kn * normal * payload.texture->getColorBilinear(u,v).norm();//这一步就是区分displacement与bump的关键,位移
normal = (TBN * ln).normalized();
Eigen::Vector3f result_color = {0, 0, 0};
Eigen::Vector3f amb, dif, spe, l, v1;
for (auto& light : lights)
{
// TODO: For each light source in the code, calculate what the *ambient*, *diffuse*, and *specular*
// components are. Then, accumulate that result on the *result_color* object.
l = (light.position - point).normalized();
v1 = (eye_pos - point).normalized() + l;
dif = kd.cwiseProduct(light.intensity / ((light.position - point).dot(light.position - point))) * std::fmax(0, normal.dot(l));
spe = ks.cwiseProduct(light.intensity / ((light.position - point).dot(light.position - point))) * pow(std::fmax(0, normal.dot(v1.normalized())), p);
amb = ka.cwiseProduct(amb_light_intensity);
result_color += (dif + spe + amb);
}
return result_color * 255.f;
}
4. 效果
最终效果与实例基本一致
4.1 normal shader
根据normal shader部分的代码,应该是将点的法向量直接可视化为颜色(因为都是三维)

4.2 phong fragment shader
4.3 texture fragment shader
4.4 displacement fragment shader
4.5 bump fragment shader
5. 提高
根据assignment3文档中提到的两个bouns:
①尝试更多模型: 找到其他可用的.obj 文件,提交渲染结果并把模型保存在 /models 目录下。这些模型也应该包含 Vertex Normal 信息。
②使用双线性插值进行纹理采样, 在 Texture类中实现一个新方法 Vector3f getColorBilinear(float u, float v) 并通过 fragment shader 调用它。为了使双线性插值的效果更加明显,你应该考虑选择更小的纹理图。请同时提交纹理插值与双线性纹理插值的结果,并进行比较。
5.1 双线性插值
首先是双线性插值,它的原理很简单,就是利用指定点周围四个纹理像素的颜色进行线性插值,首先在水平方向上利用线性插值计算出u0和u1上下两个点的颜色,然后在垂直方向上利用u0和u1线性插值出所求点的颜色,这样就达成了像素间颜色随距离渐变的平滑过渡的效果,具体见下图:

5.1.1 代码
定义在texture.hpp中
Eigen::Vector3f getColorBilinear(float u, float v){
float w1 = int(u * width), h1 = int(v * height);
float w2 = w1 + 1, h2 = h1;
float w3 = w1, h3 = h1 + 1;
float w4 = w1 + 1, h4 = h1 + 1;
Eigen::Vector3f color1, color2, color3, color4, color5, color6, color;
color1 = getColor(w1 / width, h1 / height);
color2 = getColor(w2 / width, h2 / height);
color3 = getColor(w3 / width, h3 / height);
color4 = getColor(w4 / width, h4 / height);
color5 = color1 + (color2 - color1) * (u * width - w1);
color6 = color3 + (color4 - color3) * (u * width - w1);
color = color5 + (color6 - color5) * (v * height - h1);
return color;
}
5.1.2 效果
为更好的展示效果,这里用bump shader自带的hamp图来对比:
插值前:

插值后:

可以明显看到,在经过双线性插值以后,纹理的过渡变得更加的平滑了
5.2 其他模型
这部分我原本以为只用修改读取文件的路径即可,但是实际效果不尽如人意,不知道是不是给的模型里面纹理坐标对应的不太对的原因,希望有知道的朋友可以帮忙解答一下
5.2.1 修改部分
main.cpp
objl::Loader Loader;
std::string obj_path = "../models/rock/";
// Load .obj File
bool loadout = Loader.LoadFile("../models/rock/rock.obj");
...
if (argc == 3 && std::string(argv[2]) == "texture")
{
std::cout << "Rasterizing using the texture shader\n";
active_shader = texture_fragment_shader;
texture_path = "rock.png";
r.set_texture(Texture(obj_path + texture_path));
}
5.2.2 效果
6. 渲染管线
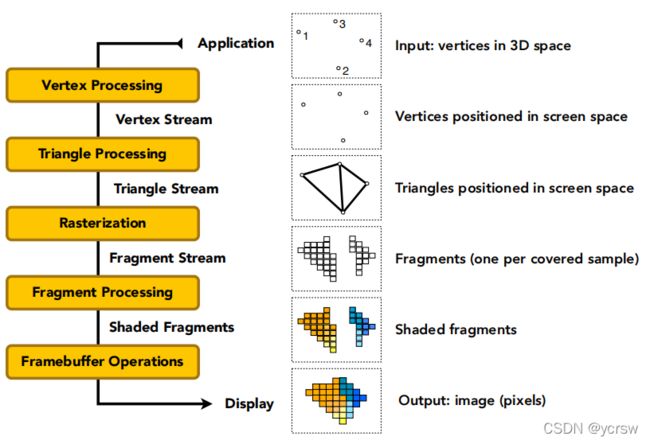
如上图所示,一般渲染管线分为这么几个部分:顶点处理、三角形处理、光栅化、片元处理、帧缓冲处理,整个流程完成了对图像的渲染,同样,本次作业的框架也是以来着这么一个渲染管线来进行图像的渲染。
6.1 输入处理
首先看到main.cpp文件,下面这段main函数的代码就是用来读取指定路径的模型文件,整合成三角形的集合作为渲染管线的输入(三角形是最基本的多边形)
std::vector<Triangle*> TriangleList;
std::string filename = "output.png";
objl::Loader Loader;
std::string obj_path = "../models/spot/";
// Load .obj File
bool loadout = Loader.LoadFile("../models/spot/spot_triangulated_good.obj");
for(auto mesh:Loader.LoadedMeshes)
{
for(int i=0;i<mesh.Vertices.size();i+=3)
{
Triangle* t = new Triangle();
for(int j=0;j<3;j++)
{
t->setVertex(j,Vector4f(mesh.Vertices[i+j].Position.X,mesh.Vertices[i+j].Position.Y,mesh.Vertices[i+j].Position.Z,1.0));
t->setNormal(j,Vector3f(mesh.Vertices[i+j].Normal.X,mesh.Vertices[i+j].Normal.Y,mesh.Vertices[i+j].Normal.Z));
t->setTexCoord(j,Vector2f(mesh.Vertices[i+j].TextureCoordinate.X, mesh.Vertices[i+j].TextureCoordinate.Y));
}
TriangleList.push_back(t);
}
}
然后下面这一段代码就是定义了一个fragment_shader_payload,并从命令行获取要使用的着色器,这个payload包括了 Fragment Shader 可能用到的参数,以及要使用的shader类型,它的通用性保证了调用不同的shader时不用再重复写不同的代码
std::function<Eigen::Vector3f(fragment_shader_payload)> active_shader = phong_fragment_shader;//定义一个返回类型是Eigen::Vector3f,传入参数类型是fragment_shader_payload的函数变量是active_shader,它等于函数phong_fragment_shader
if (argc >= 2)
{
command_line = true;
filename = std::string(argv[1]);
if (argc == 3 && std::string(argv[2]) == "texture")
{
std::cout << "Rasterizing using the texture shader\n";
active_shader = texture_fragment_shader;
texture_path = "spot_texture.png";
r.set_texture(Texture(obj_path + texture_path));
}
else if (argc == 3 && std::string(argv[2]) == "normal")
{
std::cout << "Rasterizing using the normal shader\n";
active_shader = normal_fragment_shader;
}
else if (argc == 3 && std::string(argv[2]) == "phong")
{
std::cout << "Rasterizing using the phong shader\n";
active_shader = phong_fragment_shader;
}
else if (argc == 3 && std::string(argv[2]) == "bump")
{
std::cout << "Rasterizing using the bump shader\n";
active_shader = bump_fragment_shader;
}
else if (argc == 3 && std::string(argv[2]) == "displacement")
{
std::cout << "Rasterizing using the bump shader\n";
active_shader = displacement_fragment_shader;
}
}
r.set_fragment_shader(active_shader);//把着色器函数传入光栅器的fragment_shader变量,这样在rasterizer.cpp里就可以直接调用fragment_shader,而不用写五段代码调用五个着色器了
接下来就是通过draw函数传入数据进光栅器,正式开始渲染管线流程
if (command_line)
{
r.clear(rst::Buffers::Color | rst::Buffers::Depth);
r.set_model(get_model_matrix(angle));
r.set_view(get_view_matrix(eye_pos));
r.set_projection(get_projection_matrix(45.0, 1, 0.1, 50));
r.draw(TriangleList);
...
6.2 顶点、三角形处理
接下来转向rasterizer.cpp,看到它的draw函数,这部分是对每个传入的三角形的顶点做处理(mvp坐标转换,设定顶点颜色和法向量),需要注意的是这部分代码多出了一段viewspace_pos变量的计算,从代码中看来,传入payload的三个顶点的坐标viewspace_pos是只经过MV变换,没有经过P投影变换的顶点坐标,说明shader里面默认都是在相机坐标系而不是世界坐标系下计算的。
还有一段对法向量的转换,是MV的逆矩阵的转置乘以各点的法向量,这段处理是因为原本顶点的法向量同样经过MVP转换后得到的并不是该点的法向量,如下图:
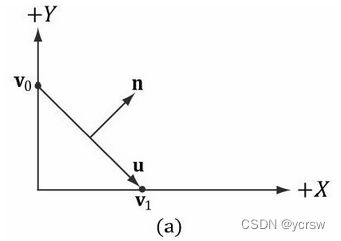
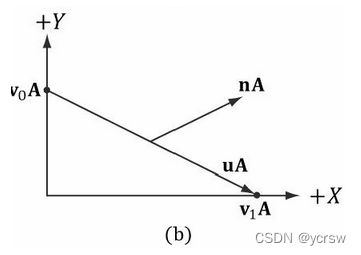
我们可以经过下述推导得到顶点转换后正确的法向量求法(设MVP为A):
根据法向量定义可得:
① n T ∗ u = 0. n^T*u=0. nT∗u=0.
② n ′ T ∗ ( A ∗ u ) = 0 n'^T*(A*u)=0 n′T∗(A∗u)=0
由①可得:
③ n T ∗ A − 1 ∗ A ∗ u = 0 n^T*A^{-1}*A*u=0 nT∗A−1∗A∗u=0
由③可得:
④ ( ( A − 1 ) T ∗ n ) T ∗ A ∗ u = 0 ((A^{-1})^T*n)^T*A*u=0 ((A−1)T∗n)T∗A∗u=0
由②和④可得:
n ′ = ( A − 1 ) T ∗ n n'=(A^{-1})^T*n n′=(A−1)T∗n
这样就能够得到正确的法向量结果了:
void rst::rasterizer::draw(std::vector<Triangle *> &TriangleList) {
float f1 = (50 - 0.1) / 2.0;
float f2 = (50 + 0.1) / 2.0;
Eigen::Matrix4f mvp = projection * view * model;
for (const auto& t:TriangleList)
{
Triangle newtri = *t;
std::array<Eigen::Vector4f, 3> mm {
(view * model * t->v[0]),
(view * model * t->v[1]),
(view * model * t->v[2])
};
std::array<Eigen::Vector3f, 3> viewspace_pos;
std::transform(mm.begin(), mm.end(), viewspace_pos.begin(), [](auto& v) {
return v.template head<3>();
});
Eigen::Vector4f v[] = {
mvp * t->v[0],
mvp * t->v[1],
mvp * t->v[2]
};
//Homogeneous division
for (auto& vec : v) {
vec.x()/=vec.w();
vec.y()/=vec.w();
vec.z()/=vec.w();
}
Eigen::Matrix4f inv_trans = (view * model).inverse().transpose();
Eigen::Vector4f n[] = {
inv_trans * to_vec4(t->normal[0], 0.0f),
inv_trans * to_vec4(t->normal[1], 0.0f),
inv_trans * to_vec4(t->normal[2], 0.0f)
};
//Viewport transformation
for (auto & vert : v)
{
vert.x() = 0.5*width*(vert.x()+1.0);
vert.y() = 0.5*height*(vert.y()+1.0);
vert.z() = vert.z() * f1 + f2;
}
for (int i = 0; i < 3; ++i)
{
//screen space coordinates
newtri.setVertex(i, v[i]);
}
for (int i = 0; i < 3; ++i)
{
//view space normal
newtri.setNormal(i, n[i].head<3>());
}
newtri.setColor(0, 148,121.0,92.0);
newtri.setColor(1, 148,121.0,92.0);
newtri.setColor(2, 148,121.0,92.0);
// Also pass view space vertice position
rasterize_triangle(newtri, viewspace_pos);
}
}
6.3 光栅化、片元处理、帧缓冲处理
这部分就是把点显示在屏幕上,涉及到深度Z-buffer的计算来判断点是否被遮挡,还涉及到顶点的shading计算,并把结果存入framebuffer中等待被调用,在rasterize_triangle函数中完成了这三部分的计算:
void rst::rasterizer::rasterize_triangle(const Triangle& t, const std::array<Eigen::Vector3f, 3>& view_pos)
{
auto v = t.toVector4();
Vector3f color;
float alpha, beta, gamma, lmin=INT_MAX, rmax=INT_MIN, tmax=INT_MIN, bmin=INT_MAX, id;
for(auto &k:v){//找到bounding box的边界坐标
lmin = int(std::min(lmin,k.x()));
rmax = std::max(rmax,k.x());rmax = rmax == int(rmax) ? int(rmax)-1 : rmax;
tmax = std::max(tmax,k.y());tmax = tmax == int(tmax) ? int(tmax)-1 : tmax;
bmin = int(std::min(bmin,k.y()));
}
for(float i = lmin; i <= rmax; i++){
for(float j = bmin; j <= tmax; j++){//遍历bounding box像素
id = get_index(i,j);
if(insideTriangle(i+0.5, j+0.5, t.v)){//如果像素在三角形内
// If so, use the following code to get the interpolated z value.
std::tie(alpha, beta, gamma) = computeBarycentric2D(i+0.5, j+0.5, t.v);
float w_reciprocal = 1.0/(alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
z_interpolated *= w_reciprocal;
if (-z_interpolated < depth_buf[id]){//如果该像素的深度更小,更新像素深度、颜色表
auto interpolated_color = interpolate(alpha, beta, gamma, t.color[0], t.color[1], t.color[2], 1);
auto interpolated_normal = interpolate(alpha, beta, gamma, t.normal[0], t.normal[1], t.normal[2], 1).normalized();
auto interpolated_texcoords = interpolate(alpha, beta, gamma, t.tex_coords[0], t.tex_coords[1], t.tex_coords[2], 1);
auto interpolated_shadingcoords = interpolate(alpha, beta, gamma, view_pos[0], view_pos[1], view_pos[2], 1);
fragment_shader_payload payload(interpolated_color, interpolated_normal.normalized(), interpolated_texcoords, texture ? &*texture : nullptr);
payload.view_pos = interpolated_shadingcoords;
depth_buf[id] = -z_interpolated;
frame_buf[id] = fragment_shader(payload);//payload作为参数传入着色器计算颜色
// TODO : set the current pixel (use the set_pixel function) to the color of the triangle (use getColor function) if it should be painted.
set_pixel({i,j}, frame_buf[id]);
}
}
}
}
}
6.4 显示
光栅器把所有点计算完后,回到main函数,利用opencv自带的方法从frame_buffer中取出计算好的数据画在图中并存储,自此,渲染管线的流程结束
...
r.draw(TriangleList);
cv::Mat image(700, 700, CV_32FC3, r.frame_buffer().data());
image.convertTo(image, CV_8UC3, 1.0f);
cv::cvtColor(image, image, cv::COLOR_RGB2BGR);
cv::imwrite(filename, image);
return 0;
}
7. 附件
附上源代码,有兴趣的朋友可以自己尝试一下效果:
CSDN:【GAMES101】作业3(提高)
GITHUB:【GAMES101】作业合集