分类任务评估2——推导ROC曲线、P-R曲线和K-S曲线

一.背景介绍

1.1数据来源

本文数据基于XGBoost模型调参、训练、评估、保存和预测的结果数据。真实结果及预测结果、预测为1的概率如下：

y_test = [1, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0]
y_pred = [0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0]
y_pred_proba = [0.2704021632671356, 0.0351046547293663, 0.8921366333961487, 0.046649616211652756, 0.17434531450271606,
                0.21389029920101166, 0.6692600846290588, 0.8160045742988586, 0.8550902605056763, 0.9786821007728577,
                0.9571514129638672, 0.10502149909734726, 0.5201050043106079, 0.032392870634794235]

1.2评估指标的粗浅解释

正式开始前需要提前掌握的内容，如已掌握可跳过直接看推导：
分类任务评估1——推导sklearn分类任务评估指标：混淆矩阵、查准率、查全率、假报警率计算；通过sklearn复现ROC曲线、AUC值，即《ROC曲线和AUC值的粗浅解释》章节

1.3本文推导的前提

只借助3个最基础的工具包，不使用任何sklearn的模块

import pandas as pd
import matplotlib.pyplot as plt
import warnings

warnings.filterwarnings('ignore')
plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei']

二.结论先行

完整脚本在第三部分，这里先来写结论

2.1结果展示

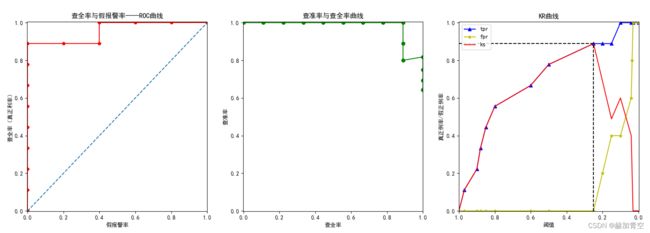
2.1.1ROC曲线、P-R曲线和K-S曲线绘制

2.1.2不同阈值下基础指标

不同阈值下 查全率 tpr: [0.0, 0.1111111111111111, 0.2222222222222222, 0.3333333333333333, 0.4444444444444444, 0.5555555555555556, 0.6666666666666666, 0.7777777777777778, 0.8888888888888888, 0.8888888888888888, 0.8888888888888888, 1.0, 1.0, 1.0, 1.0, 1.0]
不同阈值下 假报警率 fpr: [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.2, 0.4, 0.4, 0.6, 0.8, 1.0, 1.0]
不同阈值下 查准率 precisions: [1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 0.8888888888888888, 0.8, 0.8181818181818182, 0.75, 0.6923076923076923, 0.6428571428571429, 0.6428571428571429]
不同阈值下 真阳性 tp: [0, 1, 2, 3, 4, 5, 6, 7, 8, 8, 8, 9, 9, 9, 9, 9]
不同阈值下 假阳性 fp: [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 2, 2, 3, 4, 5, 5]
不同阈值下 假阴性 fn: [9, 8, 7, 6, 5, 4, 3, 2, 1, 1, 1, 0, 0, 0, 0, 0]

2.2结论总结

2.2.1一切源于阈值的变化

1.不同阈值下，根据预测概率会得出一系列混淆矩阵，因此会有一系列的查全率、查准率、假报警率；

# 阈值根据自己的预测概率结果，自行调整。数据越多，划分越细，就越接近于曲线
# 因为数值较少，按照下面阈值的设置，每次都会多1个被预测为真，即TP+FP每次增加1个
thresholds_self = [1, 0.97, 0.9, 0.88, 0.85, 0.8, 0.6, 0.5, 0.25, 0.2, 0.15, 0.1, 0.04, 0.035, 0.03, 0]

# 预测结果如 2.2.2不同阈值下基础指标 不再赘述

2.不同阈值下的查全率和假报警率构成ROC曲线；
3.不同阈值下的查准率和查全率构成查准率-查全率曲线；
4.参与预测的样本越多，阈值可划分的就更详细，得到的一系列指标也就更多，线的绘制就越接近于曲线。

2.2.2ROC曲线的结论

1.任何分类任务的目标都是追求高查全率（TPR）和低假报警率（FPR）；

# 查全率/召回率
Recall = TP / (TP + FN)
print('Recall: %.2f%%' % (Recall * 100))

# 假报警率
FPR = FP / (FP + TN)
print('FPR: %.2f%%' % (FPR * 100))

2.在既定的测试结果概率下，阈值由大到小排列，随着阈值的缩小，TPR增大时，FPR不变或提升；
3.曲线下面积AUC越大越好，最小值为蓝色虚线下面积0.5，值的变化范围在蓝色虚线和红色实线围成的面积0-0.5之间。

2.2.3查全率-查准率曲线的结论

1.查准率不包含任何假阴性样本（FN）的信息，查全率不包含任何假阳性样本（FP）的信息，两者均不能完整评估学习性能，且相互补充。

# 精准率
Precision = TP / (TP + FP)
print('Precision: %.2f%%' % (Precision * 100))

# 查全率/召回率
Recall = TP / (TP + FN)
print('Recall: %.2f%%' % (Recall * 100))

2.任何分类任务的目标都是追求高查全率和高查准率，但由查准率-查全率曲线和查准率precisions和查全率 tpr数值可以发现，高查全率和高查准率这两个目标是冲突的。原因在于在既定的测试结果概率下，随着阈值的缩小，越来越多的样本被判断为真，随着TP增加，FP也增加（FP也可能不变，但不影响整体趋势）。

不同阈值下 真阳性 tp: [0, 1, 2, 3, 4, 5, 6, 7, 8, 8, 8, 9, 9, 9, 9, 9]
不同阈值下 假阳性 fp: [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 2, 2, 3, 4, 5, 5]
不同阈值下 假阴性 fn: [9, 8, 7, 6, 5, 4, 3, 2, 1, 1, 1, 0, 0, 0, 0, 0]

3.作为查全率和查准率的折中，F值定义为查全率和查准率的调和平均数。F1便是其中一个调和平均数，是查准率和查全率同等重要的情况。
特殊情况说明：本例中出现，查全率上升、查准率也上升的情况（precision=0.8，recall=tpr=0.8888）——>（precision=0.81818，recall=tpr=1.0），查数可知：threshold_self=0.15到threshold_self=0.1时，TP增加，FP不变，所以precision有提升，但随着阈值缩小并没有影响随着查全率上升、查准率下降的整体趋势。

阈值threshold_self=0.2时，precision=TP/(TP+FP)=8/(8+1)=0.8888，recall=TP/(TP+FN)=8/(8+1)=0.8888

阈值threshold_self=0.15时，precision=TP/(TP+FP)=8/(8+2)=0.8，recall=TP/(TP+FN)=8/(8+1)=0.8888

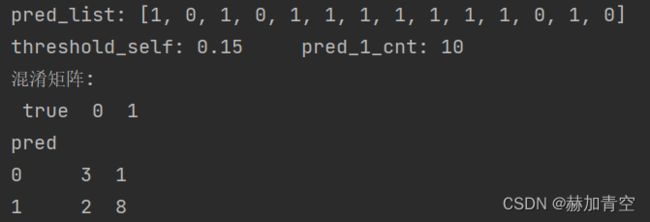
阈值threshold_self=0.1时，precision=TP/(TP+FP)=9/(9+2)=0.8181，recall=TP/(TP+FN)=9/(9+0)=1

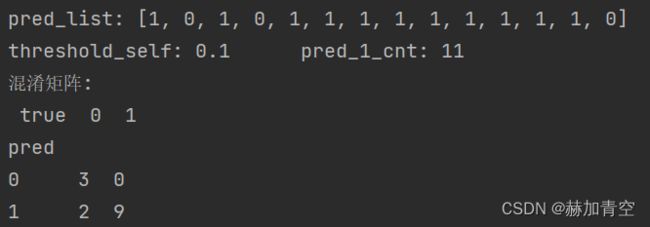
2.2.4K-S曲线的结论

1.K-S曲线绘制的丑是丑了点，但不影响结论，当参与的样本足够多时，自然会是3条平滑曲线，如下图（百度图片）。

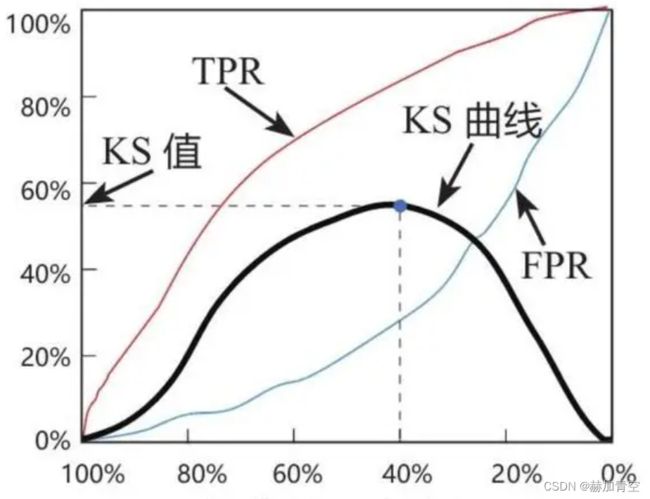
2.K-S曲线的横轴阈值是预测为正的概率阈值，由高到低降序排列，从1到0不能反，反了就彻底错了。
3.由2.1.1中绘制的K-S曲线图可以看出，阈值为0.25时(thresholds_self[ks.index(max(ks))])，KS曲线获得最大值0.888(max(ks))。在预测为正的概率阈值=0.25时，模型将好坏样本最分得开，区分如下图，阈值0.5时，2个样本区分错误，阈值0.25时仅1个样本区分错误。所以可以得出结论，KS值反应的是模型对类别区分的最大能力。

4.KS曲线与ROC曲线使用的都是tpr和fpr绘制，KS值是KS曲线的最大值max(abs(fpr - tpr))，AUC值是ROC曲线下面积。两个曲线对应的值都可以用来评估模型的好坏，具体使用没有绝对区分，可以和准确率一起综合来判断模型好坏。

三.计算和曲线绘制

3.1计算推导脚本

import pandas as pd
import matplotlib.pyplot as plt
import warnings

warnings.filterwarnings('ignore')
plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei']

# 数据
y_test = [1, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0]
y_pred = [0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0]
y_pred_proba = [0.2704021632671356, 0.0351046547293663, 0.8921366333961487, 0.046649616211652756, 0.17434531450271606,
                0.21389029920101166, 0.6692600846290588, 0.8160045742988586, 0.8550902605056763, 0.9786821007728577,
                0.9571514129638672, 0.10502149909734726, 0.5201050043106079, 0.032392870634794235]

# 空列表准备
fpr = []
tpr = []
precisions = []
tp = []
fp = []
fn = []

# 阈值准备
thresholds_self = [1, 0.97, 0.9, 0.88, 0.85, 0.8, 0.6, 0.5, 0.25, 0.2, 0.15, 0.1, 0.04, 0.035, 0.03, 0]
# 不同阈值的FPR\TPR\查准率生成
for threshold_self in thresholds_self:
    # 当前阈值下的预测结果
    pred = [1 if i >= threshold_self else 0 for i in y_pred_proba]
    print('pred_list:', pred)
    # print('threshold_self:', threshold_self, '\t', 'pred_1_cnt:', sum(pred))

    # 生成混淆矩阵
    feature_data = [pred, y_test]
    df = pd.DataFrame(feature_data).T.reset_index().rename(columns={0: 'pred', 1: 'true'})
    ptl = pd.pivot_table(df, values='index', index='pred', columns='true', aggfunc='count', fill_value=0)
    # 全部预测为真，或全部预测为假时，混淆矩阵的补充
    if ptl.shape[0] == 1:
        if ptl.index == 0:
            ptl.loc[1] = [0, 0]
        elif ptl.index == 1:
            ptl.loc[0] = [0, 0]
            ptl = ptl.sort_index()
    print('混淆矩阵:', '\n', ptl)

    # 从混淆矩阵提取基础值
    TP = ptl.iat[1, 1]
    FN = ptl.iat[0, 1]
    FP = ptl.iat[1, 0]
    TN = ptl.iat[0, 0]

    # 单一指标计算
    FPR = FP / (FP + TN)
    TPR = TP / (TP + FN)
    precision = TP / (TP + FP)

    # 不同阈值下的计算数据收集
    fpr.append(FPR)
    tpr.append(TPR)
    tp.append(TP)
    fp.append(FP)
    fn.append(FN)
    precisions.append(precision)

# 查准率空值特殊处理，替换为1；也可以删除，绘制查全率-查准率曲线时，同时删除相应位置查全率值即可
precisions = [i if i > -0.1 else 1.0 for i in precisions]
ks = [m - n for m, n in zip(tpr, fpr)]

print('不同阈值下 查全率 tpr:', tpr)
print('不同阈值下 假报警率 fpr:', fpr)
print('不同阈值下 查准率 precisions:', precisions)
print('不同阈值下 真阳性 tp:', tp)
print('不同阈值下 假阳性 fp:', fp)
print('不同阈值下 假阴性 fn:', fn)

3.2绘制三个曲线

# 直接接上面的代码即可直接运行
# ROC曲线
plt.figure(figsize=(24, 6))
plt.subplot(131)
plt.plot(fpr, tpr, marker='p', color='r')
plt.plot([0, 1], [0, 1], '--')
plt.xlim([-0.002, 1])
plt.ylim([-0.002, 1.005])
plt.xlabel('假报警率')
plt.ylabel('查全率（真正利率）')
plt.title('查全率与假报警率——ROC曲线')

# 查全率-查准率曲线
plt.subplot(132)
plt.plot(tpr, precisions, marker='o', color='g')
plt.xlim([-0.002, 1])
plt.ylim([-0.002, 1.005])
plt.xlabel('查全率')
plt.ylabel('查准率')
plt.title('查准率与查全率曲线')

# KS曲线
plt.subplot(133)
plt.plot(thresholds_self, tpr, marker='^', color='b', label='tpr')
plt.plot(thresholds_self, fpr, marker='*', color='y', label='fpr')
plt.plot(thresholds_self, [m - n for m, n in zip(tpr, fpr)], marker='', color='r', label='ks')
plt.axvline(x=thresholds_self[ks.index(max(ks))], ymax=max(ks), color='k', linestyle='--')
plt.axhline(y=max(ks), xmax=1-thresholds_self[ks.index(max(ks))], color='k', linestyle='--')
plt.xlim([1, -0.002])
plt.ylim([-0.002, 1.005])
plt.xlabel('阈值')
plt.ylabel('真正例率/假正例率')
plt.title('KR曲线')
plt.legend(loc="upper left")
plt.show()

---

声明：本文所载信息不保证准确性和完整性。文中所述内容和意见仅供参考，不构成实际商业建议，可收藏可转发但请勿转载，如有雷同纯属巧合。